Известия РАН. Серия физическая, 2022, T. 86, № 1, стр. 122-127

ВВЕДЕНИЕ

Пусть имеется некоторый объект (так называемый рассеиватель), который локализован в ограниченной области $\Re $ и характеризуется скоростью звука $c{\text{(}}\vec {r}{\text{)}}$ и амплитудным коэффициентом поглощения $\alpha (\vec {r},\omega )$ на частоте $\omega .$ Фоновая среда, т.е. среда вне области рассеяния $\Re ,$ предполагается однородной, изотропной, непоглощающей; она характеризуется постоянными значениями скорости звука ${{c}_{0}}$ и плотности ${{\rho }_{0}}.$ В рассматриваемом объекте плотность ${{\rho }_{0}}$ полагается той же. Упомянутые характеристики объекта, т.е. пространственные распределения $c{\text{(}}\vec {r}{\text{)}}$ и $\alpha (\vec {r},\omega ),$ неизвестны и подлежат определению. С этой целью исследуемый объект в акустическом томографическом эксперименте зондируется падающим полем $G_{0}^{{cl}}(\vec {y},\vec {x};{{\omega }}).$ Здесь верхний символ “cl” означает, что рассматриваются классические поля, в отличие от обобщенных полей, которые применяются при решении обратной задачи в ряде функционально-аналитических алгоритмов [1–5]. Радиус-векторы $\vec {x}$ и $\vec {y},$ характеризующие, соответственно, положение излучателя и положение приемника, находятся, по постановке задачи, вне области рассеяния $\Re {\text{:}}$ $\vec {x},\vec {y} \notin \Re .$ Падающее поле $G_{0}^{{cl}}(\vec {y},\vec {x};{{\omega }}),$ достигая объекта, рассеивается на нем, и в результате создается полное поле ${{G}^{{cl}}}(\vec {y},\vec {x};{{\omega }}).$ Поля ${{G}^{{cl}}}(\vec {y},\vec {x};{{\omega }})$ регистрируются в области приема $\Upsilon $ при каждом фиксированном излучателе $\vec {x}{\text{:}}$ $\vec {y} \in \Upsilon .$ После этого рассматривается и фиксируется новый излучатель, находящийся в области χ ($\vec {x} \in \chi $), т.е. задается новое падающее поле, и измерения повторяются. В результате получается набор экспериментальных данных рассеяния – полей ${{G}^{{cl}}}(\vec {y},\vec {x};{{\omega }}),$ $\vec {x} \in \chi {\text{,}}$ $\vec {y} \in \Upsilon .$ Этот набор предназначается для восстановления искомых характеристик объекта-рассеивателя, который при волновом подходе описывается функцией

временная зависимость полей полагается в виде $\sim {\kern 1pt} \exp ( - i\omega t).$

АЛГОРИТМ КОРРЕКЦИИ

Рассматриваемая ниже проблема заключается в следующем. На практике данные рассеяния получаются с помощью антенной решетки, характеристики которой, в общем случае, отклоняются от идеальных. Например, в ультразвуковом медицинском томографе [6–9], предназначенном для диагностики мягких биотканей (в первую очередь, молочной железы), одним из видов неидеальностей являются смещения (так называемые геометрические поправки) приемоизлучающих преобразователей антенной решетки от их идеальных положений. Поскольку величина таких смещений может быть соизмерима с длиной волны, смещения должны учитываться на этапе обработки экспериментальных данных. Эта обработка осуществляется с целью получения томограмм исследуемого объекта – оценок искомых пространственных распределений $c{\text{(}}\vec {r}{\text{)}}$ и $\alpha (\vec {r},\omega ).$ В противном случае разрешающая способность томограмм будет резко ухудшаться, и мелкие детали с размером, соизмеримым с длиной волны и менее, не будут воспроизводиться. В то же время, в медицинских приложениях такие мелкие детали являются наиболее информативными для целей ранней диагностики патологий [10]. В связи с обозначенной проблемой, смещения приемоизлучающих преобразователей предварительно находятся специально разработанным алгоритмом [9, 11]. Ниже предлагается алгоритм коррекции данных рассеяния, который позволяет пересчитать (скорректировать) данные, полученные при уже известных смещенных положениях излучателей и приемников, в данные при идеальных положениях. Этот алгоритм будет изложен, для определенности, на примере двумерного пространства. Однако при рассмотрении трехмерного пространства логика и последовательность действий не изменяются.

Рассмотрим классические запаздывающие рассеянные поля: $G_{{sc}}^{{cl}}(\vec {y},\vec {x};{{\omega }}) \equiv {{G}^{{cl}}}(\vec {y},\vec {x};{{\omega }}) - $ $ - \,\,G_{0}^{{cl}}(\vec {y},\vec {x};{{\omega }}),$ $\vec {x} \in \chi {\text{,}}$ $\vec {y} \in \Upsilon {\text{;}}$ в полярной системе координат $\vec {x} = \left\{ {\left| {\vec {x}} \right|,\left. {{{\varphi }_{{\vec {x}}}}} \right\}} \right.,$ $\vec {y} = \left\{ {\left| {\vec {y}} \right|,\left. {{{\varphi }_{{\vec {y}}}}} \right\}} \right..$ При $\vec {y} \notin \Re $ и каждом фиксированном $\vec {x}$ в двумерном случае имеет место разложение рассеянного поля по угловым гармоникам ${{q}_{{\vec {y}}}} = 0, \pm 1, \pm 2,...$ [12] (предполагается, что выбором начала координат внутри области $\Re $ обеспечивается условие $\left| {\vec {y}} \right| > \left| {\vec {r}} \right|,$ $\forall \vec {r} \in \Re $):

Здесь $H_{{{{q}_{{}}}}}^{{(1)}}$ – функция Ханкеля 1-го рода $q$-го порядка; ${{k}_{{\text{0}}}} = {\omega \mathord{\left/ {\vphantom {\omega {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$ – волновое число фоновой среды. В свою очередь, коэффициенты разложения $a{}_{{{{q}_{{\vec {y}}}}}}(\vec {x}, {{\omega }})$ выражаются через так называемые вторичные источники ${{I}^{{cl}}}(\vec {r},\vec {x};{{\omega }}),$ которые порождают рассеянное поле $G_{{sc}}^{{cl}}$ [12]:

где ${{J}_{q}}$ – функция Бесселя $q$-го порядка; $\vec {r} = \left\{ {\left| {\vec {r}} \right|,\left. {{{\varphi }_{{\vec {r}}}}} \right\}} \right.,$ $d\vec {r} = \left| {\vec {r}} \right| \cdot d\left| {\vec {r}} \right| \cdot d{{\varphi }_{{\vec {r}}}}$ в рассматриваемом двумерном пространстве.

Выражение типа (2) имеет место и для полных полей [12], однако исходно в (2) удобно рассматривать, для дальнейших целей, именно рассеянные поля. Дело в том, что вторичные источники ${{I}^{{cl}}}(\vec {r},\vec {x};{{\omega }})$ сами выражаются через полное поле ${{G}^{{cl}}},$ согласно (3). Это позволяет получить еще одно разложение, теперь уже для $a{}_{{{{q}_{{\vec {y}}}}}}(\vec {x}, {{\omega }}),$ и потом преобразовать (2). А именно, поскольку в (4) $\vec {r} \in \Re ,$ и при этом $\vec {x} \notin \Re $ по постановке задачи, то для полного поля ${{G}^{{cl}}}(\vec {r},\vec {x};{{\omega }})$ справедливо представление [12]:

${{q}_{{\vec {x}}}} = 0, \pm 1, \pm 2,...;$ $C{}_{{{{q}_{{\vec {x}}}}}}(\vec {r}, {{\omega }})$ – некоторые коэффициенты. Подстановка (3) и (5) в (4) дает:

где ${{b}_{{{{q}_{{\vec {y}}}}{{q}_{{\vec {x}}}}}}}({{\omega }})$ ≡ $ - \frac{i}{4}\int_\Re {{{J}_{{{{q}_{{\vec {y}}}}}}}} ({{k}_{{\text{0}}}}\left| {\vec {r}} \right|){\text{ exp(}} - i{{q}_{{\vec {y}}}}{{\varphi }_{{\vec {r}}}})$ × × $\nu (\vec {r},{{\omega }})C{}_{{{{q}_{{\vec {x}}}}}}(\vec {r}, {{\omega }})d\vec {r}$ – коэффициенты разложения. Подстановка (6) в (2) приводит к итоговому выражению

Надо еще раз обратить внимание, что для правомерности соотношения (7) необходимо только обеспечить условие $\left| {\vec {y}} \right| > \left| {\vec {r}} \right|,$ $\left| {\vec {x}} \right| > \left| {\vec {r}} \right|,$ $\forall \vec {r} \in \Re ,$ что достигается соответствующим выбором начала координат внутри области $\Re .$ С физической точки зрения, выражение (7) представляет собой разложение рассеянного поля по двойным угловым гармоникам ${{b}_{{{{q}_{{\vec {y}}}}{{q}_{{\vec {x}}}}}}}({{\omega }})H_{{{{q}_{{\vec {x}}}}}}^{{(1)}}({{k}_{{\text{0}}}}\left| {\vec {x}} \right|){\text{ }}H_{{{{q}_{{\vec {y}}}}}}^{{(1)}}({{k}_{{\text{0}}}}\left| {\vec {y}} \right|),$ где ${{q}_{{\vec {x}}}},$ ${{q}_{{\vec {y}}}} = 0, \pm 1, \pm 2,...$

Таким образом, согласно (7), знание коэффициентов ${{b}_{{{{q}_{{\vec {y}}}}{{q}_{{\vec {x}}}}}}}({{\omega }})$ позволяет найти рассеянные поля $G_{{sc}}^{{cl}}(\vec {y},\vec {x};{{\omega }})$ для произвольных точек вне области рассеяния $\vec {x}, \vec {y} \notin \Re .$ Это обстоятельство позволяет ниже предложить алгоритм пересчета (коррекции) полей, измеренных при определенных положениях излучателей и приемников, в поля при других положениях излучателей и приемников.

Пусть из эксперимента известны поля $G_{{sc}}^{{cl}}$$(\vec {y} = {{\vec {y}}^{{ex}}},\vec {x} = {{\vec {x}}^{{ex}}};{{\omega }}),$ измеренные для дискретных наборов положений излучателей $\left\{ {{{{\vec {x}}}^{{ex}}}} \right\}$ и приемников $\left\{ {{{{\vec {y}}}^{{ex}}}} \right\},$ где ${{\vec {x}}^{{ex}}} = \left\{ {\left| {{{{\vec {x}}}^{{ex}}}} \right|,\left. {\varphi _{{\vec {x}}}^{{ex}}} \right\}} \right.,$ ${{\vec {y}}^{{{\text{ex}}}}} = \left\{ {\left| {{{{\vec {y}}}^{{{\text{ex}}}}}} \right|,\left. {\varphi _{{\vec {y}}}^{{ex}}} \right\}} \right.,$ ${{\vec {x}}^{{ex}}} \notin \Re ,$ ${{\vec {y}}^{{ex}}} \notin \Re .$ В общем случае, эти положения смещены относительно их идеальных положений. В случае, когда все излучатели и все приемники располагаются на идеальных окружностях с соответствующим радиусом $\left| {{{{\vec {x}}}^{{ex}}}} \right| \equiv {\text{const}}$ и $\left| {{{{\vec {y}}}^{{ex}}}} \right| \equiv {\text{const,}}$ коэффициенты ${{b}_{{{{q}_{{\vec {y}}}}{{q}_{{\vec {x}}}}}}}({{\omega }})$ находятся двойным фурье-преобразованием (по углам $\varphi _{{\vec {y}}}^{{ex}}$ и $\varphi _{{\vec {x}}}^{{ex}}$):

Это соотношение следует из вида выражения (7).

В более общем случае точки ${{\vec {x}}^{{ex}}} \in \chi $ и ${{\vec {y}}^{{ex}}} \in \Upsilon {\text{,}}$ для которых измеряются экспериментальные данные, лежат на некоторой “деформированной” окружности или даже на контурах произвольной формы. Тогда коэффициенты ${{b}_{{{{q}_{{\vec {y}}}}{{q}_{{\vec {x}}}}}}}({{\omega }})$ могут быть найдены решением линейной системы уравнений (7), получающейся перебором точек ${{\vec {x}}^{{ex}}}$ и ${{\vec {y}}^{{ex}}},$ для которых известны рассеянные поля $G_{{sc}}^{{cl}}({{\vec {y}}^{{ex}}},{{\vec {x}}^{{ex}}};{{\omega }}){\text{:}}$

Естественно, что общее количество и характер дискретизованных данных $G_{{sc}}^{{cl}}\left( {{{{\vec {y}}}^{{ex}}},{{{\vec {x}}}^{{ex}}};{{\omega }}} \right)$ должны обеспечивать единственность решения системы (8).

Однако с точки зрения размерности решаемых систем уравнений, удобнее сначала найти коэффициенты ${{\left\{ {{{a}_{{{{q}_{{\vec {y}}}}}}}\left( {{{{\vec {x}}}^{{ex}}}, {{\omega }}} \right)} \right\}}_{{{{q}_{{\vec {y}}}}}}}.$ Эти коэффициенты находятся из системы линейных уравнений (2), получающейся перебором точек $\vec {y} = {{\vec {y}}^{{ex}}}$ при каждом фиксированном $\vec {x} = {{\vec {x}}^{{ex}}}{\text{:}}$

Далее по уже известным значениям ${{a}_{{{{q}_{{\vec {y}}}}}}}\left( {{{{\vec {x}}}^{{ex}}}, {{\omega }}} \right)$ из системы линейных уравнений (6), получающейся перебором $\vec {x} = {{\vec {x}}^{{ex}}}$ и решаемой при каждом фиксированном ${{q}_{{\vec {y}}}},$ находятся коэффициенты ${{b}_{{{{q}_{{\vec {y}}}}{{q}_{{\vec {x}}}}}}}({{\omega }}){\text{:}}$

Наконец, уже известные коэффициенты ${{b}_{{{{q}_{{\vec {y}}}}{{q}_{{\vec {x}}}}}}}({{\omega }})$ позволяют опять использовать соотношение (7), однако теперь для вычисления полей $G_{{sc}}^{{cl}}(\vec {y},\vec {x};{{\omega }})$ при тех идеальных положениях преобразователей $\vec {x}$ и $\vec {y},$ которые будут использоваться на этапе восстановления характеристик исследуемого объекта. Например, входные данные для функционального алгоритма Новикова [1–3], строго учитывающего эффекты многократного рассеяния волн, в случае использования точечных приемоизлучающих преобразователей [4, 5] формируются для окружности радиуса ${{R}_{0}}{\text{:}}$ $\left| {\vec {x}} \right| = \left| {\vec {y}} \right| = {{R}_{0}}.$ Тогда (7) приобретает вид

где $\vec {x} = \left\{ {{{R}_{0}},\varphi _{{\vec {x}}}^{{\text{0}}}} \right\},$ $\vec {y} = \left\{ {{{R}_{0}},\varphi _{{\vec {y}}}^{{\text{0}}}} \right\}.$

Таким образом, в основе алгоритма коррекции данных рассеяния (8), (11) или же (9)–(11) лежит тот факт, что коэффициенты ${{b}_{{{{q}_{{\vec {y}}}}{{q}_{{\vec {x}}}}}}}({{\omega }})$ не зависят от конкретных значений точки излучения $\vec {x}$ и точки приема $\vec {y}$, которые находятся вне области рассеяния $\Re .$

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

Для иллюстрации работоспособности предложенного алгоритма коррекции данных рассеяния (9)–(11) был задан рефракционно-поглощающий рассеиватель $\nu (\vec {r},\omega ).$ Согласно (1), действительная часть функции рассеивателя (рис. 1а) формируется за счет неоднородностей скорости звука, а мнимая часть (рис. 1б) – за счет поглощения. Для определенности при моделировании задавались параметры, близкие к используемым в томографической установке [6–9]: характерная частота 1.25 МГц, c₀ = 1500 м/с; следовательно, длина волны в фоновой среде λ₀ = 1.2 × × 10^–3 м. Количество приемоизлучающих преобразователей (каждый из которых выступал как в роли излучателя, так и в роли приемника) было 128; преобразователи располагались на окружности радиуса 0.1536 м.

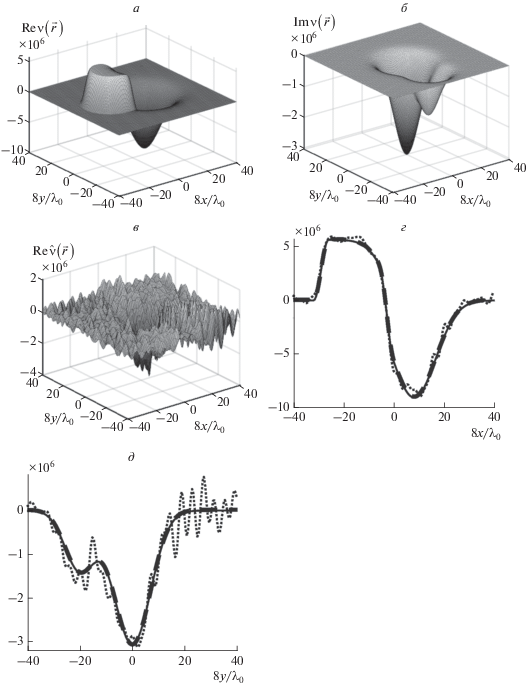
Волна, распространяясь вдоль некоторой траектории ${{l}_{\Re }},$ приобретает дополнительный набег фазы $\Delta \psi = \omega \int_{{{l}_{\Re }}} {\left[ {\frac{1}{{{{c}_{0}}}} - \frac{1}{{c(\vec {r})}}} \right]} d{{l}_{{\vec {r}}}}$ = $\frac{\omega }{{{{c}_{0}}}}\int_{{{l}_{\Re }}} {\frac{{\Delta c(\vec {r})}}{{c(\vec {r})}}} d{{l}_{{\vec {r}}}},$ где $\Delta c(\vec {r}) \equiv c(\vec {r}) - {{c}_{0}},$ $d{{l}_{{\vec {r}}}}$ – длина элемента траектории в окрестности точки $\vec {r}$. Так, наибольшие значения $\left| {\Delta \psi } \right|$ получаются при прохождении волны через центральное сечение рассеивателя вдоль оси $OX,$ где относительный контраст фазовой скорости ${{\Delta c(\vec {r})} \mathord{\left/ {\vphantom {{\Delta c(\vec {r})} {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$ изменяется от $ - 0.13$ до $0.12$ (рис. 1а, 1г). При этом дополнительный набег фазы составляет $\Delta \psi \approx - 0.72\,\pi $ на участке этого сечения с отрицательным контрастом скорости $\Delta c(\vec {r}) < 0,$ где $\operatorname{Re} \nu (\vec {r},\omega {\text{)}} < {\text{0;}}$ набег $\Delta \psi \approx 0.59\,\pi $ приобретается на участке с положительным контрастом скорости $\Delta c(\vec {r}) > 0,$ где $\operatorname{Re} \nu (\vec {r},\omega {\text{)}} > {\text{0}}{\text{.}}$ В то же время наибольшее суммарное поглощение достигается на центральном сечении рассеивателя вдоль оси $OY$ (рис. 1б, 1д), что приводит к затуханию амплитуды волны в $\exp \left[ {\int_{{{l}_{\Re }}} {\alpha (\vec {r})} d{{l}_{{\vec {r}}}}} \right] \approx 2.8$ раза. Тем самым, эффекты многократного рассеяния существенны. Для получения оценки $\hat {\nu }(\vec {r},\omega )$ рассеивателя $\nu (\vec {r},\omega )$ с учетом этих эффектов использовался функциональный алгоритм [1–5].

При моделировании квазиэкспериментальных данных – принимаемых рассеянных полей – учитывалось, что в томографической установке [6–9] каждый преобразователь антенной решетки выступает как в роли излучателя, так и в роли приемника. Смещения приемоизлучающих преобразователей от их идеальных положений на окружности задавались случайным образом. При этом максимальное смещение вдоль радиуса составляло 1.0 ⋅ 10^–3 м ≈ 0.83λ₀, а максимальное смещение по углу достигало углового расстояния между соседними преобразователями ${{2\pi } \mathord{\left/ {\vphantom {{2\pi } {128}}} \right. \kern-0em} {128}}.$ Тогда данные рассеяния $G_{{sc}}^{{cl}}\left( {{{{\vec {y}}}^{{ex}}},{{{\vec {x}}}^{{ex}}};{{\omega }}} \right)$ оказываются из-за смещений столь сильно искаженными (по сравнению со случаем несмещенных преобразователей), что оценка рассеивателя $\hat {\nu }(\vec {r},\omega ),$ восстановленная в монохроматическом режиме по нескорректированным данным, полностью разваливается даже в отсутствие каких-либо иных помех (рис. 1в). Однако те же самые изначальные данные $G_{{sc}}^{{cl}}\left( {{{{\vec {y}}}^{{ex}}},{{{\vec {x}}}^{{ex}}};{{\omega }}} \right),$ но после применения коррекции (9)–(11), оказываются практически полностью совпадающими с данными при несмещенных преобразователях. Как следствие, результат восстановления $\hat {\nu }(\vec {r},\omega )$ в отсутствие помех практически полностью совпадает с истинными значениями $\nu (\vec {r},\omega )$ (рис. 1г, 1д).

Кроме того, процедура коррекции (9)–(11) обладает хорошей помехоустойчивостью. Так, в рассеянные поля $G_{{sc}}^{{cl}}({{\vec {y}}^{{ex}}},{{\vec {x}}^{{ex}}};{{\omega }})$ вносилась случайная нормально распределенная шумовая помеха $n(\vec {y},\vec {x};\omega )$ с нулевым средним и среднеквадратичным амплитудным отклонением ${{\sigma }_{{ns}}} = 0.02\bar {G}_{{sc}}^{{cl}}$ независимо для действительной части и мнимой части помехи. Среднеквадратичное значение данных рассеяния

рассчитывалось с учетом смещения преобразователей для области излучения χ, совпадающей в данной модели с областью приема $\Upsilon $. Входное амплитудное отношение “помеха/сигнал” составляло

Оценка рассеивателя $\hat {\nu }(\vec {r},\omega ),$ полученная по зашумленным данным $G_{{sc}}^{{cl}}\left( {{{{\vec {y}}}^{{ex}}},{{{\vec {x}}}^{{ex}}};{{\omega }}} \right),$ к которым применялся алгоритм коррекции положений преобразователей, получилась адекватной (рис. 1г, 1д).

ЗАКЛЮЧЕНИЕ

Помимо рассмотренных смещений преобразователей антенной решетки от их идеальных положений, в упоминавшемся выше томографе [6–9] имеются другие виды несовершенств [9, 11] – фазовые поправки для излучаемых и принимаемых сигналов, а также поправки на смещение центра вращения антенной решетки от ее геометрического центра, поправки на непроизвольное движение пациента во время съема данных рассеяния. Однако, по сути, перечисленные виды поправок могут быть учтены заданием эффективных смещений приемоизлучающих преобразователей при измерении экспериментальных данных [9].