1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 10, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 10, стр. 1513-1520

Динамическое деформационное старение объемно-центрированных кубических металлов по механизму типа Снука

Б. В. Петухов *

Федеральное государственное учреждение “Федеральный научно-исследовательский центр “Кристаллография и фотоника” Российской академии наук, Институт кристаллографии имени А.В. Шубникова Российской академии наук
Москва, Россия

* E-mail: petukhov@ns.crys.ras.ru

Поступила в редакцию 01.06.2022
После доработки 15.06.2022
Принята к публикации 22.06.2022

Полный текст (PDF)

Аннотация

Развита модель динамического взаимодействия дислокаций, отвечающих за пластичность кристаллов, с примесной подсистемой для материалов с высоким потенциальным рельефом кристаллической решетки (барьерами Пайерлса). Показано, что взаимодействие примесей с дислокациями на наномасштабах, соответствующих механизму Снука, вызывает неустойчивости движения дислокаций в определенном интервале скоростей и проявляется в аномалиях макроскопического предела текучести кристаллических материалов.

ВВЕДЕНИЕ

Кристаллические материалы с объемно-центрированной кубической (ОЦК) структурой широко исследуются в связи с возможными высокотемпературными приложениями. Влияние примесей на динамику дислокаций существенно модифицирует механические свойства кристаллов и является предметом всестороннего изучения, как экспериментального, так и теоретического [1–6]. Статичные примеси, “вмороженные” в кристаллическую решетку, могут как упрочнять, так и разупрочнять ОЦК металлы [6–8]. Приобретающие подвижность в определенном температурном интервале примеси диффундируют к дислокациям и осаждаются на них, модифицируя динамические характеристики дислокаций своим коллективным влиянием и приводя к их так называемому “старению”. На макроскопическом уровне это вызывает “деформационное старение” материала в целом. Возможна также индуцированная примесями трансформация структуры ядер дислокаций [9–11]. При сравнимых подвижностях дислокаций и примесей нередко возникает нестабильность пластического течения, проявляющаяся в виде скачков на деформационных кривых (эффект Портевена–Ле Шателье [12, 13]).

Анализ экспериментальных данных значительно усложняется в условиях динамического старения, так как движение дислокаций перестает быть простым термоактивируемым процессом. Поэтому для такого анализа следует развивать и привлекать более сложные модели, учитывающие возможные физические механизмы взаимодействия дислокационной и примесной подсистем материала.

К настоящему времени динамическое взаимодействие примесей с дислокациями хорошо изучено для материалов с гранецентрированной кубической (ГЦК) структурой кристаллической решетки [14, 15] и значительно меньше для кристаллов с ОЦК структурой, полупроводников, керамик и других материалов, в которых движение дислокаций контролируется высоким потенциальным рельефом кристаллической решетки, называемым также барьерами Пайерлса [16]. Закономерности динамического старения дислокаций, зависящие от механизма их движения, кардинально различны для двух указанных типов материалов. В материалах с ГЦК структурой кристаллический рельеф низок и дислокации движутся по мере преодоления барьеров, созданных “дислокациями леса” или какими-либо заметно отстоящими друг от друга локальными центрами. В материалах с высоким кристаллическим рельефом барьеры расположены на микроскопическом расстоянии, равном периоду решетки [16, 17] и кинетика вносимого движущимися дислокациями возмущения примесной подсистемы совершенно иная.

Ключевым вопросом теории динамического деформационного старения материалов является вариация содержания примесей на дислокационных линиях. Однако этот вопрос в имеющихся работах освещается упрощенно и нередко кинетический закон просто постулируется [18]. Однако для лучшего понимания явления было бы полезно не постулировать, а вывести кинетический закон из лежащих в основе физических механизмов. Развитие соответствующей теории и является целью настоящей работы.

Экспериментально изучают как статическое старение покоящихся дислокаций, так и динамическое старение дислокаций при их движении под действием прикладываемой нагрузки. И в том, и другом случае в основе лежат одинаковые механизмы. Дело в том, что движение дислокации на микроуровне происходит скачкообразно и состоит из двух стадий: сравнительно долгого пребывания на месте в одной из долин кристаллического рельефа и быстрого перемещения через барьер при флуктуационном приобретении достаточно большой энергии для образования пары кинков [16]. Во время ожидания скачка примеси притекают на покоящуюся дислокацию, так что фактически имеет место статическое старение, но его продолжительность не задается, а регулируется в среднем высотой барьеров, температурой и прикладываемой нагрузкой. В первой части настоящей работы будут изучаться закономерности статического старения дислокаций. Затем полученные результаты будут использованы для расчета кинетики сегрегации примесей в повторяющихся циклах при перемещении дислокаций на значительные расстояния через череду барьеров. В заключительной части будет рассчитываться влияние сегрегированных примесей на макроскопические свойства кристаллических материалов: упрочнение и температурные аномалии предела текучести при пластической деформации.

МОДЕЛЬ КОРОТКОДЕЙСТВУЮЩИХ ПРИМЕСЕЙ

Скачкообразное термически активируемое изменение положения дислокации между долинами периодической кристаллической решетки [2, 3, 16, 17] приводит к перераспределению примесной атмосферы на каждом шаге. Кинетика такого перераспределения зависит от устройства потенциального рельефа для миграции примесей в окрестности дислокационного ядра. В отличие от ситуации в ГЦК кристаллах, положения дислокации до и после одного элементарного скачка в ОЦК кристаллах мало отличаются, и поэтому значительная часть сбрасываемых при скачке примесей релаксирует к новому положению, возвращаясь на дислокацию.

Вдали от дислокации миграционный рельеф периодичен и время τ0 смещения примеси на период решетки a имеет невозмущенное значение. В окрестности ядра потенциальный рельеф искажен взаимодействием, так что имеется глубокий минимум, отвечающий наиболее энергетически выгодному расположению примеси относительно дислокации, отмечаемый в дальнейшем буквой d. Притяжение к этому положению понижает барьер E для перехода примеси в него и уменьшает время соответствующего термоактивируемого скачка τ = ${{\tau }_{ * }}$exp(E/kT) по сравнению с временем обратного перехода τ1 = ${{\tau }_{ * }}_{1}$exp(E1/kT) или временем миграции вдали от ядра τ0 = ${{\tau }_{ * }}_{0}$exp(E0/kT), так что τ $ \ll $ τ0, τ1. Здесь ${{\tau }_{ * }}$, ${{\tau }_{ * }}_{1}$, ${{\tau }_{ * }}_{0}$ – предэкспоненциальные множители, принимаемые постоянными. Существование пониженного барьера E для перехода примесей в ядро дислокации по сравнению с барьерами переходов E0 в объеме кристалла приводит к необходимости выделения процессов перераспределения примесей вокруг ядра в особый класс, именуемый снуковским [19], и требует отдельного рассмотрения. Ограниченное исследование данной проблемы было произведено в [20]. В настоящей работе развивается новый эффективный подход, позволяющий получить более полное решение проблемы.

Основное внимание будет уделено расчету заполнения состояния d, а прочие состояния в простейшем приближении будут считаться слабо возмущенными и трактоваться как некий резервуар с постоянной средней концентрацией c0. Исключение составляют смежные с d состояния в плоскости скольжения +, –, поскольку вследствие движения дислокации с возможным увлечением или отставанием примесей между этими состояниями происходит существенное перераспределение примесной концентрации. Так как считается, что дислокации движутся с достаточно большой скоростью V, время ta = a/V, проводимое в одной долине кристаллического рельефа, в рассматриваемой упрощенной модели меньше или сравнимо с временем миграции примесей, что делает необходимым дискретное описание в отличие от континуальной модели Коттрелла [14].

СТАТИЧЕСКОЕ СТАРЕНИЕ ДИСЛОКАЦИЙ ПРИ КОРОТКОМАСШТАБНОЙ МИГРАЦИИ ПРИМЕСЕЙ

Изучим эволюцию примесного содержания в ядре дислокации, характеризуемого концентрацией cd в расчете на один период решетки вдоль дислокационной линии. Считается, что дислокация покоится или совершает малоамплитудные тепловые колебания перед барьером в ожидании большой флуктуации, способной перевести ее в соседнюю долину кристаллического рельефа. Введем также обозначения c+ и c– для концентраций примесей в состояниях + и –. Запишем уравнения для перераспределения примесных концентраций между этими состояниями и объемом кристалла в течение времени ожидания перехода ta

(1)
$\frac{{d{{c}_{d}}}}{{dt}} = {{{{({{c}_{ + }} + {{c}_{ - }})(1--{{c}_{d}})} \mathord{\left/ {\vphantom {{({{c}_{ + }} + {{c}_{ - }})(1--{{c}_{d}})} {\tau --{{c}_{d}}(2--{{c}_{ + }}--{{c}_{ - }})}}} \right. \kern-0em} {\tau --{{c}_{d}}(2--{{c}_{ + }}--{{c}_{ - }})}}} \mathord{\left/ {\vphantom {{{{({{c}_{ + }} + {{c}_{ - }})(1--{{c}_{d}})} \mathord{\left/ {\vphantom {{({{c}_{ + }} + {{c}_{ - }})(1--{{c}_{d}})} {\tau --{{c}_{d}}(2--{{c}_{ + }}--{{c}_{ - }})}}} \right. \kern-0em} {\tau --{{c}_{d}}(2--{{c}_{ + }}--{{c}_{ - }})}}} {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}},$
(2)
$\frac{{d{{c}_{ \pm }}}}{{dt}} = {{{{{{{{--{{c}_{ \pm }}(1--{{c}_{d}})} \mathord{\left/ {\vphantom {{--{{c}_{ \pm }}(1--{{c}_{d}})} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} \right. \kern-0em} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} \mathord{\left/ {\vphantom {{{{--{{c}_{ \pm }}(1--{{c}_{d}})} \mathord{\left/ {\vphantom {{--{{c}_{ \pm }}(1--{{c}_{d}})} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} \right. \kern-0em} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} {{{\tau }_{1}}--{{c}_{ \pm }}(1--{{c}_{0}})}}} \right. \kern-0em} {{{\tau }_{1}}--{{c}_{ \pm }}(1--{{c}_{0}})}}} \mathord{\left/ {\vphantom {{{{{{--{{c}_{ \pm }}(1--{{c}_{d}})} \mathord{\left/ {\vphantom {{--{{c}_{ \pm }}(1--{{c}_{d}})} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} \right. \kern-0em} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} \mathord{\left/ {\vphantom {{{{--{{c}_{ \pm }}(1--{{c}_{d}})} \mathord{\left/ {\vphantom {{--{{c}_{ \pm }}(1--{{c}_{d}})} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} \right. \kern-0em} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} {{{\tau }_{1}}--{{c}_{ \pm }}(1--{{c}_{0}})}}} \right. \kern-0em} {{{\tau }_{1}}--{{c}_{ \pm }}(1--{{c}_{0}})}}} {{{\tau }_{0}} + {{c}_{0}}(1{\text{ }}--{{c}_{ \pm }})}}} \right. \kern-0em} {{{\tau }_{0}} + {{c}_{0}}(1{\text{ }}--{{c}_{ \pm }})}}} \mathord{\left/ {\vphantom {{{{{{{{--{{c}_{ \pm }}(1--{{c}_{d}})} \mathord{\left/ {\vphantom {{--{{c}_{ \pm }}(1--{{c}_{d}})} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} \right. \kern-0em} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} \mathord{\left/ {\vphantom {{{{--{{c}_{ \pm }}(1--{{c}_{d}})} \mathord{\left/ {\vphantom {{--{{c}_{ \pm }}(1--{{c}_{d}})} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} \right. \kern-0em} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} {{{\tau }_{1}}--{{c}_{ \pm }}(1--{{c}_{0}})}}} \right. \kern-0em} {{{\tau }_{1}}--{{c}_{ \pm }}(1--{{c}_{0}})}}} \mathord{\left/ {\vphantom {{{{{{--{{c}_{ \pm }}(1--{{c}_{d}})} \mathord{\left/ {\vphantom {{--{{c}_{ \pm }}(1--{{c}_{d}})} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} \right. \kern-0em} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} \mathord{\left/ {\vphantom {{{{--{{c}_{ \pm }}(1--{{c}_{d}})} \mathord{\left/ {\vphantom {{--{{c}_{ \pm }}(1--{{c}_{d}})} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} \right. \kern-0em} {\tau + {{c}_{d}}(1{\text{ }}--{{c}_{ \pm }})}}} {{{\tau }_{1}}--{{c}_{ \pm }}(1--{{c}_{0}})}}} \right. \kern-0em} {{{\tau }_{1}}--{{c}_{ \pm }}(1--{{c}_{0}})}}} {{{\tau }_{0}} + {{c}_{0}}(1{\text{ }}--{{c}_{ \pm }})}}} \right. \kern-0em} {{{\tau }_{0}} + {{c}_{0}}(1{\text{ }}--{{c}_{ \pm }})}}} {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}}.$

Первые слагаемые в правых частях уравнений описывают поток примесей из смежных состояний (+), (–) в ядро (d) в единицу времени, вторые слагаемые описывают обратный поток. Третье и четвертое слагаемые в правой части уравнения (2) описывают обмен примесями состояний +, – с объемом кристалла. В уравнениях (1), (2) принимается во внимание, что переходы возможны лишь в незанятые состояния, так что, например, частота переходов в состояние d пропорциональна вероятности 1 – cd того, что узел свободен, и т. д. Количество примыкающих и дислокационных состояний может разниться на некоторое координационное число порядка нескольких единиц, но это число можно учесть соответствующей перенормировкой концентраций примесей.

С целью изучить эволюцию полной концентрации примесей в атмосфере ct = cd + c сложим уравнения (1) и (2). Здесь c суммарная концентрация примесей в окружении дислокационного ядра c = c+ + c–. Система уравнений (1), (2) преобразуется к виду

(3)
$\frac{{d{{c}_{t}}}}{{dt}} = {{(2{{c}_{0}}--c)} \mathord{\left/ {\vphantom {{(2{{c}_{0}}--c)} {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}}.$
(4)
$\frac{{\tau dc}}{{dt}} = ~--{{a}_{{\text{s}}}}{{с}^{2}}--{{b}_{{\text{s}}}}с--{{c}_{{\text{s}}}},$
где as = 1 – τ/τ1; bs = 1 – ct + τ/τ0 + (2 + ct) τ/τ1; cs = = –2τ(c0/τ0 + ct/τ1). Выпишем также следующее из (2) уравнение для cm = c+ – c–

(5)
$\frac{{d{{c}_{m}}}}{{dt}} = ~--{{c}_{m}}[{1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau } + {1 \mathord{\left/ {\vphantom {1 {{{\tau }_{0}}--{{c}_{d}}(\tau --{1 \mathord{\left/ {\vphantom {1 {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}})}}} \right. \kern-0em} {{{\tau }_{0}}--{{c}_{d}}(\tau --{1 \mathord{\left/ {\vphantom {1 {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}})}}].$

Пример численного решения системы уравнений (3), (4), иллюстрирующий основные закономерности кинетики сегрегации примесей в окрестности дислокационного ядра, приведен на рис. 1. Отметим качественные черты приведенного решения, используемые далее для упрощения описания и получения аналитических оценок. Из-за большой разницы времен перехода примесей в ядро дислокации τ и в соседние узлы решетки τ1, τ0 эволюция примесного содержания происходит в две существенно отличающиеся по длительности стадии. В течение времени порядка τ происходит только самый быстрый процесс перехода примесей из ближайших состояний (±) в ядро (d) практически без участия более удаленных примесей. Это называется в [19] и здесь механизмом Снука. И лишь впоследствии за время, превышающее τ0, происходит обмен с примесями из резервуара по механизму Коттрелла и устанавливается равновесное содержание. Это двухстадийное поведение иллюстрируется на вставке к рис. 1а. Показанное на этом же рисунке численное решение уравнений (3), (4) отвечает первой – снуковской – стадии.

Рис. 1.

Кинетика сегрегации примесей в дислокационной атмосфере: (а) показывает рост со временем полной концентрации примесей в атмосфере; (б) показывает штриховой линией вариацию примесей в окружении дислокационного ядра. Сплошная линия представляет концентрацию примесей, получающуюся в результате адиабатического подстраивания к полной концентрации (см. текст). Значения параметров: c0 = 0.01; τ0/τ = 13; τ1/τ = 21. Начальные значения концентраций есть c+in = 0.01; c–in = 0.015; cdin = 0.01. На вставке к рисунку (а) схематически показана в произвольных единицах типичная кривая статического старения в ванадии, содержащим примеси кислорода [20].

При большом превышении времен τ0 и τ1 над τ полная концентрация примесей на дислокации и вокруг нее ct нарастает медленно, как это следует из уравнения (3) ввиду большой величины τ0 и наглядно видно на рис. 1а. Из рис. 1б видно, что резкое изменение концентрации c в примыкающих к ядру состояниях имеет место за короткое время τ $ \ll $ τ0. Предположим в соответствии с этим, что c, начав с некоторого начального значения cin, быстро подстраивается под текущее медленно изменяющееся ct и затем уже изменяется более плавно. Решаем уравнение (4) в таком адиабатическом приближении, считая ct постоянным

(6)
$\begin{gathered} c = ~({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{{a}_{s}})\left\{ {\left[ {{{b}_{s}} + {{{({{b}_{s}}^{2}--4{{a}_{s}}{{c}_{s}})}}^{{1/2}}}} \right]B{\text{exp}}\left[ {{{--{{{({{b}_{s}}^{2}--4{{a}_{s}}{{c}_{s}})}}^{{1/2}}}t} \mathord{\left/ {\vphantom {{--{{{({{b}_{s}}^{2}--4{{a}_{s}}{{c}_{s}})}}^{{1/2}}}t} \tau }} \right. \kern-0em} \tau }} \right] - } \right. \\ {{ - \,\,\,\left. {\left[ {{{b}_{s}} - {{{({{b}_{s}}^{2}--4{{a}_{s}}{{c}_{s}})}}^{{1/2}}}} \right]A} \right\}} \mathord{\left/ {\vphantom {{ - \,\,\,\left. {\left[ {{{b}_{s}} - {{{({{b}_{s}}^{2}--4{{a}_{s}}{{c}_{s}})}}^{{1/2}}}} \right]A} \right\}} {\left\{ {A--B{\text{exp}}[{{--{\text{ }}{{{({{b}_{s}}^{2}--4{{a}_{s}}{{c}_{s}})}}^{{1/2}}}t} \mathord{\left/ {\vphantom {{--{\text{ }}{{{({{b}_{s}}^{2}--4{{a}_{s}}{{c}_{s}})}}^{{1/2}}}t} \tau }} \right. \kern-0em} \tau }]} \right\}}}} \right. \kern-0em} {\left\{ {A--B{\text{exp}}[{{--{\text{ }}{{{({{b}_{s}}^{2}--4{{a}_{s}}{{c}_{s}})}}^{{1/2}}}t} \mathord{\left/ {\vphantom {{--{\text{ }}{{{({{b}_{s}}^{2}--4{{a}_{s}}{{c}_{s}})}}^{{1/2}}}t} \tau }} \right. \kern-0em} \tau }]} \right\}}}, \\ \end{gathered} $
где

$\begin{gathered} A = 2{{a}_{s}}{{c}_{{in}}} + {{b}_{s}} + {{(b_{s}^{2}~--{\text{ }}4a{{c}_{s}})}^{{1/2}}}; \\ B = 2{{a}_{s}}{{c}_{{in}}} + b--{{{{(}^{~}}b_{s}^{2}--4a{{c}_{s}})}^{{1/2}}}, \\ E = \exp [--{\text{ }}{{(~b_{s}^{2}--4{{a}_{s}}{{c}_{s}})}^{{1/2}}}t{\text{/}}\tau ]. \\ \end{gathered} $
(7)
$\begin{gathered} {\text{При}}\,\,t \to \infty \,\,E \to 0\,\,{\text{и}}\,\,c \to {{c}_{{ad}}}\,\,~ = ~ \\ = [{{(~b_{s}^{2}--4{{a}_{s}}{{c}_{s}})}^{{1/2}}}--{{b}_{s}}]{\text{/}}\left( {2{{a}_{s}}} \right) \approx \\ \approx 2({{c}_{t}}\tau {\text{/}}{{\tau }_{1}} + {{c}_{0}}\tau {\text{/}}{{\tau }_{0}}){\text{/}}\left( {1--{{c}_{t}}} \right). \\ \end{gathered} $

Слагаемое с зависящей от времени экспонентой E дает вклад в изменение c на небольшом начальном участке t ~ τ, где ct ≈ ctin. Этот вклад в уравнение (3) можно аппроксимировать δ – функцией, умноженной на интегральное изменение c на этом участке

(8)
$\begin{gathered} \Delta {{c}_{t}} = (1{\text{/}}{{\tau }_{0}})~\int\limits_0^\infty {dt[c(t) - {{c}_{{ad}}}]} \approx \\ \approx (\tau {\text{/}}{{\tau }_{0}})\ln \left( {1--{{c}_{{tin}}}} \right){\text{/}}\left( {1--{{c}_{{tin}}} + {{c}_{{in}}}} \right)], \\ \end{gathered} $
что эквивалентно скачку ct при t = 0.

Такой подход значительно упрощает анализ на основном временном интервале t > τ, так как позволяет свести систему уравнений всего лишь к одному решаемому аналитически уравнению путем замены c на cad, а начального значения ctin на $c_{{tin}}^{'}$ = = ctin + Δct. Решаем уравнение для ct на адиабатическом участке и получаем

(9)
$\begin{gathered} {{2t} \mathord{\left/ {\vphantom {{2t} {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}} = \int\limits_{c_{{tin}}^{'}}^{{{c}_{t}}} {\frac{{(1 - {{c}_{t}})d{{c}_{t}}}}{{{{c}_{0}}(1 - {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}}) - {{c}_{t}}({{c}_{0}} + {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}})}}} = \frac{1}{{{{c}_{0}} + {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}}}} \times \\ \times \,\,\{ {{c}_{t}}--c_{{tin}}^{'}--[1--{{c}_{0}}{{(1--{\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}})} \mathord{\left/ {\vphantom {{(1--{\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}})} {({{c}_{0}} + {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}}}}} \right. \kern-0em} {({{c}_{0}} + {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}}}})]{\kern 1pt} \,\, \times \\ \times \,\,{\text{ln}}\left[ {\frac{{{{c}_{t}} - {{c}_{0}}{{(1 - {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}})} \mathord{\left/ {\vphantom {{(1 - {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}})} {({{c}_{0}} + {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}})}}} \right. \kern-0em} {({{c}_{0}} + {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}})}}}}{{c_{{tin}}^{'} - {{{{c}_{0}}(1 - {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}})} \mathord{\left/ {\vphantom {{{{c}_{0}}(1 - {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}})} {({{c}_{0}} + {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}})}}} \right. \kern-0em} {({{c}_{0}} + {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}})}}}}} \right]. \\ \end{gathered} $

Таково поведение примесного содержания на дислокации в течение времени ожидания ta очередного термофлуктуационного скачка в соседнюю долину кристаллического рельефа. Полученное выражение (9) будет далее использоваться при более общем по сравнению с работой [20] описании длиннопробежного перемещения дислокации под действием внешнего напряжения с частичным увлечением примесной атмосферы, так как оно учитывает времена миграции примесей как в объеме кристалла τ0, так и в непосредственной окрестности дислокационного ядра τ1.

КОЭВОЛЮЦИЯ ДИСЛОКАЦИОННОЙ И ПРИМЕСНОЙ ПОДСИСТЕМ

Движение дислокации по периодическому рельефу кристаллической решетки на микроуровне осуществляется последовательными термоактивируемыми скачками на один период решетки со средним временем ожидания одного скачка ta. Примеси, оставленные в покинутой дислокацией долине кристаллического рельефа, стремятся релаксировать к новому положению дислокации. Так как энергетический рельеф в рассматриваемой модели привязан к дислокации и перемещается вместе с ней, на следующем шаге следует приписать обозначения d, ± новым узлам кристаллической решетки. Пусть, для определенности, дислокация движется, переходя от состояния d к состоянию +. При этом величины примесного содержания, достигнутые на предыдущем шаге к моменту скачка дислокации ta, будут играть роль начальных условий для релаксации концентраций на новом этапе $c_{{din}}^{{(2)}} = c_{ + }^{{(1)}}({{t}_{a}})$, $c_{{ - in}}^{{(2)}} = c_{d}^{{(1)}}({{t}_{a}})$. Новое состояние c+ возникает из резервуара и ему приписывается начальное содержание примесей $c_{{ + in}}^{{(2)}}$ = c0.

При описании движения дислокации как серии последовательных скачков будем использовать решение (9), подставляя в него каждый раз новые начальные условия. Эволюция кинетических зависимостей cd(t) для нескольких последовательных шагов, начиная от “свежей” дислокации (то есть не имеющей избыточного количества примесей по сравнению со средней их концентрацией в объеме кристалла c0), проиллюстрирована на рис. 2.

Рис. 2.

Вариация примесного содержания в дислокационном ядре (а) и во всей атмосфере (б) во время серии дислокационных скачков. Значения параметров: c0 = 0.01; τ0/τ = 13; τ1/τ = 21; c+in = 0.01; c–in = 0.015; cdin = 0.01.

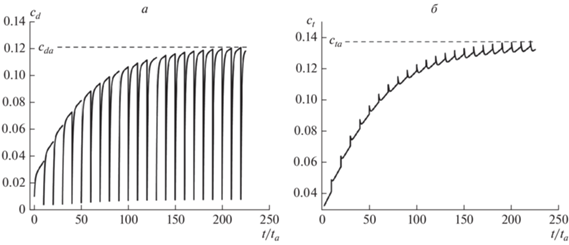
При любом начальном состоянии примесей в ядре после смещения дислокации на несколько периодов решетки устанавливается повторяющаяся на последующих шагах кинетическая зависимость cdst(t). Содержание примесей при таком движении дислокации будет характеризоваться амплитудными значениями cd(t) и ct(t) в интервале (0, ta) – cda и cta соответственно. Начальными условиями на новом этапе после перескока дислокации через барьер при итерации уравнения (9) являются

(10)
${{c}_{{tin}}} = {{c}_{0}} + {{c}_{{da}}} + {{c}_{{ + a}}} = ~\,\,{{c}_{0}} + {{c}_{{ta}}} - {{c}_{{ad}}}{\text{/}}2,$
(11)
${{c}_{{in}}} = ~\,\,{{c}_{0}} + {{c}_{{ta}}} - {{c}_{{ad}}},$
(12)
${{c}_{m}}_{0} = {{c}_{{ + in}}}--{{c}_{{ - in}}} = {{c}_{0}}--{{c}_{{da}}} = ~\,\,{{c}_{0}}--{{c}_{{ta}}} + {{c}_{{ad}}},~~~~~~~~$
где cta находится из (9) при t = ta.

При выходе на стационар уравнение (9) определяет ctas, если его подставить также в $c_{{tin}}^{'}$ = ctin + + Δct с использованием соотношений (10)–(12). Учитывая малость приращения полного числа примесей при каждом шаге дислокации в рассматриваемом случае низкой средней объемной концентрации c0$ \ll $ 1, можно привести уравнение (9) к более простому виду

(13)
$\begin{gathered} {{t}_{a}} \approx 0.5{{\tau }_{0}}\{ {{c}_{{ta}}}\tau {\text{/}}{{\tau }_{1}}--(1--{{c}_{{ta}}})[{{c}_{0}} + (\tau {\text{/}}{{\tau }_{0}}) \times \\ \times \,\,\ln (1--{{c}_{{ta}}})\left] {\} {\text{/}}} \right[{{c}_{0}}--{{c}_{{ta}}}({{c}_{0}} + \tau {\text{/}}{{\tau }_{1}})].~~~~~~~~ \\ \end{gathered} $

Зависимость стационарного амплитудного значения концентрации примесей в дислокационной атмосфере от времени ожидания смещения дислокации на период решетки ta или, эквивалентно, от ее средней скорости V = a/ta, даваемая соотношением (13), является основным результатом расчета и имеет многочисленные следствия.

МАКРОСКОПИЧЕСКАЯ ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ

Рассчитанные закономерности коэволюции примесных атомов с движущимися дислокациями можно применить к изучению влияния примесной подсистемы на макроскопические механические свойства кристаллов. Зацепление увлекаемых дислокациями примесей за кристаллическую решетку приводит к упрочнению материала. Скорость движения дислокации через барьеры в зависимости от однородной движущей силы может быть аппроксимирована, как это обычно делается [21], с помощью термоактивационного закона

(14)
$V = {{V}_{0}}\exp \left[ {--\frac{{{{E}_{{d0}}}{{{\{ 1 - {{{[{{{{\sigma }_{{ef}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{ef}}}} {{{\sigma }_{P}}}}} \right. \kern-0em} {{{\sigma }_{P}}}}]}}^{q}}\} }}^{p}}}}{{kT}}} \right].$

Здесь Ed0 – энергия активации движения дислокации в беспримесном материале при исчезающе малой нагрузке, σP – напряжение Пайерлса, σef – эффективное напряжение, в рассматриваемом случае учитывающее тормозящее влияние сегрегированных на дислокации примесей. Показатели степени q и p есть некоторые числа порядка единицы, зависящие от вида кристаллического рельефа. При гармоническом, так называемым синусоидальном, потенциальном рельефе кристаллической решетки показатели степени приблизительно равны: q ≈ 1, p ≈ 1.3, что и будет в дальнейшем использоваться для иллюстрации расчета.

В различных ситуациях эффективное напряжение может по-разному выражаться через концентрацию примесей в ядре дислокации. В случае, когда среднее расстояние между примесями a/cd меньше размера кинка dk ~ a(G/σP)1/2 (G – модуль сдвига) [22], можно использовать усредненное описание взаимодействия между примесями и дислокациями и характеризовать его некоторым тормозящим напряжением σi. Как показывают эксперименты со статическим старением, например [19], σi пропорционально избыточной примесной концентрации на дислокациях: σI = = β(cd – c0), что и будет приниматься далее. Коэффициент пропорциональности β может рассматриваться как некоторый феноменологический параметр. При этом входящее в энергию активации в (14) эффективное напряжение имеет вид σef = σ – σi = σ – β(cd – c0), где σ – внешнее прикладываемое напряжение.

Будем находить скорость пластического течения $\dot {\varepsilon }$ с помощью закона Орована $\dot {\varepsilon }$ = ρbV, в котором плотность дислокаций ρ приближенно считается постоянной. Здесь b – величина вектора Бюргерса дислокаций. Выражая скорость дислокации через $\dot {\varepsilon }$, преобразуем уравнение (13) к виду

(15)
$\begin{gathered} {{{\dot {\varepsilon }}}_{0}}{\text{/}}\dot {\varepsilon } = 0.5(a{{\tau }_{0}}{\text{/}}{{V}_{0}})\{ {{c}_{{ta}}}\tau {\text{/}}{{\tau }_{1}}--(1--{{c}_{{ta}}}) \times \\ \times \,\,[{{c}_{0}} + (\tau {\text{/}}{{\tau }_{0}})\ln (1--{{c}_{{ta}}})\left] {\} {\text{/}}} \right[{{c}_{0}}--{{c}_{{ta}}}({{c}_{0}} + \tau {\text{/}}{{\tau }_{1}})], \\ \end{gathered} $
где ${{\dot {\varepsilon }}_{0}}$ = ρbV0. Определяемая уравнением (15) зависимость деформирующего напряжения от скорости деформации $\dot {\varepsilon }$ проиллюстрирована на рис. 3.

Рис. 3.

Зависимость деформирующего напряжения от скорости деформации (а) при kT/E0 = 0.1 и температуры (б) при ${{\dot {\varepsilon }} \mathord{\left/ {\vphantom {{\dot {\varepsilon }} {{{{\dot {\varepsilon }}}_{0}}}}} \right. \kern-0em} {{{{\dot {\varepsilon }}}_{0}}}}$ = 10–4 и различных концентрациях примесей в объеме, указанных цифрами у кривых. Значения остальных параметров: Ei/E0 = 0.7; Ed/E0 = 1.4; p = 1.3; β = 0.6.

ТЕМПЕРАТУРНЫЕ АНОМАЛИИ ПЛАСТИЧНОСТИ

Как хорошо известно, при повышении температуры пластичность чистых (беспримесных) кристаллов, за исключением интерметаллидов и родственных им материалов, имеет тенденцию к повышению. Такое поведение представляется вполне естественным, так как повышение температуры усиливает флуктуации, способствующие преодолению тормозящих дислокации барьеров. Но в материалах, содержащих примеси, нередко в некоторых температурных интервалах наблюдается аномальный рост деформирующего напряжения с повышением температуры.

Подходящим кандидатом на роль механизма аномалии может служить динамическое деформационное старение дислокаций. При изменении температуры меняется баланс прибывающих в дислокационное ядро и покидающих его примесей и, в частности, возможно увеличение примесного содержания с повышением температуры. Это приведет к повышению тормозящего примесного вклада в эффективное движущее дислокации напряжение, как это иллюстрируется на рис. 3б.

Важной измеряемой экспериментально характеристикой механических свойств материалов является скоростная чувствительность деформирующего напряжения dσ/dln$\dot {\varepsilon }$. Дифференцируя уравнение (15), получаем

(16)
$\begin{gathered} d\sigma {\text{/}}d\ln \dot {\varepsilon } = \beta d{{c}_{d}}{\text{/}}d\ln \dot {\varepsilon } + \\ + \,({{\sigma }_{P}}{\text{/}}p){{(kT{\text{/}}{{E}_{d}}_{0})}^{{1/p}}}{{[\ln ({{{\dot {\varepsilon }}}_{0}}{\text{/}}\dot {\varepsilon })]}^{{1/}}}{{^{p}}^{{--1}}}. \\ \end{gathered} $

Содержание малоподвижных примесей в ядрах дислокаций убывает по мере увеличения скорости дислокаций, что дает отрицательный вклад в скоростную чувствительность деформирующих напряжений dσ/dln$\dot {\varepsilon }$ и может служить причиной нестабильности пластического течения материала, проявляющейся в эффекте Портевена–Ле Шателье [12, 13].

Рисунок 4 иллюстрирует температурное поведение скоростной чувствительности деформирующего напряжения dσ/dln$\dot {\varepsilon }$, рассчитываемое с помощью уравнений (14), (15). Как видно из рисунка, при достаточно большой средней концентрации примесей в объеме материала в некотором температурном интервале скоростная чувствительность деформирующего напряжения имеет аномальный отрицательный знак. На рис. 4б показано теоретическое описание экспериментальных данных для α-Fe [23]. Эти данные выбраны для иллюстрации, так как по утверждению получивших их авторов, механические свойства, изучаемые в условиях насыщения при циклической нагрузке, проявляют повышенную чувствительность к влиянию примесей.

Рис. 4.

Температурная зависимость скоростной чувствительности R = dσ/dln$\dot {\varepsilon }$ деформирующего напряжения, иллюстрируемая теоретическим расчетом при различных значениях средней концентрации примесей в объеме, указанных цифрами у кривых. Скоростная чувствительность нормирована на напряжение Пайерлса σP, значения параметров: Ei/E0 = 0.7, E1/E0 = 2.5, Ed/E0 = 1.5, p = 1.3, β/σP = 0.6, $\dot {\varepsilon }$/${{\dot {\varepsilon }}_{0}}$ = 10–4. На вставке изображена теоретическая кривая, подогнанная под экспериментальные данные [22] при c0 ≈ 10–4, σP ≈ 362 MПa, β/σP ≈ 0.23, E0 ≈ 0.385 эВ, $\dot {\varepsilon }$/${{\dot {\varepsilon }}_{0}}$ = 10–4.

Подобные вышеприведенным особенности неоднократно наблюдались также в экспериментах с многочисленными другими материалами: в металлах с ОЦК структурой Mo, V и других, в разупорядоченных твердых растворах, при призматическом скольжении в металлах с ГПУ структурой Ti, Zr, Be и интерметаллидах (см. обзор в [2, 3]). Достаточно большое увеличение содержания примесей в ядрах способно полностью блокировать движение дислокаций или может являться причиной перестройки строения ядер, как это обсуждалось применительно к углероду или водороду в α-Fe и W [9–11, 24, 25].

Итак, в работе развита модель для описания динамического деформационного старения металлов с ОЦК структурой кристаллической решетки, вызванное взаимодействием дислокационной и примесной подсистем материала. Короткомасштабный характер потенциального рельефа (барьеров Пайерлса), контролирующего перемещение дислокаций, приводит к коренному отличию закономерностей в ОЦК металлах и в традиционно изучаемых в связи с эффектом Портевена–Ле Шателье материалах с ГЦК структурой. Главным отличием является частичное увлечение примесей при перемещении дислокаций. Общепринятое для ГЦК материалов с низким кристаллическим рельефом континуальное описание с привлечением механизма коттрелловской диффузии применительно к ОЦК металлам в определенной области температур и скоростей деформации должно быть заменено дискретным описанием с рассмотрением короткомасштабных процессов типа релаксации Снука. Результаты расчета позволяют проследить основные качественные закономерности влияния примесной подсистемы и оценить роль различных материальных параметров.

Список литературы

  1. Фридель Ж. Дислокации. М.: Мир, 1967. 643 с.

  2. Messerschmidt U. Dislocation dynamics during plastic deformation. Berlin, Heidelberg: Springer Series in Material Science, 2010. 503 p.

  3. Caillard D., Martin J.L. Thermally activated mechanisms in crystal plastisity. Amsterdam: Pergamon, 2003. 433 p.

  4. Nadgornyi E. // Progr. Mater. Sci. 1988. V. 31. P. 1.

  5. Katzarov I.H., Pashov D.L., Paxton A.T. // Phys. Rev. Mater. 2017. V. 1. Art. No. 033602.

  6. Pink E., Arsenault R.J. // Progr. Mater. Sci. 1979. V. 24. P. 1.

  7. Trinkle D.R., Woodward C. // Science. 2005. V. 310. P. 1665.

  8. Петухов Б.В. // Кристаллография. 2007. Т. 52. С. 113; Petukhov B.V. // Crystallography Rep. 2007. V. 52. P. 112.

  9. Romaner L., Ambrosch-Draxl C., Pippan R. // Phys. Rev. Lett. 2010. V. 104. Art. No. 195503.

  10. Ventelon L., Lüthi B., Clouet E. et al. // Phys. Rev. B. 2015. V. 91. Art. No. 220102 (R).

  11. Grigorev P., Swinburne T.D., Kermode J.R. // Phys. Rev. Mater. 2020. V. 4. Art. No. 023601.

  12. Portevin A., Le Chatelier F. // Trans. Amer. Soc. St. Tr. 1924. V. 5. P. 457.

  13. Rizzi E., Hähner P. // Int. J. Plasticity. 2004. V. 20. P. 121.

  14. Yoshinaga H., Morozumi S. // Philos. Mag. 1971. V. 23. № 186. P. 1351.

  15. Schoeck G., Seeger A. // Acta Metall. 1959. V. 7. P. 469.

  16. Xиpт Дж., Лoтe И. Teopия диcлoкaций. M.: Aтoмиздaт, 1972. 598 c.

  17. Петухов Б.В. Динамика дислокаций в кристаллическом рельефе. Дислокационные кинки и пластичность кристаллических материалов. Saarbrücken: Lambert Academic Publ., 2016. 385 p.

  18. Louat N. // Scr. Metall. 1981. V. 15. P. 1167.

  19. Park S.C., Beckerman L.P., Reed-Hill R.E. // Metallurg. Trans. A. 1983. V. 14 A. P. 463.

  20. Петухов Б.В. // Кристаллография. 2009. Т. 54. № 1. С. 85.

  21. Kocks U.F., Argon A.S., Ashby M.F. // Progr. Mater. Sci. 1975. V. 19. P. 1.

  22. Petukhov B.V. // Mater. Sci. Engin. A. 1997. V. 234–236. P. 177.

  23. Maruyama K., Meshii M. // Mater. Sci. Engin. 1984. V. 67. P. 69.

  24. De A.K., De Blauwe K., Vandeputte S., De Cooman B.C. // J. Alloys Compounds. 2000. V. 310. P. 405.

  25. Itakura M., Kaburaki H., Yamaguchi M., Okita T. // Acta Mater. 2013. V. 61. P. 6857.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал