Известия РАН. Серия физическая, 2022, T. 86, № 12, стр. 1678-1684

ВВЕДЕНИЕ

Терагерцовые технологии имеют широкий спектр применения. Благодаря их быстрому развитию открываются широкие возможности для исследователей в области физики, химии, биологии, медицины и т.д. [1, 2]. Говоря о методах генерации терагерцового излучения, следует выделить метод, основанный на оптическом выпрямлении, как наиболее эффективный среди прочих [3–5]. Генерируемый терагерцовый импульс содержит приблизительно один период колебаний в соответствующем диапазоне. Это означает, что сигнал обладает свойствами чрезвычайно коротких импульсов. Таким образом, известный подход медленно меняющейся огибающей в данном случае неприменим в теоретическом анализе.

Впервые механизм оптического выпрямления был теоретически и экспериментально исследован в [3–5]. Условие синхронизма, необходимое для эффективной генерации, имеет черенковскую форму ${{\vartheta }_{g}}\cos \Theta = {{\vartheta }_{{ph}}}.$ Здесь ${{\vartheta }_{g}}$ – групповая скорость оптического импульса, ${{\vartheta }_{{ph}}}$ – фазовая скорость терагерцового сигнала, $\Theta $ – угол между направлениями распространения оптического и терагерцового сигналов [3–5]. Хорошо известное условие резонанса Захарова–Бенни (ЗБ) ${{\vartheta }_{g}} = {{\vartheta }_{{ph}}}$ следует из условия Черенкова в коллинеарном режиме ($\Theta = 0$) [6, 7].

Для описания процесса генерации терагерцового импульса из широкополосного оптического импульса мы используем приближение медленно меняющейся огибающей (ММО) $\psi $ для электрического поля оптической составляющей и приближение однонаправленного распространения [8] для электрического поля ${{E}_{T}}$ терагерцовой компоненты [9, 10]. Это дает нам систему двух нелинейно-связанных уравнений, аналогичную интегрируемой системе Ядзимы–Ойкавы (ЯО), полученной ранее для описания взаимодействия ионно-звуковой и ленгмюровской волн в плазме [11].

В применении к генерации широкополосной терагерцовой составляющей с помощью квазимонохроматического оптического сигнала система ЯО описывает случай резонанса ЗБ, когда собственная нелинейность терагерцовой составляющей пренебрежимо мала. Соответствующее солитонное решение представляет собой связанное стационарное состояние оптической и терагерцовой компонент со сдвигом в “красную” область несущей частоты оптического импульса [9, 10]. Данный сдвиг четко обозначает физический механизм генерации как результат распада каждого фотона оптического диапазона на терагерцовый фотон и другой “покрасневший” оптический фотон. В [12] обозначенный “красный” сдвиг был продемонстрирован экспериментально.

В [13] cистема ЯО была обобщена на случай интенсивного и короткого оптического сигнала с относительной длительностью всего до нескольких световых колебаний. В этом случае для оптической компоненты необходим учет групповой дисперсии третьего порядка, дисперсии квадратичной оптико-терагерцовой нелинейности и бездисперсионной кубической (керровской) нелинейности. В то же время в данном обобщении при описании терагерцовой составляющей учтена ее дисперсия, собственная квадратичная нелинейность и квадратичная нелинейность, несущая информацию о фазе оптического импульса (фазовая нелинейность). В [13] показана интегрируемость обобщенной системы ЯО при жестких ограничениях на коэффициенты соответствующих уравнений. Там же представлено односолитонное решение данной системы.

Отмеченные выше жесткие ограничения на коэффициенты не могут быть реализованы в экспериментальных условиях. Поэтому в настоящей работе процесс генерации широкополосного терагерцового сигнала мощным оптическим импульсом длительностью в несколько колебаний исследуется с помощью численного моделирования, без упомянутых ограничений на коэффициенты.

ПОСТАНОВКА ЗАДАЧИ

Обобщенная система ЯО, описывающая представленный во Введении процесс генерации, при выполнении условия ЗБ имеет вид [13]:

Здесь $\bar {\tau } = t - {{\bar {z}} \mathord{\left/ {\vphantom {{\bar {z}} {{{\vartheta }_{g}}}}} \right. \kern-0em} {{{\vartheta }_{g}}}} = t - {{\bar {z}} \mathord{\left/ {\vphantom {{\bar {z}} {{{\vartheta }_{T}}}}} \right. \kern-0em} {{{\vartheta }_{T}}}},$ $\alpha = \frac{\pi }{c}{{\left( {\frac{{{{\partial }^{2}}\chi }}{{\partial {{\omega }^{2}}}}} \right)}_{{\omega = 0}}},$ β = = $\frac{{4\pi {{\chi }^{{\left( 2 \right)}}}\left( {0;0} \right)}}{c},$ σ = $\frac{{4\pi {{\chi }^{{\left( 2 \right)}}}\left( {\omega ; - \omega } \right)}}{{c{{n}_{T}}}},$ q = $\frac{{4\pi }}{c}{{\left( {\frac{{\partial {{\chi }^{{\left( 2 \right)}}}}}{{\partial {{\omega }_{1}}}}} \right)}_{{\left| \begin{subarray}{l} {{\omega }_{1}} = - \omega \\ {{\omega }_{2}} = \omega \end{subarray} \right.}}},$ k₂ = $\frac{{2\pi }}{c}\left( {2\frac{{\partial \chi }}{{\partial \omega }} + \omega \frac{{{{\partial }^{2}}\chi }}{{\partial {{\omega }^{2}}}}} \right),$ ${{k}_{3}} = \frac{{2\pi }}{c}\left( {3\frac{{{{\partial }^{2}}\chi }}{{\partial {{\omega }^{2}}}} + \omega \frac{{{{\partial }^{3}}\chi }}{{\partial {{\omega }^{3}}}}} \right),$ $a = \frac{{4\pi \omega }}{c}{{\chi }^{{(2)}}}(\omega ,0),$ $b = \frac{{4\pi }}{c}{{\chi }^{{\left( 2 \right)}}}\left( {\omega ;0} \right),$ $\mu = \frac{{4\pi }}{c} \times $ $ \times \,\,\left( {{{\chi }^{{\left( 2 \right)}}}\left( {\omega ;0} \right) + \omega \frac{\partial }{{\partial \omega }}{{\chi }^{{\left( 2 \right)}}}\left( {\omega ;0} \right)} \right),$ $\varepsilon = \frac{{6\pi \omega }}{c} \times $ $ \times \,\,{{\chi }^{{\left( 3 \right)}}}\left( {\omega ,\omega , - \omega } \right)\chi ,$ ${{\chi }^{{(2)}}}$ и ${{\chi }^{{(3)}}}$ – линейная, квадратичная и кубическая восприимчивости соответственно, $\omega $ – несущая частота оптического импульса, ${{n}_{T}}$ – терагерцовый показатель преломления, $c$ – скорость света в вакууме.

В правой части первого уравнения (1) первые два слагаемых описывают дисперсию групповой скорости (ДГС) второго и третьего порядков соответственно оптической компоненты. Третье слагаемое описывает квадратичную оптико-терагерцовую нелинейность, а четвертое и пятое слагаемые – дисперсию данной нелинейности. Последнее слагаемое соответствует керровской нелинейности.

В правой части второго уравнения системы (1) первые два слагаемых описывают соответственно собственные дисперсию и нелинейность терагерцовой компоненты. Третье, квадратично-нелинейное, слагаемое играет ключевую роль в генерации терагерцового сигнала. Последнее слагаемое соответствует упомянутой во Введении фазовой нелинейности [14].

Отметим, что при ${{k}_{3}} = b = \mu = \alpha = \beta = q = 0$ (1) переходит в систему ЯО.

При численном моделировании используем систему (1) в нормированном виде:

Поскольку одна из наших целей состоит в том, чтобы проследить зависимость протекающих процессов от длительности импульса, мы ввели в (2) параметр $N = \omega {{\tau }_{0}},$ определяющий количество осцилляций. В (2) введены также нормированные параметры $\bar {\psi } = \psi {{\psi }_{0}},$ $\bar {E} = {{E}_{T}}{{\psi }_{0}},$ ${{\psi }_{0}}$ – пиковая амплитуда оптического сигнала на входе, $\bar {\tau } = \tau {{\tau }_{0}},$ $\bar {z} = z{{l}_{{nl}}},$ ${{l}_{{nl}}} = {1 \mathord{\left/ {\vphantom {1 {\left( {a{{\psi }_{0}}} \right)}}} \right. \kern-0em} {\left( {a{{\psi }_{0}}} \right)}},$ ${{D}_{{k2}}} = {\text{sig}}n({{k}_{2}})\frac{{{{l}_{{nl}}}}}{{{{l}_{{dis2}}}}},$ ${{D}_{{k3}}} = \frac{{{{l}_{{nl}}}}}{{{{l}_{{dis3}}}}},$ ${{l}_{{dis2}}} = \frac{{2\tau _{0}^{2}}}{{\left| {{{k}_{2}}} \right|}},$ ${{l}_{{dis3}}} = \frac{{6\tau _{0}^{3}}}{{{{k}_{3}}}},$ параметр μ переходит в $\frac{{\mu {{\psi }_{0}}}}{{{{\tau }_{0}}}}{{l}_{{nl}}} \approx \frac{2}{N},$ b – в $\frac{{b{{\psi }_{0}}}}{{{{\tau }_{0}}}}{{l}_{{nl}}} \approx \frac{1}{N},$ α – в $\frac{{\alpha {{l}_{{nl}}}}}{{\tau _{0}^{3}}} \approx \frac{1}{{4{{N}^{2}}}},$ β – в $\frac{{\beta {{\psi }_{0}}}}{{{{\tau }_{0}}}}{{l}_{{nl}}} \approx \frac{1}{N},$ $q$ – в $\frac{{q{{\psi }_{0}}}}{{\tau _{0}^{2}}}{{l}_{{nl}}} \approx \frac{1}{N},$ ${{D}_{\sigma }} = \frac{{\sigma {{\psi }_{0}}{{l}_{{nl}}}}}{{{{\tau }_{0}}}},$ $\gamma = \frac{{\varepsilon \psi _{0}^{2}{{l}_{{nl}}}}}{{{{\tau }_{0}}}},$ ${{\tau }_{0}}$ – длительность оптического импульса на входе. В системе (2) использованы соотношения $\frac{q}{\sigma } = \frac{b}{a},$ μ = 2b между коэффициентами системы (1) [13].

Так как на вход среды подается только оптический импульс, то граничное условие запишем в виде:

Система (2) обладает интегралами движения, которые мы отслеживаем в наших расчетах:

В (4), (5) ${{L}_{\tau }}$ – безразмерный интервал времени, в течение которого моделируется взаимодействие лазерного импульса со средой. Параметр N₀ в (4) пропорционален числу фотонов в оптическом импульсе. Часть энергии каждого фотона уходит в терагерцовую область. При этом число терагерцовых фотонов ${{N}_{T}} = \int_{ - {{L}_{\tau }}}^{{{L}_{\tau }}} {E_{\tau }^{2}d\tau } $ увеличивается, в то время как частота оптических фотонов уменьшается. В (5) A_T – электрическая площадь широкополосного импульса.

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

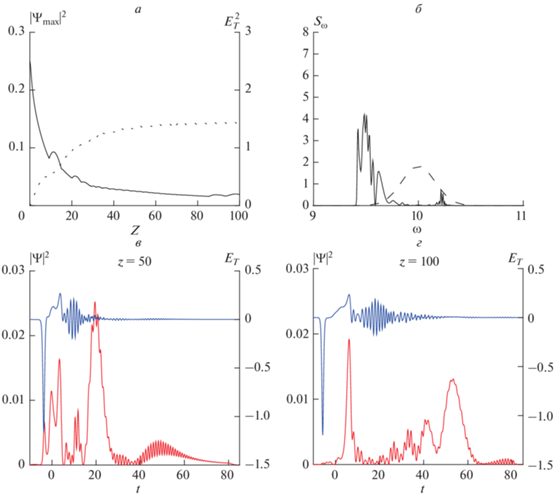
В серии численных экспериментов на основе безразмерной системы (2), (3) использовался численный метод, сохраняющий разностные аналоги интегралов (4), (5) [15]. Мы ожидали, что укорачивание импульса (уменьшение числа колебаний N) приведет к формированию и устойчивому распространению связанного оптико-терагерцового солитона. Наиболее ярко выраженные результаты в случае нормальной дисперсии второго порядка представлены ниже. Сначала мы моделировали достаточно длинный оптический импульс ($N = 100$), запускаемый в кристалл (например, ZnTe), не учитывая нелинейность третьего порядка. Результаты, представленные на рис. 1, показывают, что, хотя сигнал терагерцового диапазона генерируется, солитон оптического терагерцового диапазона не формируется. При уменьшении начальной длительности импульса до $N = 3,$ мы наблюдаем формирование и устойчивое распространение такого солитона (рис. 2, 3).

На рис. 2 показан переходный случай, когда число колебаний начального импульса $N = 10.$ Несмотря на явные изменения профилей обеих компонент, сценарий процесса аналогичен случаю $N = 100.$ Ситуация резко меняется для ультракоротких импульсов, когда $N = 3.$ Мы наблюдаем формирование стабильного оптического солитона (рис. 3). При этом виден типичный красно-смещенный широкополосный спектр оптического импульса (рис. 3б), а несолитонная часть терагерцовой составляющей имеет вид функции Эйри за счет дисперсии третьего порядка (рис. 3в и 3г). Аналогичная оптико-терагерцовая динамика отмечена в работе [16], где не учитывалась керровская нелинейность.

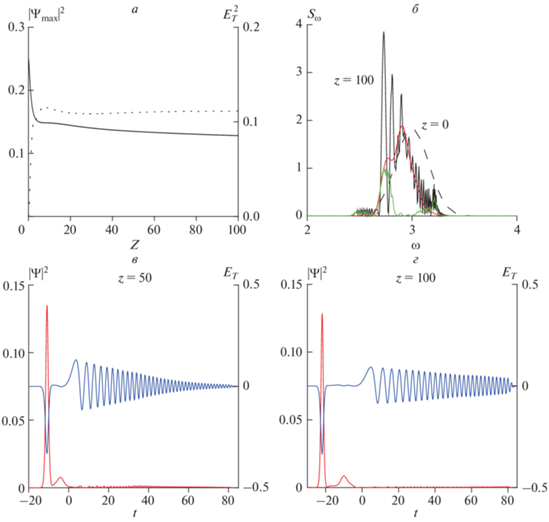
При учете керровской нелинейности (вплоть до $\gamma = 1$) мы по-прежнему наблюдаем устойчивый солитон оптико-терагерцового диапазона, обладающий теми же свойствами, что и в предыдущем случае (рис. 4). Увеличивая коэффициент керровской нелинейности до $\gamma = 3,$ мы видим разрушение солитона. Известно, что при нормальной ДГС второго порядка и фокусирующей керровской нелинейности устойчивый оптический солитон не образуется. В этом случае необходим учет квадратичной нелинейности и ДГС третьего порядка. С уменьшением количества осцилляций $N,$ содержащихся в оптическом импульсе, возрастает удельный вес дисперсии квадратичной нелинейности (четвертое и пятое слагаемые в правой части первого уравнения системы (2)), которая независимо от знака ДГС способствует формированию устойчивого одномерного солитона. При этом уменьшается деструктивная роль фокусирующей керровской нелинейности вкупе с нормальной ДГС. При увеличении же количества осцилляций данная роль становится более значительной, что препятствует формированию солитона и в конце концов приводит к потере его устойчивости.

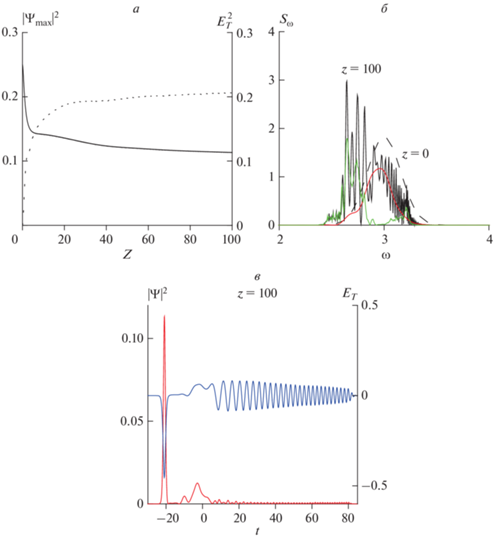
Мы также моделировали процесс оптического выпрямления с учетом аномальной дисперсии второго порядка D_k2 < 0 и фокусирующей керровской нелинейности γ < 0. Сценарий генерации и распространения терагерцового импульса существенно отличается от описанного выше для нормальной дисперсии групповой скорости и нелинейности фокусировки. Хотя мы укорачиваем запускаемый оптический импульс до $N = 3,$ оптико-терагерцовый солитон не формируется. Видно распространение оптического солитона, сопровождаемого суперконтинуумом, в терагерцовом диапазоне. В этом случае на начальной стадии генерации превалирует сугубо оптическая керровская нелинейность фокусирующего характера, которая вкупе с аномальной ДГС приводит к устойчивому формированию хорошо известного оптического солитона. Затем за счет квадратичной нелинейности, описываемой третьим и четвертым слагаемыми в правой части второго уравнения системы (2), генерируется терагерцовый суперконтинуум. Здесь важная роль принадлежит дисперсии и нелинейности терагерцового диапазона (см. первые два слагаемых в правой части того же уравнения). По сути, мы имеем дело с генерацией суперконтинуума, которая описывается неоднородным уравнением Кортевега–де Вриза (КдВ), где оптический солитон выполняет роль внешнего заданного поля. Хорошо известно соответствующее автомодельное решение КдВ, выражающееся через функцию Эйри [17].

ЗАКЛЮЧЕНИЕ

Выполнено численное исследование генерации импульсов терагерцового диапазона в процессе оптического выпрямления. Для моделирования мы используем обобщенную систему ЯО с учетом бездисперсионной кубической нелинейности. Эта система позволяет рассматривать оптические импульсы длительностью в несколько колебаний.

В случае нормальной ДГС второго порядка при отсутствии керровской нелинейности мы демонстрируем образование солитона оптико-терагерцового диапазона при уменьшении длительности входного оптического импульса. Наиболее яркое распространение устойчивого связанного солитона показано для числа осцилляций N = 3. Данный режим распространения сопровождается характерным красным смещением широкополосного спектра оптического импульса. При этом генерируется также несолитонная часть терагерцовой составляющей, связанная с терагерцовой дисперсией третьего порядка.

Учет керровской нелинейности приводит к изменению динамики обеих компонент. В случае нормальной дисперсии второго порядка групповой скорости и фокусирующей кубической нелинейности при укорочении начального оптического импульса до N = 3 происходит захват оптико-терагерцового импульса, устойчиво распространяющегося на расстояние до 100 нелинейных длин.

Исследование выполнено при поддержке Междисциплинарной научно-образовательной школы Московского университета “Фотонные и квантовые технологии. Цифровая медицина”.