Известия РАН. Серия физическая, 2022, T. 86, № 2, стр. 170-174

ВВЕДЕНИЕ

Аморфные магнитные микропровода на протяжение последних десятилетий являются предметом многочисленных научных исследований. Широкое разнообразие существующих и будущих приложений на их основе определяет практический исследовательский интерес к этому классу материалов. При этом они по-прежнему актуальны и с фундаментальной точки зрения, поскольку являются ярким модельным объектом физики микромагнитных структур.

Особенности процесса изготовления аморфных магнитных микропроводов методами быстрой закалки из расплава оказывают сильное влияние на их магнитные свойства. Механические напряжения, возникающие при охлаждении расплава, за счет магнитоупругой анизотропии обеспечивают появление пространственного распределения направлений преимущественной ориентации намагниченности и, как следствие, сложной микромагнитной структуры проводов. Обычно их доменная структура может быть описана моделью керн-оболочка: осевое направление намагничивания типично для центральной части провода – керна, а в оболочке наблюдается радиальное либо циркулярное преимущественное направление намагниченности в зависимости от знака магнитострикции сплава [1–4].

Микромагнитная структура проводов определяет их отклик на внешнее магнитное поле. Особенности микромагнитной структуры определяют механизмы процессов перемагничивания и, следовательно, оказывают сильное влияние на их поведение в магнитном поле. В частности, бистабильность (гигантский скачок Баркгаузена) связана с изменением направления намагниченности керна [5]. Высокие значения магнитной проницаемости аморфных микропроводов обеспечивают появление в них гигантского магнитоимпедансного эффекта (ГМИ) [6], который также сильно зависит от типа магнитной анизотропии образца [7]. Полевые зависимости импеданса различны для микропроводов с радиально и циркулярно намагниченной оболочкой. В сочетании с относительно низкой электрической проводимостью, эти свойства и эффекты позволили аморфным микропроводам открыть перспективы практических приложений. В частности, магнитная бистабильность может использоваться в логических устройствах. Для хранения информации может быть использовано токовое перемагничивание керна микропровода [8], в том числе переменным током [9]. В последнем случае значительно снижается необходимая амплитуда пропускаемого тока, что позволяет снизить тепловые потери, а также избежать ухудшения магнитных характеристик образцов при нагреве. Эффект ГМИ уже активно используется в области сенсорики [10]. Защитные метки также могут быть созданы с использованием микропроводов [11]. Также ранее была продемонстрирована возможность создания микророботов на основе аморфных проводов для биомедицинских приложений [12].

Важность информации о микромагнитной структуре аморфных микропроводов, тем не менее, сопряжена с осложнениями, вызванными ограниченными возможностями экспериментального изучения их свойств. Достоверные данные могут быть получены о поверхностных (например, магнитооптическими методами [13] или методом Биттера [14]) свойствах или интегральных объемных свойствах [15]. Внутренняя структура же определяется косвенными методами по совокупности экспериментальных данных. В нескольких работах, посвященных рентгеновской микротомографии (например, [16, 17]), описаны ограничения данного метода, которые в первую очередь касаются предельных размеров образца (порядка 5 мкм).

Тем не менее, ограниченные возможности экспериментальных исследований тонких микромагнитных структур могут быть компенсированы симуляционными подходами [18]. Таким образом, полное описание микромагнитной структуры и механизмов перемагничивания требует не только комплексного экспериментального исследования, но и их численного моделирования с учетом полученных экспериментальных данных. Моделирование перемагничивания на микроуровне необходимо для понимания основных особенностей таких процессов и дальнейшего прогнозирования возможностей управления свойствами аморфных материалов.

Микромагнитное моделирование аморфных магнитных микропроводов в настоящее время сосредоточено на анализе сложных равновесных микромагнитных структур [19] или же топологии доменной стенки [20] в масштабируемых объектах. В данной же работе проводится полноразмерное моделирование процессов перемагничивания микропроводов с различными знаками магнитострикции внешним однородным магнитным полем или магнитным полем электрического тока для определения вкладов различных механизмов перемагничивания.

МЕТОДИКА РАСЧЕТА

Микромагнитное моделирование проводилось с помощью пакета OOMMF [21]. Область моделирования представляла собой цилиндр диаметром 4 мкм и длиной 100 мкм. Такие размеры позволяют приблизить расчетную область к геометрии образцов, используемых в экспериментах, и в то же время требуют небольших вычислительных мощностей. Стоит также отметить, что данные параметры позволяют наиболее наглядно продемонстрировать влияние размагничивания на микромагнитную структуру. Расчеты проводились с использованием прямоугольной сетки с размером ячейки 0.25 мкм. Для обменной жесткости A использовались значения в диапазоне 10^–12–10^–10 Дж ∙ м^–1, которые являются типичными для сплавов на основе железа и кобальта. Намагниченность насыщения M_s варьировалась в диапазоне 100–800 кА ∙ м^–1, что также соответствует характерным для аморфных сплавов значениям [2].

Магнитоупругая анизотропия задавалась векторным полем одноосной анизотропии с пространственным распределением константы анизотропии K_me и направлений оси легкого намагничивания. Константа анизотропии определялась по формуле:

где – ${{\lambda }_{s}},$ константа магнитострикции, ${{\sigma }_{{ii}}}~$ – преобладающая компонента тензора упругих напряжений. Значения ${{\sigma }_{{ii}}}~$были рассчитаны и описаны в [2, 3] для микропроводов с параметрами, соответствующими сплаву Fe_77.5Si_7.5B₁₅ с ${{\lambda }_{s}}$ = 25 ∙ 10^–6, и в [4] для микропроводов с параметрами, соответствующими сплаву Сo₇₅Si₁₅B₁₀ с ${{\lambda }_{s}}$ = –4 ∙ 10^–6.

Направления осей легкого намагничивания также можно определить из распределений компонент тензора упругих напряжений. Для микропроводов с положительной магнитострикцией направление оси легкого намагничивания совпадает с направлением преобладающих растягивающих напряжений и перпендикулярно направлению сжимающих напряжений [2, 3]. Рассчитанная координата смены направления преимущественной ориентации намагниченности составила 0.78 радиуса для образца FeSiB с толщиной жилы 3.65 мкм в стеклянной оболочке толщиной 7.5 мкм [2]. Для проволок с отрицательной константой магнитострикции соотношение обратное: направление оси легкого намагничивания совпадает с направлением преобладающих сжимающих напряжений и перпендикулярно направлению растягивающих напряжений. Таким образом, в центральной части провода направление преимущественной ориентации намагниченности также совпадает с осью микропровода, а затем (при радиальной координате 0.46 радиуса микропровода CoSiB с произвольным диаметром ферромагнитно й жилы без стеклянной оболочки) сменяется циркулярным [4].

Равновесное состояние намагниченности, соответствующее минимуму свободной энергии, определялось с помощью метода сопряженных градиентов. Полученное распределение намагниченности затем рассматривалось как начальное состояние при моделировании перемагничивания микропровода внешним магнитным полем или током.

Изменения намагниченности под действием приложенного магнитного поля рассчитывались с помощью решения уравнения Ландау–Лифшица–Гильберта классическим методом Рунге–Кутта.

Для моделирования перемагничивания микропровода внешним магнитным полем использовалось однородное поле амплитуды 10 кА ∙ м^–1 (что составляет порядка $3{{H}_{k}}$ для провода с положительной магнитострикцией и порядка $100{{H}_{k}}$ для провода с отрицательной магнитострикцией, где ${{H}_{k}} = ~\frac{{2{{K}_{{me}}}}}{{{{M}_{s}}}}$ – поле анизотропии), прикладываемое вдоль оси микропровода. Для токового же перемагничивания магнитное поле задавалось в виде векторного поля с направлением, совпадающим с азимутальным единичным вектором, и амплитудой, зависящей от радиальной координаты.

В квазистатическом приближении решение уравнений Максвелла позволяет получить пространственное распределение плотности переменного тока в проводнике. В случае цилиндрической проволоки зависимость плотности тока от радиальной координаты имеет вид:

где $j\left( R \right)$ – плотность тока на поверхности проводника, ${{J}_{0}}$ – функция Бесселя нулевого порядка, $\kappa = \frac{{{\text{\;}}\sqrt {2i} }}{{{\delta }}}$ – квазиволновое число, ${{\delta }} = {\text{\;}}\frac{1}{{\sqrt {{{\pi }}f\sigma {{{{\mu }}}_{{{\varphi }}}}{{{{\mu }}}_{0}}} }}$ – параметр скин-слоя, f – частота тока, ${{{{\mu }}}_{{{\varphi }}}}$ – циркулярная компонента магнитной проницаемости, ${{{{\mu }}}_{0}}$ – магнитная постоянная, ${{\sigma }}$ – электрическая проводимость [22]. Таким образом, согласно теореме о циркуляции магнитного поля, мгновенные значения величины магнитного поля: где ${{I}_{0}}$ – амплитуда полного пропускаемого тока, а ${{J}_{1}}$ – функция Бесселя первого порядка. Функция (3) отличается от линейной функции, описывающей радиальную зависимость амплитуды поля при отсутствии скин-эффекта. Это отклонение в совокупности с описанными особенностями микромагнитной структуры проводов, в частности, может приводить к более существенной разнице между вкладами различных механизмов перемагничивания и, следовательно, оказывать сильное влияние на магнитный отклик образца.

Как видно из выражения (3), магнитное поле и магнитная проницаемость взаимозависимы. В качестве опорного значения для получения радиальной зависимости величины магнитного поля среднее значение магнитной проницаемости считалось равным 5000. В модели рассматривалось поле с амплитудой 10 кА ∙ м^–1 на поверхности микропровода, изменяющееся с частотой 100 МГц по гармоническому закону. Полученная зависимость была аппроксимирована полиномиальной функцией для задания пространственного распределения амплитуды магнитного поля в модели.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Для микропровода с положительной константой магнитострикции равновесное распределение намагниченности представляет собой структуру с намагниченной вдоль оси микропровода центральной частью (керном) и радиально намагниченной приповерхностной областью (рис. 1а). При этом, на конце микропровода можно увидеть образование концевых доменов, возникающих из-за влияния размагничивающего поля. При увеличении постоянной обмена А изменяется вид концевого домена: он занимает меньшую долю длины провода, но увеличивается в диаметре, приближаясь к полному диаметру керна.

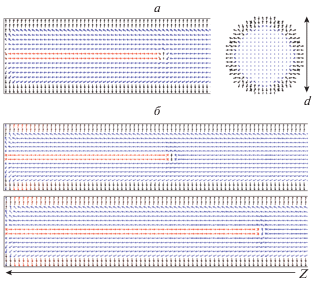
При приложении однородного магнитного поля вдоль оси микропровода начало процесса перемагничивания сопровождается ростом объема концевого домена (рис. 1б). Быстрое распространение доменной границы вдоль оси провода обеспечивает перемагничивание керна скачком, что многократно подтверждалось в экспериментальных исследованиях аморфных магнитных микропроводов (гигантский скачок Баркгаузена) [5, 23].

Для провода с отрицательной константой магнитострикции в равновесном состоянии центральная часть микропровода также намагничена вдоль его оси, а приповерхностная область намагничена циркулярно (рис. 2а). При этом в торцевой части провода заметна переходная область с постепенным разворотом намагниченности от центра к внешнему краю. При приложении магнитного поля вдоль оси микропровода намагниченность в приповерхностной циркулярной области отклоняется от первоначальной ориентации к направлению поля (рис. 2б), что обеспечивает безгистерезисное поведение в области малых полей и соответствует экспериментальным данным об особенностях перемагничивания проводов данного типа [23].

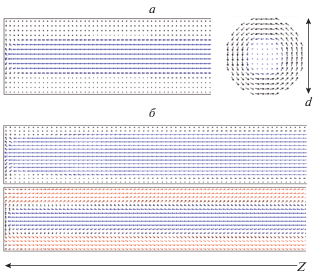
Приложение циркулярного магнитного поля (за счет пропускания электрического тока) к микропроводу с положительной магнитострикцией приводит к отклонению намагниченности в приповерхностной области в азимутальном направлении. В результате в области изменения преимущественного направления намагниченности образуются небольшие области с намагниченностью, противоположной по направлению намагниченности керна (рис. 3а). Тем не менее, эти структуры не стабильны во времени и не обеспечивают переключения намагниченности керна.

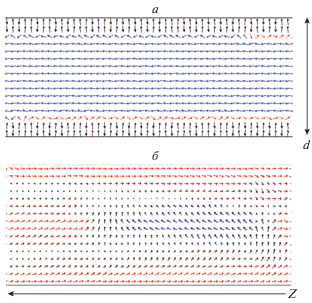
Для провода с отрицательной магнитострикцией изменение направления намагниченности в приповерхностной области также приводит к появлению области с намагниченностью, обратной по отношению к намагниченности осевого домена. Кроме того, при вариациях константы магнитоупругой анизотропии K_me наблюдалось переключение направления намагниченности в осевой области микропровода в случаях более слабой анизотропии (рис. 3б).

ЗАКЛЮЧЕНИЕ

Микромагнитное моделирование аморфных микропроводов с различными знаками магнитострикции было проведено с использованием пакета OOMMF. Полученные в результате моделирования распределения намагниченности соответствуют модели керн-оболочка. Изменения распределения намагниченности, вызванные однородным аксиальным магнитным полем, соответствуют экспериментальным данным о магнитных свойствах микропроводов. Моделирование токового перемагничивания микропроводов было проведено с учетом неоднородного распределения электрического тока и создаваемого им магнитного поля по сечению проводника. Полученные результаты подтвердили возможное переключение намагниченности керна микропровода с отрицательной магнитострикцией при пропускании переменного электрического тока.

Поскольку прямое наблюдение микромагнитной структуры с использованием доступных в настоящее время методов микротомографии невозможно, моделирование может предоставить новую информацию о зависимостях микромагнитной структуры от различных параметров, включая состав сплава, диаметр ферромагнитной жилы и толщину стеклянной оболочки. Таким образом, процесс перемагничивания может быть настроен путем варьирования параметров модели до экспериментальных доказательств.

Работа выполнена при поддержке РФФИ (проект № 19-32-90089).