Известия РАН. Серия физическая, 2022, T. 86, № 2, стр. 269-275
Прецизионные методы расчета нестационарных задач интегральной фотоники
А. А. Белов 1, 2, *, Ж. О. Домбровская 1
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный университет имени М.В. Ломоносова”, физический факультет
Москва, Россия
2 Федеральное государственное автономное образовательное учреждение высшего образования
“Российский университет дружбы народов”
Москва, Россия
* E-mail: aa.belov@physics.msu.ru
Поступила в редакцию 01.10.2021
После доработки 11.10.2021
Принята к публикации 22.10.2021
- EDN: EACFPD
- DOI: 10.31857/S0367676522020077
Аннотация
В слоистых средах решение уравнений Максвелла испытывает разрыв производной или самой функции на границах раздела сред. Впервые предложены конечно-разностные схемы, обеспечивающие сходимость разрывных решений. Это бикомпактные консервативные схемы. Они являются двухточечными, и границы слоев принимаются в качестве узлов сетки. Предложен принципиально новый способ учета дисперсии среды. Данные подходы обеспечивают второй порядок точности даже в случае разрывных решений.
ВВЕДЕНИЕ
В последние годы активно исследуются многослойные метапленки и фотонные кристаллы. Эти структуры представляют значительный интерес из-за новых физических явлений, присутствующих в их оптическом отклике (см., например, [1‒3]). Предполагается использовать такие структуры в качестве элементной базы для устройств интегральной фотоники (см. например, [4–7]). В них временной масштаб оптического отклика составляет десятки фемтосекунд. Любой натурный эксперимент предваряется численным моделированием. Для этого требуются высоконадежные и эффективные численные методы.
Многие подходы (например, матричные методы, методы конечных элементов, методы дискретных источников) дают хорошие результаты для достаточно узких классов задач. Наиболее универсальны разностные методы. Для них закрепилось общее название Finite-Difference Time Domain (FDTD) method [8]. Практически все они сводятся к схеме типа “крест” [9], в которой электрическое и магнитное поля относятся к целым и полуцелым пространственным узлам и временны́м слоям. Методам FDTD посвящено более 2000 работ, но принципиальные трудности этих методов не устранены.
Во-первых, в реальных задачах всегда присутствуют границы раздела, на которых поля испытывают слабый либо сильный разрыв. Схема “крест” в этом случае включает разностное дифференцирование через границу раздела. Поэтому точность катастрофически падает, а сходимость может вовсе отсутствовать. На практике разрыв показателя преломления сглаживают. Однако это сильно ослабляет расчетное отражение.
Во-вторых, показатель преломления актуальных материалов (Si, Ge и др.) зависит от частоты сложным образом. Схемы типа FDTD позволяют учитывать только простейшие модельные законы дисперсии (полиномиальный, модель Лоренца и некоторые другие) [10]. Реальные законы дисперсии приближенно описывают комбинацией модельных законов. Это также вносит существенную погрешность [11].
В данной работе предложена новая полностью консервативная разностная схема для системы одномерных уравнений Максвелла. Она основана на принципе бикомпактности [12, 13]. Шаблон схемы содержит только два соседних пространственных узла, а границы раздела сред располагаются в узлах сетки. При этом схема явно включает условия сопряжения во всех пространственных узлах. Поэтому она реализует законы сохранения для сеточных функций сетки. Предложенная схема обеспечивает второй порядок точности даже для разрывных решений. Такие схемы для уравнений Максвелла ранее не были известны.
Для нестационарных задач предложен принципиально новый метод спектрального разложения, позволяющий учитывать дисперсию материала. Закон дисперсии может быть произвольным (в том числе заданным таблично). Этот подход имеет простую физическую интерпретацию и строгое математическое обоснование. Он применим для других линейных гиперболических задач в дисперсионных средах.
Для верификации предложенных методов проведены расчеты задачи о нормальном падении плоской волны на одномерный фотонный кристалл. Предложена специальная процедура, названная методом виртуального эксперимента, которая позволяет учитывать неидеальность изготовления образца (т.е. флуктуации толщин слоев). Этот фактор существенно влияет на интерференцию отраженных волн внутри фотонного кристалла. Рассчитан спектр прохождения через фотонный кристалл, и проведено его сравнение с ранее измеренным. Эти спектры хорошо согласуются в пределах экспериментальных погрешностей 2–5%.
КОНСЕРВАТИВНОСТЬ
Уравнения математической физики выводятся из интегральных соотношений (уравнений баланса), выражающих законы сохранения для малого объема. Разностная схема должна отражать основные свойства сплошной среды. Важнейшим свойством является выполнение разностных аналогов основных законов сохранения. Такие схемы называются консервативными [14–17]. При этом уравнение баланса для всей расчетной области должно быть алгебраическим следствием балансов в отдельных ячейках. Для построения консервативных схем в [14–16] предложен интегро-интерполяционный метод.
В сложных задачах может быть несколько законов сохранения. Примером такой является газодинамика: одновременно должны выполняться законы сохранения массы, импульса и энергии. Схемы, выражающие все нужные законы сохранения, называются полностью консервативными. Для задач электродинамики исходными физическими законами сохранения являются интегральные уравнения Максвелла. Напомним, что эти законы выражают сохранение а) потока электрической индукции через замкнутую поверхность (закон Гаусса); б) потока магнитной индукции через замкнутую поверхность (закон Гаусса для магнитного поля); в) потока магнитной индукции через незамкнутую поверхность, натянутую на контур с током (закон Фарадея); г) потока электрической индукции через незамкнутую поверхность, натянутую на замкнутый контур, по которому вычисляется циркуляция напряженности магнитного поля (теорема о циркуляции).
Дифференциальные формы основных уравнений применимы только если решение является достаточно гладким. Если же решение имеет разрыв или излом, то в точке разрыва дифференциальное уравнение неприменимо. В этом случае записывают интегральные уравнения баланса для малого объема, захватывающего области по обе стороны от разрыва. Далее этот объем стягивают в точку, совпадающую с разрывом. Это дает условия на разрыве. Например, в газодинамике таковыми являются условия Гюгонио, определяющие скачок температуры и давления в ударной волне.
В электродинамике применение интегральных уравнений Максвелла к указанному объему дает известные условия сопряжения полей на границе раздела сред. Эти условия являются прямым следствием исходных уравнений баланса. Тем самым, чтобы схема для расчета электродинамики слоистых сред была полностью консервативной, она обязательно должна учитывать не только уравнения Максвелла внутри слоев, но и условия сопряжения на границах раздела. В противном случае возникает сеточный дисбаланс, который влияет на решение во всей области.
Например, в схеме Йе метода конечных разностей во временной области (FDTD) это приводит к появлению нефизичных осцилляций и резкому падению точности (порядок точности ухудшается до первого) [18]. Для этой схемы доказано, что для однородной среды из разностных роторных уравнений следует разностный аналог дивергентных [8]. Однако эта схема не учитывает физически корректных условий сопряжения на границах раздела. Поэтому она неконсервативна согласно указанному выше определению по Тихонову-Самарскому. То же относится и к другим конечно-разностным и конечно-элементным методам, не учитывающим условия сопряжения.
СТАЦИОНАРНАЯ ЗАДАЧА
Рассмотрим распространение плоской электромагнитной волны частоты $\omega $ перпендикулярно набору из $Q$ плоско-параллельных диэлектрических пластин общей толщиной a. Обозначим координаты границ слоев через ${{\xi }_{1}} \leqslant {{\xi }_{2}} \leqslant \ldots \leqslant {{\xi }_{{Q - 1}}}.$ Пусть объемные и поверхностные токи зависят от времени как $\sim {\kern 1pt} {{e}^{{ - i\omega t}}}.$
Направим ось $z$ перпендикулярно пластинам. Тогда электрическое поле $\vec {E}$ направлено по оси x, магнитное поле $\vec {H}$ – по оси $y$, волновой вектор $\vec {k}$ – по оси z. Здесь $k = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c},$ где $c$ – скорость света. Диэлектрическая проницаемость ${{\varepsilon }_{q}},$ магнитная восприимчивость ${{\mu }_{q}},$ проводимость ${{\sigma }_{q}},$ объемная плотность токов ${{\vec {J}}_{q}}$ q-й пластины, поверхностная плотность токов ${{\vec {j}}_{q}}$ на q-й границе не зависят от x и y. Вектора ${{\vec {J}}_{q}}$ и ${{\vec {j}}_{q}}$ направлены по оси x. Амплитуды полей зависят только от z. Такая задача описывается системой интегральных уравнений Максвелла
(1)
$\begin{gathered} \int\limits_\Gamma {{{H}_{q}}dl} = 4\pi {{c}^{{ - 1}}}\int\limits_S {({{J}_{q}} + {{\sigma }_{q}}{{E}_{q}})ds} + \\ + \,\,{{c}^{{ - 1}}}( - i\omega )\int\limits_S {{{D}_{q}}ds} ,\,\,\,\,{{D}_{q}} = {{\varepsilon }_{q}}{{E}_{q}}, \\ \int\limits_\Gamma {{{E}_{q}}dl} = - {{c}^{{ - 1}}}( - i\omega )\int\limits_S {{{B}_{q}}ds} ,\,\,\,\,{{B}_{q}} = {{\mu }_{k}}{{H}_{q}}. \\ \end{gathered} $(2)
$\begin{gathered} {{\partial }_{z}}{{E}_{1}} + i\omega {{c}^{{ - 1}}}{{E}_{1}} = 2ik{{E}^{0}},\,\,\,z = 0; \\ {{\partial }_{z}}{{E}_{Q}} - i\omega {{c}^{{ - 1}}}{{E}_{Q}} = 2ik{{E}^{a}}{{e}^{{ - ika}}},\,\,\,z = a. \\ \end{gathered} $(3)
$\begin{gathered} {{e}_{z}} \times ({{E}_{q}} - {{E}_{{q - 1}}}) = 0,\,\,\,{{e}_{z}}({{D}_{q}} - {{D}_{{q - 1}}}) = 0, \\ {{e}_{z}} \times ({{H}_{q}} - {{H}_{{q - 1}}}) = 4\pi {{c}^{{ - 1}}}{{j}_{q}},\,\,\,{{e}_{z}}({{B}_{q}} - {{B}_{{q - 1}}}) = 0. \\ \end{gathered} $Введем специальную сетку $\{ {{z}_{n}}\} ,$ $0 \leqslant n \leqslant N,$ $\Delta {{z}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{z}_{{n + 1}}} - {{z}_{n}},$ у которой границы слоев являются узлами. Составим линейную интерполяцию сеточных значений полей между узлами
(4)
$\begin{gathered} E(z) = {{\alpha }_{n}}z + {{\beta }_{n}},\,\,\,H(z) = {{\gamma }_{n}}z + {{\delta }_{n}},\,\,\,{{z}_{n}} \leqslant z \leqslant {{z}_{{n + 1}}}, \\ 0 \leqslant n \leqslant N - 1. \\ \end{gathered} $Здесь ${{\alpha }_{n}},$ ${{\beta }_{n}},$ ${{\gamma }_{n}},$ ${{\delta }_{n}}$ – коэффициенты интерполяции. Подставим интерполяцию (4) в задачу (1). При этом интегралы в (1) вычисляются по формуле трапеций, условия сопряжения аппроксимируются точно, а производные ${{\partial {{E}_{1}}} \mathord{\left/ {\vphantom {{\partial {{E}_{1}}} {\partial z}}} \right. \kern-0em} {\partial z}},$ ${{\partial {{E}_{Q}}} \mathord{\left/ {\vphantom {{\partial {{E}_{Q}}} {\partial z}}} \right. \kern-0em} {\partial z}}$ выразим из дифференциального уравнения Максвелла ${\text{rot}}{{E}_{q}} = i\omega {{c}^{{ - 1}}}{{\mu }_{q}}{{H}_{q}},$ записанного в узлах ${{z}_{0}}$ и ${{z}_{N}}$ соответственно. Это дает систему разностную схему для стационарной задачи
(5)
$\begin{gathered} {{\gamma }_{n}} = 4\pi {{c}^{{ - 1}}}{{J}_{q}}({{{\bar {z}}}_{n}}) - {{c}^{{ - 1}}}\left( {i\omega {{\varepsilon }_{q}}({{{\bar {z}}}_{n}}) - 4\pi {{\sigma }_{q}}({{{\bar {z}}}_{n}})} \right)({{\alpha }_{n}}{{{\bar {z}}}_{n}} + {{\beta }_{n}}); \\ {{\alpha }_{n}} = i\omega {{c}^{{ - 1}}}{{\mu }_{q}}({{{\bar {z}}}_{n}})({{\gamma }_{n}}{{{\bar {z}}}_{n}} + {{\delta }_{n}});\,\,\,\,{{\alpha }_{n}}{{z}_{{n + 1}}} + {{\beta }_{n}} = {{\alpha }_{{n + 1}}}{{z}_{{n + 1}}} + {{\beta }_{{n + 1}}}, \\ {{\gamma }_{{n + 1}}}{{z}_{{n + 1}}} + {{\delta }_{{n + 1}}} - {{\gamma }_{n}}{{z}_{{n + 1}}} - {{\delta }_{n}} = 4\pi {{c}^{{ - 1}}}j({{z}_{{n + 1}}}); \\ i\mu ({{{\bar {z}}}_{0}}){{\delta }_{0}} + i\sqrt {\varepsilon ({{{\bar {z}}}_{0}})\mu ({{{\bar {z}}}_{0}})} {{\beta }_{0}} = 2i\sqrt {\varepsilon ({{{\bar {z}}}_{0}})\mu ({{{\bar {z}}}_{0}})} {{E}^{0}}; \\ i\mu ({{{\bar {z}}}_{N}})({{\gamma }_{N}}a + {{\delta }_{N}}) - i\sqrt {\varepsilon ({{{\bar {z}}}_{N}})\mu ({{{\bar {z}}}_{N}})} ({{\alpha }_{N}}a + {{\beta }_{N}}) = 2i\sqrt {\varepsilon ({{{\bar {z}}}_{N}})\mu ({{{\bar {z}}}_{N}})} {{E}^{a}}. \\ \end{gathered} $Здесь ${{\bar {z}}_{n}} = 0.5({{z}_{n}} + {{z}_{{n + 1}}}).$ Схема (5) является принципиально новой. Шаблон схемы включает только один шаг по пространству, т.е. схема является бикомпактной. Поэтому при выборе специальных сеток не возникает дифференцирования через границу раздела. Справедлива
Теорема 1. Разностная схема (5) на специальных сетках сходится со вторым порядком точности.
Доказательство. Согласно классическим теоремам теории разностных схем [16], из аппроксимации и устойчивости схемы следует ее сходимость.
Обоснуем аппроксимацию схемы (5) . Пусть внутри q-й пластины величины $\varepsilon ,$ $\mu ,$ $J$ имеют вторые непрерывные производные по координате. Тогда решение может иметь разрывы только на границах раздела, и внутри пластин имеет третью непрерывную производную. Поэтому на специальных сетках линейная интереполяция (4) аппроксимирует решение с точностью $O(\Delta {{z}^{2}}).$ Тем самым, разностная схема (5) имеет 2-й порядок аппроксимации.
Обоснуем устойчивость схемы (5) . Пусть волна заданной амплитуды распространяется в однородной среде (для определенности, в сторону увеличения $z$), и в узле ${{z}_{n}}$ ее электрическое поле равно ${{E}_{n}}.$ Можно показать, что в узле ${{z}_{{n + 1}}} = {{z}_{{n + 1}}} + \Delta {{z}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ электрическое поле равно
(6)
${{E}_{{n + 1}}} = \frac{{1 + 0.5i\omega {{\Delta }_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{c}^{{ - 1}}}\sqrt {\varepsilon \mu } }}{{1 - 0.5i\omega {{\Delta }_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{c}^{{ - 1}}}\sqrt {\varepsilon \mu } }}{{E}_{n}}.$Для реальных физических сред, у которых $\operatorname{Re} \sqrt {\varepsilon \mu } \geqslant 1,$ $\operatorname{Im} \sqrt {\varepsilon \mu } \leqslant 0$ выполняется
(7)
$\left| {{{E}_{{n + 1}}}} \right| \leqslant \left| {{{E}_{n}}} \right|,\,\,\,\,\left| {{{H}_{{n + 1}}}} \right| \leqslant \left| {{{H}_{n}}} \right|.$Если волна распространяется в слоистой среде, и в соседнем интервале $\Delta {{z}_{{n + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$ материальные параметры отличаются от таковых в интервале $\Delta {{z}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ то неравенство (7) тем более выполняется из-за частичного отражения волны от границы раздела сред. Аналогично можно показать, что для волны, распространяющейся в сторону уменьшения z, имеют место неравенства
(8)
$\left| {{{E}_{{n + 1}}}} \right| \geqslant \left| {{{E}_{n}}} \right|,\,\,\,\,\left| {{{H}_{{n + 1}}}} \right| \geqslant \left| {{{H}_{n}}} \right|.$Граничные условия, объемные и поверхностные токи являются источниками волн, распространяющихся в обоих направлениях оси z. Из (7) и (8) следует, что амплитуда этих волн не нарастает по мере удаления от источника. Соответственно, не будут нарастать и малые ошибки $\delta ,$ внесенные в граничные условия, объемные и поверхностные токи. В силу линейности задачи справедлива оценка
где $C$ есть мажорирующая постоянная, не зависящая от шага сетки. Отсюда следует устойчивость схемы по граничным условиям и правым частям. Теорема доказана.Для схемы (5) применим метод сгущения сеток и оценки точности по методу Ричардсона [19–21]. В литературе предлагались различные методы локального сгущения и построения адаптивных сеток [22–24]. Однако эти подходы не дают оценок фактической точности. Напротив, глобальное сгущение сетки в методе Ричардсона дает апостериорную асимптотически точное значение погрешности. Этот подход является строго обоснованным [25].
Схема фактически построена интегро-интерполяционным методом. Поэтому для сред с непрерывно изменяющимися свойствами консервативность схемы следует из аддитивности интегралов. При наличии границ раздела консервативность обеспечивается явным учетом условий сопряжения. Таким образом, схема является полностью консервативной в смысле определения Тихонова–Самарского. Величины, сохраняемые схемой, перечислены выше.
Бикомпактность и полная консервативность обеспечивают сходимость численного решения к точному даже если последнее имеет сильные или слабые разрывы. Ранее известные схемы не обладали такими свойствами.
НЕСТАЦИОНАРНАЯ ЗАДАЧА
В постановке (1)–(3) заменим множитель $( - i\omega )$ на производную ${{\partial }_{t}}.$ Объемные ${{J}_{q}}(z,t)$ и поверхностные ${{j}_{q}}(z,t)$ токи могут произвольно зависеть от времени. Слева и справа на рассеиватель падают волновые пакеты ${{E}^{0}}(t)exp( - i\omega t),$ ${{E}^{a}}(t + {a \mathord{\left/ {\vphantom {a c}} \right. \kern-0em} c})exp( - i\omega t - ika)$ с несущей частотой $\omega $ и заданными огибающими ${{E}^{{0,a}}}.$
При распространении волнового пакета в линейной диспергирующей среде для каждой гармоники реализуются свои $\varepsilon ,$ $\mu ,$ $\sigma .$ Выполним численно преобразование Фурье падающих волновых пакетов, объемных и поверхностных токов по формуле трапеций, используя всюду одинаковые сетки по времени и наборы частот $\{ {{\omega }_{m}}\} ,$ ${{\omega }_{{m + 1}}} - {{\omega }_{m}} = \Delta {{\omega }_{m}}.$ Для каждой частоты получим свои амплитуды компонент падающих волновых пакетов $E_{m}^{{0,a}}$ и источников поля ${{({{J}_{q}})}_{m}},$ ${{({{j}_{q}})}_{m}}.$
Решим описанным выше методом набор стационарных задач, каждая из которых соответствует своей частоте ${{\omega }_{m}}.$ Полученные амплитуды просуммируем по всем частотам ${{\omega }_{m}}.$ Это и даст решение нестационарной задачи $E(z,t),$ $H(z,t).$ Это принципиально новый подход. Он был назван методом спектрального разложения. Имеет место
Теорема 2. Схема метода спектрального разложения сходится со вторым порядком точности.
Доказательство. Если функции ${{E}^{{0,a}}},$ ${{J}_{q}},$ ${{j}_{q}}$ имеют вторые непрерывные производные, то формула трапеций обеспечивает 2-й порядок аппроксимации для прямого и обратного преобразований Фурье.
Обоснуем устойчивость метода. Заметим, что в реальных задачах падающие импульсы и токи являются локализованными функциями времени. Длину промежутка времени, на котором они отличны от нуля, обозначим через T. Фурье-образы этих функций также являются локализованными. Интервал частот, на котором они отличны от нуля, обозначим через $\Omega .$
Пусть в одну из функций ${{E}^{{0,a}}},$ ${{J}_{q}},$ ${{j}_{q}}$ внесена малая ошибка $\delta .$ Тогда ошибка соответствующего фурье-образа не превосходит ${{\delta }_{\omega }} \leqslant {{(2\pi )}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}T\max \left| \delta \right|.$ Последняя величина есть ошибка входных данных каждой из стационарных задач. Из (9) следует, что соответствующие погрешности решений стационарных задач не превосходят $\left| {\delta {{E}_{\omega }}} \right|,$ $\left| {\delta {{H}_{\omega }}} \right| \leqslant C{{(2\pi )}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}T\max \left| \delta \right|.$ Тогда итоговая погрешность решения нестационарной задачи не превосходит $\left| {\delta E} \right|,\left| {\delta H} \right| \leqslant C{{(2\pi )}^{{ - 1}}}T\Omega \max \left| \delta \right|.$ Поэтому метод устойчив относительно малых возмущений входных данных. По классическим теоремам, отсюда следует сходимость схемы метода спектрального разложения. Теорема доказана.
Для предлагаемого метода применимы оценки погрешности по методу Ричардсона и экстраполяционное уточнение. Заметим, что сетки по z, t, $\omega $ должны сгущаться одновременно и в одинаковое число раз.
Несмотря на свою простоту, метод спектрального разложения является принципиально новым. Он позволяет учитывать произвольный закон дисперсии (в том числе заданный в виде таблицы). Этот подход рекомендуется в качестве общего метода построения разностных схем для гиперболических задач в линейной дисперсионной среде.
АПРОБАЦИЯ МЕТОДА
Фотонный кристалл
Наиболее представительной проверкой любого численного метода является расчет реальной задачи и сравнение с результатами эксперимента. В качестве примера рассмотрим распространение излучения через одномерный фотонный кристалл (ФК) при нормальном падении.
Пусть ФК состоит из 7 пар слоев (SiO2 – 160 нм, Ta2O5 – 112 нм). Поверх последнего слоя Ta2O5 нанесен слой SiO2 толщиной 260 нм (см. рис. 1) [26]. ФК находится в воздухе. Зависимость диэлектрических проницаемостей этих материалов от длины волны, предоставленная производителем [27], показана на рис. 2. Для этого ФК производитель предоставил экспериментально измеренные спектры пропускания при нормальном падении [27] (см. рис. 3).
Рис. 1.
Фотонный кристалл. Зависимость $\varepsilon $ при длине волны $\lambda = 900$ нм от координаты z. Вертикальные линии – границы слоев.
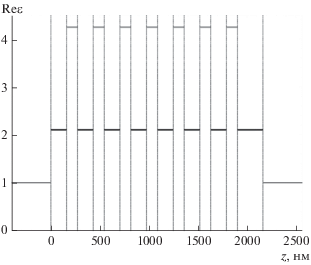
Рис. 2.
Зависимость материальных параметров от длины волны. Пунктирная линия – $\operatorname{Re} \varepsilon $ для SiO2, сплошная линия – $\operatorname{Re} \varepsilon $ для Ta2O5, пунктирная линия – ${{10}^{3}}\operatorname{Im} \varepsilon $ для Ta2O5.
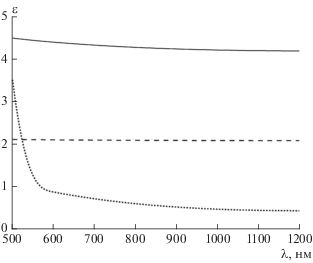
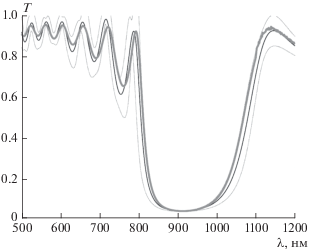
Рис. 3.
Спектр прохождения ФК. Жирная линия – эксперимент [27]. Тонкая линия – расчет. Пунктирные линии – границы доверительного интервала, полученные методом виртуального эксперимента (двум стандартным отклонениям).
Виртуальный эксперимент
Изготовление оптических наноструктур – сложный технологический процесс. Из-за этого геометрические параметры рассеивателя (например, толщины слоев ФК) могут флуктуировать. Эти флуктуации составляют несколько процентов от размера рассеивателя. Они вносят существенные искажения в электромагнитный отклик конструкции. Например, колебания толщины слоя ФК влияют на интерференцию отраженных волн внутри ФК. Это приводит к размытию резких минимумов и максимумов в спектрах отражения и пропускания. Физическая природа этого фактора известна [28], однако универсальная процедура расчета не разработана.
Мы используем метод виртуального эксперимента [29]. Пусть один из параметров задачи $A$ известен с ошибкой σA. Будем считать этот параметр нормально распределенной случайной величиной с математическим ожиданием $A$ и стандартным отклонением ${{\sigma }_{A}}.$ Электромагнитный отклик структуры является функцией этой случайной величины. Поэтому результаты расчета необходимо усреднить по распределению значения A. Одновременно можно найти доверительный интервал, т.е. оценку погрешности, вносимую погрешностью задания величины A.
В случае неидеального ФК $A$ – это вектор, содержащий толщины всех слоев. Функция распределения этого вектора есть произведение соответствующего числа одномерных гауссовых распределений. В задачах нанофотоники этот подход ранее не использовался.
Результаты моделирования
На рис. 3 показан рассчитанный спектр прохождения через рассматриваемый ФК при нормальном падении. В расчетах учитывались колебания толщины с типичным значением ±4.5 нм для всех слоев ФК. Это согласуется с известными оценками, полученными с помощью эллипсометрии. Для расчетной кривой представлен доверительный интервал, то есть оценка погрешности из-за неточности задания толщин слоев. Эта оценка была получена с помощью виртуального эксперимента и соответствует двум стандартным отклонениям.
Заметим, что данный расчет проверяет метод виртуального эксперимента и стационарную бикомпактную схему для каждой частоты. В этом случае также применимы матричные методы. Однако конечно-разностные методы более универсальны и, в отличие от матричных методов, могут быть обобщены на многомерный случай. Такое обобщение выходит за рамки настоящей работы.
Видно, что спектр, рассчитанный по бикомпактной схеме и методу виртуального эксперимента, согласуется с экспериментальным спектром в пределах 2–5% в широком диапазоне длин волн 500–1200 нм. Это соответствует точности самого эксперимента. Также видно, что ширина доверительного интервала по методу виртуального эксперимента сопоставима с расхождением расчетного и экспериментального спектров. Поэтому флуктуации толщин слоев ФК являются важным фактором, и их необходимо учитывать в расчетах.
ЗАКЛЮЧЕНИЕ
Предложенные методы обеспечивают высокую количественную точность расчета реальных нестационарных задач фотоники. Это особенно важно при численных исследованиях сложных эффектов, таких как долгоживущие связанные состояния (поверхностные волны различных типов), а также при разработке новых устройств интегральной фотоники.
Работа выполнена при поддержке Российского научного фонда (проект № 20-71-00097).
Список литературы
Ropers C., Park D.J., Stibenz G. et al. // Phys. Rev. Lett. 2005. V. 94. Art. No. 113901.
Afinogenov B.I., Popkova A.A., Bessonov V.O., Fedya-nin A.A. // Appl. Phys. Lett. 2016. V. 141. Art. No. 171107.
Afinogenov B.I., Bessonov V.O., Soboleva I.V., Fedyanin A.A. // ACS Photon. 2019. V. 6. No. 4. P. 844.
Bruckner R., Zakhidov A.A., Scholz R. et al. // Nature Photon. 2012. V. 6. P. 322.
Symonds C., Lheureux G., Hugonin J.P. et al. // Nano Lett. 2013. V. 13. No. 7. P. 3179.
Das R., Srivastava T., Jha R. // Opt. Lett. 2014. V. 39. No. 4. P. 896.
Badugu R., Lakowicz J.R. // J. Phys. Chem. C. 2014. V. 118. No. 37. Art. No. 21558.
Inan U.S., Marshall R.A. Numerical electromagnetics. The FDTD method. Cambridge: Cambridge Univ. Press, 2011.
Yee K. // IEEE Trans. Antennas. Propag. 1966. V. 14. No. 3. P. 302.
Sullivan D.M. Electromagnetic simulation using the FDTD method. IEEE Press, 2000.
Petropoulos P.G. // IEEE Trans. Antennas Propag. 1994. V. 42. No. 1. P. 62.
Kalitkin N.N., Koryakin P.V. // Dokl. Math. 2008. V. 77. P. 320
Kalitkin N.N., Koryakin P.V. // Math. Mod. Comp. Simul. 2010. V. 2. No. 2. P. 139.
Tikhonov A.N., Samarskii A.A. // Rep. Acad. Sci. USSR. 1959. V. 8. No. 3. P. 529.
Самарский А.А. Введение в теорию разностных схем. М.: Наука, гл. ред. физ.-мат. лит., 1971. 553 с.
Самарский А.А. Теория разностных схем. М.: Наука, гл. ред. физ.-мат. лит., 1977. 656 с.
Samarskii A.A. The theory of difference schemes. M.: Nauka, 1979.
Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М.: Наука, гл. ред. физ.-мат. лит., 1992. 424 с.
Dombrovskaya Zh.O., Belov A.A. // J. Phys. Conf. Ser. 2020. V. 1461. Art. No. 012032.
Richardson L.F., Gaunt A. // Phil. Trans. Royal Soc. A. 1927. V. 226. No. 636–646. P. 299.
Марчук Г.И., Шайдуров В.В. Повышение точности решений разностных схем. М.: Наука, гл. ред. физ.-мат. лит., 1979. 320 с.
Калиткин Н.Н., Альшин А.Б., Альшина Е.А., Рогов Б.В. Вычисления на квазиравномерных сетках. М.: Физматлит, 2005. 224 с.
Meglicki Z., Gray S.K., Norris B. // Comp. Phys. Commun. 2007. V. 176. P. 109.
Van Londersele A., De Zutter D., Ginste D.V. // J. Comp. Phys. 2017. V. 342. P. 177.
Balsara D.S., Simpson J.J. // J. Multisc. Multiphys. Comp. Techniq. 2020. V. 5. P. 99.
Рябенький В.С., Филиппов А.Ф. Об устойчивости разностных уравнений. М.: Гостехиздат, 1956. 171 с.
Popkova A.A., Chezhegov A.A., Soboleva I.V. et al. // J. Phys. Conf. Ser. 2020. V. 1461. Art. No. 012134.
http://www.izovac-coatings.com/en.
Taflove A., Hagness S.C. Computational electrodynamics: The finite-difference time-domain method. London: Artech House, 2005.
Belov A.A., Kalitkin N.N., Kozlitin I.A. // Fus. Eng. Des. 2019. V. 141. P. 51.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


