Известия РАН. Серия физическая, 2022, T. 86, № 2, стр. 234-241

ВВЕДЕНИЕ

В последние годы нанотехнологии, основанные на сочетании оптики и плазмоники, формируют новый сценарий развития телекоммуникационной и компьютерной техники. Плазмонные наноустройства на основе линейных и нелинейных эффектов способны воспроизводить большое количество функций полупроводниковых электронных устройств при малых размерах [1–6]. В связи с этим применение поверхностных плазмон-поляритонных волн становится все более и более востребованным благодаря их универсальным свойствам трансляции сигналов на оптических частотах.

Поверхностные плазмон-поляритоны (ППП) при линейном и нелинейном отклике сред генерируются в результате воздействия высокочастотного электромагнитного поля, падающего на границу раздела сред, на которой имеются неоднородности в форме щелей, либо возбуждаются электромагнитным полем с помощью диэлектрических призм [1, 2, 7]. Электромагнитное поле вызывает осцилляции как свободных, так и связанных зарядов в диэлектрических, полупроводниковых и металлических средах. При этом токи проводимости в объеме и на границах сред не возникают. Это позволяет генерировать ППП на оптических частотах, что существенно расширяет полосу передачи сигналов в плазмонных устройствах [5]. Помимо этого, длина волны ППП в композитной структуре может быть в несколько раз короче, чем длина оптической волны в воздухе или в оптическом волноводе.

Интенсивный сигнал – электромагнитная волна или мощный электромагнитный импульс, генерируют нелинейные плазмон-поляритонные волны – кноидальные волны, а также уединенные волны – солитоны, на границе раздела проводящей и диэлектрической сред [4, 8–13], в плазмонных волноводах [14–20], в металлических пленках [21] и наноструктурах [22] в результате самомодуляции волн из-за керровской нелинейности сред. Диэлектрические и магнитные проницаемости обеих сред в этом случае зависят от плотности энергии волны, то есть параметры и динамика плазмонных кноидальных волн и солитонов зависят от интенсивности возбуждающих электромагнитных волн и импульсов, а также от свойств сред и от геометрии волновода, в которых распространяются плазмон-поляритоны. В зависимости от мощности возбуждающего сигнала в случае возникновения нелинейного отклика плазмонной структуры, в том числе, при насыщении нелинейности [11], обусловленной электронными межзонными переходами при оптическим термоэффекте [23], меняется период кноидальной волны и форма импульсов [4, 12, 19], распространяющихся по границе раздела сред или по плазмонному волноводу.

В данной работе на основе полученной системы нелинейных уравнений для электрических компонент поперечной магнитной (ТМ) моды рассматривается динамика нелинейных волн и импульсов в потоке ППП, распространяющегося вдоль границы аморфной диэлектрической среды и металла. В системе уравнений учтено насыщение нелинейности среды и потери. Полученные в движущейся системе координат численные и аналитические решения нелинейной системы уравнений позволяют сравнить динамику нелинейных поверхностных плазмон-поляритонов (НППП) при возбуждении монохроматическим непрерывным и импульсным мощными электромагнитными сигналами. Анализ решений уравнений дает возможность предсказать поведение возбуждений в потоке НППП с учетом начальных и граничных условий, которые зависят от вида и мощности возбуждающего электромагнитного сигнала. Анализ динамики НППП, возбуждаемых в плазмонных волноводах электромагнитными сигналами различной мощности, необходим для проектирования устройств современной плазмонной техники, работающих на оптических частотах.

НЕЛИНЕЙНЫЕ МОДЫ ПОВЕРХНОСТНЫХ ПЛАЗМОН-ПОЛЯРИТОНОВ

Полагаем, что эванесцентная волна НППП распространяется на границе раздела диэлектрической среды и металла вдоль оси z, а ее амплитуда экспоненциально убывает при удалении от границы раздела сред вдоль нормальной к границе оси $x$ как $\sim {\kern 1pt} \exp ( - {{{{\alpha }}}_{D}}x)$ в положительном направлении $x > 0$ (в диэлектрике), и в отрицательном направлении $x < 0$ (в металле) $\sim {\kern 1pt} \exp ({{{{\alpha }}}_{M}}x),$ причем ${\text{Re}}{{{{\alpha }}}_{D}} > 0,$ ${\text{Re}}{{{{\alpha }}}_{M}} > 0$ (индексы D и M). Плотность энергии, пропорциональная квадрату напряженности электрического поля НППП $\sim {\kern 1pt} {{E}^{2}},$ зависит от нормальной к границе координаты как ${\text{exp}}\left( { - 2{{{{\alpha }}}_{D}}x} \right)$ и ${\text{exp}}\left( {2{{{{\alpha }}}_{M}}x} \right),$ поэтому энергия сосредоточена в тонком приграничном слое, причем НППП не излучаются с гладкой границы.

Полагаем, что для НППП с плоским волновым фронтом на границе раздела однородных немагнитных сред ${{{{\mu }}}_{D}} = 1,$ ${{{{\mu }}}_{M}} = 1$ с различными и диэлектрическими ${{{{\varepsilon }}}_{D}}$ и ${{{{\varepsilon }}}_{M}}$ проницаемостями компоненты поля не меняются вдоль поперечной оси y, то есть ${\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0em} {\partial y}} \to 0.$ Из уравнений Максвелла $\nabla \times \vec {H} = {{{{c}^{{ - 1}}}\partial \left( {{{\varepsilon }}\vec {E}} \right)} \mathord{\left/ {\vphantom {{{{c}^{{ - 1}}}\partial \left( {{{\varepsilon }}\vec {E}} \right)} {\partial t}}} \right. \kern-0em} {\partial t}},$ $\nabla \times \vec {E} = {{ - {{c}^{{ - 1}}}\partial \left( {{{\mu }}\vec {H}} \right)} \mathord{\left/ {\vphantom {{ - {{c}^{{ - 1}}}\partial \left( {{{\mu }}\vec {H}} \right)} {\partial t}}} \right. \kern-0em} {\partial t}}$ для немагнитных сред (${{\mu }} = 1$) получаем систему уравнений для компонент ТМ-волны (E_x, E_z, H_y) НППП в декартовой системе координат

где $\varepsilon \left( {t,z} \right) = {{\varepsilon }_{L}}\, + \chi {\kern 1pt} \left( {E_{x}^{*}{{E}_{x}}\, + E_{z}^{*}{{E}_{z}}} \right),$ ${{\varepsilon }_{L}}$ – диэлектрическая проницаемость среды, $\chi \, \equiv {{\chi }^{{\left( 3 \right)}}}\, = \left( {4\pi {{\chi }_{D}},4\pi {{\chi }_{M}}} \right)$ – восприимчивости третьего порядка диэлектрической аморфной среды и металла. В системе уравнений (1) поперечный коэффициент затухания НППП обозначен $\alpha .$ В систему уравнений (1) для диэлектрика должно быть подставлено значение $ - {{\alpha }_{D}},$ а для металла ${{\alpha }_{M}}.$ Коэффициенты затухания удовлетворяют уравнениям ${{\alpha }^{2}} = Re\beta _{L}^{2}$ – ${{{{\varepsilon }_{L}}{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{L}}{{\omega }^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}},$ где ${{\varepsilon }_{L}} = {{\varepsilon }_{D}}$ для диэлектрика, ${{\varepsilon }_{L}} = {{\varepsilon }_{M}}$ для металла; $\beta _{L}^{2}$ = ${{\left( {{{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} \right){{\varepsilon }_{D}}{{\varepsilon }_{M}}} \mathord{\left/ {\vphantom {{\left( {{{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} \right){{\varepsilon }_{D}}{{\varepsilon }_{M}}} {\left( {{{\varepsilon }_{D}} + {{\varepsilon }_{M}}} \right)}}} \right. \kern-0em} {\left( {{{\varepsilon }_{D}} + {{\varepsilon }_{M}}} \right)}}$ – квадрат постоянной распространения ППП в линейном режиме.

МОНОХРОМАТИЧЕСКИЙ НЕПРЕРЫВНЫЙ ВОЗБУЖДАЮЩИЙ СИГНАЛ

Монохроматический непрерывный электромагнитный сигнал ${{E}_{{ax}}}{\text{exp}}\left( { - i\omega t} \right),$ ${{E}_{{az}}}{\text{exp}}\left( { - i\omega t} \right),$ где ${{E}_{{ax}}} = {\text{const}},$ ${{E}_{{az}}} = {\text{const}},$ в линейном режиме при $\chi {{E}^{2}} \to 0$ на границе диэлектрика и металла возбуждает гармоническую волну ППП с компонентами электрического вектора ${{E}_{x}} = {{E}_{{ax}}}$${\text{exp}}\left[ { - i\omega \left( {t - {z \mathord{\left/ {\vphantom {z \nu }} \right. \kern-0em} \nu }} \right)} \right]$ и ${{E}_{x}} = {{E}_{{ax}}}$${\text{exp}}\left[ { - i\omega \left( {t - {z \mathord{\left/ {\vphantom {z \nu }} \right. \kern-0em} \nu }} \right)} \right],$ движущуюся со скоростью $\nu = {c \mathord{\left/ {\vphantom {c {{{n}_{f}}}}} \right. \kern-0em} {{{n}_{f}}}} = {\text{const}},$ где ${{n}_{f}}$ = ${{\left[ {{{\varepsilon }_{L}} + {{{{\alpha }^{2}}{{c}^{2}}} \mathord{\left/ {\vphantom {{{{\alpha }^{2}}{{c}^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$

Полагаем, что в нелинейном режиме $\chi {{E}^{2}} \ne 0$ монохроматический непрерывный сигнал на границе возбуждает волну НППП с электрическими компонентами ${{E}_{x}},~{{E}_{z}}~\sim {\text{exp}}\left( { - i\omega t} \right).$ Если нелинейная диэлектрическая проницаемость среды $\varepsilon \left( z \right) = {{\varepsilon }_{L}}$ + $\chi \left( {E_{x}^{*}{{E}_{x}} + E_{z}^{*}{{E}_{z}}} \right)$ не зависит от времени t, то система уравнений (1) для электрических компонент нелинейной ТМ-моды НППП приобретает вид [12, 19]

где насыщение нелинейности описывается слагаемым $\sim {\kern 1pt} \frac{1}{\varepsilon }\frac{{\partial \varepsilon }}{{\partial z}}{{E}_{z}}.$

Хорошо известно, что плоская нелинейная волна в среде неустойчива [24]. В средах под влиянием керровской нелинейности при увеличении амплитуды возбуждающего сигнала возникает самомодуляция волны НППП, что представлено на рис. 1. Из анализа динамики компонент электрического поля ТМ-моды НППП (рис. 1) следует, что при увеличении амплитуды возбуждающей электромагнитной волны эффективная длина волны НППП $\lambda = \frac{{2\pi }}{{{\text{Re}}\beta }},$ уменьшается, так как зависит от плотности энергии поля [19]. Мнимая часть компоненты электрического вектора, описывающая затухание НППП (рис. 1(c), рис. 1(d)), которая возбуждается при распространении НППП вдоль границы сред, находится в противофазе по отношению к действительной части компоненты (рис. 1(a), рис. 1(b)). Динамика компонент ${{E}_{x}}$ и ${{E}_{z}}$ совпадет, при этом величины амплитуд компонент относятся как ${{{{E}_{{ax}}}} \mathord{\left/ {\vphantom {{{{E}_{{ax}}}} {{{E}_{{az}}}}}} \right. \kern-0em} {{{E}_{{az}}}}} = {{{\text{Re}}\beta } \mathord{\left/ {\vphantom {{{\text{Re}}\beta } \alpha }} \right. \kern-0em} \alpha }.$

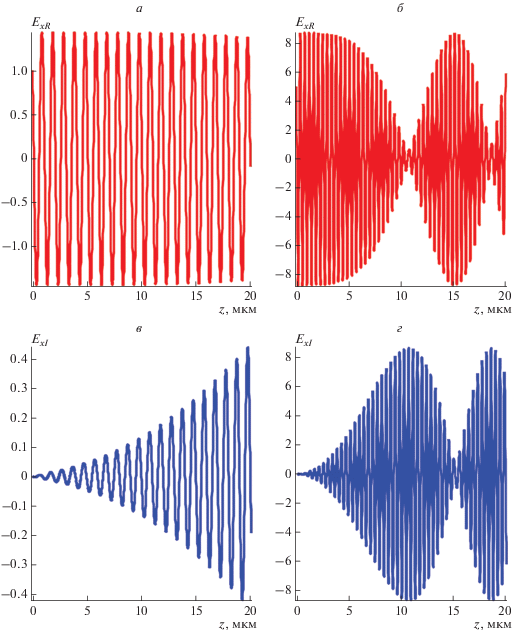
Расчет проводился для значений нелинейной диэлектрической восприимчивости среды ${\text{Re}}\chi > 0,$ $Im\chi = 0,$ которые характерны для диэлектрических сред в оптическом диапазоне. Для металлов, например, золота, в диапазоне длин волн электромагнитного возбуждающего сигнала 350–750 нм действительная и мнимая части нелинейной диэлектрической восприимчивости меняют величину и знаки от отрицательных до положительных значений, а при дальнейшем увеличении длины волны стремятся к нулю [23]. Это должно быть учтено при расчетах с помощью системы уравнений (2) для конкретной длины волны возбуждающего сигнала. Поэтому результаты модельных расчетов, представленные на рис. 1, характеризуют НППП в телекоммуникационном диапазоне (более 800 нм), в котором нелинейный отклик металлов практически равен нулю. Максимальная модельная величина нелинейного отклика $\chi {{E}^{2}}\left( 0 \right) = 1.0,$ используемая в расчетах, характерна для диэлектрических сред с ${{\chi }^{{\left( 3 \right)}}} = 4\pi {{\chi }_{D}}$ ~ ~ ${{10}^{{ - 18}}} \ldots ~{{10}^{{ - 20}}}\,\,{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{В}}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{В}}}^{{\text{2}}}}}}$ (типа халькогенидных стекол) [14], применимых для изоляции металлических волноводов в плазмонных микросхемах. Отсутствии разрушений в изоляторах при напряженности электрического поля $\sim {\kern 1pt} {{10}^{{10}}}\,\,{{\text{В}} \mathord{\left/ {\vphantom {{\text{В}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ имеет место для коротких импульсов. Поэтому проанализируем динамику НППП при возбуждении коротким импульсом и сравним с поведением НППП при возбуждении непрерывным сигналом.

ИМПУЛЬСНЫЙ ВОЗБУЖДАЮЩИЙ СИГНАЛ

При возбуждении НППП импульсным сигналом нелинейная проницаемость диэлектрической среды $\varepsilon \left( {t,z} \right)$ зависит от времени и продольной координаты, причем также имеет место насыщение нелинейности. В системе отсчета “движущаяся координата” $Z = z - \nu t,$ где $\nu = {c \mathord{\left/ {\vphantom {c {{{n}_{f}}}}} \right. \kern-0em} {{{n}_{f}}}} = {\text{const}}$ – скорость несущей волны волнового пакета, система уравнений (1) для компонент электрического поля НППП имеет вид

где $\varepsilon \left( Z \right) = {{\varepsilon }_{L}} + \chi {{E}^{2}},$ ${{E}^{2}} = E_{x}^{*}{{E}_{x}} + E_{z}^{*}{{E}_{z}},$ ${{n}_{f}}$ = = ${{\left[ {{{\varepsilon }_{L}} + {{{{\alpha }^{2}}{{c}^{2}}} \mathord{\left/ {\vphantom {{{{\alpha }^{2}}{{c}^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ В движущейся системе отсчета в системе уравнений (3) возникают множители $\frac{1}{{\varepsilon - n_{f}^{2}}},$ которые приводят к сингулярности поля ${{E}_{{x,z}}} \to \infty $ при $\chi {{E}^{2}} \to \frac{{{{\alpha }^{2}}{{c}^{2}}}}{{{{\omega }^{2}}}},$ что обусловлено переходом в движущуюся систему координат.

Если пренебречь насыщением нелинейности, полагая $\left| {\frac{{d{{E}_{x}}}}{{dZ}}} \right| \gg $$\left| {\frac{1}{{\varepsilon - n_{f}^{2}}}\frac{{d\varepsilon }}{{dZ}}{{E}_{x}}} \right|$ и $\left| {\frac{{d{{E}_{z}}}}{{dZ}}} \right| \gg $ $\left| {\frac{1}{\varepsilon }\frac{{d\varepsilon }}{{dZ}}{{E}_{z}}} \right|$ вдали от сингулярности, то, взяв вторые производные по Z в уравнениях (3) и комбинируя эти уравнения с уравнения с первыми производными, систему уравнений (3) можно упростить. Разлагая множитель $\frac{{\alpha n_{f}^{2}}}{{\varepsilon - n_{f}^{2}}}$ в ряд Тейлора по малому параметру $\chi {{E}^{2}} \ll 1,$ получаем систему нелинейных уравнений для электрических компонент НППП в рассматриваемом случае относительно низкой интенсивности НППП

где $\beta _{L}^{2} = \frac{{{{\omega }^{2}}{{\varepsilon }_{L}}}}{{{{c}^{2}}}} + {{\alpha }^{2}},$ $\bar {\chi } = \chi \frac{{{{\omega }^{2}}}}{{{{c}^{2}}{{\alpha }^{2}}}}.$ Из уравнений (4) следует, что эффективная длина волны НППП $\lambda = \frac{{2\pi }}{{{{\beta }_{L}}{{{\left( {1 + \bar {\chi }{{E}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}$ зависит от плотности энергии поля $\sim {\kern 1pt} {{E}^{2}}.$

Динамика компонент электрического поля E_x и ${{E}_{z}}$ короткого импульса НППП ${{E}_{{ax}}} = {\text{const}},$ ${{E}_{{az}}} = {\text{const}}$ без учета насыщения нелинейности, но с учетом затухания компонент электрического поля НППП, при значениях параметров, совпадающих с выбранными для непрерывного возбуждающего сигнала в нелинейном режиме, представлена на рис. 2. Из рис. 2 следует, что при возбуждении импульсным сигналом модуляция потока НППП происходит при меньших значениях амплитуд электрического поля, чем при возбуждении непрерывным сигналом (рис. 1) при тех же значениях остальных параметров.

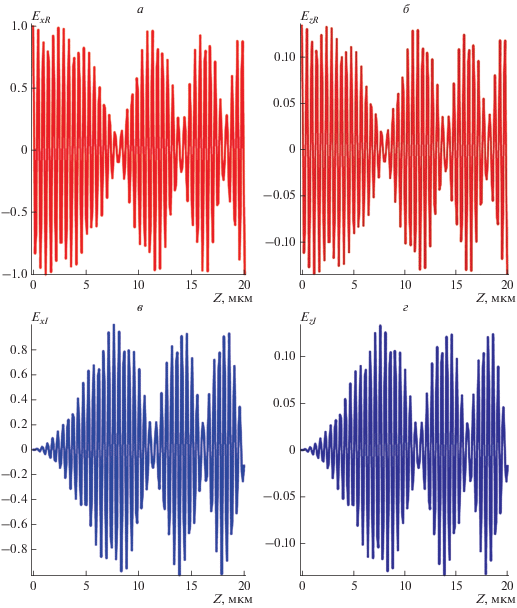
При относительно низкой интенсивности возбуждающего импульсного сигнала в системе отсчета “запаздывающее время” $\tau = t - {z \mathord{\left/ {\vphantom {z {\tilde {\nu }}}} \right. \kern-0em} {\tilde {\nu }}},$ где $\tilde {\nu } = {\text{const}},$ можно получить аналитические решения системы нелинейных уравнений, описывающих динамику импульса НППП. Система уравнений (1) для компонент электрического поля волнового пакета НППП в движущейся системе отсчета приобретает вид

где $\varepsilon \left( \tau \right) = {{\varepsilon }_{L}} + \chi \left( {E_{x}^{*}{{E}_{x}} + E_{z}^{*}{{E}_{z}}} \right).$ В случае низкой интенсивности НППП $\chi {{E}^{2}} \ll 1,$ пренебрегая насыщением нелинейности, получаем систему уравнений для компонент электрического поля в виде где ${{{{\Omega }}}^{2}} = \frac{{{{\alpha }^{2}}{{с}^{2}}}}{{{{\varepsilon }_{L}} - n_{f}^{2}}},$ $\tilde {\chi } = \frac{\chi }{{{{\varepsilon }_{L}} - n_{f}^{2}}}.$

Аналитическое решение системы нелинейных уравнений (6) можно найти [25], если представить ее в форме двух уравнений движения $\frac{{{{d}^{2}}{{E}_{x}}}}{{d{{\tau }^{2}}}} = - \frac{{\partial U}}{{\partial {{E}_{x}}}}$ и $\frac{{{{d}^{2}}{{E}_{z}}}}{{d{{\tau }^{2}}}} = - \frac{{\partial U}}{{\partial {{E}_{z}}}},$ где U = = $\frac{1}{2}{{{{\Omega }}}^{2}}\left[ {E_{x}^{2} + E_{z}^{2}\frac{{}}{{}}} \right.$ – $\left. {\frac{1}{2}\tilde {\chi }{{{\left( {E_{x}^{2} + E_{z}^{2}} \right)}}^{2}}} \right],$ или в форме векторного уравнения

где $\vec {E} = {{\vec {1}}_{x}}{{E}_{x}} + {{\vec {1}}_{z}}{{E}_{z}}.$ Электрический вектор $\vec {E}$ вращается в нормальной к границе раздела сред плоскости $\left( {x,z} \right).$ Учитывая, что ${\partial \mathord{\left/ {\vphantom {\partial {\partial{ \vec {E}}}}} \right. \kern-0em} {\partial{ \vec {E}}}} \to {{\left( {{{\partial \tau } \mathord{\left/ {\vphantom {{\partial \tau } {\partial{ \vec {E}}}}} \right. \kern-0em} {\partial{ \vec {E}}}}} \right)d} \mathord{\left/ {\vphantom {{\left( {{{\partial \tau } \mathord{\left/ {\vphantom {{\partial \tau } {\partial{ \vec {E}}}}} \right. \kern-0em} {\partial{ \vec {E}}}}} \right)d} {d\tau }}} \right. \kern-0em} {d\tau }},$ получаем первый интеграл уравнения (7)

Уравнение (8) в движущейся системе отсчета совпадает с уравнением для закона сохранения энергии $\tilde {E}$ материальной точки с единичной массой, движущейся по плоской траектории в центральном поле.

Решение нелинейного уравнения (8) представим в виде $\vec {E} = E\left( {{{{\vec {1}}}_{x}}{\text{cos}}\varphi + {{{\vec {1}}}_{z}}{\text{sin}}\varphi } \right),$ где $E\left( \tau \right)$ – модуль электрического вектора, $\varphi = \varphi \left( \tau \right)$ – циклическая координата (фаза). Тогда уравнение (8) приобретает вид

Уравнение (9) можно представить в форме уравнений Гамильтона $\frac{{\partial {{p}_{E}}}}{{\partial \tau }} = - \frac{{\partial{ \tilde {H}}}}{{\partial E}},$ $\frac{{\partial {{p}_{\varphi }}}}{{\partial \tau }} = \frac{{\partial{ \tilde {H}}}}{{\partial \varphi }} = 0,$ с функцией $\tilde {H} = \frac{1}{2}\left( {p_{E}^{2} + \frac{1}{{{{E}^{2}}}}p_{\varphi }^{2}} \right) + U,$ где ${{p}_{E}} = \frac{{dE}}{{d\tau }}$ и ${{p}_{\varphi }} = {{E}^{2}}\frac{{d\varphi }}{{d\tau }}$ – обобщенные импульсы [26]. Из второго уравнения Гамильтона следует, что азимутальный импульс ${{p}_{\varphi }} = \tilde {P} = {\text{const}}$ является интегралом движения. Тогда уравнение (9) представим в форме двух уравнений для переменных E и $\varphi ,$

Амплитуда электрического вектора НППП на границе раздела диэлектрика и металла определяется выражением $E = {{\left[ {\frac{{{{a}_{3}} - {{a}_{2}}{\text{s}}{{{\text{n}}}^{2}}\left( {\bar {\tau },\tilde {k}} \right)}}{{{\text{c}}{{{\text{n}}}^{2}}\left( {\bar {\tau },\tilde {k}} \right)}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ где ${\text{sn}}\left( {\bar {\tau },\tilde {k}} \right)$ и ${\text{сn}}\left( {\bar {\tau },\tilde {k}} \right)$ – эллиптические синус и косинус Якоби, $\bar {\tau } = \sqrt {{{\tilde {\chi }} \mathord{\left/ {\vphantom {{\tilde {\chi }} 2}} \right. \kern-0em} 2}} \sqrt {{{a}_{1}} - {{a}_{3}}} {{\Omega }}\left( {t - {z \mathord{\left/ {\vphantom {z {\tilde {\nu }}}} \right. \kern-0em} {\tilde {\nu }}}} \right),$ $\tilde {\nu }$ = = $\frac{c}{{{{{\left[ {{{\varepsilon }_{L}} - {{\tilde {\chi }\left( {{{a}_{1}} + {{a}_{2}} + {{a}_{3}}} \right)} \mathord{\left/ {\vphantom {{\tilde {\chi }\left( {{{a}_{1}} + {{a}_{2}} + {{a}_{3}}} \right)} 2}} \right. \kern-0em} 2}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}$ – скорость нелинейной волны, $\tilde {k} = \sqrt {\frac{{{{a}_{1}} - {{a}_{2}}}}{{{{a}_{1}} - {{a}_{3}}}}} $ – модуль эллиптического интеграла первого рода, ${{a}_{1}} > {{a}_{2}} > {{a}_{3}} > {{E}^{2}}$ (см. ПРИЛОЖЕНИЕ). При ${{a}_{1}} > {{a}_{2}} = {{a}_{3}} > {{E}^{2}}$ амплитуда электрического вектора НППП равна E = = ${{\left[ {{{a}_{1}}{\text{sc}}{{{\text{h}}}^{2}}\left( {\bar {\tau }} \right) + {{a}_{2}}{\text{t}}{{{\text{h}}}^{2}}\left( {\bar {\tau }} \right)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ Фаза электрического вектора НППП определяется выражением $\varphi = {{\varphi }_{0}} + {{\tilde {P}}^{2}}\int {\frac{{d\tau }}{{{{E}^{2}}\left( \tau \right)}}} .$ Амплитуда, фаза и скорость волны НППП зависят от постоянных ${{a}_{1}},{{a}_{2}},{{a}_{3}}.$ Постоянные ${{a}_{1}},{{a}_{2}},{{a}_{3}},$ в свою очередь, зависят от интегралов движения $\tilde {E}$ и $\tilde {P},$ а также от значений параметров возбуждающего электромагнитного поля и сред, входящих в выражение для нелинейной восприимчивости $\tilde {\chi } = \frac{\chi }{{{{\varepsilon }_{L}} - n_{f}^{2}}}.$

Таким образом, при возбуждении импульсным сигналом огибающая волнового пакета НППП приобретает форму кноидальной волны, либо форму уединенной волны в виде суммы светлого и темного солитонов, возникающих в результате самомодуляции потока НППП. Такое поведение потока НППП аналогично самомодуляции оптического потока в нелинейной среде или волноводе [4, 24]. Профиль и период волны НППП зависят от параметров: $\tilde {E} = \frac{1}{2}{{\left( {\frac{{d\vec {E}\left( 0 \right)}}{{d\tau }}} \right)}^{2}} + \frac{1}{2}{{{{\Omega }}}^{2}}\left[ {{{E}^{2}}\left( 0 \right) - \frac{1}{2}\tilde {\chi }{{E}^{4}}\left( 0 \right)} \right]$ – энергии и $\tilde {P} = {{E}^{2}}\left( 0 \right)\frac{{d\varphi \left( 0 \right)}}{{d\tau }}$ – азимутального импульса при t = 0 и z = 0.

ЗАКЛЮЧЕНИЕ

На границе раздела немагнитной диэлектрической среды и немагнитного металла формируется ТМ-мода НППП при возбуждении непрерывным или импульсным мощным электромагнитным сигналом в случае выполнения соответствующих граничных условий. В результате влияния керровской нелинейности сред, обусловленной оптическим термоэффектом, а также насыщения нелинейности, поток НППП самомодулируется. Период и амплитуда модуляции потока НППП определяются интенсивностью возбуждающего электромагнитного поля. Полученные в работе уравнения описывают динамику НППП при возбуждении как непрерывным, так и импульсным мощным электромагнитным сигналом с учетом насыщения нелинейности и потерь. При слабом насыщении нелинейности полученная система нелинейных уравнений имеет аналитические решения в форме векторных кноидальной и уединенной волн.

Импульсный электромагнитный сигнал возбуждает волновой пакет НППП с огибающей в форме кноидальной волны, либо с огибающей в форме уединенной волны в виде суммы светлого и темного солитонов, в зависимости от соотношения параметров возбуждающего электромагнитного поля и параметров сред. Профиль огибающей трансформируется, а период кноидальной волны меняется при изменении мощности источника и/или условий возбуждения НППП.

Сравнение динамики НППП, возбужденных непрерывным и импульсным электромагнитными сигналами различной мощности, на основе анализа аналитических и численных решений полученной системы нелинейных уравнений позволяет сделать вывод о том, что от мощности возбуждающего сигнала зависят форма и параметры плазмонного сигнала на выходе волновода. С увеличением мощности возбуждающего сигнала период кноидальной волны, а также скорость и кноидальной, и уединенной волн НППП уменьшаются, что следует учитывать при проектировании устройств плазмонной техники.

Работа выполнена при поддержке Российского научного фонда (проект № 19-72-20154).