Известия РАН. Серия физическая, 2022, T. 86, № 2, стр. 282-286

ВВЕДЕНИЕ

На данный момент широкое внимание исследователей привлекает обобщенная синхронизация – хаотическое явление радиофизики [1, 2], характеризующееся связью между состояниями взаимодействующих систем (генераторов) в форме функционального соотношения (в общем виде – функционала) [2, 3]. Данное нелинейное явление может возникать не только при однонаправленной, но и при взаимной связи и имеет широкую область применения, например, в медицине [4], при скрытой передаче информации [5] и т.д. При небольшом отклонении параметра связи от критического значения вместо полного отсутствия обобщенной синхронизации наблюдается перемежающееся поведение, характеризующееся чередованием временных интервалов синхронной и асинхронной динамики [6].

В ходе проведения исследований обнаружена мультистабильность в поведении однонаправленно связанных хаотических систем вблизи границы обобщенной синхронизации. Данное явление наблюдается при взаимодействии большого количества связанных систем, стартующих с различных начальных условий, когда при определенных значениях параметра связи в один и тот же момент времени часть систем демонстрирует синхронную динамику, в то время как другая часть систем находится в асинхронном режиме.

Вопрос о существовании мультистабильности в случае взаимной связи до сих пор остается открытым. При исследовании связанных хаотических систем при помощи метода локальных ляпуновских показателей [7] было обнаружено явление перемежаемости на границе обобщенной синхронизации не только в случае однонаправленной, но и в случае взаимной связи, что позволяет предположить возможность существования мультистабильности также и в последнем случае. В связи с этим, в данной работе исследуется возможность существования мультистабильности в случае как однонаправленной, так и взаимной связи.

ИССЛЕДОВАНИЕ ВОЗМОЖНОСТИ СУЩЕСТВОВАНИЯ МУЛЬТИСТАБИЛЬНОСТИ ПРИ ПОМОЩИ ЛОКАЛЬНЫХ ЛЯПУНОВСКИХ ПОКАЗАТЕЛЕЙ

В качестве примеров были рассмотрены N пар систем однонаправленно и взаимно связанных хаотических осцилляторов Ресслера, описываемых следующей системой дифференциальных уравнений [2, 5, 8]:

где i = 1, 2, …, N – индекс пары систем, a = 0.15, b = 0.2, c = 10.0, ${{\omega }_{1}} = 0.93,$ ${{\omega }_{2}} = 0.95$ – управляющие параметры, $\dot {x},\dot {y},\dot {z}$ – производные по безразмерному времени. Нижние индексы соответствуют номеру системы относительно отдельно взятой пары. Параметры связи ${{{{\varepsilon }}}_{1}} = 0,$ ${{{{\varepsilon }}}_{2}} = {{\varepsilon }}$ в случае однонаправленной связи, и ${{{{\varepsilon }}}_{1}} = {{{{\varepsilon }}}_{2}} = {{\varepsilon }}$ – в случае взаимной. Управляющие параметры были заданы таким образом, чтобы после переходного процесса при любых начальных условиях всегда наблюдался режим перемежающейся обобщенной синхронизации.

Данная система решалась численно при помощи метода Рунге–Кутта 4 порядка с шагом интегрирования 0.001. Начальные условия систем под индексом 1 (в случае однонаправленной связи – ведущих систем) оставались неизменными. Во всех остальных случаях начальные условия были заданы таким образом, чтобы добиться максимального покрытия аттракторов. Во избежание “ловушки численного счета” в управляющий параметр ${{{{\omega }}}_{2}}$ добавлялась слабая расстройка (порядка 10^–8) с равномерной плотностью распределения вероятности.

Существуют различные методы, доступные для анализа мультистабильности. Наиболее часто применяется метод вспомогательной системы [9] в связи с его простотой реализации и высокой точностью в случае однонаправленной связи. К сожалению, данный подход оказывается неприменим в случае взаимной связи [10]. В связи с этим, в данной работе для анализа использовался метод расчета локальных ляпуновских показателей [11, 12]. Ранее этот подход уже использовался нами для исследования характеристик перемежающейся обобщенной синхронизации в двух однонаправленно и взаимно связанных системах [7].

В качестве меры мультистабильности рассматривалась вероятность детектирования асинхронного (в смысле режима обобщенной синхронизации) участка временной динамики по формуле:

где M $ \gg $ 1 – число осцилляторов, участвующих в рассмотрении, ${{\Lambda }}_{2}^{i}$ – второй по старшинству ляпуновский показатель, $n\left( {{{\Lambda }}_{2}^{i}} \right)$ – количество систем, находящихся в синхронизме с i-м осциллятором. В данном случае, под синхронизмом подразумевается выполнение условия ${{\Lambda }}_{2}^{i} < {{\Delta ,}}$ где Δ = 0.005 – наперед заданная положительная константа [6]. Стоит отметить, что данная величина может быть задана произвольно, однако она должна быть достаточно малой, чтобы выполнялось условие синхронизма, но не слишком малой, чтобы исключить влияние флуктуаций второго локального показателя Ляпунова.

Стоит отметить, что желательно рассматривать достаточно большое количество пар (порядка 1000), т. к. в таком случае исключается ошибка, если системы рассматриваются при различных начальных условиях, равномерно покрывающих аттракторы систем. Однако, после покрытия аттрактора начальными условиями приблизительно на 99.99% дальнейшее увеличение числа систем не приведет к значительному улучшению точности.

Сначала была определена зависимость спектра ляпуновских показателей от параметра связи (см. рис. 1). Как видно из рис. 1, при определенном критическом значении параметра связи второй по старшинству ляпуновский показатель обращается в ноль. Данный момент и соответствует установлению режима обобщенной синхронизации. Стоит также отметить, что в случае взаимной связи наблюдается множество окон периодичности (например, при ${{\varepsilon }} \in \left[ {0.03;0.036} \right],$ ${{\varepsilon }} \in \left[ {0.044;0.048} \right]$ и т.д.), характеризующихся нулевым значением старшего показателя Ляпунова.

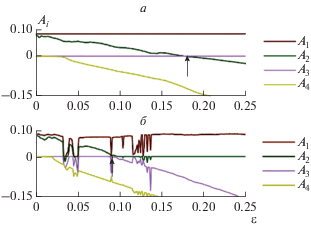
Важно отметить, что оценка порога возникновения обобщенной синхронизации при помощи спектра ляпуновских показателей оказывается немного заниженной. На практике, перемежающаяся динамика наблюдается при значениях параметра связи немного больше критического (${{\varepsilon }} < 0.19$ в случае однонаправленной связи и ${{\varepsilon }} < 0.11$ в случае взаимной связи). Причиной этого является то, что спектр отражает динамику, усредненную по времени, и не учитывает кратковременные асинхронные колебания.

Далее, для иллюстрации явления мультистабильности при помощи метода локальных ляпуновских показателей были получены бассейны притяжения аттрактора второй системы (1) (см. рис. 2) в случае однонаправленной (при ε = 0.17) и взаимной (при ε = 0.095) связи.

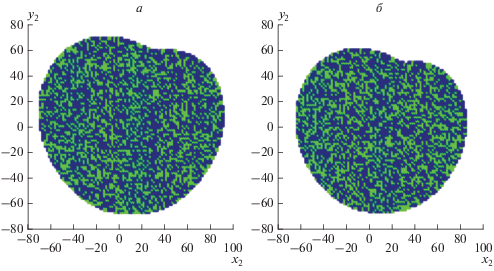
Для расчета бассейнов притяжения моделировалась одна пара систем при фиксированных значениях параметра связи при определенном значении безразмерного времени t, при фиксированных начальных условиях первой системы и начальной координаты ${{z}_{2}}$ второй системы. Из рис. 2 видно, что вблизи границы синхронного режима действительно наблюдается мультистабильность не только при однонаправленной связи, но и при взаимной.

В ходе работы была получена численная оценка зависимости вероятности наблюдения асинхронного поведения от параметра связи, усредненная по 1000 рассматриваемых пар связанных систем (см. рис. 3).

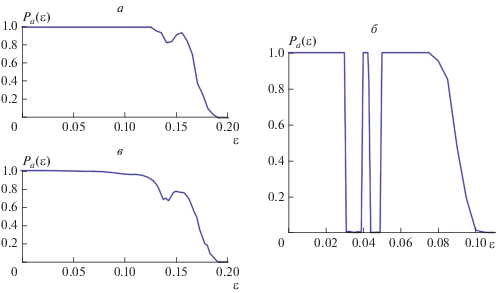
Рисунок 3 подтверждает существование мультистабильности при однонаправленной, и взаимной связи. Все системы находятся в синхронизме при ${{\varepsilon }_{c}} = 0.19$ и ${{\varepsilon }_{c}} = 0.11$ соответственно для случая однонаправленной и случая взаимной связи. Также стоит отметить, что на втором графике имеются области периодичности в тех же диапазонах, что и на зависимости спектра ляпуновских показателей от параметра связи.

Для подтверждения корректности полученных результатов была определена аналогичная характеристика в случае однонаправленной связи при помощи модификации метода вспомогательной системы [9] (см. рис. 3в). Данный метод заключается в том, что к каждой паре связанных систем вводится дополнительная (вспомогательная) система, описываемая уравнениями ведомой системы, но имеющая иные начальные условия, лежащие в том же бассейне притяжения. Тогда, синхронизм будет проявляться при эквивалентности состояний ведомой и вспомогательной систем.

В данном случае вероятность детектирования асинхронных участков временной динамики определялась по формуле, аналогичной формуле (2):

где ${{d}^{i}} = \sqrt {\left( {x_{2}^{i} - x_{{2a}}^{i}} \right) + \left( {y_{2}^{i} - y_{{2a}}^{i}} \right) + \left( {z_{2}^{i} - z_{{2a}}^{i}} \right)} $ (индекс 2a соответствует вспомогательной системе). Условием выполнения синхронизма является ${{d}^{i}} < \Delta ,$ $\Delta = 0.01.$

При сопоставлении результатов, полученных обоими методами, наблюдаются небольшие расхождения. Причиной их появления могло послужить то, что распределение N(${{P}_{a}}$) по вероятности наблюдения асинхронной временной динамики различается в зависимости от используемого метода (см. рис. 4). Распределение рассчитывалось для временной зависимости P_a(t) в течение всего времени наблюдения.

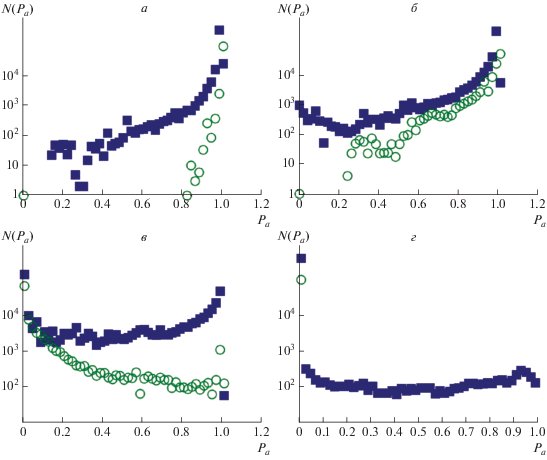
При использовании обоих методов указанные распределения при малых значениях параметра связи представляют собой практически степенную функцию, а при увеличении параметра связи распределение сглаживается в области ${{P}_{a}} > 0$ с одновременным увеличением N(0). Отклонение между результатами обоих методов можно объяснить рядом факторов, например, недостаточно оптимальным набором параметров метода локальных ляпуновских показателей (времени накопления и порога возникновения синхронизации).

Тем не менее, зависимости меры мультистабильности от параметра связи, полученные обоими методами, отличаются лишь количественно, но не качественно. В частности, при ${{\varepsilon }} \approx 0.14$ наблюдается небольшое углубление, которое также присутствует и на спектре показателей Ляпунова (см. второй старший показатель). После установления обобщенной синхронизации ($\varepsilon > 0.2$) распределения для обоих методов представляют собой только значение N(0), что говорит об отсутствии асинхронных участков временной динамики.

ЗАКЛЮЧЕНИЕ

При помощи метода локальных ляпуновских показателей было установлено, что явление мультистабильности может возникать не только в случае однонаправленной, но и в случае взаимной связи. Наблюдается хорошее соответствие полученных результатов с результатами других работ и теоретическими зависимостями [6, 10]. Корректность результатов метода локальных показателей Ляпунова также подтверждена путем сравнения с результатами, полученными методом вспомогательной системы.

Таким образом, данный метод можно использовать для анализа мультистабильности при перемежающейся обобщенной синхронизации. Несмотря на то, что в данной работе были рассмотрены только потоковые системы, аналогичные результаты можно получить и в случае дискретных хаотических систем.

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 19-12-00037).