1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 2, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 2, стр. 293-297

О влиянии характеристик шумового сигнала на установление обобщенной синхронизации в системах со сложной топологией аттрактора

В. А. Ханадеев 1, 2, *, О. И. Москаленко 1, 2

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Саратовский национальный исследовательский государственный университет имени Н.Г. Чернышевского”
Саратов, Россия

2 Региональный научно-образовательный математический центр “Математика технологий будущего”
Саратов, Россия

* E-mail: v.a.hanadeev@gmail.com

Поступила в редакцию 01.10.2021
После доработки 11.10.2021
Принята к публикации 22.10.2021

Полный текст (PDF)

Аннотация

Выполнен анализ влияния характеристик шумового сигнала на границу возникновения режима обобщенной синхронизации в системах со сложной топологией аттрактора. Установлено, что вне зависимости от типа шума режим обобщенной синхронизации оказывается устойчивым к шумам в широком, но ограниченном диапазоне изменения интенсивности шума.

ВВЕДЕНИЕ

Одним из направлений нелинейной динамики, вызывающих большой интерес современных ученых, является изучение синхронизации неавтономных и связанных динамических систем, способных демонстрировать хаотическую динамику [1, 2]. Такое внимание исследователей к явлению хаотической синхронизации обусловлено, в первую очередь, его фундаментальностью. В то же самое время, известно, что это явление может найти практическое применение, например, в задачах передачи информации [3, 4], в том числе, скрытой, при диагностике динамики некоторых биологических систем [5–7], при контроле хаоса в СВЧ генераторах [8] и пр.

За последние несколько десятилетий обнаружено много разных типов хаотической синхронизации, среди которых не угасает интерес к исследованию режима обобщенной синхронизации [9]. Этот режим может наблюдаться как в однонаправленно, так и взаимно связанных хаотических системах, и подразумевает установление функционала между их состояниями. В случае однонаправленной связи этот функционал имеет вид y = = F[x], а для диагностики этого режима традиционно рассчитывается старший условный показатель Ляпунова [10] или используется метод вспомогательной системы [11].

Важным вопросом при изучении обобщенной синхронизации является анализ влияния шума на установление этого синхронного режима [12, 13]. На данный момент хорошо известно, что в системах с аттрактором ленточного типа (как, например, у систем Ресслера) с диссипативным типом связи [14–16] этот режим является устойчивым к шумам [13, 17], что позволяет предложить способы скрытой передачи информации, эффективно работающие, в том числе, при наличии высокого уровня шума в канале связи [18]. Изучение этого режима в более сложных системах находится только в начале своего развития и, несмотря на наличие работ по этой тематике (см., например, [19]), требует дополнительного внимания и изучения.

Выполнен анализ влияния характеристик внешнего шумового воздействия на установление режима обобщенной синхронизации в системах с так называемой сложной топологией аттрактора. При этом, под системами со сложной (двулистной) структурой аттрактора понимаются такие системы, фазовое пространство которых состоит из двух подпространств с небольшой общей областью, внутри которой фазовые траектории могут переходить из одного подпространства в другое и наоборот [20]. В качестве примеров таких систем рассмотрены однонаправленно диссипативно связанные системы Лоренца и системы Чена, а в качестве источников шумового воздействия – белый шум с гауссовой плотностью распределения вероятностей и цветной шум с равномерной плотностью распределения вероятностей. Можно предположить, что ввиду диссипативного типа связи режим обобщенной синхронизации в изучаемых системах будет устойчив по отношению к шумам.

ОБЪЕКТ И МЕТОДЫ ИССЛЕДОВАНИЯ

Однонаправленно связанные системы Лоренца [20] описываются следующей системой обыкновенных дифференциальных уравнений:

(1)
$\begin{array}{*{20}{l}} {{{{\dot {x}}}_{1}} = {{\sigma }}\left( {{{y}_{1}} - {{x}_{1}}} \right),} \\ {{{{\dot {y}}}_{1}} = {{r}_{1}}{{x}_{1}} - {{y}_{1}} - {{x}_{1}}{{z}_{1}},} \\ {\begin{array}{*{20}{l}} {{{{\dot {z}}}_{1}} = - b{{z}_{1}} + {{x}_{1}}{{y}_{1}},} \\ {{{{\dot {x}}}_{2}} = {{\sigma }}\left( {{{y}_{2}} - {{x}_{2}}} \right) + {{\varepsilon }}\left( {{{x}_{1}} - {{x}_{2}}} \right) + D\zeta ,} \\ {\begin{array}{*{20}{l}} {{{{\dot {y}}}_{2}} = {{r}_{2}}{{x}_{2}} - {{y}_{2}} - {{x}_{2}}{{z}_{2}},} \\ {{{{\dot {z}}}_{2}} = - b{{z}_{2}} + {{x}_{2}}{{y}_{2}},} \end{array}} \end{array}} \end{array}$
где $\vec {x}$1,2 = (x1,2, y1,2, z1,2) – векторы состояний взаимодействующих ведущей и ведомой систем, соответственно, ${{\sigma }}$ = 10, b = 2, r1 = 40 и r2 = 35 – управляющие параметры, ε – параметр связи, D – интенсивность шумового воздействия, $\zeta ~$ – дельта-коррелированный белый гауссов шум с нулевым средним или цветной шум с нулевым средним и равномерной плотностью распределения вероятностей.

Уравнения однонаправленно связанных систем Чена [21] являются модификацией уравнений систем Лоренца и записываются в следующем виде:

(2)
$\begin{array}{*{20}{l}} {{{{\dot {x}}}_{1}} = {{\sigma }}\left( {{{y}_{1}} - {{x}_{1}}} \right) + e{{y}_{1}}{{z}_{1}},} \\ {{{{\dot {y}}}_{1}} = c{{x}_{1}} - d{{x}_{1}}{{z}_{1}} + {{y}_{1}} + {{u}_{1}},} \\ {\begin{array}{*{20}{l}} {{{{\dot {z}}}_{1}} = {{x}_{1}}{{y}_{1}} - b{{z}_{1}},} \\ {{{{\dot {u}}}_{1}} = - {{k}_{1}}{{y}_{1}},} \\ {\begin{array}{*{20}{l}} {{{{\dot {x}}}_{2}} = a({{y}_{2}} - {{x}_{2}}) - e{{y}_{2}}{{z}_{2}},} \\ \begin{gathered} {{{\dot {y}}}_{2}} = c{{x}_{2}} + d{{x}_{2}}{{z}_{2}} + {{y}_{2}} + {{u}_{2}}, \hfill \\ {{{\dot {z}}}_{2}} = {{x}_{2}}{{y}_{2}} - b{{z}_{2}}, \hfill \\ {{{\dot {u}}}_{2}} = - {{k}_{2}}{{y}_{2}} + \varepsilon ({{x}_{1}} - {{x}_{2}}) + D\zeta . \hfill \\ \end{gathered} \end{array}} \end{array}} \end{array}$
где a = 35, b = 4.9, c = 25, d = 5, e = 35, k1 = 190, k2 = = 110 – управляющие параметры, ε – параметр связи, слагаемое D соответствует источнику шума с теми же характеристиками, что и для системы (1). Управляющие параметры k1 и k2 подобраны таким образом, что первая система находится в хаотическом режиме, а вторая система в режиме гиперхаоса.

Решение систем (1) и (2) осуществлялось путем численного решения стохастических дифференциальных уравнений методом Рунге–Кутта 4 порядка, адаптированным на данный случай [22], с шагом h = 0.001. Режим обобщенной синхронизации в системах (1) и (2), как отмечалось во Введении, диагностировался при помощи метода вспомогательной системы [11] и путем расчета спектра показателей Ляпунова [10].

Метод вспомогательной системы заключается в рассмотрении дополнительной системы, так называемой вспомогательной системы u, идентичной ведомой системе y по управляющим параметрам, начальные условия которой u(0) отличаются от начальных состояний ведомой системы y(0), но находятся в бассейне притяжения того же самого аттрактора [11]. При этом, и ведомая, и вспомогательная системы должны подвергаться одному и тому же воздействию как со стороны ведущей системы, так и шумового сигнала. В отсутствие режима обобщенной синхронизации между исходными однонаправленно связанными системами состояния ведомой y и вспомогательной u систем являются различными, однако, эти системы эволюционируют на одном и том же хаотическом аттракторе. Если исходные ведущая и ведомая системы находятся в режиме обобщенной синхронизации, состояния ведомой и вспомогательной систем после завершения переходного процесса будут тождественно равны y ≡ u в силу выполнения соотношений y = F[x] и, соответственно, u = F[x] [11].

Для анализа режима обобщенной синхронизации при помощи вычисления спектра показателей Ляпунова необходимо рассчитать так называемый старший условный показатель Ляпунова – старший ляпуновский показатель ведомой системы – при изменении параметра связи. Когда этот показатель Ляпунова становится отрицательным, в исходных однонаправленно связанных системах диагностируется наступление режима обобщенной синхронизации [10].

Известно, что метод расчета спектра показателей Ляпунова дает несколько заниженную оценку критического значения установления синхронного режима по сравнению с методом вспомогательной системы, что обусловлено наличием перемежающегося поведения вблизи границы обобщенной синхронизации [10, 15, 19]. Метод вспомогательной системы, в свою очередь, может привести к неточному определению порога обобщенной синхронизации из-за возникновения “ловушки” численного счета, во избежание которой необходимо ввести в рассмотрение небольшую расстройку между параметрами ведомой и вспомогательной систем. С целью оптимального выбора величины расстройки и более точного детектирования режима обобщенной синхронизации в данной работе оба метода использовались одновременно.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ

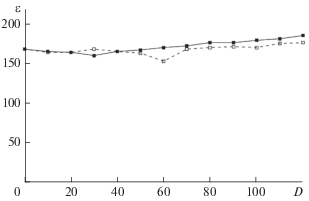
Применим метод вспомогательной системы и расчет старшего условного показателя Ляпунова для определения границ обобщенной синхронизации при изменении интенсивности шумового воздействия в системах (1) и (2). На рис. 1 приведены рассчитанные таким образом границы обобщенной синхронизации в системе двух однонаправленно связанных осцилляторов Лоренца (1) для двух типов шумового воздействия, упомянутых в предыдущем разделе. На рисунке наглядно видно, что полученные границы оказываются близки друг к другу. Более того, пороговые значения установления синхронных режимов оказывается практически одинаковыми в широком диапазоне изменения интенсивности шумового воздействия как для белого, так и цветного шума. Иными словами, режим обобщенной синхронизации в системе (1) оказывается устойчивым к шумам независимо от интенсивности и типа шумового воздействия.

Рис. 1.

Зависимости порога возникновения режима обобщенной синхронизации в двух однонаправленно связанных системах Лоренца (1) от интенсивности шумового воздействия с гауссовой плотностью распределения вероятностей (сплошная линия) и равномерной плотностью распределения вероятностей (пунктирная линия).

На рис. 2 показаны зависимости старшего условного показателя Ляпунова от параметра связи для систем Лоренца в отсутствии шума и при наличии шума одинаковой интенсивности D = 8 с гауссовым и равномерным распределениями вероятностей. Видно, что приведенные зависимости немного отличаются друг от друга. Однако, во всех рассмотренных случаях с ростом величины параметра связи старший условный показатель Ляпунова переходит в отрицательную область практически при одинаковых значениях параметра связи, что и соответствует практически одним и тем же порогам установления обобщенной синхронизации в исследуемой системе. На рис. 3 представлены фазовые портреты ведомой системы Лоренца при тех же значениях характера и интенсивности шумового воздействия. Из рисунка видно, что при добавлении шума аттрактор Лоренца заметно трансформируется, в частности, для обоих источников шума происходит его достаточно сильное зашумление, но в обоих случаях двулистная структура аттрактора сохраняется, что может быть причиной устойчивости режима обобщенной синхронизации к шумам.

Рис. 2.

Зависимости старшего условного показателя Ляпунова ${{\lambda }}_{1}^{r}$ системы (1) от параметра связи ε в отсутствии и при наличии различных типов шумового воздействия. Сплошной линией показан старший ляпуновский показатель в отсутствии шума D = 0, штриховой линией – при воздействии шума с гауссовым распределением интенсивности D = 8, и штрих-пунктирной линией – при воздействии шума с равномерным распределением интенсивности D = 8.

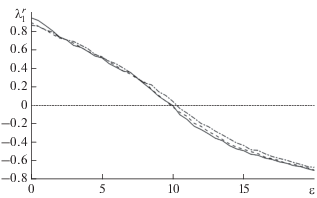
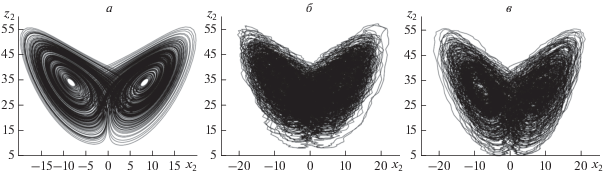
Рис. 3.

Фазовые портреты ведомой системы Лоренца (1) в отсутствие шума (a) и при наличии шума интенсивности D = 8 с гауссовым (b) и равномерным распределениями (c).

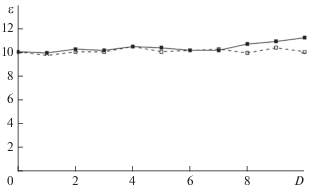
Аналогичное поведение границ обобщенной синхронизации наблюдается и для однонаправленно связанных систем Чена. На рис. 4 приведены зависимости порога возникновения режима обобщенной хаотической синхронизации от интенсивности шума для систем Чена, находящихся под воздействием шума с гауссовым и равномерным распределениями. Легко видеть, что по аналогии с осцилляторами Лоренца, при различных типах шумового воздействия границы режима обобщенной синхронизации практически не зависят от интенсивности шума D ∈ [0; 120]. Устойчивость режима обобщенной синхронизации в двух однонаправленно связанных системах Чена по отношению к шумам обусловлена также слабым влиянием шума на структуру аттрактора ведомой системы и поведение старшего условного показателя Ляпунова.

Рис. 4.

Зависимости порога возникновения режима обобщенной синхронизации в двух однонаправленно связанных системах Чена (2) от интенсивности шума с гауссовой плотностью распределения вероятностей (сплошная линия) и равномерной плотностью распределения вероятностей (пунктирная линия).

ЗАКЛЮЧЕНИЕ

Таким образом, проведено исследование влияния двух типов шумового воздействия на установление режима обобщенной синхронизации в системах со сложной (двулистной) топологией аттрактора с однонаправленным типом связи. С помощью метода вспомогательной системы и расчета старшего условного показателя Ляпунова установлено, что характер шумового сигнала не оказывает существенного влияния на порог возникновения синхронного режима как в системах Лоренца, так и осцилляторах Чена. Независимо от типа шумового воздействия режим обобщенной синхронизации в системах со сложной топологией аттрактора оказывается устойчивым по отношению к шумам в широком, но ограниченном диапазоне изменения интенсивности шумового воздействия.

Подобное поведение однонаправленно связанных систем, находящихся под действием шума, обусловлено слабым влиянием шумового сигнала на двулистную структуру аттрактора ведомой системы и величину старшего условного показателя Ляпунова, отвечающего за установление обобщенной синхронизации в таких системах.

Работа выполнена при финансовой поддержке Совета по грантам Президента Российской Федерации для государственной поддержки молодых российских ученых – докторов наук (проект № МД-21.2020.2).

Список литературы

  1. Pikovsky A., Rosenblum M., Kurths J. Synchronization: a universal concept in nonlinear sciences. N.Y.: Cambridge Univ. Press, 2001. 411 p.

  2. Анищенко В.С. Сложные колебания в простых системах. Механизмы возникновения, структура и свойства динамического хаоса в радиофизических системах. М.: URSS, 2009. 320 с.

  3. Kocarev L., Parlitz U. // Phys. Rev. Lett. 1995. V. 74. No. 25. P. 5028.

  4. Короновский А.А., Москаленко О.И., Храмов А.Е. // УФН. 2009. Т. 179. № 12. С. 1281.

  5. Pavlov A., Sosnovtseva O., Ziganshin A. et al. // Phys. A. 2002. V. 316. No. 1–4. P. 233.

  6. Масленников О.В., Некоркин В.И. // УФН. 2017. Т. 187. С. 745.

  7. Храмов А.Е., Фролов Н.С., Максименко В.А. и др. // УФН. 2021. Т. 191. С. 614.

  8. Dmitriev B.S., Hramov A.E., Koronovskii A.A. et al. // Phys. Rev. Lett. 2009. V. 102. No. 7. Art. No. 074101.

  9. Rulkov N.F., Sushchik M.M., Tsimring L.S., Abarbanel H.D.I. // Phys. Rev. E. 1995. V. 51. No. 2. P. 980.

  10. Pyragas K. // Phys. Rev. E. 1996. V. 54. No. 5. Art. No. R4508.

  11. Abarbanel H.D.I., Rulkov N.F., Sushchik M.M. // Phys. Rev. E. 1996. V. 53. No. 5. P. 4528.

  12. Toral R., Mirasso C.R., Hernández-García E., Piro O. // Chaos. 2001. V. 11. P. 665.

  13. Moskalenko O.I., Hramov A.E., Koronovskii A.A., Ovchinnikov A.A. // Eur. Phys. J. B. 2011. V. 82. No. 1. P. 69.

  14. Hramov A.E., Koronovskii A.A. // Phys. Rev. E. 2005. V. 71. Art. No. 067201.

  15. Hramov A.E., Koronovskii A.A., Moskalenko O.I. // Europhys. Lett. 2005. V. 72. No. 6. P. 901.

  16. Hramov A.E., Koronovskii A.A., Moskalenko O.I. // Phys. Lett. A. 2006. V. 354. No. 5–6. P. 423.

  17. Короновский А.А., Москаленко О.И., Овчинников А.А., Храмов А.Е. // Изв. РАН. Сер. физ. 2009. Т. 73. № 12. С. 1726; Koronovskii A.A., Moskalenko O.I., Ovchinnikov A.A., Hramov A.E. // Bull. Russ. Acad. Sci. Phys. 2009. V. 73. No. 12. P. 1616.

  18. Moskalenko O.I., Koronovskii A.A., Hramov A.E. // Phys. Lett. A. 2010. V. 374. No. 29. P. 2925.

  19. Москаленко О.И., Ханадеев В.А. // Изв. Саратов. ун-та. Сер. физ. 2021. Т. 21. No. 3. С. 233.

  20. Ханадеев В.А., Москаленко О.И., Короновский А.А. // Изв. РАН. Сер. физ. 2021. Т. 85. № 2. С. 265; Khanadeev V.A., Moskalenko O.I., Koronovskii A.A. // Bull. Russ. Acad. Sci. Phys. 2021. V. 85. No. 2. P. 192.

  21. Chen Z., Yang Y., Qi G., Yuan Z. // Phys. Lett. A. 2007. V. 360. No. 6. P. 696.

  22. Никитин Н.Н., Первачев С.В., Разевиг В.Д. // Автомат. и телемех. 1975. № 4. С. 133.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал