Известия РАН. Серия физическая, 2022, T. 86, № 2, стр. 298-304

ВВЕДЕНИЕ

Важным, и малоизученным, является вопрос о возможных режимах систем с самоорганизованной критичностью (ССК) вблизи точки бифуркации [1–4]. Данная работа посвящена не описанию режимов после прохождения критической точки и последующим событиям, а изучению возможных стабильных устойчивых режимов при работе в непосредственной близости от критической точки. Устойчивость неустойчивых режимов достигается за счет нелинейной отрицательной обратной связи. Показано, что в рассматриваемой неустойчивой области возможно существование режимов с замечательными свойствами, которые широко используются во всем живом, физике, технических устройствах, изобретенных человеком. Это следующие свойства: 1) значительное (до миллионов раз) усиление входных сигналов; 2) значительное повышение избирательности к внешним воздействиям; 3) значительное увеличение возможностей развития и размножения.

Иллюстрация этих замечательных возможностей реализована на примере формирования импульсных потоков, идущих в ЦНС, под действием малого рецепторного потенциала в физиологических сенсорных системах [5–7]. Приведена реализация ССК в технических системах на примере радиоприемных устройств реализации сверхбольших усилений и избирательность при приеме сверхслабых радиосигналов [8].

КРИТИЧЕСКИЕ ТОЧКИ – ТОЧКИ БИФУРКАЦИИ СИСТЕМ С САМООРГАНИЗОВАННОЙ КРИТИЧНОСТЬЮ

Самоорганизованная критичность — свойство динамических систем, которые имеют точки бифуркации. Поведение в окрестности точки характеризуется тем, что при малом возмущении система может пройти точку бифуркации, тем самым полностью изменив свою модель поведения. Классическими примерами самоорганизованной критичности является фазовый переход или модель песчаной кучи.

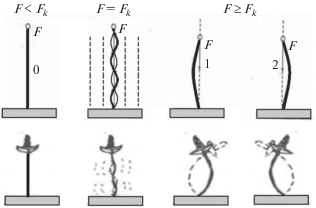
Для систем с самоорганизованной критичностью характерно наличие критических состояний, при которых система становится неустойчивой относительно флуктуаций и возникает неопределенность: станет ли состояние системы хаотическим или она перейдет на новый, более дифференцированный и высокий уровень упорядоченности. Под критическими точками систем с самоорганизованной критичностью обычно понимают так называемые точки бифуркации, при прохождении которых возможно появление двух устойчивых состояния, что иллюстрируется рис. 1.

В критической точке система становится неустойчивой и может перейти в одно из двух устойчивых состояний. В общем случае из критической точки система может переходить в n устойчивых состояний.

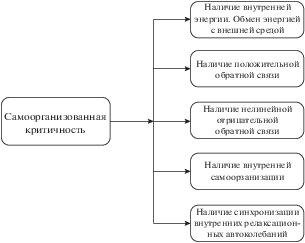
ССК представляет сложную систему, для которой характерно включение подсистем, обладающих свойствами: наличие внутренней энергии, наличие положительной обратной связи, наличие нелинейной отрицательной обратной связи, наличие внутренней организации, наличие синхронизации внутренних релаксационных автоколебаний и другие. Структура ССК показана на рис. 2.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЛЯ ИССЛЕДОВАНИЯ РЕЖИМОВ В СИСТЕМАХ С САМООРГАНИЗОВАННОЙ КРИТИЧНОСТЬЮ ВБЛИЗИ НЕУСТОЙЧИВОЙ ТОЧКИ – ТОЧКИ БИФУРКАЦИИ

Определим коротко свойство систем с самоорганизованной критичностью (ССК). Теория ССК – новейшее направление в разработке теории нелинейных динамических систем. Ее суть в том, что по мере развития нелинейной системы она неизбежно приближается к точке бифуркации, ее устойчивость падает, и в ней создаются условия, при которых малый толчок может спровоцировать лавину с непредсказуемыми последствиями, изменяющими всю систему. В нелинейной динамике систем примером ССК может служить автогенератор с положительной обратной связью, показанный на рис. 3.

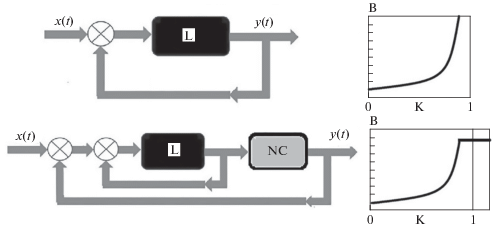
Структурная схема автогенераторов с положительной обратной связью и отрицательной нелинейной обратной связью показана на рис. 3 снизу. Справа показана амплитудная характеристика, которая стабилизирована отрицательной нелинейной обратной связью. NC – блок, характеризующий, например, нейронный узел.

Вблизи порога самовозбуждения автогенератор является ССК. Достаточно самого малого входного сигнала, чтобы вызвать ответ автогенератора со значительной амплитудой. С физической точки зрения автогенератор самовозбуждается. Уравнение автогенератора в случае, когда он содержит линейное звено, имеющее коэффициент передачи равный k, имеет вид $y = \frac{{kx}}{{1 - k}},$ где $y$ – выходной сигнал. Критический уровень усиления $k$ = 1, при этом сигнал $y$ при отсутствии нелинейности стремится к $\infty .$ Такое поведение ССК иллюстрируется рис. 3 справа. При плавном приближении $k$ к 1 система становится неустойчивой и не может быть реализована на практике. Для использования полезных свойств систем с самоорганизованной критичностью на пороге самовозбуждения или в режиме бифуркации может быть использована отрицательная нелинейная обратная связь. Она позволяет значительно увеличить чувствительность преобразования, и в то же время будет препятствовать возникновению неустойчивости. Это позволяет значительно увеличить качество работы системы. Система с саморганизованной критичностью в виде автогенератора с положительной обратной связью, дополненного отрицательной нелинейной обратной связью, показана на рис. 3 снизу.

Режимы работы ССК вблизи точки бифуркации в ряде случаев можно рассматривать по существу как пороговую синхронизацию релаксационных потенциально автоколебательных или автоколебательных систем. В настоящее время для исследования синхронизации релаксационных автоколебательных систем известно два метода: метод обыкновенных дифференциальных уравнений с малыми параметрами перед производными [9] и метод, использующий модифицированный аксиоматический метод Винера–Розенблюта в сочетании со свойствами равномерных почти-периодических функций [10–14].

Согласно первому методу для исследования синхронизации релаксационных автоколебаний используются системы дифференциальных уравнений с малым параметром при производных

где $x = ({{x}_{1}},...,{{x}_{k}}),$ $y = ({{y}_{1}},...,{{y}_{l}}),$ $f = ({{f}_{1}},...,{{f}_{k}}),$ $g = ({{g}_{1}},...,{{g}_{l}}),$ ${{\beta }_{1}}({\text{t}}),{{\beta }_{2}}({\text{t}})$ – синхронизирующие воздействия. Точные аналитические решения приведенных уравнений неизвестны, не существуют также и приближенные методы решения уравнений [9].

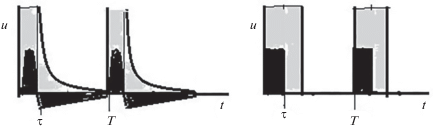
Рассмотрим второй метод исследования синхронизации релаксационных автоколебаний. В работах [10–14] предложен метод получения точных аналитических решений задачи синхронизации, уравнения системы задаются в модифицированной аксиоматической форме. Простейшая форма релаксационной системы предложена Н. Винером и А. Розенблютом в 1946 г. [15]. Геометрическая интерпретация формы релаксационных колебаний в предлагаемой модели и модели Винера–Розенблюта показаны на рис. 4 слева и справа.

Модифицированная аксиоматическая модель релаксационной системы задается, в сочетании со свойствами равномерных почти-периодических функций предложена в работах [10–14]. Она имеет вид

где: $f(t)$ – функция, характеризующая форму релаксационного автоколебания; ${{f}_{1}}(t),$ ${{f}_{2}}(t)$ – функции в интервале “быстрого” и “медленного” изменения релаксационного автоколебания; ${{f}_{{\text{д}}}}(t)$ – динамический порог возбуждения; ${{f}_{3}}(t)$ – функция, характеризующая динамический порог возбуждения для “медленной” фазы; R – функция остаток от деления t на ${{T}_{c}}$ $R = t - \bmod (t,{{T}_{c}});$ $\bmod (t,{{T}_{c}})$ – функция частное от деления t на ${{T}_{c}};$ (3) – неравенство Кронекера [16], ${{T}_{c}},T$ – периоды синхронизирующего сигнала и релаксационного осциллятора; $\varepsilon = f_{{\text{д}}}^{{ - 1}}({{U}_{c}}){\text{;}}$ $f_{{\text{д}}}^{{ - 1}}$ – функция обратная функции ${{f}_{{\text{д}}}}{\text{;}}$ ${{U}_{c}}$ – амплитуда переднего фронта импульса возбуждения.

ИССЛЕДОВАНИЕ РЕЖИМОВ ВБЛИЗИ ТОЧКИ БИФУРКАЦИИ СИСТЕМ С САМООРГАНИЗОВАННОЙ КРИТИЧНОСТЬЮ ПРИ ГЕНЕРАЦИИ ИМПУЛЬСНЫХ ПОТОКОВ В ФИЗИОЛОГИЧЕСКИХ СЕНСОРНЫХ СИСТЕМАХ

Генераторный потенциал в сенсорных нейронах возбуждается от непрерывно меняющегося потенциала, приходящего от рецептора. Местом преобразования рецепторного потенциала в одиночные импульсы или импульсные потоки в виде спайков или периодических импульсных потоков являются специальные места нейронов, называемые аксонным холмиком. Место возникновения импульсных ответов в нейроне брюшка речного рака и зрительного анализатора человека иллюстрируется рис. 5 [5–8].

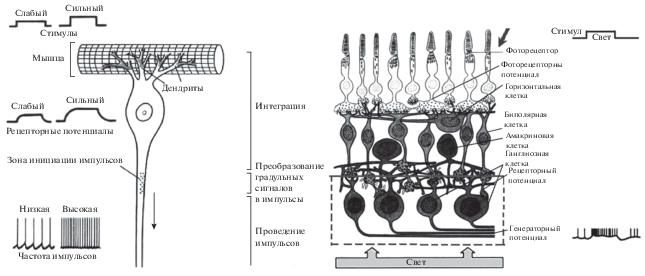
Рецептор находится в специализированном мышечном пучке, лежащем на дорсальной поверхности мышц брюшка. При сгибании брюшка эти мышцы растягиваются и рецептор активируется. Слева представлены записи электрических ответов рецептора на слабую и сильную стимуляцию. Справа указаны функции различных частей нейрона. Градуальные рецепторные токи, возникающие в чувствительной к растяжению мембране дендритов, в зоне инициации импульсов превращаются в электрические сигналы типа импульсных последовательностей или спайков.

Источником импульсных потоков в зрительном анализаторе являются ганглиозные клетки, показанные на рис. Рецепторный потенциал обычно очень мал, порядка микровольт, в то время как генераторный потенциал имеет порядок десятков милливольт, то есть в 100 и 1000 раз больше. Существенно, что рецепторный потенциал может измениться по величине в значительных пределах в десятки и сотни раз. При этом частота следования импульсов генераторного нейрона должна увеличиться пропорционально интенсивности раздражения, что следует из экспериментальных данных.

Каким образом достигаются такие замечательные свойства генераторных нейронов? Обычные нейроны, имеющие порог порядка 10 мв на такие подвиги не способны. Изучение этих явлений показало, что они могут достигаться в системах с самоорганизованной критичностью благодаря режиму вблизи порога самовозбуждения системы или вблизи точки бифуркации. Существенно, что для устойчивости таких режимов в начальных условиях требуется еще и отрицательная нелинейная обратная связь. Интересно отметить, что околопороговый режим усиления электрических колебаний широко использовался в начале развития радиотехники для построения регенеративных и сверх регенеративных приемников. В одном каскаде такого приемника достигалось усиление в миллион и более раз [4].

Все эти необычные и казалось, несовместимые свойства достигаются в биологических системах, взявших принцип самоорганизованной критичности на вооружение в ходе эволюции. При использовании нейрона в околопороговом режиме возможна синхронизация, реализующая генерацию импульсных потоков с очень низким порогом возбуждения. Уменьшение порога возбуждения за счет положительной обратной связи иллюстрируется рис. 6 слева.

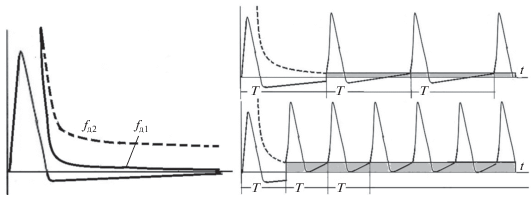
На рисунке 6 слева показаны значения порогов возбуждения в обычном случае ${{f}_{{{\text{д2}}}}}(t)$ и при увеличенной обратной связи ${{f}_{{{\text{д1}}}}}(t).$ Уменьшение порога возбуждения позволяет реализовать эффективное увеличение частоты возбуждения при увеличении амплитуды входного импульса при линейно возрастающем динамическом пороге ${{f}_{{{\text{д1}}}}}(t).$ Этот случай иллюстрируется на рис. 6 справа. Из рисунка видно, что при увеличении амплитуды возбуждения период генерируемой импульсной последовательности уменьшается, частота соответственно возрастает.

Предлагаемая математическая модель позволяет реализовать периодические последовательности нейроподобных импульсов, являющихся релаксационными колебаниями. Возможна генерация нейронных спайков, то есть серии импульсов любой заранее заданной структуры. Модель позволяет реализовать отклики с частотой следования импульсов пропорциональной интенсивности входного рецепторного потенциала.

Отметим особенности численной реализации аксиоматической модели. Используется алгебраическая аппроксимация “быстрой” и “медленной” фаз релаксационного колебания, динамического порога и внешний аппроксимирующий сигнал в виде коротких импульсов. С прикладной точки зрения такая аппроксимация синхронизирующего сигнала является достаточно адекватной, поскольку в реальных приложениях (например, при синхронизации нейронных ансамблей) синхронизация релаксационных автоколебаний производится также релаксационным колебанием в виде коротких нервных импульсов. При численной реализации выделение $\varepsilon $-почти-периодов равномерной почти-периодической функции, получаемой в результате синхронизации, осуществляется путем выделения частного от деления текущего времени процесса на период синхронизирующего колебания с помощью встроенной процедуры языка Matlab7 $\bmod (t,{{T}_{c}})$ и затем выделения остатка $R = t - \bmod (t,{{T}_{c}}).$

Достоинством предлагаемой математической модели является возможность качественного анализа на основе точных аналитических решений режимов преобразования в потоки импульсов. В то же время имеются возможность построения конкретных режимов в вычислительном эксперименте малозатратным по времени.

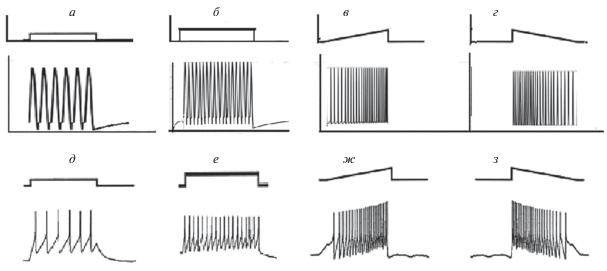
Замечательные экспериментальные результаты были получены в работе Ming-Li Zhao и Chun-Fang Wu при воздействии на нейрон of Drosophila сигналами различной формы: прямоугольными с различной амплитудой; линейно-возрастающими и линейно-убывающими [17]. Эти экспериментальные результаты приведены на рис. 7 (д, е, ж, з). Авторы отмечают, что влияние аналогичного воздействия на нейроны мозга является практически идентичным.

Существенным свойством преобразования рецепторного потенциала в генераторный является свойство линейной зависимости частоты следования импульсов от интенсивности раздражения. На рис. 8 показано изменение во времени частоты нервных импульсов в афферентном волокне от силы тока.

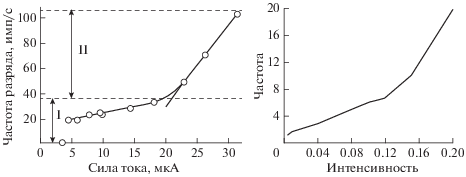
На графике зависимости частоты разряда нейрона от амплитуды стимулирующего тока, полученном экспериментально, выделяются два участка, названные первичным (I) и вторичным (II) диапазонами частоты разряда. Полученные результаты показывает то, что частота импульсации возрастает при увеличении интенсивности раздражения.

ЗАКЛЮЧЕНИЕ

Исследовано управление системой с СОК в области, окружающей точку бифуркации с использованием нелинейной отрицательной обратной связи для стабилизации. Выявлено существование замечательных свойств режимов СОК вблизи критической точки – точки бифуркации: возможность значительного повышения чувствительности и избирательности системы, возможности ускоренного развития.

Разработан математический метод исследования режимов вблизи критической точки – точки бифуркации. Это режимы пороговой синхронизации релаксационной автоколебательной системы. Предложен точный аналитический метод решения уравнений пороговой синхронизации, основанный на модификации метода Винера–Розенблюта с использованием свойств равномерных почти-периодических функций. В качестве примеров исследована работа СОК вблизи точки бифуркации при генерации потоков импульсов генераторными нейронами в физиологических сенсорных системах. Приведен пример исследования технической системы радиоприемных устройств типа регенератора и сверхрегенераторов, обеспечивающих значительное усиление и высокую избирательность благодаря пороговому режиму работы вблизи критической точки бифуркации.