Известия РАН. Серия физическая, 2022, T. 86, № 2, стр. 165-169
К молекулярно-статистической теории ферромагнитных жидкокристаллических суспензий
Д. А. Петров *
Федеральное государственное автономное образовательное учреждение высшего образования
“Пермский государственный национальный исследовательский университет”
Пермь, Россия
* E-mail: petrovda@bk.ru
Поступила в редакцию 20.09.2021
После доработки 11.10.2021
Принята к публикации 22.10.2021
- EDN: VEHXAT
- DOI: 10.31857/S0367676522020235
Аннотация
Рассмотрена молекулярно-статистическая теория среднего поля суспензий анизометричных магнитных частиц в нематических жидких кристаллах. Изучены температурные зависимости параметров порядка системы. Показано, что в зависимости от температуры суспензия может находиться в одной из фаз: изотропная жидкость, антиферромагнитный нематик или ферромагнитный нематик.
В 2013 г. была опубликована статья [1], в которой анонсировалось успешное получение ферромагнитных жидких кристаллов (ЖК). Такие композитные материалы представляют собой разбавленные суспензии коллоидных магнитных частиц в нематическом ЖК с отличной от нуля результирующей намагниченностью в отсутствие внешнего магнитного поля. Несмотря на то, что ферромагнитные ЖК были теоретически предсказаны более полувека назад [2], их экспериментальная реализация осуществлена лишь относительно недавно [3‒6]. Причина в том, что ранее использованные в качестве примеси вытянутые магнитные частицы обладают большим отношением энергии магнитного диполь-дипольного взаимодействия к тепловой энергии, что приводило к появлению цепочечных агрегатов частиц [7], которые не способны образовывать спонтанное упорядочение. В работе [1] эта проблема была решена путем использования в качестве примеси дискообразных магнитных частиц с гомеотропным сцеплением ЖК с поверхностью диска. Несмотря на более чем полувековую историю изучения ЖК композитов дипольных частиц лишь недавно была предложена молекулярно-статистическая теория [8, 9], в рамках которой удалось описать появление спонтанной намагниченности ЖК суспензий. Настоящая работа посвящена дальнейшему развитию этой теории.
Рассмотрим однородную однодоменную ЖК-суспензию как бинарную смесь ${{N}_{n}}$ мезогенных молекул и ${{N}_{p}}$ анизометричных частиц. Ориентацию отдельной стержнеобразной молекулы ЖК и дискообразной частицы соответственно будем описывать симметричными бесследовыми тензорами второго ранга
(1)
$\nu _{{ik}}^{\alpha } = \sqrt {\frac{3}{2}} \left( {{{\nu }_{{\alpha i}}}{{\nu }_{{\alpha k}}} - \frac{1}{3}{{\delta }_{{ik}}}} \right),\,\,\,e_{{ik}}^{\beta } = \sqrt {\frac{3}{2}} \left( {{{e}_{{\beta i}}}{{e}_{{\beta k}}} - \frac{1}{3}{{\delta }_{{ik}}}} \right).$Согласно работе [1] предположим, что поверхность дискообразных магнитных частиц гомеотропно сцеплена с ЖК-матрицей, а магнитные моменты ${{\vec {\mu }}_{\beta }} = \mu {{\vec {e}}_{\beta }}$ направлены ортогонально плоскостям дисков ($\mu $ – величина магнитного момента). В случае, когда ЖК находится в мезоморфном состоянии, магнитные моменты частиц спонтанно упорядочиваются. Для описания спонтанной намагниченности частиц введем векторный параметр порядка
(2)
$\vec {M} = \frac{1}{{\mu {{N}_{p}}}}\sum\limits_{\beta = 1}^{{{N}_{p}}} {{{{\vec {\mu }}}_{\beta }}} .$Между тонким диском с гомеотропным сцеплением и тонким стержнем с планарным сцеплением с ЖК-матрицей существует топологическое сходство. Таким образом, под планарным сцеплением будем подразумевать ${{\vec {\nu }}_{\alpha }}{\text{||}}{{\vec {e}}_{\beta }}.$
Макроскопические тензоры ориентации компонентов суспензии и векторный параметр порядка соответственно могут быть получены в результате статистического усреднения тензоров $\nu _{{ik}}^{\alpha },$ $e_{{ik}}^{\beta }$ и вектора ${{\vec {e}}_{\beta }}.$ Полагая, что в отсутствие внешнего магнитного поля главные оси нематического порядка ЖК и частиц совпадают (планарное сцепление), то макроскопические тензоры ориентации, получаемые путем статистического усреднения тензоров (1), и векторный параметр порядка (2) могут быть представлены через один вектор – директор $\vec {n}{\text{:}}$
(3)
$\begin{gathered} {{\eta }_{{ik}}} = \left\langle {\nu _{{ik}}^{\alpha }} \right\rangle = \sqrt {\frac{3}{2}} \eta \left( {{{n}_{i}}{{n}_{k}} - \frac{1}{3}{{\delta }_{{ik}}}} \right), \\ {{S}_{{ik}}} = \left\langle {e_{{ik}}^{\beta }} \right\rangle = \sqrt {\frac{3}{2}} S\left( {{{n}_{i}}{{n}_{k}} - \frac{1}{3}{{\delta }_{{ik}}}} \right), \\ \vec {M} = \left\langle {{{{\vec {e}}}_{\beta }}} \right\rangle = M\vec {n}. \\ \end{gathered} $(4)
$\begin{gathered} \eta = \left\langle {{{{\text{P}}}_{2}}(\vec {n} \cdot \vec {\nu })} \right\rangle = \int {{{{\text{P}}}_{2}}(\vec {n} \cdot \vec {\nu }){{w}_{n}}(\vec {n} \cdot \vec {\nu })} d\vec {\nu }, \\ S = \left\langle {{{{\text{P}}}_{2}}(\vec {n} \cdot \vec {e})} \right\rangle = \int {{{{\text{P}}}_{2}}(\vec {n} \cdot \vec {e}){{w}_{p}}(\vec {n} \cdot \vec {e})} d\vec {e}, \\ M = \left\langle {{{{\text{P}}}_{1}}(\vec {n} \cdot \vec {e})} \right\rangle = \int {{{{\text{P}}}_{1}}(\vec {n} \cdot \vec {e}){{w}_{p}}(\vec {n} \cdot \vec {e})} d\vec {e}. \\ \end{gathered} $Согласно [8] запишем выражение для плотности свободной энергии ЖК суспензии анизометричных ферромагнитных частиц
(5)
$\begin{gathered} F\frac{{{{\nu }_{n}}}}{{\lambda V}} = - \frac{1}{2}y_{n}^{2}{{\eta }_{{ik}}}{{\eta }_{{ik}}} + {{y}_{n}}\tau \left\langle {\ln {{w}_{n}}} \right\rangle + {{y}_{p}}\gamma \tau \left\langle {\ln {{w}_{p}}} \right\rangle - \\ - \,\,{{y}_{n}}{{y}_{p}}\gamma \omega {{\eta }_{{ik}}}{{S}_{{ik}}} - {{y}_{n}}{{y}_{p}}\gamma {{\omega }_{m}}{{\eta }_{{ik}}}{{M}_{i}}{{M}_{k}}. \\ \end{gathered} $В выражении (5) первые два слагаемых отвечают за плотность свободной энергии нематической дисперсионной среды. Третье слагаемое – это энтропийный вклад ансамбля примесных частиц. Четвертое слагаемое имеет немагнитное ван-дер-ваальсово происхождение и позволяет учесть ориентационную связь между молекулами и анизометричными частицами. Последний пятый вклад учитывает связь между нематической матрицей и намагниченностью дисперсной фазы. Подобное слагаемое ранее было рассмотрено в рамках феноменологической теории Ландау–де Жена [10, 12] для описания ферромагнитного порядка примесных частиц в ЖК-матрице.
В результате вычисления всех сверток и варьирования (5) по функциям распределения ${{w}_{n}}$ и ${{w}_{p}}$ получим равновесные выражения
(6)
$\begin{gathered} {{w}_{n}} = \frac{1}{{4\pi }}\frac{{\exp \left\{ {{{\sigma }_{n}}{{{\cos }}^{2}}{{\theta }_{n}}} \right\}}}{{g\left( {{{\sigma }_{n}},0} \right)}}, \\ {{w}_{p}} = \frac{1}{{4\pi }}\frac{{\exp \left\{ {{{\sigma }_{p}}{{{\cos }}^{2}}{{\theta }_{p}} + \zeta \cos {{\theta }_{p}}} \right\}}}{{g\left( {{{\sigma }_{p}},\zeta } \right)}}, \\ \end{gathered} $(7)
$\begin{gathered} {{\sigma }_{n}} = \frac{3}{{2\tau }}\left[ {{{y}_{n}}\eta + {{y}_{p}}\gamma \omega S + \frac{{\sqrt 6 }}{3}{{y}_{p}}\gamma {{\omega }_{m}}{{M}^{2}}} \right], \\ {{\sigma }_{p}} = \frac{3}{{2\tau }}{{y}_{n}}\omega \eta ,\,\,\,\,\zeta = \frac{{2\sqrt 6 }}{{3\tau }}{{y}_{n}}{{\omega }_{m}}\eta M \\ \end{gathered} $и определена функция
(8)
$g(\sigma ,\zeta ) = \frac{1}{2}\int\limits_{ - 1}^1 {\exp \left\{ {\sigma {{x}^{2}} + \zeta x} \right\}} dx.$Подстановка (6) в (4) позволяет получить уравнения ориентационного равновесия:
(9)
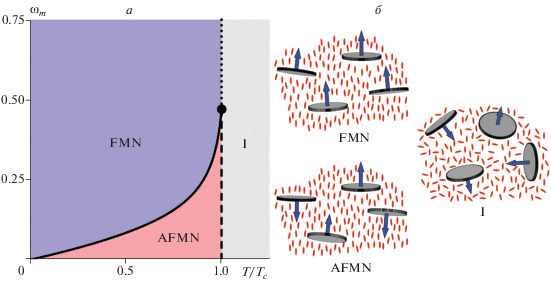
$\begin{gathered} \eta = \frac{3}{2}\frac{{\partial \ln g({{\sigma }_{n}},0)}}{{\partial {{\sigma }_{n}}}} - \frac{1}{2},\,\,\,\,S = \frac{3}{2}\frac{{\partial \ln g({{\sigma }_{p}},\zeta )}}{{\partial {{\sigma }_{p}}}} - \frac{1}{2}, \\ M = \frac{{\partial \ln g({{\sigma }_{p}},\zeta )}}{{\partial \zeta }}. \\ \end{gathered} $Система уравнений (9) допускает несколько типов решений, отвечающих различным фазовым состояниям суспензии. Первое решение соответствует высокотемпературной изотропной фазе (I), для которой $\eta = S = M = 0.$ Второе решение отвечает антиферромагнитной нематической фазе (AFMN) $\eta > 0,$ $S > 0$ и $M = 0,$ а третье – ферромагнитной нематической фазе (FMN), для которой $\eta > 0,$ $S > 0$ и $M \ne 0.$ На рис. 1а представлена диаграмма фазовых состояний суспензии в терминах приведенной температуры ${T \mathord{\left/ {\vphantom {T {{{T}_{c}}}}} \right. \kern-0em} {{{T}_{c}}}}$ (${{T}_{c}}$ – температура равновесного фазового перехода между нематической и изотропной фазами для обычного ЖК) и параметра среднего поля ${{\omega }_{m}},$ отвечающего за интенсивность магнитного взаимодействия молекул ЖК с примесными частицами. В расчетах использовались значения параметров из работ [8], являющиеся типичными для ферромагнитных ЖК суспензий [1] ${{y}_{p}} = 3 \cdot {{10}^{{ - 4}}},$ $\gamma = 2.107 \cdot {{10}^{{ - 5}}},$ $\omega = 1.2,$ $\lambda = 1.934 \cdot {{10}^{{ - 20}}}$ Дж и ${{T}_{c}} = 308.4$ К. На рис. 1б схематически изображены FMN, AFMN и I фазы, где стрелками обозначены направления магнитных моментов дискообразных частиц. Из рис. 1а видно, что при параметрах ${{\omega }_{m}} > \omega _{m}^{T} = 0.4703,$ где $\omega _{m}^{T}$ отвечает тройной точке I-AFMN-FMN (черный круг на рис. 1а), в суспензии возможен прямой переход из изотропной фазы в упорядоченное ферромагнитное состояние, которому отвечает фазовый переход первого рода (пунктирная прямая). Для ${{\omega }_{m}} < \omega _{m}^{T}$ переход из высокотемпературной I фазы сначала происходит в AFMN состояние и лишь с дальнейшим уменьшением температуры появляется спонтанная намагниченность и сиcтема переходит в FMN фазу. Этим переходам соответственно отвечают фазовые переходы первого и второго рода (штриховая и сплошная кривая). Здесь стоит отметить, что из-за малой объемной доли примеси и относительно больших размеров частиц по сравнению с молекулами ЖК (${{y}_{p}} \ll 1$ и $\gamma \ll 1$) температуры ${{T}_{{FI}}}$ и ${{T}_{{AI}}}$ переходов между I фазой и упорядоченными FMN и AFMN фазами соответственно почти не зависят от параметра ${{\omega }_{m}}$ и очень слабо отличаются от ${{T}_{c}}.$ Для построения фазовой диаграммы значение ${{T}_{{FI}}}$ (${{T}_{{AI}}}$) определялось путем численного решения системы уравнений (9) совместно с условием равенства свободных энергий соответственно упорядоченной FMN (AFMN) и изотропной фаз.
Рис. 1.
Диаграмма ориентационных фаз суспензии в терминах приведенной температуры ${T \mathord{\left/ {\vphantom {T {{{T}_{c}}}}} \right. \kern-0em} {{{T}_{c}}}}$ и параметра сцепления ${{\omega }_{m}}$ (а); схематическое представление изотропной I, антиферромагнитной нематической AFMN и ферромагнитной нематической FMN фаз (б).
На рис. 2 и 3 представлены температурные зависимости параметров порядка ЖК и ансамбля частиц, полученные в результате численного решения системы уравнений (9) соответственно для ${{\omega }_{m}} = 0.37 < \omega _{m}^{T}$ и ${{\omega }_{m}} = 0.57 > \omega _{m}^{T}.$ На этих рисунках сплошные кривые соответствуют термодинамически устойчивым состояниям, а пунктирные – неустойчивым и метастабильным состояниям. Вертикальные отрезки прямых отвечают равновесным переходам первого рода FMN-I или AFMN-I. Из рис. 2а видно, что в соответствии с фазовой диаграммой (см. рис. 1а) с понижением температуры I фаза теряет устойчивость и при $T = {{T}_{{AI}}}$ происходит переход первого рода в AFMN фазу, для которой температурные зависимости параметров порядка $\eta \equiv {{\eta }_{A}}$ и $S \equiv {{S}_{A}}$ ($M \equiv 0$) определяются из совместного решения первых двух уравнений системы (9). С дальнейшим понижением температуры при $T = {{T}_{{FA}}},$ где ${{{{T}_{{FA}}}} \mathord{\left/ {\vphantom {{{{T}_{{FA}}}} {{{T}_{c}}}}} \right. \kern-0em} {{{T}_{c}}}} = {\text{0}}{\text{.9776,}}$ в суспензии появляется спонтанная намагниченность и происходит переход в FMN фазу (см. рис. 2б). Зависимости параметров порядка от температуры в этой фазе $\eta \equiv {{\eta }_{F}},$ $S \equiv {{S}_{F}}$ и $M \ne 0$ определяются путем решения всех уравнений системы (9). Из рис. 2а видно, что значения нематического параметра порядка ансамбля частиц ${{S}_{F}} > {{S}_{A}}$ (на рис. 2а значениям ${{S}_{A}}$ в FMN фазе отвечает пунктирная кривая), в то время как для ЖК подсистемы значения ${{\eta }_{F}}$ и ${{\eta }_{A}}$ слабо отличаются и ложатся на одну кривую. Температура перехода FMN–AFMN может быть определена в результате решения системы уравнений (9) при $M = 0$ совместно с условием потери устойчивости FMN фазы ${{\left. {{{{{\partial }^{2}}F} \mathord{\left/ {\vphantom {{{{\partial }^{2}}F} {\partial {{M}^{2}}}}} \right. \kern-0em} {\partial {{M}^{2}}}}} \right|}_{{M = \,0}}} = 0,$ которое имеет вид
(10)
$\tau = {{({2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3})}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{y}_{n}}{{\omega }_{m}}\eta (2S + 1).$Рис. 2.
Температурные зависимости нематических параметров порядка компонентов суспензии (а) и магнитного параметра порядка частиц (б) для ${{\omega }_{m}} < \omega _{m}^{T}.$ Последовательность переходов FMN-AFMN-I. Здесь ${{T}_{{FA}}}$ – температура перехода между FMN и AFMN фазами, ${{T}_{{AI}}}$ – температура перехода между AFMN и I фазами, ${{T}_{ * }}$ – температура абсолютной неустойчивости I фазы относительно перехода в AFMN состояние. Сплошные линии – термодинамически устойчивые ветви, пунктирные – метастабильные и неустойчивые.
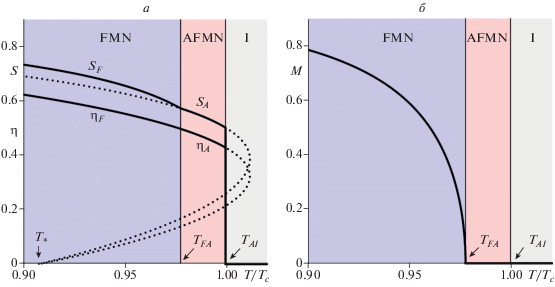
Рис. 3.
Температурные зависимости нематических параметров порядка компонентов суспензии (а) и магнитного параметра порядка частиц (б) для ${{\omega }_{m}} > \omega _{m}^{T}.$ Прямой переход FMN-I. Здесь ${{T}_{{FI}}}$ – температура перехода между FMN и I фазами, ${{T}_{ * }}$ – температура абсолютной неустойчивости I фазы относительно перехода в AFMN состояние. Сплошные линии – термодинамически устойчивые ветви, пунктирные – метастабильные и неустойчивые.
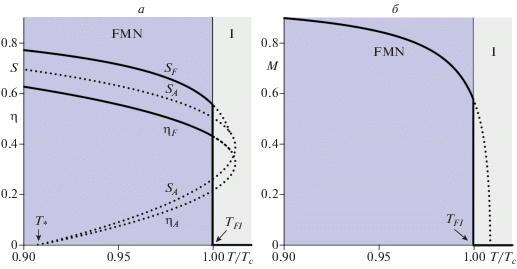
При S = 0 этот результат совпадает с тем, что был ранее получен в работе [9].
На рис. 3 рассмотрен случай, когда в суспензии происходит прямой переход первого рода из изотропной жидкости в упорядоченную ферромагнитную фазу, минуя антиферромагнитное состояние. Во всем температурном диапазоне решения, отвечающие AFMN фазе ηA, SA и M = 0, являются термодинамически неустойчивыми по отношению либо к I фазе при $T > {{T}_{{FI}}},$ либо к FMN фазе при $T < {{T}_{{FI}}}.$
На рис. 2 и 3 также присутствует температура абсолютной неустойчивости изотропной фазы по отношению к переходу в AFMN состояние ${{T}_{ * }}.$ Согласно работе [11] при ${{{{y}_{p}}\gamma {{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{y}_{p}}\gamma {{\omega }^{2}}} {{{y}_{n}}}}} \right. \kern-0em} {{{y}_{n}}}} \ll 1$ выражение для этой температуры имеет вид
(11)
${{T}_{ * }} = \frac{{\lambda {{y}_{n}}}}{{5{{k}_{b}}}}\left( {1 + \frac{{{{y}_{p}}\gamma {{\omega }^{2}}}}{{{{y}_{n}}}}} \right)$и для рассматриваемых значений материальных параметров с большой степенью точности совпадает с точкой Кюри для беспримесного ЖК ${{\tau }_{ * }} = {{{{k}_{b}}{{T}_{ * }}} \mathord{\left/ {\vphantom {{{{k}_{b}}{{T}_{ * }}} \lambda }} \right. \kern-0em} \lambda } \approx 0.2.$
Подводя итог, нужно отметить, что предложенная молекулярно-статистическая теория среднего поля суспензий анизометричных ферромагнитных частиц в ЖК позволяет описать последовательность переходов изотропная жидкость–антиферромагнитный нематик–ферромагнитный нематик или один прямой переход из изотропной фазы в ферромагнитное нематическое состояние. Представленные в настоящей работе фазовые диаграммы и температурные зависимости параметров порядка согласуются с результатами, полученными в рамках феноменологической теории Ландау–де Жена [10, 12]. Преимущество предлагаемого в статье подхода заключается в том, что он позволяет описать ориентационную и магнитную структуру ЖК композита во всей температурной области существования мезофазы, в отличие от теории Ландау–де Жена, результаты которой как известно применимы лишь в окрестности точки фазового перехода. Кроме этого, предложенная теория основывается на тензорной форме записи плотности свободной энергии (5). Это позволяет, задавая симметрию макроскопических тензоров ориентации (3), рассматривать в дальнейшем не только оптически одноосные, так и двуосные фазы.
Исследование выполнено при финансовой поддержке РФФИ (проект № 19-02-00231) и Фонда развития теоретической физики и математики “БАЗИС”. Автор выражает благодарность Павлу Васильевичу Краузину и анонимному рецензенту за ценные замечания к исходному варианту статьи.
Список литературы
Mertelj A., Lisjak D., Drofenik M., Čopič M. // Nature. 2013. V. 504. P. 237.
Brochard F., de Gennes P.G. // J. de Physique. 1970. V. 31. P. 691.
Potisk T., Svenšek D., Brand H.R. et al. // Phys. Rev. Lett. 2017. V. 119. Art. No. 097802.
Sebastián N., Osterman N., Lisjak D. et al. // Soft Matter. 2018. V. 14. P. 7180.
Sebastian N., Lisjak D., Čopič M. et al. // J. Mol. Liq. 2018. V. 267. P. 377.
Potisk T., Mertelj A., Sebastián N. et al. // Phys. Rev. E. 2018. V. 97. Art. No. 012701.
Morozov K.I. // Phys. Rev. E. 2002. V. 66. Art. No. 011704.
Petrov D.A. // Phys. Rev. E. 2020. V. 101. Art. No. 030701(R).
Петров Д.А., Скоков П.К. // Жидк. крист. и их практ. использ. 2020. Т. 20. № 4. С. 63; Petrov D.A., Skokov P.K. // Liq. Cryst. Appl. 2020. V. 20. No. 4. P. 63.
Pleiner H., Jarkova E., Müller H.-W., Brand H.R. // Magnetohydrodynamics. 2001. V. 37. No. 3. P. 254.
Захлевных А.Н., Лубнин М.С., Петров Д.А. // ЖЭТФ. 2016. Т. 150. № 5(11). С. 1041; Zakhlevnykh A.N., Lubnin M.S., Petrov D.A. // J. Exp. Theor. Phys. 2016. V. 123. No. 5. P. 908.
Khalilov T., Makarov D., Petrov D. // Crystals. 2021. V. 11. Art. No. 639.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


