Известия РАН. Серия физическая, 2022, T. 86, № 2, стр. 187-193

ВВЕДЕНИЕ

Жидкие кристаллы (ЖК) – это вещества, сочетающие в себе свойства жидкостей (текучесть) и кристаллических твердых тел (анизотропия) [1]. Одной из разновидностей ЖК являются холестерические жидкие кристаллы (ХЖК), которые помимо дальнего ориентационного порядка в расположении молекул, характеризуются спонтанной спиральностью – вращением молекул в направлении, перпендикулярном их длинным осям. Их спиральная ориентационная структура может быть обратимым образом деформирована внешним воздействием [2]. Так, постоянное [3] или вращающееся [4] магнитное поле способно индуцировать переход ориентационной структуры в однородное состояние (переход холестерик–нематик). Раскручивание спирали обеспечивается так называемым квадрупольным (диамагнитным) механизмом, связанным с воздействием поля на анизотропную матрицу ХЖК. Добавление примесных магнитных частиц планарно сцепленных с матрицей, как показано в работе [5], должно привести к уменьшению величины управляющего магнитного поля. В этом случае появляется дополнительный способ влияния на систему, обусловленный воздействием поля на магнитные моменты феррочастиц (дипольный механизм). Он линеен по напряженности поля и определяет поведение суспензии в слабых полях. Однородные ориентационные фазы в такой жидкокристаллической суспензии (с дипольным и квадрупольным механизмами воздействия) при различных формах потенциала сцепления между частицами и молекулами ЖК были изучены в работах [6–8]. В данной работе в качестве примесной подсистемы рассматриваются диамагнитные (квадрупольные) частицы, например, углеродные нанотрубки [9–14]. Анализируются возможные ориентационные фазы в суспензии квадрупольных частиц на основе ХЖК, в которые она может перейти при раскручивании спиральной структуры. Рассматривается конечное гомеотропное сцепление между подсистемами, приводящее к конкуренции между двумя квадрупольными механизмами влияния магнитного поля на суспензию.

ПОСТАНОВКА ЗАДАЧИ

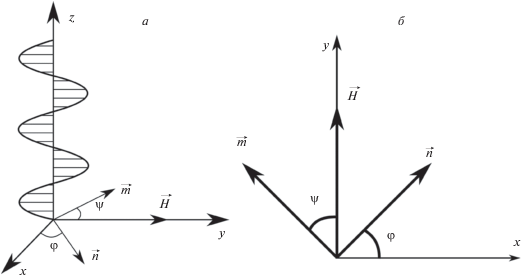
Рассмотрим неограниченный образец ЖК-суспензии диамагнитных частиц на основе холестерического жидкого кристалла (рис. 1). Внешнее магнитное поле направим перпендикулярно оси холестерической спирали: $\vec {H} = \left( {0,H,0} \right).$ В континуальном подходе особенности ориентационных переходов ЖК-суспензии могут быть изучены из условия минимума функционала полной свободной энергии $F = \int_V {{{F}_{V}}dV} ,$ ${{F}_{V}}$ – объемная плотность свободной энергии суспензии, помещенной в магнитное поле. Будем описывать ориентационную структуру суспензии с однородным распределением диамагнитных частиц в матрице (бессегрегационный предел), учитывая конечное сцепление между примесной и жидкокристаллической подсистемами. В этом случае объемная плотность будет содержать следующие вклады [15–17]:

Здесь $\vec {n}$ – директор ХЖК, ${{K}_{{11}}},$ ${{K}_{{22}}},$ ${{K}_{{33}}}$ – модули ориентационной упругости ХЖК (константы Франка), ${{q}_{0}}$ – волновое число спиральной структуры ХЖК, ${{\chi }_{a}}$ – анизотропия диамагнитной восприимчивости ХЖК, $\vec {m}$ – директор диамагнитных частиц (единичный вектор, характеризующий направление преимущественной ориентации длинных осей частиц), $\chi _{a}^{p}$ – анизотропия диамагнитной восприимчивости примесных частиц, $f$ – объемная доля диамагнитных частиц в суспензии, $W$ – поверхностная плотность энергии сцепления молекул ХЖК с частицами, которую будем считать положительной, $d$ – поперечный диаметр частицы. Слагаемое ${{F}_{1}}$ – плотность свободной энергии ориентационно-упругих деформаций ХЖК (потенциал Франка), вклады ${{F}_{2}}$ и ${{F}_{3}}$ описывают квадрупольное взаимодействие ЖК‑матрицы и примесных частиц с магнитным полем $\vec {H},$ ${{F}_{4}}$ – объемная плотность энергии ориентационного взаимодействия ЖК-матрицы и диамагнитных частиц.

В отсутствие внешнего магнитного поля $\vec {H}$ векторные поля $\vec {n}$ и $\vec {m}$ являются пространственно-однородными в плоскости xOy, а вследствие положительности поверхностной плотности энергии $W$ они будут направлены ортогонально друг другу ($\vec {n} \bot \vec {m}$). Кроме того, в пространстве они непрерывно поворачиваются вокруг оси холестерической спирали с шагом ${{p}_{0}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{q}_{0}}}}} \right. \kern-0em} {{{q}_{0}}}}.$ Включение магнитного поля $\vec {H} = \left( {0,H,0} \right)$ деформирует исходную ориентационную структуру суспензии в плоскости, ортогональной оси спирали, что позволяет искать поля директоров в следующем виде:

Учитывая соотношения (2) и однородное распределение частиц $f = {{f}_{0}} \equiv \frac{{N{{\nu }_{p}}}}{V}$ (где $N$ – число частиц, ${{\nu }_{p}}$ – объем частицы, $V$ – объем образца), безразмерная объемная плотность свободной энергии суспензии примет вид:

где $\zeta = {{q}_{0}}z$ – безразмерная координата, $h = {H \mathord{\left/ {\vphantom {H {{{q}_{0}}\sqrt {{{{{\chi }_{a}}} \mathord{\left/ {\vphantom {{{{\chi }_{a}}} {{{K}_{{22}}}}}} \right. \kern-0em} {{{K}_{{22}}}}}} }}} \right. \kern-0em} {{{q}_{0}}\sqrt {{{{{\chi }_{a}}} \mathord{\left/ {\vphantom {{{{\chi }_{a}}} {{{K}_{{22}}}}}} \right. \kern-0em} {{{K}_{{22}}}}}} }}$ – безразмерная напряженность магнитного поля, $\gamma = {{\chi _{a}^{p}{{f}_{0}}} \mathord{\left/ {\vphantom {{\chi _{a}^{p}{{f}_{0}}} {{{\chi }_{a}}}}} \right. \kern-0em} {{{\chi }_{a}}}}$ – отношение удельных анизотропий диамагнитных восприимчивостей примесных частиц и ХЖК, $\sigma = {{W{{f}_{0}}} \mathord{\left/ {\vphantom {{W{{f}_{0}}} {\left( {d{{K}_{{22}}}q_{0}^{2}} \right)}}} \right. \kern-0em} {\left( {d{{K}_{{22}}}q_{0}^{2}} \right)}}$ – безразмерная энергия сцепления между ХЖК-матрицей и диамагнитными частицами.

Полагая анизотропию холестерика χ_a ≈ 10^–6–10^–7 и примесных частиц (нанотрубок) $\chi _{a}^{p} \approx {{10}^{{ - 5}}} - {{10}^{{ - 4}}},$ а среднюю концентрацию примеси в суспензии ${{f}_{0}} \approx {{10}^{{ - 3}}},$ получаем диапазон значений параметра $\left| \gamma \right| \approx 0.1--1.$ Отрицательное значение $\gamma $ может быть достигнуто за счет отрицательной диамагнитной анизотропии ХЖК или диамагнитной примеси. Будем считать модуль упругости Франка ${{K}_{{22}}} \approx {{10}^{{ - 12}}}$ Н, волновое число спирали ${{q}_{0}} \approx {{10}^{2}}--{{10}^{4}},$ энергию сцепления между молекулами ЖК и частицами примеси $W \approx {{10}^{{ - 7}}}--{{10}^{{ - 3}}}$ Н/м. Таким образом, значения безразмерной напряженности магнитного поля – $h \approx {{10}^{{ - 2}}}.$ Для примесных частиц диаметром $d \approx 20--50$ нм значение параметра сцепления может варьироваться в пределах $\sigma \approx 10--{{10}^{5}}.$ При этом для примесных частиц должно выполняться условие ${l \mathord{\left/ {\vphantom {l d}} \right. \kern-0em} d} \geqslant 10,$ где $l$ – длина частицы [5, 7, 16].

Минимизация по углам $\varphi $ и $\psi $ свободной энергии суспензии с учетом (3) приводит к уравнениям равновесия:

описывающим ориентационное поведение ЖК-суспензии в рассматриваемой геометрии задачи. В раскрученной ориентационной фазе углы поворота директоров не зависят от пространственных координат, соответственно слагаемое, содержащее вторую производную угла $\varphi ,$ будет равно нулю, и система (4)–(5) упростится следующим образом:

Система (6)–(7) определяет ориентационные состояния суспензии в раскрученной фазе с углами ${{\varphi }_{0}},$ ${{\psi }_{0}},$ и имеет три решения, отвечающие следующим однородным фазам: гомеотропной, угловой и планарной. При этом в зависимости от значения параметра $\gamma $ реализуется один из двух вариантов гомеотропной фазы с различной ориентацией директоров относительно направления внешнего магнитного поля.

ПОРОГОВЫЕ ПОЛЯ

Первое решение системы уравнений (6) и (7), ${{\varphi }_{0}} = {{\psi }_{0}} = 0,$ соответствует гомеотропной фазе (I) с ортогональными друг другу директорами $\vec {n}$ и $\vec {m},$ причем директор примесных частиц $\vec {m}$ ориентируется по полю $\vec {H},$ а директор ЖК $\vec {n}$ – ортогонально ему. Это решение существует, если удельная анизотропия диамагнитной восприимчивости примеси больше, чем анизотропия восприимчивости ЖК подсистемы, что соответствует параметру $\gamma > 1.$ Разложение уравнений (6)–(7) по малым отклонениям углов ориентации директоров вблизи нулевых значений ${{\varphi }_{0}}$ и ${{\psi }_{0}}$ приводит к линейной системе уравнений, из условия существования нетривиальных решений которой получается следующее значение порогового поля:

Второе решение системы (6)–(7), φ₀ = ψ₀ = = π/2, определяет гомеотропную фазу (II), в которой директор ЖК $\vec {n}$ ориентируется параллельно приложенному полю $\vec {H}.$ Такой случай реализуется, если параметр, характеризующий отношение удельных анизотропий восприимчивости $\gamma < 1.$ Значение поля перехода в данную ориентационную фазу

Кроме того, система (6)–(7) допускает и нетривиальные решения, отвечающие угловой фазе (III), в которой ${{\varphi }_{0}}$ и ${{\psi }_{0}}$ не равны 0 или $\frac{\pi }{2},$ а подчиняются следующим распределениям:

Наконец, возможно решение ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ и ${{\psi }_{0}} = 0$ для планарной ориентационной фазы (IV) с параллельными полю векторами $\vec {n}$ и $\vec {m}.$ Значение порогового поля перехода в эту фазу

Границы указанных однородных ориентационных состояний раскрученной суспензии изображены на фазовых диаграммах рис. 2. Кривые, определяемые формулами (8), (9), (12), делят плоскость $h - \gamma $ (см. рис. 2а) на четыре области, соответствующие фазам I–IV. В слабых магнитных полях устойчива гомеотропная фаза. При отношении удельных анизотропий диамагнитных восприимчивостей подсистем $\gamma > 1$ с ростом напряженности при $h \geqslant {{h}_{{ \bot 1}}}$ (8) система в раскрученном состоянии будет находиться в гомеотропной фазе (I). В этом случае поле ориентирует суспензию таким образом, что директор диамагнитных частиц $\vec {m}$ поворачивается в направлении поля $\vec {H}$: $\vec {m}\parallel \vec {H} \bot \vec {n}.$ В этой фазе упорядочение осуществляется квадрупольным механизмом примесной подсистемы. Если параметр $\gamma < 1,$ т.е. удельная анизотропия магнитной восприимчивости холестерика больше, чем у диамагнитных частиц, то при $h \geqslant {{h}_{{ \bot 2}}}$ (9) система перейдет в гомеотропную фазу (II). В этом случае директор ЖК $\vec {n}$ ориентирован вдоль поля $\vec {H}{\text{:}}$ $\vec {n}\parallel \vec {H} \bot \vec {m},$ – упорядочение в системе осуществляется квадрупольным механизмом жидкокристаллической матрицы.

При напряженностях магнитного поля h_⊥ < h < < h_|| раскрученное состояние суспензии будет соответствовать угловой фазе (III), в которой угол между директорами лежит в интервале значений от 0 до ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$ В данной фазе происходит изменение условий сцепления (от гомеотропных к планарным) между примесной и жидкокристаллической подсистемами: при увеличении напряженности оба директора стремятся выстроиться вдоль поля. При $h \geqslant {{h}_{{||}}}$ реализуется параллельная ориентация директоров $\vec {n}\left\| {\vec {H}} \right\|\vec {m},$ соответствующая планарной ориентационной фазе (IV). Здесь поле ${{h}_{{||}}}$ можно интерпретировать как поле насыщения. Ширина переходной области ${{h}_{ \bot }} - {{h}_{{||}}},$ т.е. ширина угловой фазы (III), существенно зависит от параметра $\gamma .$ Наибольшая ширина достигается при $\gamma = 1,$ когда равны удельные анизотропии восприимчивостей обеих подсистем. В случае малых $\gamma ,$ например, при малой концентрации примесной фазы, вклад диамагнитных частиц становится несущественным, и необходимо приложить большое поле, чтобы нарушить гомеотропную ориентацию директоров – график зависимости $h\left( \gamma \right)$ неограниченно возрастает при $\gamma = 0$ (см. рис. 2а). Устремив $\gamma $ к бесконечности в выражениях (8) и (12), получаем одинаковые асимптотики для критических полей ${{h}_{{ \bot 1}}}$ и ${{h}_{{||}}}{\text{:}}$

поэтому при увеличении параметра $\gamma $ ширина угловой фазы (III) стремится к нулю, а значит переход из гомеотропной фазы (I) в планарную фазу (IV) будет происходить скачком.

Как видно из рис. 2б, увеличение энергии сцепления $\sigma $ между ХЖК и диамагнитными частицами приводит к повышению пороговых полей ${{h}_{ \bot }}$ и ${{h}_{{||}}}.$ При фиксированной энергии сцепления $\sigma $ с увеличением поля $h$ в раскрученном состоянии суспензии реализуется последовательность ориентационных переходов: гомеотропная фаза (I или II)–угловая фаза (III)–планарная фаза (IV). В зависимости от величины $\gamma $ в этой последовательности реализуется одна из возможных гомеотропных фаз.

ОРИЕНТАЦИОННАЯ СТРУКТУРА

Решая систему уравнений (6)–(7) для различных значений напряженности поля h, энергии сцепления $\sigma $ и параметра анизотропии $\gamma $ можно проследить изменение углов ${{\varphi }_{0}}$ и ${{\psi }_{0}}$ в рассмотренных выше фазах. Так, фиксируя $\sigma $ и $\gamma ,$ с изменением поля $h$ реализуется поведение углов, представленное на рис. 3а и 3б. Точкам излома на графиках соответствуют критические значения магнитного поля ${{h}_{{ \bot 1}}}$ (8), ${{h}_{{ \bot 2}}}$ (9) и ${{h}_{{||}}}$ (12). Заметим, что при каком-либо фиксированном значении параметра $\gamma $ сразу обе гомеотропные фазы (I и II) не могут быть получены за счет изменения напряженности магнитного поля h. Первое критическое поле ${{h}_{{ \bot 1}}},$ разделяющее фазы I и III, существует при $\gamma > 1,$ а второе ${{h}_{{ \bot 2}}},$ разделяющее фазы II и III, существует только при $\gamma < 1.$ При $\gamma > 1$ с ростом поля суспензия в раскрученном состоянии проходит фазы I–III–IV (рис. 3а), а для $\gamma < 1,$ т. е. при малой концентрации или анизотропии диамагнитной восприимчивости примесных частиц, последовательно сменяются фазы II, III и IV (рис. 3б).

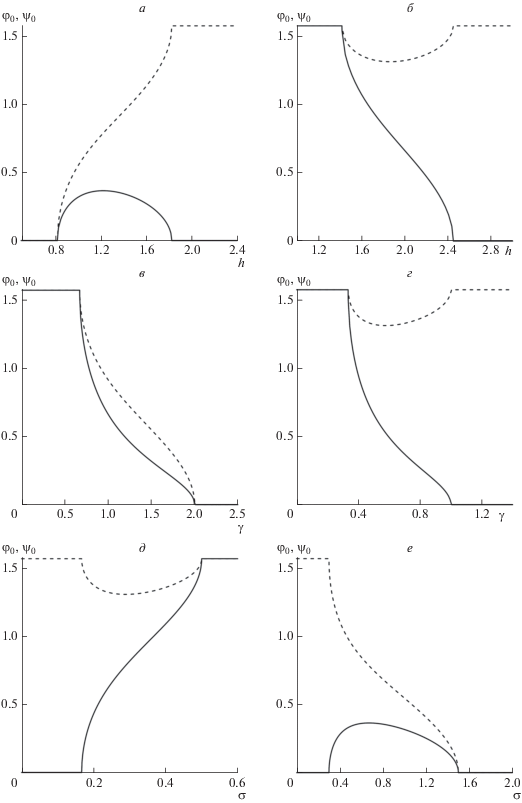
Изменение углов ${{\varphi }_{0}}$ и ${{\psi }_{0}}$ от параметра анизотропии диамагнитной восприимчивости $\gamma $ в постоянном поле $h$ для энергии сцепления $\sigma $ представлено на рис. 3в и рис. 3г. Критические параметры анизотропии ${{\gamma }_{{ \bot 1}}},$ ${{\gamma }_{{ \bot 2}}}$ и ${{\gamma }_{{||}}},$ определяющие границы между фазами, могут быть выражены непосредственно из соотношений (8), (9) и (12). При напряженностях магнитного поля ниже ${{h}_{*}}$ (13) поведение углов ${{\varphi }_{0}}$ и ${{\psi }_{0}},$ отвечающее последовательности фаз II–III–I, показано на рис. 3в. При $h > {{h}_{*}}$ с увеличением $\gamma $ реализуется последовательность фаз II–III–IV, соответствующие зависимости углов ${{\varphi }_{0}}\left( \gamma \right)$ и ${{\psi }_{0}}\left( \gamma \right)$ представлены на рис. 3г. Зависимости углов ${{\varphi }_{0}}$ и ${{\psi }_{0}}$ от энергии сцепления $\sigma $ между подсистемами изображены на рис. 3д и рис. 3е. Критические значения ${{\sigma }_{{ \bot 1}}},$ ${{\sigma }_{{ \bot 2}}}$ и ${{\sigma }_{{||}}},$ которые разделяют различные фазы суспензии в раскрученном состоянии, характеризуя границы переходов между фазами I и III, II и III, III и IV, так же следуют из формул (8), (9) и (12). Разные типы угловых зависимостей разделяет значение $\gamma = 1.$ Если $\gamma < 1,$ то при увеличении энергии сцепления система проходит фазы IV–III–II, а при $\gamma > 1$ последовательность фаз: IV–III–I. Таким образом, ключевым параметром, определяющим последовательность ориентационных фаз в раскрученном состоянии суспензии, является параметр анизотропии диамагнитной восприимчивости $\gamma ,$ который отвечает за тип механизма воздействия поля на композитную жидкокристаллическую систему.

ЗАКЛЮЧЕНИЕ

Рассмотрены ориентационные переходы в раскрученной фазе хиральной ЖК-суспензии диамагнитных частиц в магнитном поле. Определены области значений магнитного поля и параметров анизотропии и сцепления, в которых реализуются однородные гомеотропная, угловая и планарная фазы. Найдены критические поля переходов между этими фазами. Построены зависимости углов директоров подсистем от материальных параметров суспензии σ и γ, а также полевые зависимости углов.

Работа выполнена при финансовой поддержке РФФИ (проект № 19-02-00231) и Минобрнауки России (проект № FSNF-2020-0008).