Известия РАН. Серия физическая, 2022, T. 86, № 2, стр. 199-204

ВВЕДЕНИЕ

Для систем с расслоением (это может быть бинарный раствор или однокомпонентная система в замкнутом объеме ниже критической точки) теория распада однородного состояния при переходе в двухфазную область развита хорошо: если система оказывается за спинодалью, применяется теория спинодального распада, в противном случае – теория зародышеобразования (для обзора см. [1, 2]). Обратная ситуация – растворение второй фазы при переходе в однофазную область – изучена меньше. Это связано с тем, что, в отличие от первого случая, не существует универсального начального состояния: можно указать множество начальных конфигураций неравновесной второй фазы (отличающихся, например, морфологией и дисперсностью), для которых динамика растворения и границы метастабильной устойчивости будут разными. Вместе с тем изучение динамики распада второй фазы представляется актуальным. Особенно это касается практически важных металлических эвтектических систем, для которых микрогетерогенность после нагрева в жидкую однофазную область может сохраняться длительное время [3].

Таким образом, мы рассматриваем систему с расслоением вблизи границы двухфазной области на диаграмме температура – концентрация, с внешней стороны. Ситуация схематически представлена на рис. 1 (нижний фрагмент), точка S соответствует равновесному состоянию системы, которое является однофазным. Предполагается, что система попала в эту точку из двухфазной области путем быстрого изменения температуры, так что в ней может присутствовать некоторое количество неравновесной второй фазы, которую мы полагаем мелкодисперсной, так что ее объемная доля описывается полевой переменной $Z(\vec {r}).$ При этом имеется в виду, что размер “физической точки” $\vec {r}$ превышает дисперсность фазы. Вблизи двухфазной области зависимость удельного термодинамического потенциала от концентрации F(c) при заданной температуре Т имеет вид, представленный на верхнем фрагменте. Глобальный минимум соответствует точке S на фазовой диаграмме, а границы двухфазной области определяются c помощью общей касательной. Как упомянуто выше, начальное двухфазное состояние, релаксация которого к однородному и гомогенному, собственно, и рассматривается, может иметь весьма разнообразные первоначальные реализации, отличающиеся морфологией и дисперсностью. Мы полагаем, что можно выделить тип начальных условий, а именно – удовлетворяющие уже упомянутому допущению о том, что неравновесная фаза является мелкодисперсной, а ее объемная доля описывается полевой переменной $Z(\vec {r}),$ – которые соответствуют некоторому обширному классу систем, в частности – эвтектическим сплавам. Обсуждение этого вопроса приведено в заключении.

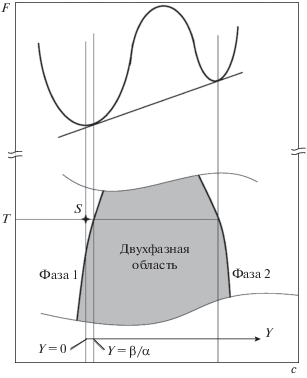
Таким образом, система описывается двумя полями – уже упомянутым $Z(\vec {r}),$ а также полем локальных отклонений концентрации $Y(\vec {r})$ в объемной матрице первой фазы от равновесной, которая соответствует точке $S$ на рис. 1 и совпадает со средней по системе, поскольку равновесное состояние – однофазное. Для исследования динамики нам потребуется удельный неравновесный термодинамический потенциал $F\left\{ {Y(\vec {r}),Z(\vec {r})} \right\}$ как функционал этих полей, после чего динамические уравнения запишутся в стандартном виде (см., например, [4]):

Здесь γ, g – феноменологические коэффициенты, a $\theta (\vec {r},t)$ – случайная сила, моделирующая взаимодействие с термостатом. Оператор Лапласа в правой части первого уравнения возникает потому, что поле $Y(\vec {r})$ при отсутствии второй фазы подчиняется закону сохранения

В общем виде функционал $F\left\{ {Y(\vec {r}),Z(\vec {r})} \right\}$ записывается в виде

где N – число частиц в системе, а плотность потенциала

Первые два слагаемых – стандартное квадратичное приближение для флуктуаций концентрации, остальные представляют собой вклад от второй фазы. При этом при малом ее количестве функция f(Z) ведет себя как

Вид двух последних членов неравновесной плотности потенциала (4,5) вполне очевиден: если локальная флуктуация концентрации $Y(\vec {r})$ превышает β/α, то локально мы попадаем в двухфазную область (см. рис. 1), и локально равновесное количество второй фазы оказывается, благодаря асимптотике (5), пропорционально величине этого превышения с коэффициентом ε/α. Таким образом, выбор α, β и ε позволяет моделировать расстояние до двухфазной области, разность концентраций и потенциалов между фазами. Заметим, что f(Z) быстро возрастает с ростом Z, поскольку для заметного увеличения количества второй фазы требуется большая флуктуация Y, а если, как мы полагаем, такие флуктуации малы, то вторая фаза получится сильно обедненной вторым компонентом, что резко увеличивает потенциал. Для дальнейших рассуждений конкретный вид f(Z) нам не потребуется.

Случайная сила в (1) моделирует взаимодействие с термостатом, ее свойства обычно определяются на основе флуктуационно – диссипационной теоремы. В нашем случае это означает, что ее коррелятор

Таким образом, для описания концентрационной динамики нам нужно исследовать систему (1) при различных начальных условиях и возможных приближениях. В частности, нас интересует случай, когда в некоторой области имеется ненулевая начальная доля второй фазы. Заметим, что система (1) соответствует модели H критической диффузии [5] в системе с ловушками, роль которых выполняют частицы второй фазы. С другой стороны, она вполне идентична динамике химической реакции с превращением Z ⇔ Y, происходящей в изотермических условиях. При исследовании такой динамики принято [6] сначала исследовать однородные (без диффузии) решения, а затем – возможные пространственные конфигурации. Первый шаг представлен ниже.

РЕШЕНИЕ С ОГРАНИЧЕННОЙ ДИФФУЗИЕЙ

В явном виде вариационные производные, входящие в систему (1), есть

так что имеем:

Если пренебречь диффузией (γ → 0), то система примет вид

где точкой обозначено дифференцирование по переменной gt = τ. Система (9) позволяет записать замкнутое уравнение на Z:

которое имеет очевидный первый интеграл

Уравнение (10) идентично задаче об одномерном движении по координате Z в “потенциале”

для которой возможные Z(τ) обсуждаются, например, в [7]. В зависимости от параметров модели и вида функции f(Z) “потенциал” (12) может выглядеть по-разному (рис. 2).

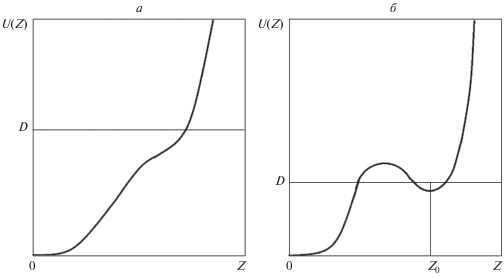
В первом случае (рис. 2а) некоторое начальное количество второй фазы быстро уменьшается до нуля. Во втором случае (рис. 2б) возможно нетривиальное поведение количества второй фазы – колебания вблизи минимума при Z = Z₀ c некоторой частотой и амплитудой, задаваемой постоянной интегрирования D. Если амплитуда мала, то их частота

в соответствии с уравнением

Отметим, что релаксация переменной Z до нуля имеет однократный характер: однажды достигнув нуля, Z снова вырасти не cможет, даже если локальная флуктуация концентрации превысит уровень β/α: для этого необходимо возникновение зародыша, и плотность потенциала (4) в этом случае не является адекватной.

Ясно, что колебания вблизи минимума – нетривиальное поведение, и нужно выяснить, устойчиво ли оно по отношению к диффузии.

УСТОЙЧИВОСТЬ ПО ОТНОШЕНИЮ К ДИФФУЗИИ

При γ ≠ 0 появятся взаимодействие с термостатом и диффузия. Из-за взаимодействия с термостатом колебания (14) вблизи Z₀ станут затухающими [4]. Возникает вопрос – существуют ли такие начальные конфигурации системы, для которых “облако” частиц второй фазы будет устойчивым по отношению к его диффузионному растворению? Рассмотрим ситуацию, когда такое облако частиц второй фазы занимает объемную область с гладкой границей.

Справа на рис. 3а изображена область (возникшая в качестве начального возмущения при приготовлении системы, на рисунке, затемнена) с количеством второй фазы Z₀ и с повышенным содержанием второго компонента Y₀ = $\frac{1}{\alpha }\left( {\beta + \frac{{f{\kern 1pt} '({{Z}_{0}})}}{{{{Z}_{0}}}}} \right).$ Слева – область, обедненная вторым компонентом, в которой Z = 0, Y = –Y₁. Мы рассматриваем почти плоскую границу между этими областями (промежуточная область на рис. 3а). Постоянные, не зависящие от координаты концентрации Y₁, Y₀ дают стационарное решение (8) слева и справа. В промежуточной области стационарное решение соответствует краевой задаче:

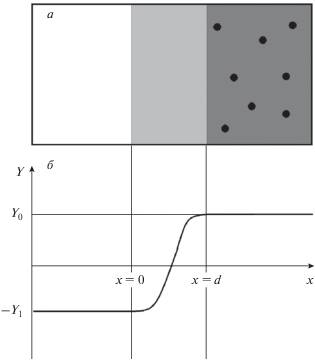
решение которой есть:

Вопрос теперь состоит в том, возможна ли гладкая сшивка (16) с состоянием справа, в котором Y = Y₀. Ответ очевиден: она возможна, поскольку имеется два свободных параметра – степень обеднения Y₁ и толщина переходной области d, чего достаточно для согласования как самой функции, так и ее производной. Степень обеднения зависит от начальных условий: чем больше начальная область с повышенным содержанием второго компонента, тем больше, соответственно, Y₁. Для того, чтобы стационарное решение осуществилось, необходимо, чтобы

В этом случае, по мере растворения, эти концентрации выровняются, так что будет

Ширина переходного слоя установится автоматически на уровне

который, в соответствии с принципом минимума производства энтропии, соответствует минимальной (в данном случае нулевой) скорости диффузии и гладкой сшивке решений во всех трех областях (рис. 3б). Устойчивость плоской границы означает также устойчивость образований с гладкой (локально плоской) границей.

Таким образом, вблизи бинодали со стороны гомогенности могут существовать области с повышенным содержанием второго компонента и вкраплениями второй фазы, количество которой определяется минимумом функции (12), устойчивые по отношению к диффузионному растворению – долгоживущие гетерофазные неоднородности. Для их релаксации требуется диффузия самих частиц второй фазы, что является медленным процессом.

ЗАКЛЮЧЕНИЕ

Исследована динамика рассмотренной системы (1.8) по упрощенной схеме. Вообще говоря, более общий путь [8] подразумевает, что если имеется стохастическая динамика некоторой системы, описываемая вектором переменных $V(\vec {r},t),$ выведенная из принципа минимума функционала F:

где $\hat {\Gamma }$ – некоторый линейный оператор, а θ – белый шум:

то для такой динамики можно записать уравнение Фоккера–Планка для функции распределения по конфигурациям полей $P\left\{ {\vec {V}(\vec {r},t)} \right\}{\text{:}}$

Стандартным стационарным решением этого уравнения является распределение Гиббса:

Обнаруженные нами долгоживущие гетерофазные неоднородности говорят о том, что это не единственное стационарное решение.

Еще раз перечислим приближения, использованные нами при обсуждении долгоживущей гетерофазной неоднородности:

1) система находится вдали от критической точки и от спинодали;

2) вторая фаза является мелкодисперсной, ее доля мала и может описываться полевой переменной;

3) стартовые неоднородности довольно обширны, что создает достаточную степень обеднения в остальном материале, и обладают гладкой границей, напоминая по форме кучевое облако;

4) функция f(Z) обеспечивает наличие минимума у потенциала (12)

Второе приближение заслуживает дополнительного комментария. При росте или растворении малых частиц сильно меняется кривизна их поверхности, что, на первый взгляд, должно приводить к сильному изменению их внутреннего давления и, следовательно, термодинамического потенциала. Этого, однако, не происходит, поскольку для малых частиц поверхностное натяжение пропорционально их размеру [9], так что давление остается неизменным.

Эти приближения могут реализоваться в системах с эвтектическим (или эвтектоидным) равновесием. Рассмотрим, например, ситуацию, представленную на рис. 4. Пусть система с концентрацией c₀ быстро нагревается от T₁ до T₂, соответственно вертикальной стрелке. В этом случае можно утверждать, что в начальном состоянии в системе имеется большое количество фазы 2, равное a/(a + b), в соответствии с правилом рычага.

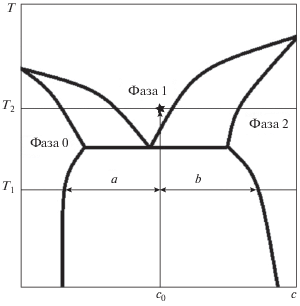
Кроме того, эта фаза мелкодисперсна, что является общим свойством эвтектических систем (см., например, [10]). При быстром нагреве эта ситуация некоторое время сохранится и в жидкости, так что ситуация вполне соответствует нашим приближениям. Таким образом, “доплавление” в эвтектической системе может быть длительным, с существованием больших “облаков” мелкодисперсной второй фазы, разрушение которых является гидродинамическим процессом. Такие процессы, в отличие от диффузии и самодиффузии (см. например [11]) являются медленными и не учитываются нашей моделью. Поведение, подпадающее под этот сценарий, описано в работах, в которых измерялись температурные и временные зависимости различных физических свойств расплавов эвтектических систем – в качестве обзора (см [3, 12]). В частности, наблюдалось длительное существование неравновесных состояний, которые разрушались только при нагреве до некоторых пороговых температур. Кроме того, отмечались затухающие осцилляции физических свойств со временем, что соответствует уравнению (14) с малым затуханием. Можно также отметить работу [13], в которой наблюдалось немонотонное изменение состава поверхности околоэвтектического металлического расплава, что можно связать с гидродинамическим выходом на поверхность гетерогенного “облака”.

Исследование выполнено при поддержке Российского научного фонда (проект № 21-13-00202).