Известия РАН. Серия физическая, 2022, T. 86, № 3, стр. 316-321

ВВЕДЕНИЕ

Вопрос о механизмах формировании тонкого токового слоя (далее ТТС) в ближнем хвосте магнитосферы Земли на предварительной фазе суббури и его последующего распада во время взрывной фазы является одной из важных и до конца не решенных проблем физики магнитосферной суббури. Экспериментальные данные указывают на часто наблюдаемые различия между суббурями, происходящими в возмущенных условиях, и изолированными суббурями. Это отличие давно связывают с ионами кислорода ионосферного происхождения [1, 2]. Основанием для такого предположения является наблюдаемое на предварительной фазе суббури в возмущенных условиях повышение относительной доли ионов кислорода в плазменном слое от значений порядка 1–2% до значений свыше 50% [3, 4], а также неоднократное обнаружение в околоземной магнитосфере потоков ионов кислорода, направленных от Земли в хвост [5–10]. Кроме того, в работе [11] было обнаружено присутствие токонесущих ионов кислорода при пересечении токового слоя (ТС) ближнего хвоста аппаратами миссии CLUSTER.

До недавнего времени известные экспериментальные данные не позволяли достаточно точно оценить характерные параметры встречных потоков ионов кислорода в плазменном слое, знание которых необходимо для детального численного моделирования ТТС. В недавней работе [12] этот пробел был восполнен. В результате анализа данных миссии THEMIS было показано, что в плазменном слое наблюдаются потоки ионов кислорода O⁺ ионосферного происхождения, направленные в хвост вдоль силовых линий магнитного поля, которые достигают токовый слой хвоста в интервале расстояний примерно $20{{R}_{E}} \leqslant - x \leqslant 40{{R}_{E}},$ а также были получены следующие оценки параметров этих потоков. Характерное значение температуры ионов кислорода составляет сотни эВ: ${{T}_{{\text{O}}}} \sim 0.1 - 0.9$ кэВ, и меньше температуры электронов ${{T}_{e}}$, которая имеет характерное значение в 1 кэВ, а температура протонов обычно лежит в диапазоне ${{T}_{p}} = 4 - 10$ кэВ. Величина гидродинамической скорости потоков ионов кислорода вдоль силовых линий ${{V}_{{D{\text{O}}}}}$ имеет типичные значения примерно 100‒250 км/с. Отсюда следует, что гирорадиусы R_cO ионов O⁺ и протонов R_cp оказываются сравнимыми: $\frac{{{{R}_{{c{\text{O}}}}}}}{{{{R}_{{cp}}}}}$ = $\sqrt {\frac{{\left( {{{m}_{{\text{O}}}}{{T}_{{\text{O}}}}} \right)}}{{\left( {{{m}_{p}}{{T}_{p}}} \right)}}} $ ≈ $4\sqrt {\frac{{{{T}_{{\text{O}}}}}}{{{{T}_{p}}}}} \sim 0.4 - 1.$

Отметим, что для температур из указанных диапазонов тепловые скорости ионов кислорода ${{V}_{{T{\text{O}}}}} = \sqrt {{{e{{T}_{{\text{O}}}}} \mathord{\left/ {\vphantom {{e{{T}_{{\text{O}}}}} {{{m}_{{\text{O}}}}}}} \right. \kern-0em} {{{m}_{{\text{O}}}}}}} $ и протонов ${{V}_{{Tp}}} = \sqrt {{{e{{T}_{p}}} \mathord{\left/ {\vphantom {{e{{T}_{p}}} {{{m}_{p}}}}} \right. \kern-0em} {{{m}_{p}}}}} $ лежат в пределах примерно ${{V}_{{T{\text{O}}}}} \approx 25{\kern 1pt} - {\kern 1pt} 75$ км/с и ${{V}_{{Tp}}} \approx 619{\kern 1pt} - {\kern 1pt} 1000$ км/с, т.е. для ионов кислорода значения безразмерного параметра потока ${{\delta }_{{\text{O}}}} = {{{{V}_{{D{\text{O}}}}}} \mathord{\left/ {\vphantom {{{{V}_{{D{\text{O}}}}}} {{{V}_{{T{\text{O}}}}}}}} \right. \kern-0em} {{{V}_{{T{\text{O}}}}}}}$ лежат в диапазоне примерно ${{\delta }_{{\text{O}}}} \sim 3{\kern 1pt} - {\kern 1pt} 10.$

Таким образом, для возмущенных условий на предварительной фазе суббури вполне возможной представляется ситуация, когда вблизи нейтрального слоя ближнего хвоста имеются встречные потоки ионов O⁺ с температурой ${{T}_{{\text{O}}}} \sim 0.1{\kern 1pt} - {\kern 1pt} 0.4$ кэВ и гидродинамической скоростью вдоль линий магнитного поля ${{V}_{{D{\text{O}}}}} \sim 200{\kern 1pt} - {\kern 1pt} 250$ км/с, а протоны либо являются фоном, либо имеют небольшое значение параметра потока ${{\delta }_{p}} = {{{{V}_{{Dp}}}} \mathord{\left/ {\vphantom {{{{V}_{{Dp}}}} {{\kern 1pt} {{V}_{{Tp}}}}}} \right. \kern-0em} {{\kern 1pt} {{V}_{{Tp}}}}} < 1.$

В этой работе с помощью численной модели стационарного ТТС, которая детально описана в [13], получены его конфигурации, образованные встречными потоками ионов кислорода для случая, когда потоками протонов можно пренебречь, то есть протоны являются фоновой компонентой. Параметры ТС в полученных конфигурациях согласуются с известными экспериментальными данными. Полученные конфигурации ТТС на ионах кислорода имеют ряд отличий от ТТС, образованных потоками протонов, которые было бы интересно проверить на данных спутниковых миссий MMS, THEMIS и CLUSTER.

Отметим, что эта работа является продолжением и уточнением работы [14], в которой при помощи приближенной аналитической модели были получены стационарные конфигурации ТТС с учетом потоков ионов кислорода для следующего набора вариантов значений безразмерных параметров вне слоя ${{{{n}_{{\text{O}}}}} \mathord{\left/ {\vphantom {{{{n}_{{\text{O}}}}} {{{n}_{p}}}}} \right. \kern-0em} {{{n}_{p}}}}$ = $0,\,\,0.1,\,\,0.25,\,\,0.5,1$ и ${{{{T}_{{\text{O}}}}} \mathord{\left/ {\vphantom {{{{T}_{{\text{O}}}}} {{{T}_{p}}}}} \right. \kern-0em} {{{T}_{p}}}}$ = $0,\,\,0.1,\,\,0.25,\,\,0.5,\,\,1.$ В ней впервые было показано, что при наличии потоков ионов кислорода возможно значительное расширение токового слоя, но были получены только безразмерные профили концентрации ионов кислорода и протонов, что затрудняет сравнение с данными измерений, а также не рассматривался важный вариант, когда имеются только потоки ионов кислорода, а протоны являются фоном. Кроме того, в рассмотренных вариантах продольная гидродинамическая скорость потоков ионов кислорода считалась равной скорости потоков протонов: ${{V}_{{D{\text{O}}}}} = {{V}_{{Dp}}} \sim {{V}_{{Tp}}}$ ≈ $600{\kern 1pt} - {\kern 1pt} 1000$ км/с, что является существенно завышенным значением, поскольку из анализа последних экспериментальных данных [12] получена оценка ${{V}_{{D{\text{O}}}}} \leqslant 250$ км/с.

МЕХАНИЗМ ВЫТЯГИВАНИЯ ИОНОВ ИЗ ИОНОСФЕРЫ

В возмущенных условиях в высокоширотных областях F-слоя ионосферы Земли усиливается ионизация и происходит дополнительный нагрев заряженных компонент, что приводит к повышению давления электронов. В результате, по сравнению со спокойными условиями, в этих областях ионосферы и в примыкающей к ним области ближней магнитосферы усиливается продольное электрическое поле. Это поле определяется из условия продольного силового равновесия электронов, которое в случае пренебрежения столкновениями электронов и учета их замагниченности принимает вид [15]:

где $\vec {B}{\kern 1pt} \left( {\vec {x},t} \right)$ и $\vec {E}\left( {\vec {x},t} \right)$ ‒ векторы индукции магнитного поля и напряженности электрического поля, ${{n}_{e}}\left( {\vec {x},t} \right)$ – концентрация электронов, через $\left( {\vec {u} \cdot \vec {\nu }} \right)$ обозначено скалярное произведение векторов, ${{p}_{{e\parallel }}}{\kern 1pt} \left( {\vec {x},t} \right)$ и ${{p}_{{e \bot }}}\left( {\vec {x},t} \right)$ – продольное и поперечное давление электронов по отношению к направлению магнитного поля. В случае изотропии давления электронов это уравнение примет вид

Как известно, давление электронов падает по мере удаления от Земли, поэтому его градиент $\nabla {{p}_{e}}$ направлен к Земле, а определяемое формулой (2) продольное электрическое поле в высокоширотной ионосфере направлено от Земли. Такое поле вытягивает ионы кислорода из F-слоя высокоширотной ионосферы в плазменный слой и ускоряет их.

ЧИСЛЕННАЯ МОДЕЛЬ СТАЦИОНАРНОГО ТТС

В рассматриваемой модели ТТС с размерностью 1D3V магнитное поле имеет заданную постоянную нормальную компоненту ${{B}_{z}} \equiv Const$ и самосогласованные компоненты ${{B}_{x}}\left( z \right)$ и ${{B}_{y}}\left( z \right),$ а электрическое поле имеет одну самосогласованную компоненту ${{E}_{z}}\left( z \right){\text{:}}$

где через ${{\varphi }}{\kern 1pt} \left( {z} \right)$ обозначен скалярный потенциал, а через ${{\vec {e}}_{x}},$ ${{\vec {e}}_{y}}$ и ${{\vec {e}}_{z}}$ обозначены векторы декартова базиса системы координат. Вне области моделирования $\left\{ {\left| z \right| < L} \right\}$ магнитное поле считается постоянным, а электрическое нулевым:

Здесь и далее верхние индексы (+) и (–) обозначают, соответственно, значения функции на верхней и нижней границах ТС. Удобно выбрать ось X вдоль вектора изменения магнитного поля при переходе через слой:

Тогда компонента ${{B}_{y}}\left( z \right)$ будет сдвиговой (шировой), т.е. ${{B}_{y}}\left( z \right)$ может изменятся внутри слоя, но не меняется при переходе через слой, а компонента ${{B}_{x}}\left( z \right)$ будет тангенциальной: ${{B}_{y}}\left( { - L} \right) = {{B}_{y}}\left( L \right),$ $\Delta B = {{B}_{x}}\left( L \right)$ – ${{B}_{x}}\left( { - L} \right).$

Слой поддерживается встречными потоками ионов вдоль силовых линий магнитного поля. Функция распределения $f_{{{\alpha }}}^{{( \pm )}}\left( {z,\vec {v}} \right)$ каждого сорта ионов в падающих потоках плазмы на границе области расчетов имеет вид распределения Максвелла с гидродинамической скоростью $\vec {U}_{{{\alpha }}}^{{( \pm )}} = - \frac{{z{{{\vec {B}}}^{{( \pm )}}}V_{{D{{\alpha }}}}^{{( \pm )}}}}{{\left| z \right|\left| {{{{\vec {B}}}^{{( \pm )}}}} \right|}},$ которая направлена вдоль силовых линий магнитного поля в сторону слоя и имеет величину $V_{{D{{\alpha }}}}^{{( \pm )}}$ (свою для каждого сорта ионов):

Здесь $n_{{{\alpha }}}^{{( \pm )}}$ – концентрация, $T_{{{\alpha }}}^{{( \pm )}}$ – температура в эВ, $V_{{T{{\alpha }}}}^{{( \pm )}} = \sqrt {{{eT_{{{\alpha }}}^{{( \pm )}}} \mathord{\left/ {\vphantom {{eT_{{{\alpha }}}^{{( \pm )}}} {{{m}_{{{\alpha }}}}}}} \right. \kern-0em} {{{m}_{{{\alpha }}}}}}} $ – тепловая скорость в этих потоках.

В модели ионные компоненты описываются стационарными уравнениями Власова, которые решаются численно. Замагниченные электроны описываются стационарным уравнением Власова в дрейфовом приближении (см. [13, 15 , 16–20]), а их плотность тока в соответствии с дрейфовой теорией описывается формулой

где $\vec {b}\left( {\vec {x},t} \right) = {{\vec {B}} \mathord{\left/ {\vphantom {{\vec {B}} B}} \right. \kern-0em} B}$ – единичный вектор вдоль магнитного поля. Электрическое поле определяется из условия продольного силового равновесия электронов (2), которое в рассматриваемом случае принимает вид

Продольный ток электронов в квазинейтральной плазме с замагниченными электронами определяется из условия ${\text{div}}\vec {j} = 0,$ которое в рассматриваемой задаче с полями вида (3) равносильно отсутствию z-компоненты у плотности полного тока: ${{j}_{z}}{\kern 1pt} \left( z \right) \equiv 0.$ Плотность полного тока определяется формулой

где плотность тока ионов ${{\vec {j}}_{{i{\kern 1pt} }}}\left( z \right)$ рассчитывается численно. Подстановка равенства ${{j}_{z}}\left( z \right) \equiv 0$ в z‑компоненту уравнения (9) позволяет выразить продольную компоненту плотности тока электронов через остальные слагаемые:

что дает следующие формулы для плотности тока электронов:

Таким образом, уравнение Ампера ${\text{rot}}\vec {B} = {{{{\mu }}}_{0}}\vec {j}$ в модели сводится к системе из двух обыкновенных дифференциальных уравнений 1-го порядка относительно самосогласованных компонент магнитного поля:

в которой правая часть может зависеть от ${{B}_{x}}\left( z \right)$ и ${{B}_{y}}\left( z \right),$ а также от их производных.

Подстановка выражения электрического поля по формуле (8) во второе слагаемое в правой части формулы (7), с учетом вида полей (3), позволяет представить плотность тока электронов в форме

Из этой формулы вытекает, что в случае изотропного давления электронов ${{p}_{{e\parallel }}} = {{p}_{{e \bot }}} = {{p}_{e}}$ они могут давать только нейтрализующий продольный ток, который в рассматриваемом ниже симметричном случае отсутствует.

В [13] показано, что для описывающего электроны пространственно 1-мерного стационарного уравнения Власова в дрейфовом приближении с полями вида (3) функция распределения Максвелла–Больцмана является точным решением при отсутствии шировой компоненты магнитного поля (т.е. при ${{B}_{y}}\left( z \right) \equiv 0$), и является приближенным решением, если ${{B}_{y}}\left( z \right) \ne 0.$ Это распределение удобно представить в виде

где постоянные ${{B}_{0}} = B\left( {{{z}_{0}}} \right),$ ${{n}_{0}} = n\left( {{{z}_{0}}} \right),$ ${{{{\gamma }}}_{0}} = {{\gamma }}\left( {{{z}_{0}}} \right)$ = = $\frac{{{{p}_{{e\parallel }}}\left( {{{z}_{0}}} \right) - {{p}_{{e \bot }}}\left( {{{z}_{0}}} \right)}}{{{{p}_{{e \bot }}}\left( {{{z}_{0}}} \right)}},$ являются значениями соответствующих функций в некоторой точке слоя ${{z}_{0}},$ т.е. ${{{{\gamma }}}_{0}}$ – безразмерный параметр анизотропии (${{{{\gamma }}}_{0}} = 0$ в случае изотропии), ${{T}_{{e\parallel }}}$ – продольная электронная температура в эВ, а ${{V}_{{Te\parallel }}} = \sqrt {\frac{{e{{T}_{{e\parallel }}}}}{{{{m}_{e}}}}} $ – соответствующая тепловая скорость электронов. Функция распределения (14) дает следующие формулы, которые связывают концентрацию электронов ${{n}_{e}}\left( z \right) = n\left( z \right)$ со скалярным потенциалом и магнитным полем:

а также дает следующие формулы для давлений и температур электронов:

подстановка которых в формулу (7) приводит к следующим выражениям для компонент плотности тока

Из формул (16) следует, что если давление электронов изотропно вне токового слоя $\left( {{{{{\gamma }}}_{0}} = 0} \right),$ то оно будет также изотропно и внутри слоя, а температура электронов будет постоянной: ${{T}_{e}} \equiv {\text{const}}.$ Тогда формулы (14) и (15) примут следующий вид:

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

В результате расчетов были получены стационарные симметричные плоские конфигурации ТТС, образованные либо потоками протонов, либо потоками ионов кислорода. В этом случае магнитное поле имеет две компоненты, и выполнены условия симметрии ТС:

Давление электронов считалось изотропным, т.е. их ток, согласно (18), равен нулю.

На рис. 1 показаны две конфигурации, образованные потоками ионов кислорода с температурой ${{T}_{{\text{O}}}} = 0.4$ кэВ (красная линяя), и ${{T}_{{\text{O}}}} = 0.2$ кэВ (синяя линяя), для которых параметр потока равен ${{\delta }_{{\text{O}}}} = {{{{V}_{{D{\text{O}}}}}} \mathord{\left/ {\vphantom {{{{V}_{{D{\text{O}}}}}} {{{V}_{{T{\text{O}}}}}}}} \right. \kern-0em} {{{V}_{{T{\text{O}}}}}}} = 5,$ что соответствует значениям продольной скорости ${{V}_{{D{\text{O}}}}} \approx 250$ км/с и ${{V}_{{D{\text{O}}}}} \approx 175$ км/с. Также для сравнения черной линией показана типичная конфигурация ТТС, образованного потоками протонов с температурой ${{T}_{p}} = 4$ кэВ и с параметром потока ${{\delta }_{p}} = 1.5,$ что соответствует продольной скорости ${{V}_{{Dp}}} \approx 930$ км/с. Для всех случаев использовались значения нормальной компоненты магнитного поля ${{B}_{z}} = 2.5$ нТл и его тангенциальной компоненты вне слоя ${{B}_{{x0}}} = 20$ нТл.

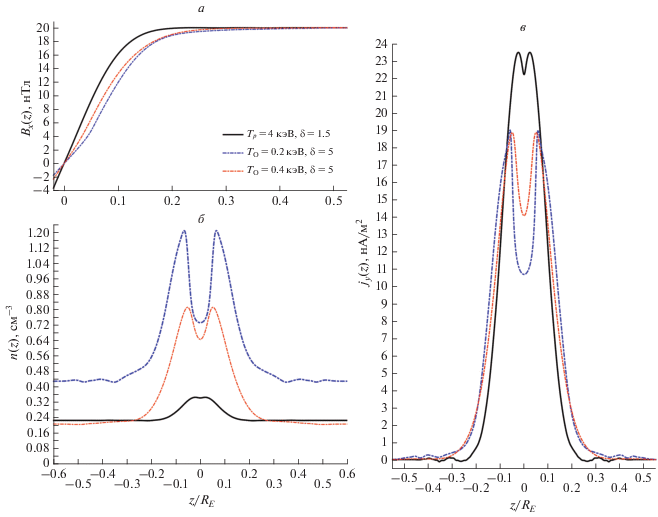
Из рис. 1 видно, что ТТС, образованный потоками ионов кислорода, примерно в 1.5 раза шире по сравнению с ТТС, образованным потоками протонов, а провал в центре слоя (расщепление или бифуркация) в профилях плотности тока и концентрации на порядок глубже. Отметим, что для потоков ионов кислорода с понижением температуры в 2 раза ширина ТТС практически не изменилась, но провал в профиле плотности тока в центре ТС стал примерно в 1.7 раза глубже, а концентрация на краях ТТС изменилась в соответствии с оценкой ${{\left. {{{T}_{{{\text{O}}1}}}{{n}_{{\text{O}}}}\left( L \right)} \right|}_{{{{T}_{{{\text{O}}1}}}}}}$ ≈ ${{T}_{{{\text{O}}2}}}{{\left. {{{n}_{{\text{O}}}}\left( L \right)} \right|}_{{{{T}_{{{\text{O}}2}}}}}}.$

Также отметим, что вариант ТТС на ионах кислорода с температурой ${{T}_{{\text{O}}}} = 0.2$ кэВ в центре имеет достаточно большую максимальную концентрацию ${{n}_{{max}}} \approx 1.2$ см^–3, что превышает характерные наблюдаемые значения $n \leqslant 1$ см^–3. Из этого можно сделать вывод, что в случае более холодных потоков ионов кислорода для получения в модели приемлемой концентрации ${{n}_{{max}}} \leqslant 1$ см^–3 их продольная гидродинамическая скорость должна быть примерно ${{V}_{{D{\text{O}}}}} \approx 250$ км/с, что соответствует безразмерному параметру потока ${{\delta }_{{\text{O}}}} \approx 7.$

ЗАКЛЮЧЕНИЕ

Таким образом, из результатов моделирования можно сделать вывод, что в возмущенных условиях в ближнем хвосте магнитосферы ТС может быть образован потоками ионов кислорода из ионосферы при пренебрежительно малых потоках протонов. Моделирование выявило ряд отличий такого ТТС от образованного потоками протонов. Эти отличия могут существенно влиять на устойчивость ТТС.

Для дальнейшего изучения вопроса о формировании ТС в ближнем хвосте в возмущенных условиях необходим целенаправленный анализ данных спутниковых миссий MMS, THEMIS и CLUSTER, чтобы набрать статистику пересечения ими указанного ТС, и проверить наличие в этих данных потоков ионов кислорода.