Известия РАН. Серия физическая, 2022, T. 86, № 4, стр. 601-608
Восстановление спектров промышленных ускорителей электронов по глубинным дозовым распределениям
У. А. Близнюк 1, 2, *, П. Ю. Борщеговская 1, 2, В. С. Ипатова 2, А. Д. Никитченко 1, Ф. Р. Студеникин 1, 2, А. П. Черняев 1, 2
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный университет имени М.В. Ломоносова”, Физический факультет
Москва, Россия
2 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный университет имени М.В. Ломоносова”,
Научно-исследовательский институт ядерной физики имени Д.В. Скобельцына
Москва, Россия
* E-mail: uabliznyuk@gmail.com
Поступила в редакцию 15.11.2021
После доработки 06.12.2021
Принята к публикации 22.12.2021
- EDN: MBWEVW
- DOI: 10.31857/S0367676522040068
Аннотация
Проведено восстановление спектров пучков электронов от промышленного ускорителя по глубинным дозовым распределениям в алюминии с использованием различных методов выбора параметра регуляризации Тихонова. Оценено влияние погрешностей измерения глубинных дозовых распределений на восстановленные спектры и соответствующие этим реконструированным спектрам дозовые распределения.
ВВЕДЕНИЕ
Глобальный темп развития радиационных технологий (РТ) связан с высокой эффективностью, экологической безопасностью и повышенной востребованностью во многих областях науки и техники. На сегодняшний день в мире наблюдается неуклонный рост количества медицинских и промышленных центров, работающих на базах ускорительных комплексов с целью решения целого ряда научно-прикладных задач [1, 2]. Среди современных радиационных установок значительное положение занимают ускорители электронов [3]. Необходимым условием успешного применения РТ является наличие информации о пространственном распределении поглощенной дозы в облучаемом объекте, которое определяется как свойствами облучаемого объекта (геометрией, элементным составом, плотностью), так и свойствами облучателя, в первую очередь энергетическим спектром пучка [4, 5].
На сегодняшний день существуют следующие подходы к определению энергетических спектров ускорителей: (а) моделирование источника излучения методом Монте-Карло [5], (б) прямое измерение энергетического спектра с использованием специального оборудования [6], (в) косвенный метод, основанный на реконструкции спектрального состава пучка по экспериментально измеренным данным [7, 8]. Метод (а) является наиболее точным при условии учета всех технических характеристик ускорителя и схемы облучения, что не всегда является возможным [9]. Метод (б) предполагает использование редкого и дорогостоящего оборудования или наличия подобных систем в составе ускорителя, что также приводит к повышению его стоимости. В свою очередь, метод (в) является наиболее доступным, хотя и уступает в точности методам (а) и (б) [10].
Косвенный метод восстановления энергетического спектра электронов в пучке связан с решением обратной задачи, которая в общем виде может быть сформулирована следующим образом:
где $D\left( x \right)$ – распределение некоторой характеристики11 (заряд, доза, флюенс, плотность потока и пр.) исследуемого пучка по глубине x; $d\left( {x,E} \right)$ – глубинное распределение той же характеристики для моноэнергетического пучка с энергией E; $f\left( E \right)$ – энергетический спектр.Значения D(x) известны лишь в конечном наборе точек ${{x}_{i}},$ а глубинные распределения для конечного числа пучков поэтому, уравнение (1) можно представить в матричном виде:
где ${{d}_{{ji}}}$ – значение поглощенной дозы в точке с координатой ${{x}_{i}},$ создаваемое пучком электронов, с энергетическим спектром, описываемым некоторой известной базисной функцией ${{I}_{j}}\left( E \right).$Как правило, это или моноэнергетические пучки, или пучки, имеющие равномерное распределение в интервале $\left( {{{E}_{j}} - {{\Delta E} \mathord{\left/ {\vphantom {{\Delta E} 2}} \right. \kern-0em} 2},{{E}_{j}} + {{\Delta E} \mathord{\left/ {\vphantom {{\Delta E} 2}} \right. \kern-0em} 2}} \right).$ Хотя могут быть использованы и другие виды распределений ${{I}_{j}}\left( E \right).$ В данной работе используются равномерные базисные функции с различными значениями $\Delta E$ и ${{E}_{j}}.$ Соответственно ${{D}_{i}} \equiv D\left( {{{x}_{i}}} \right) = \sum\nolimits_j {{{f}_{j}}{{d}_{{ji}}}} $ – значение поглощенной дозы в точке с координатой ${{x}_{i}},$ создаваемое пучком с некоторым распределением, которое разложено по базисным функциям с весами ${{f}_{j}}.$
Истинное значение D на практике неизвестно, имеются только результаты измерений ${{D}_{{exp}}}{\text{,}}$ которые известны с некоторой погрешностью ${{\delta }}{{D}_{{exp}}}.$ Эта погрешность является случайной величиной с некоторым законом распределения:
Если известна дисперсия для каждой компоненты вектора ${{\delta }}{{D}_{{exp}}}$ (с точностью до постоянной), то для решения системы уравнений (2) может быть использован известный метод наименьших квадратов (МНК) с весами.
Уравнение (1) является уравнением Фредгольма 1-го рода и имеет плохую обусловленность, которая выражается в том, что даже малые изменения величины $D\left( x \right)$ могут приводить к большим изменениям $f\left( E \right).$ Поскольку уравнение (2) является дискретным представлением (1), то оно также чувствительно ко входным данным, поэтому для решения обратной задачи стандартный МНК дополняется регуляризующими алгоритмами [10‒12], например, регуляризацией Тихонова [13]. Таким образом, задачу (2) можно переписать следующим образом:
(4)
$\left\{ {\begin{array}{*{20}{c}} {{{{\min }}_{f}}(\theta \left[ f \right])} \\ {\theta \left[ f \right] = {{{\left\| {{{S}^{{\frac{1}{2}}}}\left( {{{D}_{{exp}}} - df} \right)} \right\|}}^{2}} + \alpha {{{\left\| f \right\|}}^{2}}} \end{array}~,} \right.$(5)
${{f}_{{rest}}}\left( \alpha \right) = {{({{d}^{T}}Sd + \alpha E)}^{{ - 1}}}{{d}^{T}}S{{D}_{{exp}}},$Целью данной работы было исследование различных способов выбора параметра регуляризации Тихонова для восстановления энергетических спектров пучков электронов по известным дозовым распределениям. Степень успешности решения поставленной задачи оценивалось по близости истинного и восстановленного глубинных дозовых распределений.
МАТЕРИАЛЫ И МЕТОДЫ
Расчет глубинных дозовых распределений
В качестве исходных спектров f, для которых оценивалась точность восстановления, были взяты спектры ускорителя УЭЛР-10-15С [15] для четырех различных режимов его работы, которые представлены на рис. 1а. Моделирование этих режимов проводилось с использованием программного пакета Geant4. Спектр источника задавался по набору точек с помощью линейной интерполяции. Источник имел форму квадрата со стороной 12 см.
Рис. 1.
Энергетические спектры ускорителя УЭЛР-10-15С для четырех рабочих режимов (1–4) (а). Глубинные дозовые распределения в параллелепипеде, соответствующие четырем рабочим режимам ускорителя (б).
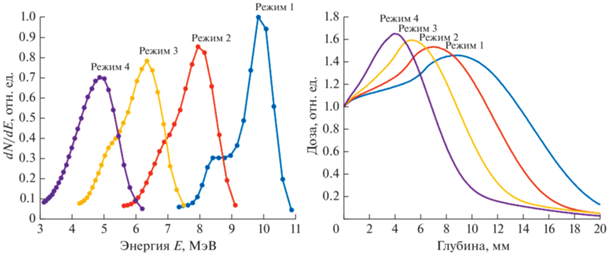
Для соответствующих энергетических спектров f с использованием компьютерного моделирования, основанного на методе Монте-Карло с помощью программного кода Geant4, были рассчитаны глубинные дозовые распределения D, представленные на рис. 1б.
Распределение дозы рассчитывалось в алюминиевом параллелепипеде с поперечными размерами 2 × 2 см и толщиной 3 см. Источник электронного излучения был представлен в виде квадратной площадки с ребром 3 см. Ось параллелепипеда совпадала с первоначальным направлением пучка электронов. Для измерения дозовых распределений параллелепипед равномерно разбивался на 300 слоев одинаковой толщины 0.1 мм, в каждом из которых проводилось вычисление поглощенной энергии. Спектр источника задавался по набору точек с помощью линейной интерполяции (рис. 1а). Источник имел форму квадрата со стороной 12 см.
Для нахождения значений доз в столбцах матрицы d также использовалось компьютерное моделирование на Geant4. В данной работе в качестве базисных функций спектра пучка Ij(E) использовались прямоугольные функций различной ширины ΔE от 0.1 до 0.5 МэВ с шагом 0.1 МэВ, расположенных в интервале от 0 до 12 МэВ. Количество историй при расчете дозовых распределений для каждой базисной функции ${{I}_{j}}\left( E \right)$ составляло 109 электронов.
Подбор параметра регуляризации
При использовании метода регуляризации Тихонова важным моментом является выбор значения параметра регуляризации α, поскольку слишком малый параметр может привести к недостаточной обусловленности системы, а выбор слишком большого значения – к решению ${{f}_{{rest}}},$ далекому от истинного значения f. В литературе представлены различные методы по определению параметра регуляризации [16–18].
Метод поправки, описанный в работе [16], предлагает сначала выбрать некоторое начальное значение параметра регуляризации α1, которое заведомо меньше искомого, затем сформировать набор из $K$ значений параметра ${{\alpha }_{k}}\left( {k = 1:K} \right),$ которые связаны следующим образом:
где $\beta $ – постоянный множитель $\left( {\beta > 1} \right)$ и $K~$ выбираются так, чтобы искомое значение параметра регуляризации было меньше ${{\alpha }_{K}}.$ Затем для каждого ${{\alpha }_{k}}$ предлагается найти соответствующее ему решение задачи (4) – ${{f}_{{rest}}}\left( {{{\alpha }_{k}}} \right).$ После чего выбрать такое значение параметра ${{\alpha }_{k}},$ при котором изменение решения $\left\| {{{f}_{{rest}}}\left( {{{\alpha }_{k}}} \right) - {{f}_{{rest}}}\left( {{{\alpha }_{{k - 1}}}} \right)} \right\|$ – минимально.В схожем методе относительной поправки [16] предлагается выбрать такое значение параметра регуляризации ${{\alpha }_{k}},$ при котором относительное изменение решения $\left\| {{{f}_{{rest}}}\left( {{{\alpha }_{k}}} \right)} \right. - {{\left. {{{f}_{{rest}}}\left( {{{\alpha }_{{k - 1}}}} \right)} \right\|} \mathord{\left/ {\vphantom {{\left. {{{f}_{{rest}}}\left( {{{\alpha }_{{k - 1}}}} \right)} \right\|} {\left\| {{{f}_{{rest}}}\left( {{{\alpha }_{k}}} \right)} \right\|}}} \right. \kern-0em} {\left\| {{{f}_{{rest}}}\left( {{{\alpha }_{k}}} \right)} \right\|}}$ – минимально.
Квазиоптимальный метод, описанный в [17], предлагает выбрать такое значение параметра α, при котором достигается локальный минимум функции $\Psi \left( \alpha \right) = {{\left\| {\alpha \frac{{d{{f}_{{rest}}}\left( \alpha \right)}}{{d\alpha }}} \right\|}^{2}}.$ Если локальных минимумов несколько, то рекомендуется выбирать наименьшее значение параметра, доставляющее минимум.
Метод невязки [18] заключается в подборе значения параметра регуляризации α таким образом, чтобы точно выполнялось следующее равенство:
В данной работе исследовались все методы, описанные выше, также сравнивались с “эталонным” методом, заключающийся в нахождении такого значения параметра регуляризации α, при котором относительное отклонение $\frac{{\left\| {{{f}_{{rest}}}\left( \alpha \right) - f} \right\|}}{{\left\| f \right\|}}~$ спектра минимально, прямым перебором значений. Такое сравнение позволяет оценить ошибки, вызванные приближением исходного спектра f прямоугольниками, и величину ошибки восстановления спектра, вызванной ошибкой измерения ${{\delta }}{{D}_{{exp}}}.$
Моделирование погрешности измерений
Как было отмечено ранее, дозовые распределения, полученные экспериментальным путем, всегда известны с некоторой ошибкой ${{\delta }}{{D}_{{exp}}},$ поэтому для симуляции ${{\delta }}{{D}_{{exp}}}$ результатов измерений дозового распределения D с коэффициентом вариации σ использовался генератор псевдослучайных чисел со стандартным нормальным распределением $~N\left( {0,1} \right){\text{:}}$
где ${{\sigma }^{2}}$ характеризует погрешность измерений.Розыгрыш случайной величины осуществлялся для каждой компоненты вектора D независимо. После такого моделирования экспериментальной погрешности по формуле (5) находился восстановленный спектр frest и далее вычислялось соответствующее восстановленному спектру дозовое распределение${{D}_{{rest}}} = d{{f}_{{rest}}}.$ В работе проводилось сравнение восстановленных спектров frest c исходными f, а также для оценки степени успешности решения поставленной задачи проводилось сравнение истинных D и восстановленных Drest глубинных дозовых распределений. Процедура проводилась многократно и вычислялись средние значения относительных ошибок восстановленного спектра и дозового распределения:
(6)
$\delta {{f}_{{rest}}} = \frac{{\left\| {{{f}_{{rest}}} - f} \right\|}}{{\left\| f \right\|}} \cdot 100\% \,\,\,\,{\text{и}}\,\,\,\,~\delta {{D}_{{rest}}} = \frac{{\left\| {{{D}_{{rest}}} - D} \right\|}}{{\left\| D \right\|}} \cdot 100\% ~,$Значения средних ошибок восстановленного спектра $\delta {{f}_{{rest}}}$ и дозового распределения $\delta {{D}_{{rest}}}$ были найдены для всех приведенных выше режимов работы ускорителя УЭЛР-10-15С со стандартным отклонением среднего значения $\sigma ,$ варьирующемся в диапазоне от 1 до 5%, и ΔE, варьирующейся в диапазоне энергий от 0.1 до 0.5 МэВ.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Ниже представлена табл. 1 со значениями ошибки восстановленных спектров $\delta {{f}_{{rest}}}$ для прямоугольных функций шириной ΔE, равной 0.5 МэВ с $\sigma ,$ варьирующейся от 1 до 5%, для всех четырех рабочих режимов ускорителя с погрешностью не более 2%.
Таблица 1.
Относительные ошибки восстановления спектра пучка электронов для разных режимов ускорителя УЭЛР-10-15С при различных значениях σ
| Режим исходного спектра | σ, % | Относительная ошибка восстановленного спектра, % | ||||
|---|---|---|---|---|---|---|
| αэтал2 | αн3 | αп4 | αоп5 | αквази6 | ||
| Режим 4 | 1 | 13.1 | 23.9 | 24.3 | 26 | 24 |
| 2 | 16.8 | 31.6 | 34.2 | 37.1 | 34.7 | |
| 3 | 20.1 | 36.2 | 40.7 | 43.3 | 42.6 | |
| 4 | 21.3 | 40.9 | 45.6 | 46.5 | 46.2 | |
| 5 | 21.9 | 41.8 | 48.9 | 50.3 | 49.6 | |
| Режим 3 | 1 | 21.9 | 34.1 | 39 | 41.2 | 39.2 |
| 2 | 25.8 | 42.5 | 50.4 | 51.1 | 48.3 | |
| 3 | 27.9 | 45.7 | 56 | 55 | 53.6 | |
| 4 | 30.3 | 50.5 | 59.2 | 57.8 | 59.5 | |
| 5 | 31.3 | 54.1 | 63.8 | 64.1 | 62.9 | |
| Режим 2 | 1 | 27.1 | 42.7 | 48.5 | 50.9 | 49.9 |
| 2 | 33.7 | 56 | 59.4 | 57.8 | 59.9 | |
| 3 | 35.3 | 57.3 | 67.1 | 67.9 | 66.8 | |
| 4 | 37.9 | 63 | 69.9 | 69.5 | 70.2 | |
| 5 | 37.5 | 69.1 | 74.1 | 72.6 | 74.5 | |
| Режим 1 | 1 | 53.4 | 79.8 | 85.4 | 86.8 | 82.8 |
| 2 | 59.6 | 96.5 | 92.1 | 94.1 | 92.8 | |
| 3 | 63.5 | 98 | 92.4 | 103 | 97.4 | |
| 4 | 64 | 105.3 | 95.8 | 106.2 | 97 | |
| 5 | 64.5 | 108.2 | 100.1 | 107.8 | 104.7 | |
2 αэтал – параметр регуляризации, рассчитанный по “эталонному” методу. 3 αн – параметр регуляризации, рассчитанный по методу невязок. 4 αп – параметр регуляризации, рассчитанный по методу поправо. 5 αоп – параметр регуляризации, рассчитанный по методу относительных поправок. 6 αквази – параметр регуляризации, рассчитанный по квазиоптимальному методу.
В качестве примера на рис. 2 приведены восстановленные спектры для одного и того же дозового распределения, рассчитанные по формуле (5) для различных методов выбора параметра регуляризации Тихонова.
Рис. 2.
Восстановленные энергетические спектры ускорителя УЭЛР-10-15С для σ = 1% и $\Delta E$ = 0.5 МэВ в случае работы ускорителя в режиме 4 (а), 3 (б), 2 (в), 1 (г).

Из табл. 1 видно, что погрешность восстановления спектров $\delta {{f}_{{rest}}}$ для режимов 2–4 в случае выбора параметра регуляризации методом невязки меньше, чем погрешность восстановления для остальных методов. Это можно объяснить тем, что метод невязки учитывает при подборе параметра регуляризации информацию об ошибках $\delta {{D}_{{exp}}},$ что выгодно отличает его от остальных методов. Для всех значений σ в диапазоне от 1 до 5% значения $\delta {{f}_{{rest}}}$ при выборе метода невязки в среднем ниже на 8% по сравнению с методом поправок, на 12% – методом относительных поправок и на 9% – с квазиоптимальным методом. Необходимо отметить, что для режима 1 все методы выбора параметра регуляризации, включая метод невязки и эталонный, дают высокую погрешность восстановления спектра.
Также видно, что точность восстановления спектров различна для разных режимов независимо от выбора параметра регуляризации. Так, с увеличением σ от 1 до 5% для метода невязки погрешность восстановления энергетических спектров увеличивается с 24 до 42% при работе ускорителя в режиме 4, и с 34 до 54%, с 43 до 69% и с 80 до 108% для режимов 3, 2 и 1, соответственно. В свою очередь, при прямом подборе параметра регуляризации αэтал под истинный спектр frest погрешность восстановления $\delta {{f}_{{rest}}}$ увеличивается с 13 до 22%, с 22 до 31%, с 27 до 38% и с 53 до 65% для соответствующих режимов 4–1.
Различия в точности восстановления для разных энергетических режимов ускорителя могут быть связаны с тем, что профиль спектра электронного пучка принимает более сложную форму с увеличением энергии электронов (рис. 1а). Так, для спектра ускорителя, работающего в режиме 1, сглаживание, вызванное регуляризацией, вносит большую ошибку, чем для спектров, работающих на более низких энергиях при любых параметрах регуляризации.
Также из анализа данных относительных ошибок восстановленных спектров $\delta {{f}_{{rest}}}$ относительно исходного спектра режима 1–4 ускорителя УЭЛР-10-15С было установлено, что выбор ширины прямоугольных функций ΔE от 0.1 до 0.5 МэВ влияет на погрешность восстановленных спектров не более чем на 3%. С одной стороны уменьшение ширины прямоугольных функций ΔE лучше приближает спектр пучка, с другой стороны, тем ближе оказываются кривые дозовых распределений и тем сложнее их различить. Кроме того, уменьшение ΔE означает увеличение количества прямоугольных функций, что влечет к избыточности данных в системе, а следовательно, к ее плохой обусловленности (4).
Аналогичные сравнения относительных ошибок $\delta {{D}_{{rest}}}$ при различном выборе параметра регуляризации были проведены и для восстановленных дозовых распределений. Результаты представлены в табл. 2.
Таблица 2.
Данные относительных ошибок восстановления глубинных дозовых распределений для разных режимов ускорителя УЭЛР-10-15С
| Режим исходного спектра | σ, % | Относительная ошибка восстановленного дозового распределения, % | ||||
|---|---|---|---|---|---|---|
| αэтал | αн | αп | αоп | αквази | ||
| Режим 4 | 1 | 1 | 1.1 | 1 | 1 | 1 |
| 2 | 1.9 | 2.2 | 2 | 2 | 2 | |
| 3 | 2.9 | 3.2 | 2.9 | 3.1 | 2.9 | |
| 4 | 3.9 | 4.3 | 3.9 | 3.9 | 3.8 | |
| 5 | 4.9 | 5.3 | 4.8 | 4.9 | 4.7 | |
| Режим 3 | 1 | 1 | 1.1 | 1 | 1 | 1 |
| 2 | 1.9 | 2.2 | 2 | 2 | 1.9 | |
| 3 | 2.9 | 3.2 | 2.9 | 2.9 | 2.9 | |
| 4 | 3.9 | 4.3 | 3.8 | 3.9 | 3.8 | |
| 5 | 4.8 | 5.3 | 4.8 | 4.8 | 4.8 | |
| Режим 2 | 1 | 1 | 1.1 | 1 | 1 | 1 |
| 2 | 1.9 | 2.2 | 1.9 | 2 | 2 | |
| 3 | 2.9 | 3.2 | 2.9 | 2.9 | 2.9 | |
| 4 | 3.8 | 4.3 | 3.8 | 3.9 | 3.8 | |
| 5 | 4.7 | 5.3 | 4.7 | 4.8 | 4.7 | |
| Режим 1 | 1 | 1 | 1.1 | 1 | 1 | 1 |
| 2 | 1.9 | 2.2 | 2 | 2 | 2 | |
| 3 | 2.9 | 3.2 | 2.9 | 2.9 | 2.9 | |
| 4 | 3.9 | 4.3 | 3.8 | 3.9 | 3.8 | |
| 5 | 4.8 | 5.3 | 4.8 | 4.8 | 4.8 | |
Было установлено, что изменение ширины ΔE от 0.1 до 0.5 МэВ прямоугольных базисных функций в восстановленных спектрах frest оказывает влияния не более 1% на ошибки $\delta {{D}_{{rest}}}$ восстановленных по данным спектрам дозовых распределений Drest.
Можно отметить, что большим ошибкам $\delta {{f}_{{rest}}}$ восстановленных спектров соответствуют малые ошибки дозовых распределений $\delta {{D}_{{rest}}}$ (табл. 1 и 2). Так, относительные ошибки восстановленных спектров $\delta {{f}_{{rest}}}$ в случае режима 4 работы ускорителя с увеличением $\sigma $ от 1 до 5% растут в среднем от 24 до 50% для всех параметров регуляризации, а относительные ошибки соответствующих дозовых распределений $\delta {{D}_{{rest}}},$ реконструированные по восстановленным спектрам, растут от 1 до 5%. Это можно объяснить тем, что для близких значений энергий кривые дозовых распределений похожи, тогда, если соседние прямоугольные функции при разбиении спектра пучка будут различаться сильно, то соответствующие глубинные распределения будут слабо различимы. Также можно отметить, что погрешности $\delta {{D}_{{rest}}}$ сопоставимы с внесенными искусственно экспериментальными погрешностями σ в дозовых распределениях Dexp. Таким образом, восстановленные дозовых распределений в пределах погрешности не отличается от экспериментальных значений.
На рис. 3 для режима 4 ускорителя УЭЛР-10-15С рассмотрены дисперсии спектра и соответствующего глубинного дозового распределения. Дисперсия $Var\left( {{{{\tilde {f}}}_{i}}} \right),$ где $\tilde {f}$ – случайный вектор спектра пучка со средними значениями компонент равными f и коэффициентом вариации $\varphi ,$ вычислялась следующим образом$:$
Рис. 3.
Исходный спектр f пучка электронов УЭЛР-10-15С для режима 4 (синяя сплошная кривая) с ${{\varphi }_{{min}}}$ = 24% (красная пунктирная кривая) и с ${{\varphi }_{{max}}}$ = 42% (черная точечная кривая) (а). Глубинное дозовое распределение D (синяя сплошная кривая), соответствующего исходного спектра f, с соответствующими интервалами для дисперсии (б).
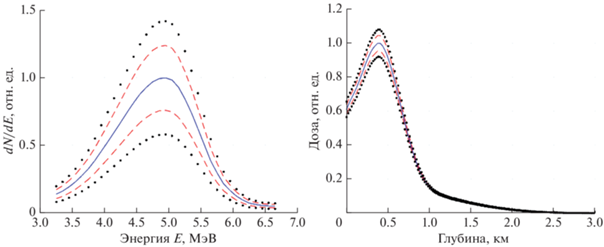
Покажем, что коэффициент вариации i-й компоненты$\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }}_{i}}} \right)$ дозового распределения $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} = d\tilde {f}$ будет меньше $\varphi .$ Дисперсия 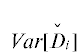 примет следующий вид:
примет следующий вид:
(7)
$\begin{gathered} Var[{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }}_{i}}] = Var\left[ {\sum\limits_j {\left( {{{d}_{{ji}}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{f} }}_{j}}} \right)} } \right] = \sum\limits_j {d_{{ij}}^{2}Var\left[ {{{f}_{j}}} \right]} = \sum\limits_j {{{{({{d}_{{ji}}}{{f}_{j}}\varphi )}}^{2}}} = \\ = {{\varphi }^{2}}\sum\limits_j {{{{({{d}_{{ji}}}{{f}_{j}})}}^{2}}} = {{\varphi }^{2}}{{\left( {\sum\limits_j {{{d}_{{ji}}}{{f}_{j}}} } \right)}^{2}} - {{\varphi }^{2}}\sum\limits_j {\sum\limits_k {{{d}_{{ji}}}{{f}_{j}}{{d}_{{ki}}}{{f}_{k}}} } = {{\varphi }^{2}}D_{i}^{2} - {\text{\;}}{{\varphi }^{2}}\sum\limits_j {\sum\limits_k {{{d}_{{ji}}}{{f}_{j}}{{d}_{{ki}}}{{f}_{k}}} } , \\ \end{gathered} $Отметим, что элементы матрицы d и компоненты вектора f по физическому смыслу всегда неотрицательны, а значит $Var[{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }_{i}}] \leqslant {{\varphi }^{2}}D_{i}^{2},$ т.е. коэффициент вариации для дозового распределения $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} $ меньше, чем коэффициент вариации для спектра $\tilde {f}$. В качестве примера, на рис. 3 приведен спектр пучка f с интервалом для коэффициента вариации дисперсии ${{\varphi }_{{min}}}$ = 24% и ${{\varphi }_{{mах}}} = $ 42% для режима 4 работы ускорителя УЭЛР-10-15С. Интервалы по $\varphi $ для спектров были выбраны с учетом данных из табл. 1 по относительным погрешностям восстановленных спектров ${{\delta }}{{f}_{{rest}}}$ ускорителя для параметра регуляризации, выбранного методом невязки.
На рис. 3б показано глубинное дозовое распределение D соответствующего исходного спектра f для режима 4 с интервалами для дисперсии, которые определялись по формуле (7). Максимальная величина интервала для коэффициента вариации дисперсии глубинного дозового распределения не превышала 4 и 8%, соответственно для ${{\varphi }_{{min}}}$ и ${{\varphi }_{{max}}}.$ Для режимов 3–1, интервал по коэффициенту вариации дисперсии глубинного распределения составил 6 и 10, 7 и 12, 10 и 15%, соответственно. Возрастание дисперсии связано с соответствующим увеличением относительной ошибки восстановленных спектров ${{\delta }}{{f}_{{rest}}}$.
Таким образом, метод регуляризации Тихонова можно успешно использовать для синтеза спектров по заданным дозовым распределениям с погрешностью не более 15%.
ЗАКЛЮЧЕНИЕ
Предложенный в данной работе метод восстановления спектрального состава пучка электронов успешно производит реконструкцию спектра по глубинным дозовым распределениям с использованием регуляризации Тихонова.
Исследование влияния различных параметров регуляризации Тихонова показало, что погрешность восстановления спектров в случае выбора параметра регуляризации методом невязки в среднем ниже на 10% по сравнению с другими методами. Показано, что с увеличением σ от 1 до 5% точность восстановления энергетических спектров в среднем уменьшается примерно на 20% для всех методов определения параметра регуляризации относительно исходных спектров.
Показано, что восстановление более сложного вида спектра происходит с большей погрешностью. Выбор ширины прямоугольных функций ΔE от 0.1 до 0.5 МэВ влияет на погрешность восстановленных спектров не более чем на 3%, а на погрешность соответствующих восстановленных по ним дозовых распределений не более 1%.
Была показана достаточная эффективность метода регуляризации Тихонова для задач синтеза спектров с заданными дозовыми распределениями. Точность реконструкции глубинных дозовых распределений по восстановленным энергетическим спектрам составляет порядка 85–95% в зависимости от сложности вида спектра электронного пучка ускорителя и выбора параметра регуляризации.
Исследование выполнено при поддержке Междисциплинарной научно-образовательной школы Московского университета “Фотонные и квантовые технологии. Цифровая медицина”.
Список литературы
Chernyaev A.P., Varzar S.M., Borschegovskaya P.Y. et al. // Phys. Part. Nucl. Lett. 2017. V. 13. No. 7. P. 988.
Chernyaev A.P., Kolyvanova M.A., Borshchegovskaya P.Yu. // Moscow Univ. Phys. Bull. 2015. V. 70. No. 6. P. 457.
Близнюк У.А., Авдюхина В.М., Борщеговская П.У. и др. // Изв. РАН Сер. физ. 2018. Т. 82. № 6. С. 824; Bliznyuk U.A., Avdyukhina V.M., Borchegovskaya P.U. et al. // Bull. Russ. Acad. Sci. Phys. 2018. V. 82. No. 6. P. 740.
Li G., Wu A., Lin H., Wu Y. // Proc. 7th APCMBE (Beijing, 2008). P. 451.
Gui L., Hui L., Ai-Dong W. et al. // Chin. Phys. Lett. 2008. V. 25. No. 7. P. 2710.
Vega J.M., Guirado D., Vilches M. et al. // Radiother. Oncol. 2008. V. 86. P. 109.
Kozyrev A.V., Kozhevnikov V.Yu., Vorobyov M.S. et al. // Laser Part. Beams. 2015. V. 33. P. 183.
Близнюк У.А., Авдюхина В.М., Борщеговская П.У. и др. // Изв. РАН. Сер. физ. 2021. Т. 85. № 10. С. 1430; Bliznyuk U.A., Avdyukhina V.M., Borshchegovskaya P.Yu. et al. // Bull. Russ. Acad. Sci. Phys. 2021. V. 85. No. 10. P. 1108.
Carletti C., Meoli P., Cravero W. // Phys. Med. Biol. 2006. V. 51. No. 16. P. 3941.
Visbal J.H.W., Costa A.M. // Radiat. Phys. Chem. 2019. V. 162. P. 31.
Wazwaz A.M. // Comput. Math. Appl. 2011. V. 61. No. 10. P. 2981.
Xu Y., Pei Y., Dong F. // Flow Meas. Instrum. 2016. V. 50. P. 1.
Тихонов А.Н. // ДАН СССР. 1965. Т. 163. № 3. С. 591.
Василенко Г.И., Тараторин А.М. Восстановление изображений. М.: Радио и связь, 1986. 304 с.
Ханкин В.В. Экспериментальное исследование динамики пучков в импульсном линейном ускорителе и разрезном микротроне. Дис. … канд. физ.-мат. наук. М.: МГУ, 2020. 123 с.
Гарт Л.Л., Манойло М.В. // Системні дослідження та інформаційні технології. 2015. № 1. С. 99.
Леонов А.С. // Сибирск. матем. журн. 1993. Т. 34. № 4. С. 117.
Морозов В.А. // Вычисл. матем. и матем. физ. 1968. Т. 8. № 2. С. 295.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


