Известия РАН. Серия физическая, 2022, T. 86, № 4, стр. 476-481
Динамика керровского вращения макроскопического спинового момента в квантово-холловском ферромагнетике
С. М. Дикман *
Федеральное государственное бюджетное учреждение науки
Институт физики твердого тела имени Ю.А. Осипьяна Российской академии наук
Черноголовка, Россия
* E-mail: dickmann@issp.ac.ru
Поступила в редакцию 15.11.2021
После доработки 06.12.2021
Принята к публикации 22.12.2021
- EDN: CVFWZF
- DOI: 10.31857/S036767652204007X
Аннотация
Предложен макроскопический подход к описанию системы, которая обычно исследуется микроскопически. Объектом изучения является двумерный электронный газ в одном из своих “квантово-холловских” состояний. Показано, что движение макроскопического объекта – коллективного спинового момента в “квантово-холловском ферромагнетике” может изучаться феноменологически подобно тому, как это происходит при использовании уравнения Ландау–Лифшица для описания движения магнитного момента в классическом магнетике.
Двумерный электронный газ (two-dimensional electron gas, 2DEG), состоящий только из электронов проводимости, представляет собой уникальный квантовый объект для прямого изучения магнитных явлений, типичных для “классических” (или “обменных”) магнетиков с локализованными спиновыми моментами. Хотя существует довольно много теоретических работ, в которых предсказывалось существование остаточной намагниченности в 2DEG, последняя экспериментально до сих пор не обнаружена. Тем не менее, при наличии приложенного внешнего магнитного поля 2DEG представляет собой квантово-холловскую систему, (quantum Hall system – QHS) и обладает многими свойствами, которые наблюдаются экспериментально и которые можно охарактеризовать как проявление квантово-холловского магнетизма. К числу коллективных магнитных явлений, изучаемых экспериментально и теоретически в QHS и определяемых только лишь кулоновским взаимодействием электронов в 2DEG, можно отнести, например, возбуждение и наблюдение спиновых волн [1–5], открытие и исследование скирмионов [6–8], открытие и изучение стонеровской неустойчивости [9–11] и наблюдение керровского вращения плоскости поляризации в “квантово-холловском ферромагнетике” [12–14]. Описание динамики керровского вращения является предметом, которому посвящена предлагаемая теоретическая статья. При этом возможен как микроскопический, так и макроскопический подходы. Микроскопический (или квантово-механический) подход основан на использовании ab initio кулоновского гамильтониана для электронов 2DEG в многоэлектронном уравнения Шредингера. Со своей стороны макроскопический подход оправдан в силу того, что исследуемое явление является макроскопическим, т.е. сходным тому, что наблюдается в обычных обменных ферромагнетиках. Для теоретического исследования последних как правило используется либо чисто феноменологический подход, либо квантово-механический, но основанный на модельном гамильтониане, например, на гамильтониане Гейзенберга. Микроскопический же подход в исследовании 2DEG является, разумеется, наиболее полным и последовательным. Внешние поля в 2DEG, такие как пространственные флуктуации электростатического потенциала или действующие на спин электронов микроскопические спин-орбитальное и сверхтонкое взаимодействия, определяющие релаксационные процессы в 2DEG, также рассматриваются непосредственно, хотя и в рамках теории возмущений. Этот подход был развит во многих известных работах (см., например, публикации [15‒17]). В применении к керровскому вращению в квантово-холловской системе в работах [18, 19].
В данной статье мы используем чисто феноменологический подход. В этом контексте обращаются обычно к уравнению, имеющему вид [20]:
(1)
${{\partial{ \vec {S}}} \mathord{\left/ {\vphantom {{\partial{ \vec {S}}} {\partial t}}} \right. \kern-0em} {\partial t}} = - g{{{{\mu }}}_{B}}\vec {S} \times \vec {B} - \vec {R}.$Здесь первый член в правой части представляет собой нулевое приближение по обратной величине обменной энергии ферромагнетика, в котором предполагается, что магнитный момент (в 2DEG это макроскопически большой полный спин электронов) является абсолютно жестким вектором с неизменной величиной S. Этот член описывает прецессию момента и его вид в этом приближении однозначно следует из концепции пропорциональности спина $\vec {S}$ моменту механического ротатора. Соответственно gµBB – это зеемановская энергия одного электрона, где µB = = e/mec – магнетон Бора, а g – фактор Ланде.
Вид вектора $\vec {R},$ отвечающего затуханию прецессии спинового момента, может быть также найден из простых феноменологических соображений. Поскольку можно доказать, что всегда в равновесии спиновый момент направлен параллельно “эффективному” магнитному полю, а последнее в 2DEG фактически равно просто полю $\vec {B},$ то $\vec {R}$ выбирается направленным от $\vec {S}$ к $\vec {R}.$ В условиях абсолютной спиновой жесткости этот вектор не должен менять величину полного спина, т.е. уравнение (1) всегда должно удовлетворять условию ${{\vec {S}\partial{ \vec {S}}} \mathord{\left/ {\vphantom {{\vec {S}\partial{ \vec {S}}} {\partial t}}} \right. \kern-0em} {\partial t}}$ ≡ 0 (или $\vec {S}\vec {R}$ ≡ 0) Тогда однозначно с точностью до неизвестного коэффициента получаем:
(2)
$\vec {R} = {{\vec {R}}_{{L--L}}} = {{\lambda }_{{LL}}}\vec {S} \times (\vec {S} \times \vec {B}).$Подстановка этого выражения в уравнение (1) дает хорошо известное феноменологическое уравнение Ландау–Лифшица [20]. Движение, описываемое этим уравнением, прецессия и затухание, показаны графически на рис. 1а. Авторы [20] считали, что в условиях абсолютной спиновой жесткости затухание прецессии (приближение $\vec {S}$ к $\vec {B}$) связано с релятивистским взаимодействием более высокого порядка, которое значительно слабее обменного и не влияет на спиновую жесткость. Иными словами, всегда должен выполняться закон сохранения для величины S2. Затухание прецессии сопровождается сравнительно слабыми процессами, приводящими к диссипации зеемановской энергии |g|μBB|Sz(∞) – Sz(0)| вследствие приближения компоненты спина Sz(t) к своему равновесному значению Sz(∞) при сохранении величины S2 (ось z считается направленной вдоль $\vec {B}$).
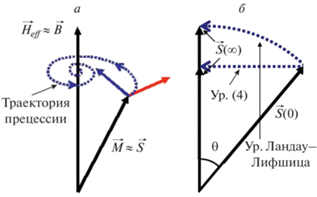
Рис. 1.
Иллюстрация движения полного спина системы; красная стрелка соответствует первому (прецессионному) члену в макроскопическом уравнении движения (1), синяя стрелка второму члену, отвечающему за затухание прецессии (а). Затухание в координатной системе, прецессирующей вместе со спиновым моментом; синие пунктирные линии это траектории $\vec {S}$(t), меняющиеся от $\vec {S}$(0) к $\vec {S}$(∞), показанные для уравнения Ландау–Лифшица (дуга, см. формулы (1) и (2)) и для уравнения (1) с членом (4) (горизонтальная прямая) (б).
Для обычных диэлектрических магнетиков подобное условие почти всегда выполнено, но для электронного газа оно не применимо. Действительно, жесткость ферромагнетика определяется отношением характерной обменной энергии к величине характерной одноэлектронной и это отношение в QHS на два–три порядка меньше чем в обычном ферромагнетике, а именно, характерная обменная энергия, будучи в 2DEG того же порядка, что и характерная кулоновская энергия, есть величина ∼EC = αe2/εlB, где α < 1 – формфактор, возникающий из-за конечности толщины 2DEG, а ε и lB соответственно диэлектрическая константа и магнитная длина. Характерная же одноэлектронная энергия – это, очевидно, зеемановская энергия, входящая в “прецессионный” член уравнения (1). Мерой жесткости является отношение
(3)
${{r}_{s}} = {{{{E}_{C}}} \mathord{\left/ {\vphantom {{{{E}_{C}}} {\left| {g{{\mu }_{B}}B} \right|}}} \right. \kern-0em} {\left| {g{{\mu }_{B}}B} \right|}}.$В QHS, созданной в гетероструктуре на основе GaAs, rs ∼ 50–100. Это на несколько порядков меньше, чем в классических магнетиках. Если отбросить условие абсолютной жесткости, то феноменологический подход также вполне возможен. Очевидно, что к вектору (2), описывающему релаксацию, надо добавить другой вектор, неколлинеарный ему, но тоже в плоскости ($\vec {B},$ $\vec {S}$) и тоже направленный от $\vec {S}$ к $\vec {B}.$ Простейший вариант это, имея по-прежнему в распоряжении только $\vec {B}$ и $\vec {S},$ рассмотреть дополнительный вектор
В отличие от $\vec {R}$L–L этот вектор сохраняет не спиновую жесткость (величину S), а зеемановскую энергию (компоненту Sz). Понятно, что в общем виде любые взаимодействия спина с внешними полями, приводящие к затуханию прецессии, всегда, будут описываться комбинацией
На рис. 1б в координатной системе, прецессирующей вместе со спиновым моментом, пунктирными линиями показаны оба типа релаксации.
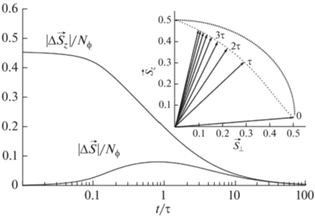
Задача о движении спинового момента сводится теперь к определению констант λL–L и λQH, которые, вообще говоря, должны быть найдены с помощью микроскопического рассмотрения. При этом естественно, что из множества взаимодействий следует выбрать обеспечивающее наиболее быструю релаксацию. В ранних работах изучались механизмы релаксации глобальной спин-поворотной (голдстоуновской) моды в 2DEG, связанные с наличием пространственных флуктуаций внешнего эффективного электростатического потенциала в гетероструктуре GaAs/AlGaAs в совокупности со спин-орбитальным [21] или сверхтонким [22] взаимодействиями. В обоих случаях при микроскопическом подходе оказывается, что релаксация происходит при одновременном одинаковом изменении спиновых чисел S и Sz, а именно элементарный процесс приводит к изменению δSz = = –δS = 1 (учтено то, что g-фактор в GaAs отрицателен). При этом в феноменологическом уравнении должны присутствовать оба “релаксационных” вектора в правой части формулы (5). Пример траектории изменения момента $\vec {S}$ в этом случае показан на вставке на рис. 2. В основной части этого рисунка показано изменение от времени величин отклонений спиновых чисел от их равновесных значений: ∆Sz = S0z – Sz и ∆S = S0 – S, где для равновесного вектора S0 имеем S0z = S0. Характерное время релаксации составляет величину порядка 100 нс или даже больше. Причем, элементарный микроскопический процесс – это превращение пары голдстоуновских спиновых магнитоэкситонов (с волновыми векторами строго, равными нулю), каждый из которых имеет энергию |gµBB|, в один спин-волновой магнитоэкситон, имеющий энергию
(6)
${{E}_{{sw}}} = \left| {g{{\mu }_{B}}B} \right| + {{{{q}^{2}}} \mathord{\left/ {\vphantom {{{{q}^{2}}} {2{{M}_{x}}}}} \right. \kern-0em} {2{{M}_{x}}}}.$Рис. 2.
Изменение во времени полного спина квантово-холловского ферромагнетика $\vec {S}$(t) при условии, что важны оба “релаксационных” слагаемых в уравнении (5) см. текст. В начальный момент спин как целое отклонен на некоторый угол от направления поля $\vec {B},$ близкий к 90°. ∆Sz(t) = |$\vec {S}$(0)| – Sz(t) (Nϕ – число квантов магнитного потока в системе). На вставке показано положение вектора $\vec {S}$(t) в различные моменты t = 0, τ, 2τ, 3τ, … Точечная линия – дуга, которая являлась бы траекторией конца вектора $\vec {S}$(t) в соответствии с уравнением Ландау–Лифшица.
Здесь $\vec {q}$ волновой вектор спин-волнового магнитоэкситона, который мы будем рассматривать в единицах 1/lB, а Mx ∝ EC–1 спин-волновая “масса” (как известно [3, 4, 16, 17], спектр спин-волнового магнитоэкситона, определяемый кулоновским взаимодействием, квадратичен при малых q). При таком переходе спиновые числа и полный волновой вектор системы не сохраняются, а сохранение энергии сводится к уравнению
(7)
$\left| {g{{\mu }_{B}}B} \right| = {{{{q}^{2}}} \mathord{\left/ {\vphantom {{{{q}^{2}}} {2{{M}_{x}}}}} \right. \kern-0em} {2{{M}_{x}}}}.$В последующем, однако, оказалось, что экспериментально затухание керровских осцилляций (релаксация поперечной компоненты ${{\vec {S}}_{ \bot }}$ = (Sx, Sу)) протекает гораздо быстрее – за время порядка 10–15 нс [12–14]. То есть, очевидно, что для поперечной релаксации спинового момента существует более быстрый механизм. Такой механизм определяется наличием слабого “плавного” магнитного беспорядка в системе, а именно плавными пространственными флуктуациями эффективного g-фактора для 2D электронов в квантовой яме [18] или плавными флуктуациями локальной намагниченности ядер [19]. Микроскопически этот релаксационный канал сводится к элементарному одноэкситонному процессу превращения голдстоуновского магнитоэкситона в спин-волновой с ненулевым, но формально стремящемся к нулю волновым вектором: q → 0, что в контексте данного теоретического подхода означает: q2$ \ll $ |gµBB|Mx (ср. с уравнением (7)). При этом сохраняется компонента Sz, и тем самым зеемановская энергия, но меняется полный спин: S → S – 1. Таким образом, при макроскопическом рассмотрении спиновой системы как единого целого мы должны в правую часть уравнения (1) подставить член (4). В компонентах оно приобретает вид:
(8)
${{\partial {{{\vec {S}}}_{ \bot }}} \mathord{\left/ {\vphantom {{\partial {{{\vec {S}}}_{ \bot }}} {\partial t}}} \right. \kern-0em} {\partial t}} = --g{{\mu }_{B}}{{\vec {S}}_{ \bot }} \times ~\vec {B}--{{{{{\vec {S}}}_{ \bot }}} \mathord{\left/ {\vphantom {{{{{\vec {S}}}_{ \bot }}} {{{T}_{2}}}}} \right. \kern-0em} {{{T}_{2}}}};\,\,\,{{\partial {{S}_{z}}} \mathord{\left/ {\vphantom {{\partial {{S}_{z}}} {\partial t}}} \right. \kern-0em} {\partial t}} = 0,$С другой стороны, подобный подход и уравнение (8) не применимы при полном отсутствии спиновой жесткости, т.е. при полном пренебрежении кулоновским взаимодействием электронов. В этом случае спины электронов совершают в магнитном поле независимое прецессионное движение, которое, однако, вполне синхронно, если магнитный беспорядок пренебрежимо мал. С течением времени влияние магнитного беспорядка будет проявляться все сильнее, так как даже ничтожное различие зеемановских частот |g($\vec {r}$)µBB|/$\hbar $ в разных точках $\vec {r}$ двумерного пространства будет приводить к нарастанию расфазировки прецессионного движения, а в конечном счете и к полной расфазировке, т.е. к обращению компоненты ${{\vec {S}}_{ \bot }}(t)$ в ноль. Физически очевидно также, что спиновая жесткость будет препятствовать расфазировке, причем это сопротивление расфазировке будет усиливаться по мере ее нарастания. При отсутствии же расфазировки синхронная прецессия полного спина ансамбля невзаимодействующих электронов ничем неотличима от прецессии спина в ферромагнетике, и спиновая жесткость, определяемая электрон-электронным взаимодействием, тогда не играет никакой роли.
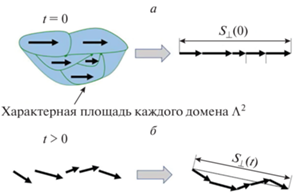
В первую очередь мы рассмотрим самую начальную стадию прецессии при очень малых временах t, когда расфазировка настолько мала, что спиновой жесткостью мы вообще пренебрежем. Задача при этом превращается из динамической в геометрически-кинематическую. Пусть в момент t = 0 система является макроскопически полностью спин-поляризованной. При этом полная макроскопическая поляризация подразумевает то, что суммарный спиновый момент всякого 2D-домена с размерами, большими магнитной длины (характерного масштаба одноэлектронной волновой функции), в любой точке 2D пространства направлен одинаково, хотя это отнюдь не означает, что все электроны системы квантово-механически находятся в одном и том же спиновом состоянии (cм. по этому поводу работу [18]). Итак мы представим картину так, что полный поперечный спин ${{\vec {S}}_{ \bot }}(0)$ складывается из поперечных компонент спиновых моментов отдельных 2D-доменов, которые параллельны и сонаправлены (см. рис. 3а). Будем также считать, что линейный размер этих доменов имеет масштаб корреляционной длины пространственных магнитных флуктуаций Λ (например, флуктуаций g-фактора), которая, разумеется, намного больше магнитной длины lB. Затем, поскольку в различных доменах отличаются зеемановские энергии |g(${{\vec {r}}_{i}}$)µBB| (i – номер домена), то домены прецессируют с разными частотами. Их сонаправленность таким образом нарушается, а полный поперечный спин ${{\vec {S}}_{ \bot }}(t)$ станет меньше по модулю чем первоначальная величина ${{\vec {S}}_{ \bot }}(0)$ см. рис. 3б. Наша задача оценить разность
Рис. 3.
В момент времени t = 0 поперечные спиновые моменты всех доменов сонаправлены (см. текст) и складываются в полный поперечный момент S⊥(0) (а). При t > 0 вследствие расфазировки прецессии поперечные моменты доменов “расходятся” по направлениям и полный поперечный момент S⊥(t) становится по величине меньше: S⊥(t) < S⊥(0) (б).
предполагая при этом, что эта величина мала: ∆S $ \ll $ S⊥(0). Пусть A площадь системы, а Ai и ${{\vec {n}}_{i}}(t)$ соответственно площадь домена и двумерный единичный вектор в направлении поперечной составляющей спина домена (разумеется, A = ΣiAi). Тогда S⊥(t) = S⊥(0)|ΣIAi${{\vec {n}}_{i}}$(t)|/A. Азимутальный угол ϕi для каждого из векторов ${{\vec {n}}_{i}}$ = (cosϕi, sinϕi) удобно отсчитывать от их общего среднего направления, задаваемого углом ϕ0(t) = |g0µBB|t/ħ, где g0= = 〈g〉r – усредненное в пространстве значение. То есть эффективный g-фактор представляется в виде g = g0+ g'($\vec {r}$), причем для пространственно-флуктуирующей части имеем 〈g'〉r = 0. Все углы
(10)
${{\phi }_{i}}(t) = \left| {g_{i}^{'}{{\mu }_{B}}B} \right|{t \mathord{\left/ {\vphantom {t \hbar }} \right. \kern-0em} \hbar }$(здесь $g_{i}^{'}$ = g'(${{\vec {r}}_{i}}$)) на начальной стадии расфазировки малы, и, кроме того, для оценки достаточно считать, что все Ai одинаковы: Ai = A/N (N общее число доменов; N ∼ A/Λ2$ \gg $ 1). Тогда после простых манипуляций получим величину изменения поперечного спина (9):
(11)
${{\Delta }_{S}}(t) \sim ({{{{S}_{ \bot }}(0)} \mathord{\left/ {\vphantom {{{{S}_{ \bot }}(0)} {2{{N}^{2}}}}} \right. \kern-0em} {2{{N}^{2}}}}){{\Sigma }_{{i,j}}}{{({{\phi }_{i}}--{{\phi }_{j}})}^{2}}.$Теперь, используя (10), остается только оценить величину
(12)
${{\Sigma }_{{i,j}}}{{(g_{i}^{'}--g_{i}^{'})}^{2}} \equiv \,\,2{{\Sigma }_{{i,j}}}~g_{i}^{{'2}}--{{\Sigma }_{{i \ne j}}}~g_{i}^{'}g_{j}^{'}.$Первая из сумм здесь в правой части пропорциональна N2. Если характерная амплитуда пространственных флуктуаций g-фактора равна ∆g, то оценка для этой суммы $ \sim {\kern 1pt} {{N}^{2}}\Delta _{g}^{2}.$ Вторая же сумма гораздо меньше. Она оказывается пропорциональной N, в силу того что корреляционная длина Λ много меньше, чем размер системы $\sqrt A $ и корреляции между g-факторами удаленных друг от друга доменов (когда |${{\vec {r}}_{i}}$ – ${{\vec {r}}_{j}}$| $ \gg $ Λ) отсутствуют. Наконец, в соответствии с формулой (9) мы находим в результате, что на начальной стадии, когда спиновой жесткостью можно пренебречь, затухание прецессии определяется квадратичной зависимостью:
(13)
$\Delta {{S}_{ \bot }}(t) \sim {{S}_{ \bot }}(0){{\left( {{t \mathord{\left/ {\vphantom {t {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}}} \right)}^{2}},\,\,\,{\text{где}}\,\,\,\tau _{0}^{{ - 1}} = {{{{\mu }_{B}}B{{\Delta }_{g}}} \mathord{\left/ {\vphantom {{{{\mu }_{B}}B{{\Delta }_{g}}} \hbar }} \right. \kern-0em} \hbar }.$Разумеется, эта оценка годится только для малых времен, t $ \ll $ τ0. Отметим, что величина τ0 зависит от амплитуды ∆g, т.е. определяется величиной разброса прецессионных частот, но не зависит от корреляционной длины Λ. Иными словами, не зависит от конкретного распределения g($\vec {r}$) в 2D пространстве. Такой результат совершенно ожидаем для одноэлектронной задачи, в которой орбитальное состояние электрона на уровне Ландау не определено и совершенно произвольно.
Возникает вопрос: начиная с какого времени t, необходимо учитывать спиновую жесткость? Ведь в результате, как это следует из уравнения (8), закон изменения поперечного спина должен стать другим и со временем, но все еще при малых отклонениях спина от начального значения, он будет линейным:
(14)
$\Delta {{S}_{ \bot }}(t) \sim {{{{S}_{ \bot }}(0)t} \mathord{\left/ {\vphantom {{{{S}_{ \bot }}(0)t} {{{T}_{2}}\,\,\,}}} \right. \kern-0em} {{{T}_{2}}\,\,\,}}(t \ll {{T}_{2}}).$Очевидно, существует некоторое характерное время τtr такое что при t ∼ τtr происходит переход от квадратичного закона к линейному (14). Фактически, эта задача может быть решена только микроскопически, но и тут возможны общие феноменологические соображения, которые позволяют сделать правильные оценки. Как уже говорилось, элементарный процесс поперечной релаксации (S → S – 1 при Sz = const) представляет собой превращение голдстоуновского спинового экситона, имеющего энергию, равную зеемановской |gµBB|, в спин-волновой экситон. Второе слагаемое в правой части уравнения (6) представляет собой обменную энергию, которая возникает при $\vec {q}$ ≠ 0, т.е. при нарушении трансляционной симметрии системы. В данном случае трансляционная симметрия нарушается из-за пространственной неоднородности g-фактора. Оператор зеемановской энергии
(15)
${{V}_{g}} = ({{{{\mu }_{B}}B} \mathord{\left/ {\vphantom {{{{\mu }_{B}}B} 2}} \right. \kern-0em} 2}){{\Sigma }_{n}}g'({{\vec {r}}_{n}}){{\sigma }_{{zn}}}$(здесь индекс n нумерует электроны, σzn – матрица Паули) смешивает спиновые и пространственные переменные, так что вследствие расфазировки спиновой прецессии появляется квантовые флуктуации обменной энергии порядка $ \sim {\kern 1pt} {{l_{B}^{2}} \mathord{\left/ {\vphantom {{l_{B}^{2}} {{{M}_{x}}{{\Lambda }^{2}}}}} \right. \kern-0em} {{{M}_{x}}{{\Lambda }^{2}}}}$ (учтено, что q ∼ lB/Λ – эффективная величина флуктуаций в K-пространстве с учетом обезразмеривания). Характерное время развития этих флуктуаций равно τtr ∼ Mx(Λ/lB)2, что соответствует вкладу порядка единицы в фазу многоэлектронной волновой функции системы. Естественно, предполагать, что, начиная с этих времен, уже нельзя игнорировать спиновую жесткость и квадратичная стадия поперечной релаксации прекращается. Переходное время τtr оказывается больше периода спиновой прецессии ℏ/g0µBB ∼ 0.01 нc, но в то же время намного короче найденного выше времени τ0 ∼ 1 нс (реальные оценки даны в работах [13] и [18]). Поэтому для квадратичного закона (13) требуется выполнение условия t < τtr, существенно более жесткого чем t < τ0. Наконец, оценим время поперечной релаксации T2. Чтобы его найти необходимо решать микроскопическую задачу в рамках пертурбативного подхода для нестационарной многоэлектронной волновой функции, где возмущением является флуктуирующая в пространстве зеемановская энергия, определяемая оператором (15). В то же время уже из соображений размерности можно оценить величину T2. Располагая двумя, имеющими физическое значение характеристиками τ0 и τtr, легко видеть, что простейший вид третьей, имеющей размерность времени и обладающей искомыми свойствами (например, пропорциональностью спиновой жесткости, ∝ $M_{x}^{{ - 1}}$), будет таким
(16)
${{T}_{2}} = {{\tau _{0}^{2}} \mathord{\left/ {\vphantom {{\tau _{0}^{2}} {{{\tau }_{{tr}}}}}} \right. \kern-0em} {{{\tau }_{{tr}}}}} \sim \frac{{\hbar l_{B}^{2}}}{{{{M}_{x}}~{{{\left( {{{{{\Delta }}}_{g}}{{{{\mu }}}_{B}}B{{\Lambda }}} \right)}}^{2}}}}.$Если считать, что Mx ∝ lB, то получим T2 ∝ B–5/2 при условии, что в системе фиксирован фактор заполнения ν. Можно оценить, что при ν = 1 и B = 5 Tл время T2 должно быть порядка 10 нс. Это вполне соответствует экспериментальным данным [12–14].
До сих пор в качестве магнитного беспорядка мы рассматривали пространственные флуктуации g-фактора. В заключение коснемся другого типа беспорядка, а именно, связанного со сверхтонким взаимодействием электронов с ядрами. В процессе лазерного возбуждения спиновой голдстоуновской моды могут возникнуть длинноволновые флуктуации намагниченности ядер Ga и As. Изучение этого явления на основе эксперимента [14] показывает, что задача о поперечной спиновой релаксации остается примерно такой же, только пространственные флуктуации зеемановской энергии будут вместо амплитуды ∆gµBB определяться величиной AGaAsΔm, где AGaAs ∼ 1K – некоторый параметр, связанный с константой сверхтонкого взаимодействия электронов с ядрами (см. [19]), а Δm ∼ 0.01 – амплитуда длинноволновых флуктуаций компоненты среднего спина ядер, направленной вдоль поля $\vec {B}.$ При этом корреляционная длина флуктуаций намагниченности ядер оценочно больше, чем корреляционная длина при флуктуациях g-фактора, а именно: Λ/lB ∼ 30, т.к. она определяется теперь длиной световой волны лазера. В результате получим
(17)
${{T}_{2}} \sim \frac{{\hbar l_{B}^{2}}}{{{{M}_{x}}~{{{\left( {{{\Delta }_{m}}{{A}_{{GaAs}}}\Lambda } \right)}}^{2}}}},$что тоже составит ∼10 нс, но переходное время, τtr = ℏMx(Λ/lB)2, при этом оказывается на порядок больше, чем в предыдущем случае. В результате линейная стадия поперечной релаксации может фактически не проявиться. Кроме того, релаксация, связанная с намагниченностью ядер, должна быть зависимой от температуры: c увеличением последней до величин $ \gtrsim {\kern 1pt} 10$ K амплитуда ∆m, по-видимому, cущественно падает, т.е. время (17) растет и затухание керровских осцилляций замедляется.
Работа выполнена в рамках темы государственного задания ИФТТ РАН.
Список литературы
Pinczuk A., Dennis B.S., Heiman D. et al. // Phys. Rev. Lett. 1992. V. 68. No. 24. P. 3622.
Pinczuk A., Dennis B.S., Pfeiffer L.N., West K. // Phys. Rev. Lett. 1993. V. 70. No. 25. P. 3983.
Gallais Y., Yan J., Pinczuk A. et al. // Phys. Rev. Lett. 2004. V. 100. No. 8. Art. No. 086806.
Kukushkin I.V., Smet J.H., Scarola V.W. et al. // Science. 2009. V. 324. No. 5930. P. 1044.
Drozdov I.K., Kulik L.V., Zhuravlev A.S. et al. // Phys. Rev. Lett. 2010. V. 104. No. 13. Art. No. 136804.
Barret S.E., Dabbagh G., Pfeiffer L.N. et al. // Phys. Rev. Lett. 1995. V. 74. No. 25. P. 5112.
Bayot V., Grivei E., Melinte S. et al. // Phys. Rev. Lett. 1996. V. 76. No. 24. P. 4584.
Schmeller A., Eisenstein J.P., Pfeiffer L.N., West K.W. // Phys. Rev. Lett. 1995. V. 75. No. 23. P. 4290.
Maryenko D., Falson J., Kozuka Y. et al. // Phys. Rev. B. 2014. V. 90. No. 24. Art. No. 245303.
Falson J., Maryenko D., Friess B. et al. // Nature Phys. 2015. V. 11. P. 347.
Ваньков А.Б., Кайсин Б.Д., Кукушкин И.В. // Письма в ЖЭТФ. 2018. Т. 107. № 2. С. 110; Van’kov A.B., Kaysin B.D., Kukushkin I.V. // JETP Lett. 2018. V. 107. No. 2. P. 106.
Fukuoka D., Oto K., Muro K. et al. // Phys. Rev. Lett. 2010. V. 105. No. 12. Art. No. 126802.
Larionov A.V., Kulik L.V., Dickmann S., Kukushkin I.V. // Phys. Rev. B. 2015. V. 92. No. 16. Art. No. 165417.
Larionov A.V., Stepanets-Khussein E., Kulik L.V. et al. // Sci. Rep. 2020. V. 10. P. 2270.
Laughlin R.B. // Phys. Rev. Lett. 1983. V. 50. No. 18. P. 1395.
Бычков Ю.А., Иорданский С.В., Элиашберг Г.М. // Письма в ЖЭТФ. 1981. Т. 33. № 3. С. 152; Bychkov Yu.A., Iordanskii S.V., Eliashberg G.M. // JETP Lett. 1981. V. 33. No. 3. P. 143.
Kallin C., Halperin B.I. // Phys. Rev. B. 1984. V. 30. No. 10. P. 5655.
Dickmann S. // J. Phys. Cond. Matter. 2020. V. 32. No. 1. Art. No. 015603.
Dickmann S. // J. Phys. Cond. Matter. 2021. V. 33. No. 10. Art. No. 105602.
Landau L.D., Lifshitz E.M. // Phys. Z. Sowietunion. 1935. V. 8. P. 153.
Dickmann S. // Phys. Rev. Lett. 2004. V. 93. No. 20. Art. No. 206804.
Dickmann S. // Письма в ЖЭТФ. 2011. Т. 93. № 2. С. 88; Dickmann S. // JETP Lett. 2011. V. 93. No. 2. P. 86.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


