Известия РАН. Серия физическая, 2022, T. 86, № 5, стр. 692-696

ВВЕДЕНИЕ

Первоначально в [1] был проиллюстрирован способ создания метаматериала в радиочастотном диапазоне. Отметим, что в качестве ячейки метаматериала рассматриваются два параллельно расположенных элемента, один из которых – диэлектрик, а второй – последовательно-периодически соединенные между собой нечетные однопроводные открытые линии связи. Далее с использованием данных элементов создается многослойная метаструктура. Этот метод создания левосторонних материалов (left handed materials, LHM) [2] не является резонансным. Он широкополосный и перспективен для применения к антенной технике, чем возможный второй способ реализации метаматериала в виде метаструктуры с размерами ячейки много меньше длины волны передающего сигнала, содержащей тонкие проводящие стержни и разомкнутые рамки [3, 4].

В последнее время перспективными метаматериалами, помимо гиперболоидных [5–7] и магнитооптических композитных метаматериалов [8], являются боратные стекла с парамагнитными добавками – ионами Сu¹⁺, Сu²⁺, Fe²⁺, Fe³⁺ и другие [8, 9]. Калиево-алюмоборатные (КАБ) стекла, активированные ионами Fe³⁺ [9–12] имеют ярко выраженные особенности радиационно-оптических и терморадиационных свойств. Несмотря на то, что радиационно-оптические свойства достаточно изучены, существуют своеобразные превращения парамагнитных радиационно-наведенных центров окраски в кислородсодержащей среде вида BO₃ и BO₄ (3-х и 4-х координированный бор, соответственно). Они возникают под воздействием рентгеновского и гамма-излучения ⁶⁰Co, а также высоких температур. Радиационно-наведенными центрами окраски являются $\left[ {{\text{B}}{{{\text{o}}}_{3}}} \right]_{i}^{{e - }}$ и $\left[ {{\text{B}}{{{\text{o}}}_{4}}} \right]_{i}^{{e + }}$ – соответственно электронные и дырочные центры окраски в боратных стеклах, взаимодействующие и составляющие комплексоны вида $\left\{ {{{\left[ {{\text{B}}{{{\text{o}}}_{3}}} \right]_{i}^{{e - }}} \mathord{\left/ {\vphantom {{\left[ {{\text{B}}{{{\text{o}}}_{3}}} \right]_{i}^{{e - }}} {{\text{F}}{{{\text{e}}}^{{3 + }}}}}} \right. \kern-0em} {{\text{F}}{{{\text{e}}}^{{3 + }}}}}} \right\},$ $\left\{ {{{\left[ {{\text{B}}{{{\text{o}}}_{{\text{4}}}}} \right]_{i}^{{e + }}} \mathord{\left/ {\vphantom {{\left[ {{\text{B}}{{{\text{o}}}_{{\text{4}}}}} \right]_{i}^{{e + }}} {{\text{F}}{{{\text{e}}}^{{{\text{3 + }}}}}}}} \right. \kern-0em} {{\text{F}}{{{\text{e}}}^{{{\text{3 + }}}}}}}} \right\}$ и другие комплексоны с ионами Сu¹⁺, Сu²⁺. Совместное влияние термического и радиационных полей [10–12] приводит к изменению координационного состояния ионов-активаторов в среде. При этом наблюдается отрицательное дифференциальное поглощение ∆D < 0, которое приводит к тому, что у среды появляется отрицательный коэффициент рефракции ∆n < 0. В этом достаточно легко убедиться по результатам работы [11] (см. рис. 2 в указанной работе). Впервые отрицательное дифференциальное поглощение в спектрах боратных стекол с оксидами железа было показано в работе [13].

Состояние ионов железа Fe²⁺, Fe³⁺ рассматривается как парамагнитный зонд, с помощью которого выявляется отрицательное ЭПР поглощение по отношению к исходным стеклам. Показано, что отрицательное радиационное наведенное поглощение в терморадиационных поглощениях свидетельствует о гомогенизации структуры стекла и позволяет получить новые материалы из кислородосодержащих стекла без оптических потерь.

В работах [14, 15] явление отрицательного дифференциального поглощения связывалось с отрицательным индексом поглощения или отрицательным коэффициентом рефракции, что непосредственно сказывается на проявление свойств метаматериала в калиево-алюмоборатных стеклах с добавками ионов железа Fe³⁺ при терморадиационных воздействиях.

Авторы [14, 15] предполагают, что

где n₀ – постоянный показатель преломления, δn_E/n₀ – относительный показатель преломления, учитывающий дисперсию. Заменяя, для простоты α_m(E) = α; n_E = n_~ и, учитывая (1) для производной [dα_~/dn_~], находим:

Для простоты обозначим (n_∼/n₀) = $n_{ \sim }^{'}$ и окончательно получим

Для метаматериала можно принять –1 < $n_{ \sim }^{'}$ < < +1 и вычисление по (3) показывает, что –4 < < Δα_~ < –2.25. Таким образом, отрицательное значение коэффициента поглощения, обусловленное терморадиационным воздействием, приводит к отрицательному значению индекса преломления оксидного стекла. Физически это означает, что при определенных условиях эксперимента стекло становится самопрозрачным.

В настоящей работе в отличии от [1] предлагается метод изучения правосторонних (right handed materials, RHM) и LHM материалов с целью создания метаматериалов в оптическом диапазоне аналогично радиодиапазону [16]. При расчетах мы пользуемся компьютерными программами, описанными в [17, 18]. Далее, рассматривая эквивалентную схему системы связи с распределенными параметрами [1], с учетом ограничения линейных пространственных размеров, получаем, что в метаматериале, который находится между передатчиком и приемником распространяются, как бегущие, так и отраженные волны, аналогичные СВЧ диапазону.

РАСЧЕТ СИСТЕМЫ ПЕРЕДАЧИ СИГНАЛА ПО ВОЛНОВОМУ АНАЛОГУ ДЛЯ RHM МАТЕРИАЛА

Для простоты расчетов рассмотрим плоскую скалярную монохроматическую волну вида

Если в (1) учесть оба члена, то можно рассмотреть нелинейные процессы. Учет только второго члена (1) приведет к рассмотрению лишь линейных процессов. В этом случае необходимо добавить комплексно-сопряженный член.

Можно показать [16], что в прямоугольной системе координат составляющие волнового вектора будут следующими:

где угол α выбран между $\vec {k}$ и плоскостью OYZ, φ – между ${{k}_{z}}$ и проекцией $\vec {k}$ на плоскость OYZ. Из (5) следует, что независимыми угловыми переменными являются только две ${{k}_{x}} = {{u}_{1}};$ ${{k}_{y}} = {{u}_{2}}.$

В таком случае общим решением волнового уравнения с учетом (4) является $P = p(x,y,z){{e}^{{ - i\omega t}}},$ где

Для распростронения плоской волны в свободном пространстве начиная от плоскости раскроя передающей антенны должно выполнятся следующее условие $u_{1}^{2} + u_{2}^{2} \leqslant {{k}^{2}}.$

Поскольку электромагнитное поле в виде плоской волны (4)–(6) с разными параметрами является решением волнового уравнения, то решение будет получено в виде суммы (интеграла) полей вида (7) для трехмерной системы:

где g(u₁, u₂) комплексная функция, описывающая амплитуду и фазу отдельной плоской волны с направлением распространения, определяющая совокупностью действительных переменных u₁, u₂, т.е. все возможные плоские волны, в том числе неоднородные.

Уравнение (7) является обобщением решения волнового уравнения на случай неплоской монохроматической волны, например для сферической волны. От (7) можно перейти к реальному полю, если умножить его на exp(–jωt) и прибавить к комплексно-сопряженный член.

Пусть даны значения волнового уравнения на плоскости z = 0 (начальная плоскость расположения антенны) диаграммы направленности. Требуется найти решение волнового уравнения, превращающееся в заданную функцию на плоскости z = 0. Из условий излучения Кирхгоффа на бесконечной сфере волнового поля эта функция должна быть равна нулю. Из (7) получим следующее

где

Определив спектр частот g(u₁, u₂) из (9) и p(x, y, 0, t), находим граничные условия при z = 0.

Из (8), (9) вытекает, что для неоднородных бегущих волн $u_{1}^{2} + u_{2}^{2} > {{k}^{2}},$ причем из (7) можно выделить решение p(x,y,z) при z > 0 (неоднородные бегущие волны) и при z < 0, соответствующее обратным волнам.

В частном случае (8) и (9) при z = 0, y = 0 находим пространственное распределение полей для одномерного (1D) случая:

Формула (10) справедлива при любом значении z. Координаты точек пространства x, y имеют размерность длины l. Переменные u₁, u₂ имеют размерность обратной длины волны см^–1 и соответствуют пространственным частотам. Формулы (8) и (9) соответствуют двумерным (2D) интегралам Фурье; формулы (10), (11) соответствуют обычным 1D интегралам Фурье. Используем их для расчета системы передачи сигнала по волновому каналу. Для получения пространственного спектра сигнала используем явный вид входной функции f(x, z_x = 0). В данном случае возьмем в качестве нее спектральную зависимость КАБ стекла [10]. Спектр поглощения для отдельного центра окраски имеет гауссову форму:

где, $\Delta \omega _{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{\text{Г}}} = \frac{1}{{2\sqrt {\ln 2} }}{{\delta }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – полуширина на полувысоте, ${{\delta }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – параметр, ω₀ – резонансная частота.

С учетом (12) формула (6) для “пространственной частоты” приобретает следующий вид

где для простоты вычислений в случае RHM материала приняты следующие обозначения:

После преобразований и вычислений с использованием теории вычетов [19, 20], получим

где для применения теории вычетов проведена замена переменных $u{\kern 1pt} ' = {\text{tg}}\left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-0em} 2}} \right)$ [19, 20], в таком случае выражение $\cos \left( {b{{\omega }_{0}}\omega u{\kern 1pt} '} \right)$ при ${{\omega }_{0}} = 1$ будет равно $\cos \left( {\frac{{{{\omega }^{2}}}}{{\delta {{\omega }^{2}}}}} \right).$ Тогда из (16) получим окончательную формулу где через $\varphi \left( {{{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} {2{{\omega }_{0}}}}} \right. \kern-0em} {2{{\omega }_{0}}}}} \right)$ обозначено $\exp \left( {{{{{\tau }^{2}}} \mathord{\left/ {\vphantom {{{{\tau }^{2}}} 2}} \right. \kern-0em} 2}} \right),$ здесь $\tau = u\omega ,$ другими словами за единицу измерений можно принять ${{\omega }_{0}} = 1,$ в свою очередь $\exp \left( {{{{{\tau }^{2}}} \mathord{\left/ {\vphantom {{{{\tau }^{2}}} 2}} \right. \kern-0em} 2}} \right)$ является табулированной функцией [20].

РАСЧЕТ СИСТЕМЫ ПЕРЕДАЧИ СИГНАЛА ПО ВОЛНОВОМУ КАНАЛУ С УЧЕТОМ ПРИСУТСТВИЯ LHM МАТЕРИАЛА

По аналогии с предыдущим пунктом были проведены расчеты для LHM материала, которые для III-квадранта (ε(ω) < 0, µ(ω) < 0), привели к следующему результату:

где переменная u с одной стороны, имеет смысл “пространственных частот”, и по размерности соответствует обратной длине волны, а с другой стороны, – это параметр распространения плоских волн.

Для среды с LHM метаматериалом, аналогично (15), (16), проводя замену переменных и применяя теорию вычетов, после всех преобразований получаем следующую формулу:

Отметим, что получена также формула для метаматериала с отрицательным коэффициентом поглощения по пространственному распределению амплитуды полей в виде

Проблема размерностей при вычислениях табулированной функции учтена в формулах (17) и (20), за счет замены переменных [19, 20].

РЕЗУЛЬТАТЫ РАСЧЕТОВ И ИХ ОБСУЖДЕНИЕ

Следуя (10)–(16), рассчитываем отношение пространственных спектров частот

Результаты расчетов по формуле (21) представлены в виде графика на рис. 1.

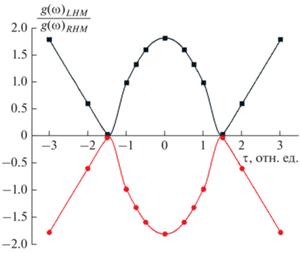
Важно отметить, что в направлении распространения “бегущих волн” (u = 1) наблюдается пространственный спектр (рис. 1) с поглощением бегущих волн в диапазоне частот τ = ω/ω₀ = 1–2, а при 2 < ω/ω₀ < 4 наблюдается усиление гармоник.

Заметим, что вычисления при k = u = –1 (рис. 1, красная линия) в зависимости от ω/ω₀ аналогичны и при k = +1 (рис. 1, черная линия). Используя (13) и (16), получим важную формулу, характеризующую распределение амплитуды электромагнитного поля в среде с LHM метаматериалом по отношению к обычным (RHM) материалам:

Сопоставление результатов настоящей работы с данными из [6–9] показывает, что данная амплитудно-частотная характеристика (рис. 2) является широкополосной и явно заметно усиление сигнала средой метаматериалов.

Распределение амплитуд (22) от относительной частоты представлено на рис. 2. Видно, что во всем диапазоне рабочих частот наблюдается усиление сигнала, а также широкополосность системы с метаматериалом.

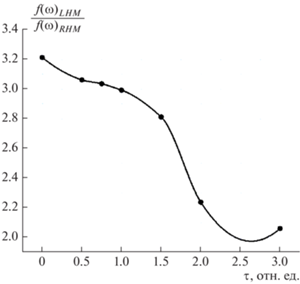
Отметим также, что реально создаются, как последовательное соединенные, так и параллельно расположенные элементы [1, 21], что позволяет обеспечивать значительное усиление по сравнению с обсужденной однонаправленной линейной системой.

ЗАКЛЮЧЕНИЕ

Результатом исследования является теоретическое решение задачи получения метаматериала из аморфного стекла. Для обеспечения необходимых показателей метаматериала при радиационной обработке, с учетом высоких температур облучения перспективно рассматривать аморфные пленки из магнитооптического КАБ стекла с добавками оксида железа.

По аналогии отрицательного дифференциального поглощения центров окраски (в КАБ – стеклах с добавками Fe₂O₃) и мощности передачи сигнала в метаматериале получена связь отрицательного коэффициента рефракции с отрицательным дифференциальным поглощением центров окраски при терморадиационном воздействии.

Представлены расчеты системы передачи сигнала для правосторонних и левосторонних материалов. Получены численные значения коэффициента усиления при разных значениях частоты для среды с метаматериалом. Результаты расчета показывают возможность преобразования сигнала на основе метаматериала как в радиочастотном, так и в оптическом диапазоне волн.