Известия РАН. Серия физическая, 2022, T. 86, № 5, стр. 753-757

Влияние магнитной анизотропии на динамику колебаний вектора намагниченности в магнитных пленках

В. Н. Шапоров^1, *, Л. Н. Котов¹, В. С. Власов¹

¹ Федеральное государственное бюджетное образовательное учреждение высшего образования “Сыктывкарский государственный университет имени Питирима Сорокина”
Сыктывкар, Россия

^* E-mail: shaporov@mail.ru

Поступила в редакцию 13.12.2021
После доработки 24.12.2021
Принята к публикации 21.01.2022

EDN: YBVNMQ
DOI: 10.31857/S0367676522050234

Полный текст (PDF)

Аннотация

Изучено влияние магнитной анизотропии на временные, частотные и полевые зависимости колебаний вектора намагниченности в магнитных пленках, возникающих под действием переменного магнитного поля. Показано, что при наличии магнитной анизотропии, переориентация вектора намагниченности в пленках между двумя взаимно перпендикулярными осями легкого намагничивания, может сопровождаться нелинейными колебаниями с наличием бифуркаций.

ВВЕДЕНИЕ

Железоиттриевый гранат удобно использовать для моделирования физических процессов, поскольку его параметры широко известны, и имеют самую узкую ширину линии ферромагнитного резонанса среди магнетиков, и, соответственно, малые магнитные потери. Кроме того, значение полей анизотропии в железоиттриевом гранате такие, что позволяют при относительно небольшом по амплитуде переменным полем, переориентировать вектор намагниченности с одной оси легкого намагничивания на другую, особенно когда одна из осей легкого намагничивания перпендикулярна плоскости пленок. При перпендикулярной ориентации вектора намагниченности к плоскости пленки изменения температуры и внутренние напряжения существенно меньше влияют на его динамику [1], поэтому ими можно пренебречь при расчетах. В железоиттриевом гранате при изменении температуры первая ${{K}_{1}}$ и вторая ${{K}_{2}}$ константы магнитной кристаллической анизотропии могут изменяться в широких пределах, что позволяет сильно менять магнитную динамику колебаний. В настоящей работе исследованы режимы колебаний вектора намагниченности в магнитных пленках с наличием и отсутствием магнитной кристаллической анизотропии.

ОПИСАНИЕ УРАВНЕНИЙ МАГНИТНОЙ ДИНАМИКИ

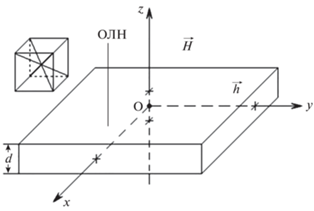
Для расчетов амплитуд колебаний вектора намагниченности, возникающих под действием переменного магнитного поля, были взяты параметры и характеристики железоиттриевого граната. При решении уравнений считалось, что одна из кристаллографических осей легкого намагничивания перпендикулярна к плоскости пленки. Внешнее постоянное магнитное поле также направлено перпендикулярно плоскости, а переменное поле имеет круговую поляризацию, при этом плоскость вращения вектора переменного поля совпадает с плоскостью пленки. Декартова система координат выбрана так, что ось z, кристаллографическая ось [001], и постоянное магнитное поле $\vec {H}$ перпендикулярны к плоскости пленки (рис. 1).

Рис. 1.

Геометрия векторов постоянного $\vec {H}$ и переменного $\vec {h}$ магнитных полей и оси легкого намагничивания пленки (ОЛН).

Компоненты и ориентация вектора намагниченности в пленке определялись из решения уравнения Ландау–Лифшица, в котором затухание магнитных колебаний учитывалось с помощью релаксационного члена в форме Гильберта [2, 3]

(1)

$\frac{{\partial{ \vec {m}}}}{{\partial t}} = - {{\gamma }}\left[ {\vec {m} \times {{{\vec {H}}}_{e}}} \right] + {{\alpha }}\left[ {\vec {m} \times \frac{{\partial{ \vec {m}}}}{{\partial t}}} \right]~,$

где ${{\vec {H}}_{e}}$ – эффективное магнитное поле, действующее на вектор намагниченности, $\vec {m}$ – единичный вектор намагниченности пленки, ${{\gamma }}$ – гиромагнитное отношение материала пленки, ${{\alpha }}$ – параметр магнитной диссипации. Энергия ферромагнетика $U$ включает в себя энергию внешнего поля ${{U}_{Z}},$ энергию размагничивающего поля ${{U}_{d}}~$ и энергию магнитной анизотропии пленки ${{U}_{a}}$:

(2)

$U = {{U}_{Z}} + {{U}_{d}} + {{U}_{a}}.$

Энергия ${{U}_{Z}}$ вектора намагниченности $\vec {M}$ во внешнем поле $\vec {H},$ энергия ${{U}_{d}}~$ для тонкой пленки, в выбранной системе координат, определялись выражениями:

(3)

${{U}_{Z}} = - \vec {M} \cdot {{\vec {H}}_{{ex}}} = - {{M}_{s}}\vec {m} \cdot \left( {\vec {H} + {{{\vec {h}}}_{\sim }}} \right)~,$

(4)

$\begin{gathered} {{U}_{d}} = - \frac{1}{2}~\vec {M} \cdot {{{\vec {H}}}_{d}} = \\ = \,\, - \frac{1}{2}~{{M}_{s}}\vec {m} \cdot \left( { - 4{{\pi }}{{M}_{s}}\vec {m}\hat {N}} \right) = 2{{\pi }}M_{s}^{2}m_{z}^{2}, \\ \end{gathered} $

(5)

$\hat {N} = \left( {\begin{array}{*{20}{c}} 0&0&0 \\ 0&0&0 \\ 0&0&1 \end{array}} \right)~,$

где ${{M}_{s}}$ – намагниченность насыщения, ${{\vec {H}}_{{ex}}}$ – внешнее магнитное поле, ${{\vec {H}}_{d}}$ – размагничивающее поле, $\hat {N}$ – тензор размагничивающих коэффициентов для перпендикулярно намагниченной тонкой пленки [4], ${{m}_{z}}$ – проекция единичного вектора намагниченности на ось z, $\vec {H}$ – внешнее постоянное магнитное поле (перпендикулярно плоскости пленки), ${{\vec {h}}_{\sim }}$ – внешнее переменное магнитное поле (лежит в плоскости пленки). Для магнитных кубических кристаллов плотность энергии магнитной анизотропии выбиралась в следующем виде [2]:

(6)

${{U}_{a}} = {{K}_{1}}\left( {m_{x}^{2}m_{y}^{2} + m_{x}^{2}m_{z}^{2} + m_{y}^{2}m_{z}^{2}} \right) + {{K}_{2}}\left( {m_{x}^{2}m_{y}^{2}m_{z}^{2}} \right)~.$

Минимизация энергии магнитной анизотропии (6) показывает, что в магнитном кубическом кристалле есть шесть направлений, соответствующих осям легкого намагничивания, четыре из которых параллельны плоскости пленки [3]. Проекции эффективного поля ${{\vec {H}}_{e}}$ на оси координат можно найти из выражения для полной энергии магнетика во внешних магнитных полях

(7)

${{H}_{{ek}}} = - \frac{1}{{{{M}_{s}}}}\frac{{\partial U}}{{\partial {{m}_{k}}}},\,\,\,\,k = \left\{ {x,y,z} \right\}~,$

где ${{H}_{{ek}}},$ ${{m}_{k}}$ – проекции вектора эффективного поля и единичного вектора намагниченности на координатные оси. Подставляя (2)–(6) в (7), получим выражения для компонент эффективного поля

(8)

$\begin{gathered} {{H}_{{ex}}} = {{h}_{x}}\left( t \right) + {{H}_{{ax}}},\,\,\,\,{{H}_{{ey}}} = {{h}_{y}}\left( t \right) + {{H}_{{ay}}}, \\ {{H}_{{ez}}} = H - 4{{\pi }}{{M}_{s}}{{m}_{z}} + {{H}_{{az}}}, \\ \end{gathered} $

где ${{H}_{{ax}}},$ ${{H}_{{ay}}},$ ${{H}_{{az}}}$ – проекции вектора поля анизотропии ${{\vec {H}}_{a}}$ на оси координат:

(9)

$\begin{gathered} {{H}_{{ax}}} = - \frac{1}{{{{M}_{s}}}}\frac{{\partial {{U}_{a}}}}{{\partial {{m}_{x}}}} = - \frac{1}{{{{M}_{s}}}}\left[ {2{{m}_{x}}\left( {{{K}_{1}}\left( {m_{y}^{2} + m_{z}^{2}} \right) + {{K}_{2}}m_{y}^{2}m_{z}^{2}} \right)} \right]~, \\ {{H}_{{ay}}} = - \frac{1}{{{{M}_{s}}}}\frac{{\partial {{U}_{a}}}}{{\partial {{m}_{y}}}} = - \frac{1}{{{{M}_{s}}}}\left[ {2{{m}_{y}}\left( {{{K}_{1}}\left( {m_{z}^{2} + m_{x}^{2}} \right) + {{K}_{2}}m_{z}^{2}m_{x}^{2}} \right)} \right]~, \\ {{H}_{{az}}} = - \frac{1}{{{{M}_{s}}}}\frac{{\partial {{U}_{a}}}}{{\partial {{m}_{z}}}} = - \frac{1}{{{{M}_{s}}}}\left[ {2{{m}_{z}}\left( {{{K}_{1}}\left( {m_{x}^{2} + m_{y}^{2}} \right) + {{K}_{2}}m_{x}^{2}m_{y}^{2}} \right)} \right]~. \\ \end{gathered} $

Векторное уравнение (1) в координатном выражении может быть приведено к виду:

(10)

$\begin{gathered} \frac{{\partial {{m}_{x}}}}{{\partial t}} = - \frac{{{\gamma }}}{{1 + {{{{\alpha }}}^{2}}}}\left[ {\left( {{{m}_{y}} + {{\alpha }}{{m}_{x}}{{m}_{z}}} \right){{H}_{{ez}}} - \left( {{{m}_{z}} - {{\alpha }}{{m}_{y}}{{m}_{x}}} \right){{H}_{{ey}}} - } \right.\left. {\,\,{{\alpha }}\left( {m_{y}^{2} + m_{z}^{2}} \right){{H}_{{ex}}}} \right],\,\,\,\, \\ \frac{{\partial {{m}_{y}}}}{{\partial t}} = - \frac{{{\gamma }}}{{1 + {{{{\alpha }}}^{2}}}} \times \,\,\left[ {\left( {{{m}_{z}} + {{\alpha }}{{m}_{y}}{{m}_{x}}} \right){{H}_{{ex}}} - \left( {{{m}_{x}} - {{\alpha }}{{m}_{z}}{{m}_{y}}} \right){{H}_{{ez}}} - {{\alpha }}\left( {m_{z}^{2} + m_{x}^{2}} \right){{H}_{{ey}}}} \right], \\ \frac{{\partial {{m}_{z}}}}{{\partial t}} = - \frac{{{\gamma }}}{{1 + {{{{\alpha }}}^{2}}}}\left[ {\left( {{{m}_{x}} + {{\alpha }}{{m}_{z}}{{m}_{y}}} \right){{H}_{{ey}}} - \left( {{{m}_{y}} - {{\alpha }}{{m}_{x}}{{m}_{z}}} \right){{H}_{{ex}}} - } \right.\left. {\,{{\alpha }}\left( {m_{x}^{2} + m_{y}^{2}} \right){{H}_{{ez}}}} \right]. \\ \end{gathered} $

Система уравнений (10) решалась относительно компонент вектора намагниченности m_x, m_y, m_z c использованием метода Дормана–Принса 8-го порядка с контролем погрешности интегрирования. Энергия магнитной кристаллической анизотропии была учтена в виде выражения (6), а эффективное магнитное поле рассчитано из выражений (8) и (9). Расчеты компонент вектора намагниченности проводились для частот внешнего поля от 0.1 до 4 ГГц. Постоянное магнитное поле варьировалось от 0 до 3000 Э.

РЕЗУЛЬТАТЫ РАСЧЕТОВ И ИХ АНАЛИЗ

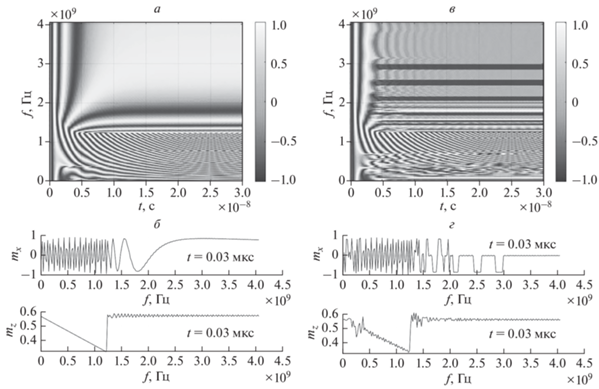
В результате численных решений системы уравнений (10) были получены временные зависимости компоненты ${{m}_{x}}$ в диапазоне частот от 0.1 до 4 ГГц, рассчитанные с учетом полей анизотропии ${{H}_{a}},$ и при их отсутствии (рис. 2). При отсутствии поля анизотропии ${{H}_{a}},$ внешнее постоянное магнитное поле компенсируется размагничивающим полем пленки вплоть до поля насыщения. В этом случае, до частоты ориентационного перехода ($\sim 1.2\,\,{\text{ГГц}}$ при $H = 1000\,\,{\text{Э}}$) вектор намагниченности вращается в плоскости пленки с частотой переменного поля. На данной частоте из-за наличия нелинейности системы происходит ориентационный переход, при этом вектор намагниченности замедляет вращение и, с ростом частоты, переориентируется в некоторое равновесное положение, совпадающее с осью легкого намагничивания. Конечное значение компонент ${{m}_{x}},$ ${{m}_{y}}$ меняется плавно с ростом частоты, поскольку в этом случае, в плоскости пленки энергия не зависит от направления (рис. 2а и 2б). В случае, когда ${{U}_{a}} \ne 0,$ минимум полной энергии имеет место при нескольких пространственно разнесенных устойчивых положениях, в которых может останавливаться вектор намагниченности. Выше частоты ориентационного перехода, при значениях внешнего поля $0 < H < 4{{\pi }}{{M}_{s}},$ которое компенсируется полем диполь-дипольного взаимодействия пленки, проекции вектора намагниченности на плоскость пленки ориентируются вдоль направлений осей легкого намагничивания [100] и [010], а образовавшаяся дискретность пространственных минимумов энергии приводит к образованию частотных щелей с резкими границами (рис. 2в и 2г). Расчеты положения вектора намагниченности в конечный момент времени, соответствующим ее установившимся колебаниям, без действия полей анизотропии, показывают, что при постоянном поле, не превышающем поле насыщения ($\sim 1750\,\,{\text{Э}}$ для железо-иттриевого граната), наблюдается обычный ферромагнитный резонанс. Ниже поля насыщения, но выше некоторой критической частоты, соответствующей ориентационному переходу [5], вектор намагниченности колеблется вокруг некоторого положения, которое плавно изменяется с ростом постоянного магнитного поля. При учете поля анизотропии вектор намагниченности принимает только четыре равновесных положения, в которые он переходит скачками, фиксируясь в одном из возможных минимумов энергии, создаваемых магнитной анизотропией кубической решетки кристалла.

Рис. 2.

Временные зависимости компоненты ${{m}_{x}}$ в диапазоне частот $0.01{\text{--}}4\,\,{\text{ГГц}}$ и частотные зависимости ${{m}_{x}},$ ${{m}_{z}}$ в момент времени $t = 0.03\,\,{\text{мкс}}$ без учета (a, б) и с учетом (в, г) магнитной анизотропии $H = 1000\,\,{\text{Э,}}$ $h = 10\,\,{\text{Э,}}$ ${{\alpha }} = 0.01.$ Слева от рисунков по вертикальной оси приведены значения ${{m}_{x}}$ в градациях цвета.

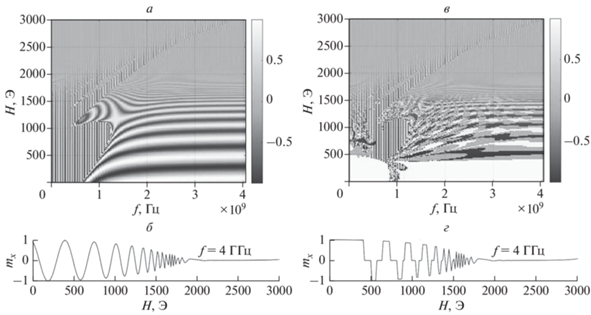
На рис. 3 показаны результаты расчета компоненты ${{m}_{x}}\left( {f,H} \right),$ как функции частоты переменного поля $~f$ и величины внешнего постоянного магнитного поля $H.$ Монотонные зависимости компонент вектора намагниченности (рис. 3а) при изменении констант анизотропии, принимают бифуркационный характер, где каждому скачку соответствует быстрый переход вектора намагниченности из одного устойчивого пространственного положения в другое. На графике это проявляется возникновением участков необычной конфигурации с большими производными (рис. 3в). На рис. 3б и 3г показаны зависимости ${{m}_{x}}\left( H \right)$ на частоте переменного поля $f = 4\,\,{\text{ГГц}}$ с учетом и без учета магнитной кристаллической анизотропии, соответственно. Подобные сложные режимы прецессии намагниченности ранее наблюдались в работах [6–9].

Рис. 3.

Частотные и полевые зависимости компоненты ${{m}_{x}}$ в моменты времени $t = 0.03\,\,{\text{мкс}},$ и зависимости компоненты ${{m}_{x}}$ от поля $H$ при $t = 0.03\,\,{\text{мкс}}$ на частоте $f = 4\,\,{\text{ГГц}}$ без учета (a, б) и с учетом (в, г) магнитной анизотропии. $h = 10\,\,{\text{Э}},$ ${{\alpha }} = 0.01.$ Слева от рисунков по вертикальной оси приведены значения ${{m}_{x}}$ в градациях цвета.

ЗАКЛЮЧЕНИЕ

Выполнено моделирование динамики колебаний вектора намагниченности магнитной пленки с параметрами железоиттриевого граната при возбуждении пленки переменным магнитным полем с амплитудой $10\,\,{\text{Э}}$ и частотой $0.1{\text{--}}4\,\,{\text{ГГц}}.$ Переменное магнитное поле включается в начальный момент времени и действует на пленку до окончания численного эксперимента. При решениях уравнений предполагалось, что постоянное магнитное поле направлено перпендикулярно плоскости пленки и варьировалось от 0 до 3 кЭ. В начальный момент времени вектор намагниченности был направлен перпендикулярно плоскости пленки. При расчетах компонент вектора намагниченности предполагалось, что плоскость вращения вектора переменного магнитного поля совпадает с плоскостью пленки. В результате анализа полученных результатов, было обнаружено, что при некоторых значениях констант магнитной анизотропии, и при условии, что постоянное магнитное поле, меньше поля насыщения пленки, возникает бифуркационный характер поведения вектора намагниченности. Резкие скачки на графиках движения вектора намагниченности объясняются быстрыми переходами между энергетическими минимумами пленки, создаваемыми благодаря наличию магнитной кристаллической анизотропии. Особенно хорошо, наблюдаются, такие резкие скачки на частотах, превышающих частоты ориентационного перехода.

Исследование выполнено при финансовой поддержке Российского научного фонда (проект № 21-72-20048).

Список литературы

Балбашов А.М., Червоненкис А.Я. Магнитные материалы для микроэлектроники. М.: Энергия, 1979. 217 с.
Гуревич А.Г. Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука, 1973. 592 с.
Власов В.С., Котов Л.Н., Шавров В.Г. и др. // Радиотехн. и электрон. 2009. Т. 54. № 7. С. 874; Vlasov V.S., Kotov L.N., Shavrov V.G. et al. // J. Commun. Technol. Electron. 2009. V. 54. No. 7. P. 832.
Besse V., Golov A.V., Vlasov V.S. et al. // JMMM. 2020. V. 502. Art. No. 166320.
Шавров В.Г., Щеглов В.И. Ферромагнитный резонанс в условиях ориентационного перехода. М.: Физматлит, 2018. 560 с.
Шутый А.М., Семенцов Д.И. // ФТТ. 2007. Т. 49. № 9. С. 1636; Shutyi A.M., Sementsov D.I. // Phys. Solid State. 2007. V. 49. No. 9. P. 1715.
Ferona A.M., Camley R.E. // Phys. Rev. B. 2017. V. 95. Art. No. 104421.
Власов В.С., Котов Л.Н., Липина Е.С. и др. // Изв. РАН. Сер. физ. 2013. Т. 77. № 10. С. 1459; Vlasov V.S., Kotov L.N., Lipina E.S. et al. // Bull. Russ. Acad. Sci. Phys. 2013. V. 77. No. 10. P. 1255.
Плешев Д.А., Асадуллин Ф.Ф., Оганезова Н.А. и др. // Изв. РАН. Сер. физ. 2019. Т. 83. № 7. С. 987; Pleshev D.A., Asadullin F.F., Oganezova N.A. et al. // Bull. Russ. Acad. Sci. Phys. 2019. V. 83. No. 7. P. 901.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал