1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 6, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 6, стр. 792-796

Световые пули в графеновых системах: от идеальных систем к реальным

М. Б. Белоненко 1, *, Н. Н. Конобеева 1

1 Федеральное государственное автономное образовательное учреждение высшего образования “Волгоградский государственный университет”
Волгоград, Россия

* E-mail: belonenko@volsu.ru

Поступила в редакцию 24.12.2021
После доработки 17.01.2022
Принята к публикации 21.02.2022

Полный текст (PDF)

Аннотация

Исследовано распространение световой пули в графеновых системах, как в идеальных, так и реальных (например, содержащих примеси, испытывающих деформации). Построены модели взаимодействия световых пуль с такими средами. Изучены особенности динамики локализованного оптического импульса от различных параметров задачи. Выявлены контролирующие параметры, позволяющие управлять интенсивностью, а также формой световой пули.

ВВЕДЕНИЕ

В последние два десятилетия возрос интерес исследователей к так называемым световым пулям, под которыми понимаются импульсы высокой энергии, сохраняющие свою пространственную и временную локализацию, и распространяющиеся в среде без изменения их формы [1]. Возникновение световых пуль обязано балансу между процессами дифракции, нелинейности и аномальной дисперсии. Также стоит отметить, что их существование получило и экспериментальное подтверждение [2–5].

В этой связи нужно сказать, что особенно привлекательными с точки зрения стабильного распространения световых пуль являются среды, содержащие графеновые системы (углеродные нанотрубки (УНТ), графен) [6, 7]. Стоит отметить, что данные среды могут быть как идеальными в отсутствии примесей, дефектов и деформаций, так и реальными. С одной стороны, задачей экспериментаторов является получение “чистого” материала [8], причем этап избавления от примеси независимо от способа синтезирования является самым трудоемким и ресурсозатратным. Существует множество методов очистки. Упомянем лишь некоторые из них. Первый сочетает в себе кипячение УНТ в кислоте и окисление в газовой фазе [9, 10]. Отметим также метод ECR-CVD [11, 12] для получения вертикально ориентированных (что важно в контексте нашей модели) аморфных УНТ, который защищает от ионного повреждения и присутствия примесей в материале.

С другой стороны, химическая, топологическая или механическая модификация графеноподобных материалов расширяет диапазон использования последних за счет того, что существенно изменяются электронные свойства углеродных систем [13–15].

С этой точки зрения, важно изучать распространение световых пуль в средах, содержащих, как “чистые”, так и измененные за счет введения примесей, дефектов или деформаций, углеродные материалы. Поскольку это поможет пролить свет на особенности взаимодействия электромагнитного излучения с такими материалами, и, следовательно, будет способствовать разработке новых устройств современной нелинейной оптики, а также верифицировать их работу под нагрузкой.

МОДЕЛЬ И ОСНОВНЫЕ УРАВНЕНИЯ

Опишем геометрию задачи. В случае графена волновой вектор направлен перпендикулярно его монослоям, а вектор напряженности электрического поля – вдоль графеновой плоскости. В задачах с углеродными нанотрубками импульс бежит под углом в 90° к массиву УНТ, а поле направлено вдоль их осей и сонаправлено с электрическим током.

Отметим, что математическая модель, описывающая взаимодействие электромагнитного излучения с системой, как идеальной, так и реальной имеет следующий вид:

(1)
$\Delta \vec {A} - \frac{\varepsilon }{{{{с}^{2}}}}\frac{{\partial{ \vec {A}}}}{{\partial t}} + \frac{{4\pi }}{c}\vec {j}\left( {\vec {A}} \right) = 0,$
где $\vec {A}$ – векторный потенциал электрического поля, ε – диэлектрическая проницаемость среды, которая содержит графеновый материал, c – скорость света, $\vec {j}$ – плотность тока проводимости. Далее в зависимости от размерности задачи необходимо учесть соответствующее количество ненулевых компонент векторного потенциала и определить величину плотности тока вдоль оси УНТ:

(2)
$j = 2e\sum\limits_{s = 1}^m {\int\limits_{1st\;BZ} {\upsilon \cdot f\left( {p,s} \right)dp} } ,$

здесь e – заряд электрона, $\upsilon = {{\partial \Delta } \mathord{\left/ {\vphantom {{\partial \Delta } {\partial p}}} \right. \kern-0em} {\partial p}}$ – скорость электрона, $\Delta $ задает электронный энергетический спектр УНТ (идеальной [6] или примесной [16]) или графена, $f\left( {p,s} \right)$ – функция распределения электронов по квазиимпульсу p и числам s, характеризующим квантование импульса электрона по периметру нанотрубки (графена в случае больших m), интегрирование по квазиимпульсу ведется по первой зоне Бриллюэна.

Поскольку вектор напряженности параллелен оси УНТ или плоскости листа графена, то требуется записать только уравнение на одну компоненту векторного потенциала электрического поля, которая в зависимости от размерности задачи может зависеть от одной, двух или трех пространственных координат, не считая одной временной.

В силу вычислительных ограничений в случае трехмерной задачи нами используется подход, связанный с переходом в цилиндрическую систему координат, когда уравнение (1) приобретает вид:

(3)
$\begin{gathered} \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial{ \vec {A}}}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{z}^{2}}}} + \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{\varphi }^{2}}}} - \\ - \,\,\frac{\varepsilon }{{{{с}^{2}}}}\frac{{\partial{ \vec {A}}}}{{\partial t}} + \frac{{4\pi }}{c}\vec {j}\left( {\vec {A}} \right) = 0. \\ \end{gathered} $

Причем в дальнейшем производную по φ можно не рассматривать согласно результатам работы [17].

Отметим также, что довольно просто учесть воздействие механической нагрузки на рассматриваемую систему, которое приводит к появлению дополнительного поля напряжений. Его легко учесть в рамках калибровочной теории [18]. В результате чего получаем сумму соответствующих векторных потенциалов (электромагнитного поля импульса $\vec {A}$ и калибровочного $\vec {B}$):

(4)
$\Delta \vec {A} - \frac{\varepsilon }{{{{с}^{2}}}}\frac{{\partial{ \vec {A}}}}{{\partial t}} + \frac{{4\pi }}{c}\vec {j}\left( {\vec {A} + \vec {B}} \right) = 0.$

Далее, учитывая конкретный вид закона дисперсии электронов и раскладывая скорость носителей заряда в ряд Фурье, получим следующее типичное выражение для плотности тока:

(5)
$\begin{gathered} {{j}_{0}} = - e{{n}_{0}}\sum\limits_k {{{D}_{k}}\sin \left( {\frac{{ke}}{c}A\left( t \right)} \right)} , \\ {{D}_{k}} = \sum\limits_{s = 1}^m {\int\limits_{ - {\pi \mathord{\left/ {\vphantom {\pi a}} \right. \kern-0em} a}}^{{\pi \mathord{\left/ {\vphantom {\pi a}} \right. \kern-0em} a}} {dp{\kern 1pt} '{{A}_{{ks}}}} } \cos \left( {kp{\kern 1pt} '} \right) \times \\ \times \,\,\frac{{\exp \left( { - {{\Delta \left( {p{\kern 1pt} ',s} \right)} \mathord{\left/ {\vphantom {{\Delta \left( {p{\kern 1pt} ',s} \right)} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right)}}{{1 + \exp \left( { - {{\Delta \left( {p{\kern 1pt} ',s} \right)} \mathord{\left/ {\vphantom {{\Delta \left( {p{\kern 1pt} ',s} \right)} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right)}}, \\ \end{gathered} $
где ${{n}_{0}}$ – концентрация электронов, kB = 1.38 · · 10–23 Дж/К, Т – температура, ${{A}_{{ks}}}$– коэффициенты разложения в ряд Фурье.

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Исследуемое уравнение (1) с учетом формулы (5) решалось численно [19]. Начальное условие выбиралось в гауссовом виде, граничные условия – типа Неймана. Эволюция интенсивности электромагнитного поля $I\left( {r,z,t} \right)$ = ${{E}^{2}}\left( {r,z,t} \right)$ в трехмерном случае показана на рис. 1.

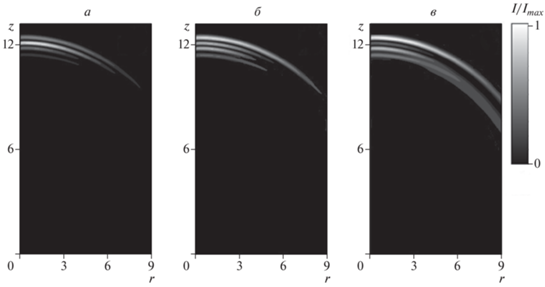
Рис. 1.

Интенсивность трехмерного электромагнитного импульса в различные моменты времени для массива “идеальных” УНТ (а–в) и для среды без УНТ (г–е): t = 0.8 ⋅ 10–13 (а, г); 1.6 ⋅ 10–13 (б, д); 2.6 ⋅ 10–13 c (в, е). I0 – максимальное значение интенсивности.

Рисунок 1 демонстрирует стабильное распространение импульса в среде с “идеальными” УНТ. Причем, как видно, введение в среду нанотрубок способствует локализации энергии импульса и уменьшению его дисперсии по сравнению со случаем распространения импульса в среде, не содержащей нанотрубок. Отметим, что скорость импульса при этом уменьшается.

Влияние примеси, содержащейся в УНТ, показано на рис. 2. Здесь мы рассматриваем многоуровневую модель [16], в которой учтены переходы между подрешетками УНТ и уровнями примеси (параметр ρ описывает энергию этих переходов в единицах интеграла перескока γ = 2.7 эВ). Видно, что введение примеси с одной стороны приводит к уменьшению амплитуды импульса, а с другой – к увеличению его скорости. При этом наблюдается уменьшение продольной дисперсии импульса. Стоит отметить, нетривиальный характер зависимости от параметра ρ, поскольку при его увеличении изменение амплитуды и скорости импульса немонотонно.

Рис. 2.

Зависимость интенсивности трехмерного электромагнитного импульса от параметров примеси (t = 2.6 ⋅ 10–13 c). Построены срезы при r = 0: ρ = 0 (а); 0.1γ (б); 0.5γ (в); γ (г). Imax – максимальное значение интенсивности.

Зависимость формы импульса от величины механической нагрузки, приложенной к углеродным нанотрубкам показана на рис. 3.

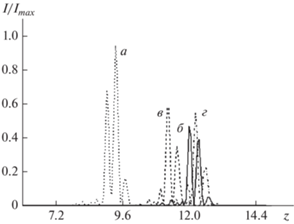
Рис. 3.

Интенсивность электрического поля трехмерного электромагнитного импульса при распространении в механически напряженной среде с УНТ (при t = 2.6 ⋅ 10–13 c): Для кривой (в) нагрузка в 5 раз больше, чем для (а), для кривой (б) нагрузка в 3 раза больше, чем для (а). Imax – максимальное значение интенсивности.

Из приведенных графиков можно сделать вывод, что увеличение величины тензора деформации приводит к увеличению как продольной, так и поперечной дисперсии импульса. Также отметим, что импульс распадается на несколько разных по амплитуде, причем количество этих дополнительных пиков увеличивается с ростом механической нагрузки.

ЗАКЛЮЧЕНИЕ

Разработана модель для описания взаимодействия световых пуль со средой, содержащей графеновые материалы (идеальные и реальные) в одно, двух и трехмерном случае. Показано, что легирование углеродных нанотрубок примесью позволяет управлять динамикой предельно короткого оптического импульса, за счет модификации нелинейных свойств массива нанотрубок, а, следовательно, изменения баланс между дифракционным расплыванием импульса и нелинейностью среды, в которой происходит распространение. Обнаружено, что при уменьшении величины деформации импульс становится более локализованным. Таким образом, механическое напряжение является контролирующим параметром для электромагнитного поля.

Численное моделирование выполнено в рамках работ по теме государственного задания Министерства науки и высшего образования РФ (проект № 0633-2020-0003).

Список литературы

  1. Silberberg Y. // Opt. Lett. 1990. V. 15. P. 1282.

  2. Renninger W.H., Wise F.W. // Nature Commun. 2013. V. 4. No. 1. P. 1719.

  3. Panagiotopoulos P., Whalen P., Kolesik M. et al. // Nature Photon. 2015. V. 9. No. 8. P. 543.

  4. Li Z., Kawanaka J. // Commun. Phys. 2020. V. 3. Art. No. 211.

  5. Залозная Е.Д., Дормидонов А.Е., Компанец В.О. и др. // Письма в ЖЭТФ. 2021. Т. 113. № 12. С. 817; Zaloznaya E.D., Dormidonov A.E., Kompanets V.O. et al. // JETP Lett. 2021. V. 113. No. 12. P. 787.

  6. Харрис П. Углеродные нанотрубы и родственные структуры. Новые материалы XXI века. М.: Техносфера, 2003. 336 с.

  7. Novoselov K.S., Geim A.K., Morozov S.V. et al. // Science. 2004. V. 306. P. 666.

  8. Yang S., Brüller S., Wu Z.-S. et al. // J. Amer. Chem. Soc. 2015. V. 137. No. 43. Art. No. 13927.

  9. Park Y.S., Bae D.J. // J. Phys. Chem. 2001. V. 105. P. 5677.

  10. Zimmerman J.L., Bradley R.K., Huffman C.B. et al. // Chem. Mater. 2000. V. 12. P. 1361.

  11. Lassig S.E., Tucker J.D. // Microelectron. J. 1995. V. 26. No. 8. Art. No. XI.

  12. Wang Z., Ba D., Caoc P. et al. // Mater. Sci. Engin. B. 2007. V. 140. P. 44.

  13. Araujo P.T., Terrones M., Dresselhaus M.S. // Mater Today. 2012. V. 15. No. 3. P. 98.

  14. Ha B., Lee C.J. // Appl. Phys. Lett. 2007. V. 90. Art. No. 023108.

  15. Konobeeva N.N. // J. Nano-Electr. Phys. 2017. V. 9. No. 5. Art. No. 05049.

  16. Zhukov A.V., Bouffanais R., Konobeeva N.N. et al. // EPL. 2014. V. 106. Art. No. 37005.

  17. Zhukov A.V., Bouffanais R., Fedorov E.G. et al. // J. Appl. Phys. 2013. V. 114. Art. No. 143106.

  18. Vozmediano M.A.H., Katsnelson M.I., Guinea F. // Phys. Rep. 2010. V. 496. P. 109.

  19. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука, 1987. 601 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал