1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 7, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 7, стр. 985-988

Дальние корреляции в граничных слоях жидкостей

Ю. В. Аграфонов 1, *, И. С. Петрушин 1, Д. В. Халаимов 1

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Иркутский государственный университет”
Иркутск, Россия

* E-mail: agrafonov@physdep.isu.ru

Поступила в редакцию 14.02.2022
После доработки 28.02.2022
Принята к публикации 23.03.2022

Полный текст (PDF)

Аннотация

Рассмотрено решение линейного интегрального уравнения Фредгольма второго рода для одночастичной функции распределения молекулярной системы твердых сфер в контакте с твердой поверхностью. Граничным условием служит двухчастичная функция распределения макроскопической жидкости. Решение для одночастичной функции асимптотически показывает возникновение медленно затухающих осцилляций при высоких плотностях.

ВВЕДЕНИЕ

Данная работа посвящена разработке методов решения линейного интегрального уравнения для одночастичной функции распределения с целью выявления дальнодействующих (асимптотических) корреляций локальной плотности в граничных слоях жидкостей.

Одной из принципиальных задач теории жидкостей является исследование особенностей ближнего порядка и формулировка уравнений для частичных функций распределения, наиболее точно описывающих эти особенности. Тем не менее, существуют явления в жидких системах, свойства которых определяются именно асимптотическими свойствами корреляционных функций. К ним относятся свойства систем на границе раздела фаз, изменение локальной структуры жидкостей в ограниченных объемах, явления смачивания и многие другие.

Аналогичные проблемы возникают при рассмотрении структуры поверхностных слоев аморфных (диэлектрических) пленок, получаемых быстрым охлаждением расплава. В работах [1–5] разработана программа исследования структурных характеристик поверхностных аморфных пленок на границе с твердой поверхностью. Отметим также, что при медленном охлаждении расплава структурные характеристики кристалла в некоторых случаях, также определяются дальними корреляциями. Например, первые координационные числа для гранецентрированной и гексагональной структуры полностью совпадают. Тонкие различия проявляются в дальних координационных сферах.

Таким образом, исследование асимптотического поведения корреляционных функций выявляет общие закономерности в структурах различных конденсированных сред.

ПОСТАНОВКА ЗАДАЧИ

Современная статистическая физика жидкостей базируется на уравнениях Орнштейна–Цернике [6, 7] для одно- и двух- частичных функций распределения

(1)
$\begin{gathered} {{{{\omega }}}_{1}} = n\int {{{G}_{2}}С_{{12}}^{{\left( 1 \right)}}d\left( 2 \right)} + {{\mu }}, \\ {{h}_{{12}}} = C_{{12}}^{{\left( 2 \right)}} + n\int {{{G}_{3}}C_{{13}}^{{\left( 2 \right)}}{{h}_{{23}}}d\left( 3 \right)} . \\ \end{gathered} $
Здесь d(i) ≡ dri означает интегрирование по координатам i-й частицы; n – плотность жидкости; Gi = exp(–Φi/kT + ωi) – однoчастичная функция распределения, описывающая положение частицы в лабораторной системе координат; Φi – потенциальная энергия частицы во внешнем поле; ωi – одночастичный термический потенциал, учитывающий взаимодействие частицы с окружающей средой; химический потенциал µ находится из условия перехода к пространственно-однородной системе; парная корреляционная функция hij = [exp(–Φij/kT + ωij) – 1] связана с двухчастичной функцией распределения соотношением Gij = GiGj(1 + hij); ωij – двухчастичный термический потенциал учитывает коллективное взаимодействие двух частиц через их окружение; $C_{{ij}}^{{(k)}}$ – прямые корреляционные функции:
(2)
$\begin{gathered} С_{{ij}}^{{\left( 1 \right)}} = {{h}_{{ij}}} - {{{{\omega }}}_{{ij}}} - \frac{1}{2}{{h}_{{ij}}}\left( {{{{{\omega }}}_{{ij}}} + M_{{ij}}^{{\left( 1 \right)}}} \right), \\ C_{{ij}}^{{\left( 2 \right)}} = {{h}_{{ij}}} - {{{{\omega }}}_{{ij}}} + M_{{ij}}^{{\left( 2 \right)}}, \\ \end{gathered} $
Здесь $M_{{ij}}^{{\left( 1 \right)}},$ $M_{{ij}}^{{\left( 2 \right)}}$ – бесконечные функциональные ряды от искомых функций распределения. При решении конкретных задач $M_{{ij}}^{{\left( 1 \right)}},$ $M_{{ij}}^{{\left( 2 \right)}}$ аппроксимируют простыми аналитическими выражениями, что приводит к нелинейным интегральным уравнениям. Наиболее известными из них являются гиперцепное, Перкуса–Йевика, Мартынова–Саркисова. Подчеркнем, что приближение Перкуса–Йевика является единственным, которое допускает аналитическое решение для пространственно-однородных трехмерных молекулярных систем [8]. В последние годы разрабатываются аналитические методы решения для одномерных и двумерных молекулярных систем [9]. Отметим также интенсивно развивающееся направление по аморфизации макроскопических растворов [11–17], за которое была присуждена Нобелевская премия по физике 2021 г.

Для пространственно-неоднородных систем функции ${{G}_{1}} = {{G}_{1}}\left( {{{{\vec {r}}}_{1}}} \right),$ ${{G}_{{12}}} = {{G}_{{12}}}\left( {{{{\vec {r}}}_{1}},{{{\vec {r}}}_{2}}} \right)$ позволяют описать микроструктуру вещества вблизи твердой ограничивающей поверхности и рассчитать термодинамические параметры. Заметим, что решение уравнений (1) и (2) для этих функций многих переменных является сложной вычислительной задачей. Эту проблему обходят заменой прямой корреляционной функции $C_{{12}}^{{\left( 1 \right)}}\left( {{{{\vec {r}}}_{1}},{{{\vec {r}}}_{2}}} \right)$ ее граничным значением $C_{{12}}^{{\left( 1 \right)}}\left( {{{r}_{{12}}}} \right).$ В зависимости от применяемой аппроксимации получают то или иное уравнение на одночастичную функцию распределения (синглетное приближение), описывающую профиль локальной плотности n(z1) = = nG1(z1) = nexp(ω1(z1)) вблизи твердой поверхности. Все они являются нелинейными интегральными уравнениями и решаются численно. Анализ численных решений приведен в работе [10].

ЛИНЕЙНОЕ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ

В наших работах [3–5] предложена модификация синглетного приближения в форме линейного интегрального уравнения Фредгольма второго рода

(3)
$\begin{gathered} \left( {{{e}^{{{{{{\omega }}}_{1}}\left( {{{z}_{1}}} \right)}}} - 1} \right) - 2{{\pi }}n\int\limits_0^\infty {d{{z}_{2}}\left( {{{e}^{{{{{{\omega }}}_{1}}\left( {{{z}_{2}}} \right)}}} - 1} \right)} \int\limits_{\left| {{{z}_{{12}}}} \right|}^\infty {{{r}_{{12}}}d{{r}_{{12}}}C_{{12}}^{{\left( {1,0} \right)}}\left( {{{r}_{{12}}}} \right)} = \\ = - 2{{\pi }}n\int\limits_{{{z}_{1}}}^\infty {d{{z}_{{12}}}} \int\limits_{{{z}_{{12}}}}^\infty {{{r}_{{12}}}d{{r}_{{12}}}C_{{12}}^{{\left( {1,0} \right)}}\left( {{{r}_{{12}}}} \right)} . \\ \end{gathered} $
Здесь учтено, что взаимодействие частиц жидкости с поверхностью осуществляется как взаимодействие твердых сфер. Ядро уравнения и правая часть предварительно вычисляются из соответствующего интегрального уравнения для двухчастичной функции распределения макроскопической жидкости [6, 7]. В том случае, когда двухчастичная функция распределения вычисляется аналитически, данное уравнение также может быть решено аналитически. В частности, для замыкания Перкуса–Йевика [6, 7] внутренние интегралы уравнения (1) можно представить в виде
(4)
$\begin{gathered} K\left( {\left| z \right|} \right) = - {{\theta }}\left( {1 - \left| z \right|} \right){{\Psi }}\left( {\left| z \right|} \right), \\ {{\Psi }}\left( {\left| z \right|} \right) = \int\limits_{\left| z \right|}^1 {{{r}_{{12}}}d{{r}_{{12}}}\left( {{{\alpha }} + {{\beta }}{{r}_{{12}}} + {{\gamma }}r_{{12}}^{3}} \right)} , \\ \end{gathered} $
где

(5)
$\begin{gathered} {{\alpha }} = {{{{{(2{{\eta }} + 1)}}^{2}}} \mathord{\left/ {\vphantom {{{{{(2{{\eta }} + 1)}}^{2}}} {{{{({{\eta }} - 1)}}^{4}}}}} \right. \kern-0em} {{{{({{\eta }} - 1)}}^{4}}}},\,\,\,\,{{\beta }} = {{ - 3{{\eta }}{{{(2 + {{\eta }})}}^{2}}} \mathord{\left/ {\vphantom {{ - 3{{\eta }}{{{(2 + {{\eta }})}}^{2}}} {2{{{({{\eta }} - 1)}}^{4}}}}} \right. \kern-0em} {2{{{({{\eta }} - 1)}}^{4}}}}, \\ {{\gamma }} = {{{{\eta }}{{{(2{{\eta }} + 1)}}^{2}}} \mathord{\left/ {\vphantom {{{{\eta }}{{{(2{{\eta }} + 1)}}^{2}}} {2{{{({{\eta }} - 1)}}^{4}}}}} \right. \kern-0em} {2{{{({{\eta }} - 1)}}^{4}}}}. \\ \end{gathered} $

В результате уравнение принимает вид

(6)
$\begin{gathered} f\left( {{{z}_{1}}} \right) = - 12{{\eta }}\int\limits_0^{1 + {{z}_{1}}} {d{{z}_{2}}f\left( {{{z}_{2}}} \right){{\Psi }}\left( {\left| {{{z}_{1}} - {{z}_{2}}} \right|} \right)} + \\ + \,\,12{{\eta }}\int\limits_{{{z}_{1}}}^1 {d{{z}_{2}}{{\Psi }}\left( {{{z}_{2}}} \right)} ,\,\,\,\,~{{z}_{1}} \leqslant 1, \\ \end{gathered} $
(7)
$f\left( {{{z}_{1}}} \right) = - 12{{\eta }}\int\limits_{{{z}_{1}} - 1}^{{{z}_{1}} + 1} {d{{z}_{2}}f\left( {{{z}_{2}}} \right){{\Psi }}\left( {\left| {{{z}_{1}} - {{z}_{2}}} \right|} \right)} ,\,\,\,\,{{z}_{1}} \geqslant 1,$
где мы обозначили: η = πn/6, f(z1) = exp(ω1(z1)) – 1. Из (3) вытекает, что для вычисления функции на интервале 0 ≤ z1 ≤ 1 необходимо знать, ее поведение на интервале 1 ≤ z1 ≤ 2 и т.д. В результате имеем бесконечную цепочку “зацепляющихся” функций fn(z1), n ≤ z1 ≤ n + 1, (n = 0, 1, 2, 3, …). Тем не менее, асимптотическое решение уравнения (7) можно легко найти. Удобно предварительно продифференцировать (7) по параметру z1. Учитывая, что Ψ(1) = 0, получим

(8)
$\begin{gathered} \frac{d}{{d{{z}_{1}}}}f\left( {{{z}_{1}}} \right) = - 12{{\eta }}\left( {\int\limits_{{{z}_{1}} - 1}^{{{z}_{1}}} {d{{z}_{2}}f\left( {{{z}_{2}}} \right)} {{{{\Psi }}}^{{\left( 1 \right)}}}\left( {{{z}_{1}} - {{z}_{2}}} \right) - } \right. \\ - \,\,\int\limits_{{{z}_{1}}}^{{{z}_{1}} + 1} {f\left( {{{z}_{2}}} \right){{{{\Psi }}}^{{\left( 1 \right)}}}\left( {{{z}_{2}} - {{z}_{1}}} \right)} . \\ \end{gathered} $

Решение данного уравнения представляем в виде

(9)
$f\left( {{{z}_{1}}} \right) = {{e}^{{ - {{k}_{1}}{{z}_{1}}}}}\left( {A\sin {{k}_{2}}{{z}_{1}} + B\cos {{k}_{2}}{{z}_{1}}} \right).$

Подставляя искомое решение в (8), получим систему трансцендентных уравнений для определения волновых чисел

(10)
$\begin{gathered} {{k}_{1}} = 12{{\eta }}\int\limits_0^1 {dt{{{{\Psi }}}^{{\left( 1 \right)}}}} \left( t \right)\cos {{k}_{2}}t\sinh {{k}_{1}}t, \\ {{k}_{2}} = 12{{\eta }}\int\limits_0^1 {dt{{{{\Psi }}}^{{\left( 1 \right)}}}} \left( t \right)\sin {{k}_{2}}t\cosh {{k}_{1}}t. \\ \end{gathered} $

Амплитуды A, B остаются произвольными. Таким образом асимптотика носит осциллирующий, затухающий характер. Численное решение системы трансцендентных уравнений (10) проводится методом последовательных приближений для плотностей жидкости η в диапазоне от 0.26 до 0.785. В таблице приведены значения волновых векторов k1 и k2.

Таблица 1.

Значения волновых чисел в зависимости от плотности

K1 K2 n(*π/6)
4.2383 4.9055 0.5
3.7807 5.1341 0.6
3.3601 5.38906 0.7
2.97 5.6717 0.8
2.6064 5.9819 0.9
2.26497 6.31825 1.0
1.9406 6.6774 1.1
1.62667 7.0535 1.2
1.31544 7.4358 1.3
1.002 7.806 1.4
0.6922 8.1387 1.5

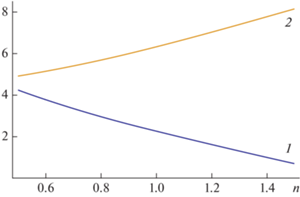
На рис. 1 показаны графики коэффициентов k1 и k2 в зависимости от плотности жидкости.

Рис. 1.

График зависимости коэффициентов k1 (1) и k2 (2) от плотности.

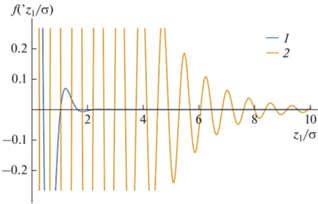
При малых и средних плотностях преобладает монотонное, короткодействующее убывание одночастичной функции распределения, обусловленное коллективными эффектами потенциала твердых сфер. С ростом плотности возникают осцилляции, вызванные эффектами плотной упаковки твердых сфер. Примерную картину поведения одночастичной функции распределения на всем интервале расстояний z ≥ 0 можно получить, подставив найденные волновые числа в функцию (6) с произвольными амплитудами A, B (рис. 2).

Рис. 2.

График одночастичной функции распределения при низких и высоких плотностях: (1) n = 0.3141, (2) n = 0.785.

ЗАКЛЮЧЕНИЕ

Рассмотрено уравнение для молекулярной системы твердых сфер вблизи твердой поверхности. Уравнение имеет вид линейного интегрального уравнения Фредгольма второго рода. Ядро и правая часть уравнения вычислены нами в приближении Перкуса–Йевика. Решение имеет осциллирующий, затухающий вид. Волновые числа, определяющие скорость затухания и период осцилляций находятся численным решением двух трансцендентных уравнений. Численное решение данных уравнений показало, что при малой плотности молекулярной системы затухание носит короткодействующий характер. Однако с ростом плотности осцилляции носят дальнодействующий характер, что обусловлено эффектами плотной упаковки твердых сфер. Полученное решение можно обобщить на молекулярные системы с реалистичными потенциалами межчастичного взаимодействия. Таким образом, исследование асимптотического поведения корреляционных функций позволит выявлять общие закономерности в структурах различных конденсированных сред.

Исследования проведены при частичной поддержке Минобрнауки РФ в рамках выполнения государственного задания РФ (проект № 3.1941.2017/ПЧ).

Список литературы

  1. Agrafonov Y., Petrushin I. // Phys. Proc. 2015. V. 71. P. 364.

  2. Agrafonov Y., Petrushin I. // J. Phys. Conf. Ser. 2016. V. 747. Art. No. 012024.

  3. Agrafonov Yu.V., Petrushin I.S. // Cond. Matter Interphases. 2020. V. 22. No. 2. P. 291.

  4. Аграфонов Ю.В., Петрушин И.С. // Изв. РАН. Сер. физ. 2020. Т. 84. № 7. С. 951; Agrafonov Y.V., Petrushin I.S. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. No. 7. P. 783.

  5. Agrafonov Yu.V., Petrushin I.S. // J. Phys. Conf. Ser. 2020. V. 1686. Art. No. 012039.

  6. Martynov G.A. Fundamental theory of liquids: method of distribution functions. Bristol, Philadelphia, N.Y.: Adam Hilger, 1992. P. 470.

  7. Саркисов Г.Н. // УФН. 2002. Т. 172. № 6. С. 647; Sarkisov G.N. // Phys. Usp. 2002. V. 45. No. 6. P. 597.

  8. Wertheim M.S. // Phys. Rev. Lett. 1963. V. 10. No. 8. P. 321.

  9. He Y., Rice S. A., Xu X. // J. Chem. Phys. 2016. V. 145. № 23. Art. No. 234508.

  10. Tikhonov D.A., Kiselyov O.E., Martynov G.A., Sarkisov G.N. // J. Mol. Liq. 1999. V. 82. No. 1–2. P. 3.

  11. Mézard M., Parisi G. // J. Phys. Cond. Matter. 1999. V. 11. No. 10A. Art. No. A157.

  12. Bomont J.-M., Hansen J.-P., Pastore G. // J. Chem. Phys. 2019. V. 150. No. 15. Art. No. 154504.

  13. Bomont J.-M., Hansen J.-P., Pastore G. // Phys. Rev. E. 2015. V. 92. № 4. Art. No. 042316.

  14. Bomont J.-M., Hansen J.-P., Pastore G. // J. Chem. Phys. 2014. V. 141. No. 17. Art. No. 174505.

  15. Bomont J.-M., Pastore G., Hansen J.-P. // J. Chem. Phys. 2017. V. 146. No. 11. Art. No. 114504.

  16. Parisi G., Seoane B. // Phys. Rev. E. 2014. V. 89. No. 2. Art. No. 022309.

  17. Rogers D.M. // arXiv: 1807.05963. 2018.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал