1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 7, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 7, стр. 1037-1041

Асимптотически точные оценки погрешности для экспоненциально сходящихся квадратур

В. С. Хохлачев 1, *, А. А. Белов 1, 2

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”, физический факультет
Москва, Россия

2 Федеральное государственное автономное образовательное учреждение высшего образования “Российский университет дружбы народов”
Москва, Россия

* E-mail: valentin.mycroft@yandex.ru

Поступила в редакцию 14.02.2022
После доработки 28.02.2022
Принята к публикации 23.03.2022

Полный текст (PDF)

Аннотация

Во многих прикладных задачах требуется экономичное вычисление квадратур с высокой точностью. Для некоторых частных, но важных для практики случаев квадратуры трапеций и средних дают не квадратичную, а экспоненциальную сходимость по величине шага сетки. В данной работе построены новые асимптотически точные оценки погрешности таких квадратур. Предложена процедура экстраполяции погрешности, которая кардинально повышает точность расчета.

ВВЕДЕНИЕ

Приведем примеры физических задач, в которых возникают экспоненциально сходящиеся квадратуры.

1. Функция Ламберта $W\left( x \right).$ Данная специальная функция является точным решением задачи об электрической цепи, содержащей постоянный источник питания, сопротивление и полупроводниковый диод. Эта функция используется для расчета цепей сложной конфигурации с полупроводниковыми диодами. В книге [1] можно найти большое количество ее приложений в физике. Представление этой функции тригонометрическим интегралом, зависящим от параметра, приведено в статье [2]. Там же представлены численные расчеты, которые показывают экспоненциальную скорость сходимости формулы трапеций для этого интеграла.

2. В задачах обработки сигналов нужно раскладывать заданную функцию в ряд либо интеграл Фурье. В первом случае нужно вычислять интеграл от периодической функции по полному периоду; во втором – интеграл по числовой прямой от функции, быстро убывающей на бесконечности. В обоих случаях формула трапеций сходится экспоненциально.

3. Решение ряда физических задач можно построить с помощью преобразования Лапласа. Примерами являются расчеты электротехнических цепей (приводящие к решению линейных ОДУ), нахождение сечения реакции по ее скорости (с помощью решения уравнения Фредгольма первого рода) и т.д. С помощью специальных замен переменных интегралы в прямом и обратном преобразованиях Лапласа могут быть вычислены экспоненциально сходящимися квадратурами [3–7].

4. Решение краевых задач для уравнений в частных производных (включая задачи на собственные значения), записанных в интегральной форме. Примерами являются задача рассеяния, приводящая к интегральному уравнению Липпмана–Швингера, квантово-механические задачи на собственные значения, описываемые интегральной формой уравнения Шрёдингера и ряд других.

Для сеточного вычисления квадратур обычно используют методы трапеций, средних и Симпсона. Обычно погрешность этих методов квадратично зависит от шага, и для получения хорошей точности требуется большое число шагов.

Однако существует ряд случаев, когда погрешность метода трапеций зависит от величины шага экспоненциально, т.е. при уменьшении шага вдвое число верных знаков примерно удваивается. Эта скорость сходимости аналогична таковой в методе Ньютона. Такими случаями являются интеграл от периодической функции по полному периоду и интеграл по всей числовой прямой от функции, достаточно быстро убывающей на бесконечности.

Если подынтегральная функция имеет полюса первого порядка в комплексной плоскости, то для таких квадратур справедливы мажорантные оценки точности Трефетена и Вайдемана [7], см. также [8–15]. В [16, 17] построено обобщение оценок Трефетена и Вайдемана на случай, когда ближайший полюс подынтегральной функции является кратным.

В данной работе построены новые оценки погрешности экспоненциально сходящихся квадратур от периодических функций по полному периоду. Подынтегральная функция может иметь произвольное число полюсов целого порядка на комплексной плоскости. Если сетка достаточно подробная, то есть разрешает профиль подынтегральной функции, то предлагаемые оценки являются не мажорантными, а асимптотически точными.

Экстраполируя, т.е. исключая эту погрешность из численной квадратуры, можно вычислять интегралы указанных классов с точностью ошибок округления уже на чрезвычайно грубых сетках, содержащих всего ~10 шагов.

ЭКСПОНЕНЦИАЛЬНО СХОДЯЩИЕСЯ КВАДРАТУРЫ

Один из классов экспоненциально сходящихся квадратур – это интегралы от периодических функций по полному периоду. Заменой $z = {{e}^{{{{2\pi ix} \mathord{\left/ {\vphantom {{2\pi ix} X}} \right. \kern-0em} X}}}}$ перейдем от интеграла по периоду $[0,X]$ к интегралу по единичной окружности $\left| z \right| = 1$ на комплексной плоскости. Обход этого контура будем выполнять против часовой стрелки. В работе [7] была сформулирована и доказана следующая теорема.

Теорема 1

Пусть $u(z)$ аналитическая в кольце ${{R}^{{ - 1}}} < \left| z \right| < R,$ где $R > 1,$ причем $\left| {u(z)} \right| \leqslant {{M}_{0}}.$ Введем на единичной окружности равномерную сетку ${{z}_{n}} = {{\exp (2\pi in} \mathord{\left/ {\vphantom {{\exp (2\pi in} N}} \right. \kern-0em} N}),$ $n = \overline {0,N} .$ Рассмотрим интеграл и квадратурную формулу трапеций

(1)
$I = \oint\limits_{\left| z \right| = 1} {u(z)\frac{{dz}}{{iz}}} ,\,\,\,\,{{I}_{N}} = \frac{{2\pi }}{N}\sum\limits_{n = 1}^N {u({{z}_{n}}).} $

Тогда для погрешности квадратуры верна оценка

(2)
$\delta = \left| {I - {{I}_{N}}} \right| \leqslant \frac{{4\pi {{M}_{0}}}}{{{{R}^{N}} - 1}}.$

Очевидно, что теорема 1 заменой $z = {{e}^{{ix}}}$ сводится к аналогичной, но интегрирование будет проходить уже по полному периоду функции $u({{e}^{{ix}}})$ на вещественной оси.

В работах [16, 17] было показано, что зависимость оценки (2) от $N$ может быть не мажорантной, а асимптотически точной. Такая ситуация реализуется, если $u(z)$ имеет только особенности типа полюсов первого порядка, а $R$ взято таким образом, что ближайшая к единичной окружности особенность лежит на границе кольца ${{R}^{{ - 1}}} < \left| z \right| < R.$ При этом подынтегральная функция неограниченно возрастает, если приближаться к особенности изнутри кольца. Таким образом, константа ${{M}_{0}}$ теряет свой привычный смысл из теоремы 1. Мы тщательно проанализировали метод доказательства теоремы 1, приведенный в [7] и обнаружили возможность существенного усиления результатов данной теоремы, при некоторых дополнительных условиях на подынтегральную функцию.

ВЫЧИСЛЕНИЕ ПОГРЕШНОСТИ

Рассмотрим подробно контурный интеграл по единичной окружности от функции, которая имеет один простой полюс внутри нее и еще один простой полюс вне. Этот случай соответствует интегралу, рассмотренному в [7]. Пусть точка ${{a}_{1}}$ лежит внутри, а точка ${{a}_{2}}$ снаружи $\left| z \right| = 1$ и, функция $u(z)$ аналитична в кольце ${{R}^{{ - 1}}} < \left| z \right| < R$ с $R = \min \left\{ {{1 \mathord{\left/ {\vphantom {1 {\left| {{{a}_{1}}} \right|}}} \right. \kern-0em} {\left| {{{a}_{1}}} \right|}},\left| {{{a}_{2}}} \right|} \right\}.$ Тогда интеграл имеет вид

(3)
$G = \oint\limits_{\left| z \right| = 1} {g(z)dz} = \oint\limits_{\left| z \right| = 1} {\frac{{u(z)dz}}{{(z - {{a}_{1}})(z - {{a}_{2}})}}} = 2\pi i\frac{{u({{a}_{1}})}}{{({{a}_{1}} - {{a}_{2}})}}.$

Сделаем одно предположение ради упрощения выкладок. Оно слабо повлияет на результат. Пусть $u(z) = 1,$ тогда подынтегральную функцию перепишем в таком виде

(4)
$\begin{gathered} g(z) = \frac{1}{{(z - {{a}_{1}})(z - {{a}_{2}})}} = \\ = \,\,\frac{1}{{({{a}_{1}} - {{a}_{2}})(z - {{a}_{1}})}} + \frac{1}{{({{a}_{2}} - {{a}_{1}})(z - {{a}_{2}})}}. \\ \end{gathered} $

Теперь разложим каждую дробь в ряд Лорана как сумму геометрической прогрессии

(5)
$\begin{gathered} g(z) = \frac{1}{{({{a}_{1}} - {{a}_{2}})(z - {{a}_{1}})}} + \frac{1}{{({{a}_{2}} - {{a}_{1}})(z - {{a}_{2}})}} = \\ = \frac{1}{{({{a}_{1}} - {{a}_{2}})}}\sum\limits_{{{k}_{1}} = 0}^\infty {\frac{{a_{1}^{{{{k}_{1}}}}}}{{{{z}^{{{{k}_{1}} + 1}}}}}} - \frac{1}{{({{a}_{2}} - {{a}_{1}})}}\sum\limits_{{{k}_{1}} = 0}^\infty {\frac{{{{z}^{{{{k}_{2}}}}}}}{{a_{2}^{{{{k}_{2}} + 1}}}}} . \\ \end{gathered} $

Будем пользоваться сеткой ${{z}_{n}},$ $n = \overline {0,N} ,$ которая введена в теореме 1. Получим явное выражение для шага сетки $\Delta {{z}_{n}} = {{z}_{{n + 1}}} - {{z}_{n}}$

(6)
$\begin{gathered} \Delta {{z}_{n}} = \exp \left( {\frac{{2\pi i\left( {n + 1} \right)}}{N}} \right) - \exp \left( {\frac{{2\pi in}}{N}} \right) = \\ = {{z}_{n}}\left( {\exp \left( {\frac{{2\pi i}}{N}} \right) - 1} \right)\mathop = \limits_{N \to \infty } {{z}_{n}}\left( {\frac{{2\pi i}}{N} + O\left( {\frac{1}{{{{N}^{2}}}}} \right)} \right). \\ \end{gathered} $

Отбрасывая член $O({{N}^{{ - 2}}})$ в выражении для шага сетки, запишем квадратурную формулу “трапеций” в следующем виде

(7)
${{G}_{N}} = \sum\limits_{n = 0}^{N - 1} {g({{z}_{n}})\Delta {{z}_{n}}} = \frac{{2\pi i}}{N}\sum\limits_{n = 0}^{N - 1} {g({{z}_{n}}){{z}_{n}}} .$

Подставим представление $g\left( {{{z}_{n}}} \right)$ в виде суммы рядов в квадратурную формулу, затем поменяем местами ряды и конечную сумму. Последнее действие допустимо в силу абсолютной сходимости полученного двойного числового ряда (каждый член двойного ряда из модулей можно ограничить соответствующим членом бесконечно убывающей геометрической прогрессии, которая имеет конечную сумму). Получается следующее выражение для квадратурной формулы

(8)
${{G}_{N}} = \frac{{2\pi i}}{{N({{a}_{1}} - {{a}_{2}})}}\left[ {\sum\limits_{{{s}_{1}} = 0}^\infty {\sum\limits_{n = 0}^{N - 1} {\frac{{a_{1}^{{{{s}_{1}}}}}}{{z_{n}^{{{{s}_{1}}}}}}} } + \sum\limits_{{{s}_{2}} = 0}^\infty {\sum\limits_{n = 0}^{N - 1} {\frac{{z_{n}^{{{{s}_{2}} + 1}}}}{{a_{2}^{{{{s}_{2}} + 1}}}}} } } \right].$

Для проведения преобразований нам потребуется следующий известный результат

(9)
$\sum\limits_{n = 0}^{N - 1} {\exp \left( { \pm 2\pi i\frac{{nk}}{N}} \right)} = \left\{ {\begin{array}{*{20}{l}} {N,\,\,k\,\,{\text{кратно}}\,\,N} \\ {0,\,\,{\text{иначе}}} \end{array}} \right..$

Преобразуем вторую сумму в квадратных скобках в формуле (8)

(10)
$\begin{gathered} \sum\limits_{{{s}_{2}} = 0}^\infty {\sum\limits_{n = 0}^{N - 1} {\frac{{z_{n}^{{{{s}_{2}} + 1}}}}{{a_{2}^{{{{s}_{2}} + 1}}}}} } = \left\{ {\begin{array}{*{20}{l}} {\left( {{{s}_{2}} + 1} \right)\,\,{\text{кратно}}\,\,N} \\ {\left( {{{s}_{2}} + 1} \right) = N{{p}_{2}},\,\,{{p}_{2}} = \overline {1,\infty } } \end{array}} \right\} = \\ = N\sum\limits_{{{p}_{2}} = 1}^\infty {\frac{1}{{a_{2}^{{N{{p}_{2}}}}}} = N\frac{{{1 \mathord{\left/ {\vphantom {1 {a_{2}^{N}}}} \right. \kern-0em} {a_{2}^{N}}}}}{{1 - {1 \mathord{\left/ {\vphantom {1 {a_{2}^{N}}}} \right. \kern-0em} {a_{2}^{N}}}}}} . \\ \end{gathered} $

Преобразуем первую сумму в (8)

(11)
$\begin{gathered} \sum\limits_{{{s}_{1}} = 0}^\infty {\sum\limits_{n = 0}^{N - 1} {\frac{{a_{1}^{{{{s}_{1}}}}}}{{z_{n}^{{{{s}_{1}}}}}}} } = \left\{ {\begin{array}{*{20}{l}} {{{s}_{1}}\,\,{\text{кратно}}\,\,N} \\ {{{s}_{1}} = N{{p}_{1}},\,\,{{p}_{1}} = \overline {0,\infty } } \end{array}} \right\} = \\ = \,\,N\sum\limits_{{{p}_{1}} = 0}^\infty {a_{1}^{{N{{p}_{1}}}} = N\frac{1}{{1 - a_{1}^{N}}}} . \\ \end{gathered} $

Получаем

(12)
$\begin{gathered} {{G}_{n}} = \frac{{2\pi i}}{{N\left( {{{a}_{1}} - {{a}_{2}}} \right)}}\left[ {N\left( {\frac{1}{{1 - a_{1}^{N}}} + \frac{1}{{a_{2}^{N} - 1}}} \right)} \right] = \\ = \frac{{2\pi i}}{{\left( {{{a}_{1}} - {{a}_{2}}} \right)}}\left[ {\frac{1}{{1 - a_{1}^{N}}} + \frac{1}{{a_{2}^{N} - 1}}} \right]. \\ \end{gathered} $

Наконец$,$ вычислим погрешность

(13)
$\begin{gathered} {{\Delta }_{N}} = G - {{G}_{N}} = \\ = 2\pi i\left( {\frac{1}{{\left( {{{a}_{1}} - {{a}_{2}}} \right)}}\left( {1 - \frac{1}{{1 - a_{1}^{N}}}} \right) + \frac{1}{{\left( {{{a}_{2}} - {{a}_{1}}} \right)}}\left( {\frac{1}{{a_{2}^{N} - 1}}} \right)} \right). \\ \end{gathered} $

Полученный результат легко обобщить на случай, когда функция $u\left( z \right)$ не равна тождественно единице. Это требует более громоздких выкладок, которые мы здесь не приводим. Справедлива другая теорема.

Теорема 2

Пусть точка $z = {{a}_{1}}$ лежит внутри единичной окружности, а точка $z = {{a}_{2}}$ – вне ее. Пусть функция $u(z)$ аналитична на всей комплексной плоскости за исключением, быть может, бесконечно удаленной точки и не обращается в нуль в точках $z = {{a}_{{1,2}}}.$ Тогда квадратура трапеций для интеграла $G$ имеет точность

(14)
$\begin{gathered} {{\Delta }_{N}} = G - {{G}_{N}} = \\ = 2\pi i\left( {\frac{{u\left( {{{a}_{1}}} \right)}}{{\left( {{{a}_{1}} - {{a}_{2}}} \right)}}\left( {1 - \frac{1}{{1 - a_{1}^{N}}}} \right) + \frac{{u\left( {{{a}_{2}}} \right)}}{{\left( {{{a}_{2}} - {{a}_{1}}} \right)}}\left( {\frac{1}{{a_{2}^{N} - 1}}} \right)} \right). \\ \end{gathered} $

Оценка (14) является не мажорантной, а асимптотически точной. Единственное приближение, которое было сделано, содержится в приближенном выражении для шага (6).

АПРОБАЦИЯ ОЦЕНКИ

Были проведены расчеты с тестовым интегралом, имеющим известное точное значение

(15)
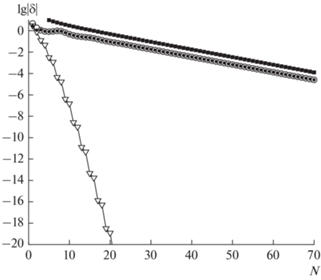
$J = \oint\limits_{\left| z \right| = 1} {\frac{{\sin \left( z \right)}}{{\left( {z - {{a}_{1}}} \right)\left( {z - {{a}_{2}}} \right)}}dz} = 2\pi i\frac{{\sin \left( {{{a}_{1}}} \right)}}{{\left( {{{a}_{1}} - {{a}_{2}}} \right)}},$
где ${{a}_{1}} = 0.6 + 0.6i$ и ${{a}_{2}} = 2 - i.$ В данном случае ${1 \mathord{\left/ {\vphantom {1 {\left| {{{a}_{1}}} \right|}}} \right. \kern-0em} {\left| {{{a}_{1}}} \right|}} \approx 1.2$ и $\left| {{{a}_{2}}} \right| \approx 2.2,$ поэтому $R$ из теоремы 1 равняется ${1 \mathord{\left/ {\vphantom {1 {\left| {{{a}_{1}}} \right|}}} \right. \kern-0em} {\left| {{{a}_{1}}} \right|}}.$ В ходе расчетов была получена фактическая погрешность, вычислялась оценка Трефетена–Вайдемана (2), наша оценка (14) и погрешность после экстраполяции.

По этим данным на рис. 1 был построен график сходимости в полулогарифмическом масштабе. Здесь черные точки обозначают фактическую погрешность, белые кружки обозначают нашу оценку, а черные квадраты обозначают оценку Трефетена–Вайдемана с константой ${{M}_{0}} = 1.$ Напомним, что эта константа теряет свой смысл из теоремы 1, если на границе кольца лежит особенность, поэтому мы взяли ее единичной.

Рис. 1.

График сходимости формулы трапеций. Обозначения см. в тексте.

Из графика видно, что наша оценка совпадает с фактической погрешностью уже при $N > 4.$ Оценка Трефетена–Вайдемана не передает начальный участок кривой. Она описывает кривую начиная с $N \cong 15.$ Эта оценка асимптотически точна по N, но истинное значение константы ${{M}_{0}}$ неизвестно. Поэтому оценка Трефетена–Вайдемана не может использоваться для экстраполяции. Таким образом, оценка точности, построенная в данной работе, намного сильнее оценки Трефетена–Вайдемана.

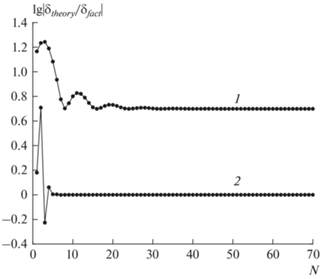
Данные выводы подтверждаются и графиком на рис. 2. Здесь построена зависимость отношения оценок погрешности к фактической точности. Цифрой 1 обозначен график отношения оценки Трефетена–Вайдемана к фактической точности, а цифрой 2 отношение нашей оценки к тому же. Видно, что при $N > 4$ наша оценка практически неотличима от фактической погрешности. Поэтому ее можно исключить из квадратуры, то есть провести экстраполяцию. Это кардинально повышает точность расчета. Видно также, что оценка Трефетена–Вайдемана заметно хуже передает зависимость погрешности от числа узлов: соответствующее отношение выходит на константу на существенно более подробных сетках, чем оценка (14).

Рис. 2.

Отношение теоретических оценок (2) и (14) для интеграла (15) к фактической точности. Обозначения см. в тексте.

ЭКСТРАПОЛЯЦИЯ ПОГРЕШНОСТИ

Исключим погрешность (14) из рассчитанной квадратуры по формуле

(16)
${{\tilde {G}}_{N}} = {{G}_{N}} + {{\Delta }_{N}}.$

Это эквивалентно введению некоторой новой квадратурной формулы. Ее погрешность показана на рис. 1 белыми треугольниками. Видно, что скорость сходимости квадратуры (16) кардинально превосходит даже экспоненциальную. Точность порядка ошибок единичного округления достигается уже при $N\sim 15,$ что в ~10 раз меньше, чем для формулы трапеций. Трудоемкость такого расчета сопоставима с трудоемкостью явных формул. Данный подход кардинально превосходит мировой уровень.

ЗАКЛЮЧЕНИЕ

Изложенный метод является мощным инструментарием для решения физических задач. Если удается найти преобразования переменных, сводящие интегралы к рассмотренному типу, то вычисления ускоряются в тысячи раз.

В данной работе 1) построена принципиально новая оценка точности квадратуры трапеций, которая является асимптотически точной. 2) Предложена процедура экстраполяции, обеспечивающая расчет квадратуры с точностью ошибок единичного округления уже на очень грубых сетках с числом шагов 5–15.

Исследование выполнено при поддержке Российского научного фонда (проект № 20-71-00097).

Список литературы

  1. Дубинов А.Е., Дубинова И.Д., Сайков С.К. W-функция Ламберта и ее применение в математических задачах физики: Учеб. пособие для вузов. Саров: ФГУП “РФЯЦ-ВНИИЭФ”, 2006. С. 160.

  2. Al Kafri H., Jeffrey D.J., Corless R.M. // Lect. Notes Comput. Sci. 2017. V. 10693. P. 270.

  3. Ooura T. // Publ. Res. Inst. Math. Sci. 2005. V. 41. No. 4. P. 971.

  4. Ooura T., Mori M. // J. Comput. Appl. Math. 1999. V. 112. No. 1–2. P. 229.

  5. Ooura T., Mori M. // J. Comput. Appl. Math. 1991. V. 38. P. 353.

  6. Weideman J.A.C., Trefethen L.N. // Math. Comput. 2007. V. 76. No. 259. P. 1341.

  7. Trefethen L.N., Weideman J.A.C. // SIAM Rev. 2014. V. 56. No. 3. P. 385.

  8. Javed M., Trefethen L.N. // Proc. Royal. Soc. A. 2014. V. 470. No. 2161. Art. No. 20130571.

  9. Weideman J.A.C. // The Amer. Math. Month. 2002. V. 109. No. 1. P. 21.

  10. Eggert N. Lund J. // J. Comput. Appl. Math. 1989. V. 27. No. 3. P. 389.

  11. Waldvogel J. // Springer Optim. Appl. 2010. V. 42. P. 267.

  12. Goodwin E.T. // Math. Proc. Camb. Phil. Soc. 1949. V. 45. No. 2. P. 241.

  13. Kalitkin N.N., Kolganov S.A. // Dokl. Math. 2017. V. 95. No. 2. P. 157.

  14. Kalitkin N.N., Kolganov S.A. // Math. Models Comp. Simul. 2017. V. 9. No. 5. P. 554.

  15. Kalitkin N.N., Kolganov S.A. // Math. Models Comp. Simul. 2018. V. 10. No. 4. P. 472.

  16. Белов А.А., Калиткин Н.Н., Хохлачев В.С. // Препринт ИПМ им. М.В. Келдыша. 2020. № 75. 24 с.

  17. Хохлачев В.С., Белов А.А., Калиткин Н.Н. // Изв. РАН. Сер. физ. 2021. Т. 85. № 2. С. 282.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал