1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 7, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 7, стр. 1042-1046

Влияние параметра порядка на динамику предельно короткого импульса в оптически анизотропной среде с углеродными нанотрубками

Н. Н. Конобеева 1, *, М. Б. Белоненко 1

1 Федеральное государственное автономное образовательное учреждение высшего образования “Волгоградский государственный университет”
Волгоград, Россия

* E-mail: yana_nn@volsu.ru

Поступила в редакцию 14.02.2022
После доработки 28.02.2022
Принята к публикации 23.03.2022

Полный текст (PDF)

Аннотация

Исследовано влияние параметра порядка на динамику трехмерного предельно короткого оптического импульса в нелинейной анизотропной оптической среде, содержащей углеродные нанотрубки. Исследована зависимость формы трехмерного предельно короткого оптического импульса от расстояния от точки фазового перехода и угла между электрическим полем импульса и осью углеродных нанотрубок.

ВВЕДЕНИЕ

В последние годы наблюдается повышенный интерес исследователей к изучению нелинейных сред, испытывающих фазовый переход. Общая характеристика фазового перехода состоит в том, что он либо включает в себя разрыв параметра порядка согласно парадигме фазовых переходов Ландау [1, 2], либо изменение топологического инварианта [3, 4]. Определение характеристик и контроль различных фаз – одна из важных задач физики конденсированного состояния и материаловедения. В частности, изучение фазовых переходов в двумерных системах сыграло решающую роль в понимании механизмов фазовых переходов [5–7]. К двумерным системам можно отнести и углеродные нанотрубки (УНТ), которые обладают уникальными нелинейными свойствами [8, 9] и способны выдерживать электрические поля большой напряженности. С этой точки зрения важной практической задачей является изучение неравновесной динамики параметра порядка в присутствии внешних переменных полей. С другой стороны, хорошо известно, что среды с УНТ оказывают стабилизирующий эффект на распространяющиеся в них локализованные электромагнитные волны, т. н. световые пули [10, 11]. Это свойство делает возможным применять УНТ для исследования спектра среды и внутренней динамики. Ранее нами были изучены особенности распространения предельно коротких импульсах в средах со скалярным [12] и векторным [13] параметром порядка. При этом не учитывалась оптическая анизотропия среды. Рассмотрим распространение электромагнитных волн в диэлектрическом кристалле, ось которого не сонаправлена оси УНТ, что связано с необходимостью учесть вторую компоненту электрического поля.

МОДЕЛЬ И ОСНОВНЫЕ УРАВНЕНИЯ

Рассмотрим влияние скалярного параметра порядка в среде с УНТ. Для описания динамики изучаемой системы воспользуемся уравнением движения, которое следует из теории фазовых переходов [14, 15]:

(1)
$\frac{{dP}}{{dt}} = - {\text{Г}}\frac{{\delta {\text{Ф}}}}{{\delta {\text{P}}}},$
где ${\text{Г}} = {\text{1}}$ – кинетический коэффициент, Р – параметр порядка, Ф – плотность функционала свободной энергии. Параметр порядка позволяет описывать системы с различными физическими свойствами. Это могут быть сегнетоэлектрики, ферромагнетики и т.д. В роли параметра порядка в этом случае будет выступать поляризация, намагниченность и другие характеристики [15]. Использование подходов Паташинского и Покровского позволяет описать с помощью одного уравнения различные по свойствам системы. Рассмотрим в качестве параметра поляризацию электрического поля, направленного вдоль оси нанотрубок.

Плотность функционала свободной энергии зададим в виде:

(2)
$\Phi = {{\Phi }_{0}} + \rho {{P}^{2}} + \beta {{P}^{4}} + \chi EP.$

При этом необходимо учесть, что электроны в УНТ будут находится под действием как электромагнитного поля самого импульса, так и поля среды:

(3)
${{E}_{s}} = \frac{{\delta \Phi }}{{\delta P}}.$

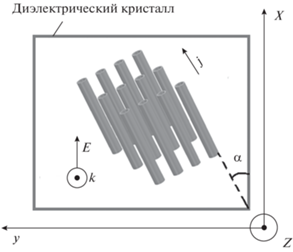
Определим геометрию задачи следующим образом. Оси OX, OY и OZ сонаправлены осям кристалла. Ось УНТ лежит в плоскости XOY и образует с осью OX угол α (рис. 1). Для простоты задачи выберем направления электрического поля вдоль оси кристалла OX.

Рис. 1.

Схематичное изображение геометрии задачи.

Векторный потенциал зададим в виде: $\vec {A} = \left( {{{A}_{x}}\left( {x,y,z,t} \right),{{A}_{y}}\left( {x,y,z,t} \right),0} \right),$ тогда плотность электрического тока будет иметь вид: $\vec {j} = \left( {{{j}_{x}}\left( {x,y,z,t} \right),{{j}_{y}}\left( {x,y,z,t} \right),0} \right).$

Запишем трехмерное волновое уравнение для компоненты электрического поля, направленной под углом к оси УНТ в виде:

(4)
$\frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{t}^{2}}}} = \frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{z}^{2}}}} + \frac{{4\pi }}{c}\vec {j}\left( {\vec {A}} \right),$
где c – скорость света.

Переходя в цилиндрическую систему координат, перепишем уравнение (4) для двух компонент (x, y) поля:

(5)
$\begin{gathered} \frac{1}{{\nu _{o}^{2}}}\frac{{{{\partial }^{2}}{{A}_{x}}}}{{\partial {{t}^{2}}}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{A}_{x}}}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}{{A}_{x}}}}{{\partial {{z}^{2}}}} + \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}{{A}_{x}}}}{{\partial {{\phi }^{2}}}} + \frac{{4\pi }}{c}{{j}_{x}}\left( {{{A}_{x}}} \right), \\ \frac{1}{{\nu _{e}^{2}}}\frac{{{{\partial }^{2}}{{A}_{y}}}}{{\partial {{t}^{2}}}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{A}_{y}}}}{{\partial r}}} \right) + \\ + \,\,\frac{{{{\partial }^{2}}{{A}_{y}}}}{{\partial {{z}^{2}}}} + \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}{{A}_{y}}}}{{\partial {{\phi }^{2}}}} + \frac{{4\pi }}{c}{{j}_{y}}\left( {{{A}_{y}}} \right), \\ {{\nu }_{o}} = {c \mathord{\left/ {\vphantom {c {{{n}_{x}}}}} \right. \kern-0em} {{{n}_{x}}}},\,\,\,\,{{\nu }_{e}} = {c \mathord{\left/ {\vphantom {c {{{n}_{y}}}}} \right. \kern-0em} {{{n}_{y}}}}, \\ \end{gathered} $
где r, z, φ – координаты в цилиндрической системе, nx, ny – показатели преломления в направлении x и y соответственно.

Учтем, что закон дисперсии электронов зигзаг УНТ имеет вид [16]:

(6)
${{\varepsilon }_{s}}\left( p \right) = \pm \gamma \sqrt {1 + 4{\text{cos}}\left( {ap} \right){\text{cos}}\left( {\frac{{\pi s}}{m}} \right) + 4{\text{co}}{{{\text{s}}}^{2}}\left( {\frac{{\pi s}}{m}} \right)} ,$
где $s = 1,2...m,$ нанотрубка имеет тип $(m,0),$ $\gamma \approx 2.7$ эВ, $a = {{3b} \mathord{\left/ {\vphantom {{3b} {2\hbar }}} \right. \kern-0em} {2\hbar }},$ $b = 0.142$ нм – межатомное расстояние в графеноподобных структурах.

Проводя вычисления аналогично [10], запишем выражение для плотности тока:

(7)
$\begin{gathered} {{j}_{0}} = - e{{n}_{0}}\sum\limits_k {{{D}_{k}}\sin \left( {\frac{{ke}}{c}A\left( t \right)} \right)} , \\ {{D}_{k}} = \sum\limits_{s = 1}^m {\int\limits_{ - {\pi \mathord{\left/ {\vphantom {\pi a}} \right. \kern-0em} a}}^{{\pi \mathord{\left/ {\vphantom {\pi a}} \right. \kern-0em} a}} {dp{\kern 1pt} '} } {{A}_{{ks}}}\cos \left( {kp{\kern 1pt} '} \right)\frac{{\exp \left( { - {{{{\varepsilon }_{s}}\left( {p{\kern 1pt} '} \right)} \mathord{\left/ {\vphantom {{{{\varepsilon }_{s}}\left( {p{\kern 1pt} '} \right)} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right)}}{{1 + \exp \left( { - {{{{\varepsilon }_{s}}\left( {p{\kern 1pt} '} \right)} \mathord{\left/ {\vphantom {{{{\varepsilon }_{s}}\left( {p{\kern 1pt} '} \right)} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right)}}, \\ \end{gathered} $
где ${{n}_{0}}$ – концентрация электронов в УНТ, ${{k}_{B}} = 1.38 \cdot {{10}^{{ - 23}}}$ Дж/К, Т – температура, Aks – коэффициенты разложения скорости электронов в ряд Фурье.

С учетом формулы (7) система уравнений (5) может быть представлена в виде:

(8)
$\begin{gathered} \left\{ \begin{gathered} \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{A}_{x}}}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}{{A}_{x}}}}{{\partial {{z}^{2}}}} - \frac{1}{{v_{o}^{2}}}\frac{{{{\partial }^{2}}{{A}_{x}}}}{{\partial {{t}^{2}}}} + \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}{{A}_{x}}}}{{\partial {{\varphi }^{2}}}} + \hfill \\ + \,\,g\,{\text{cos}}\,\alpha \sum\limits_{k = 1}^\infty {{{D}_{k}}{\text{sin}}\left( {{{C}_{k}}\left( {{{A}_{x}},{{A}_{y}}} \right) + \frac{{aek{{A}_{s}}}}{c}} \right)} = 0 \hfill \\ \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{A}_{y}}}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}{{A}_{y}}}}{{\partial {{z}^{2}}}} - \frac{1}{{v_{e}^{2}}}\frac{{{{\partial }^{2}}{{A}_{y}}}}{{\partial {{t}^{2}}}} + \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}{{A}_{y}}}}{{\partial {{\varphi }^{2}}}} + \hfill \\ + \,\,g\,{\text{sin}}\,\alpha \sum\limits_{k = 1}^\infty {{{D}_{k}}{\text{sin}}\left( {{{C}_{k}}\left( {{{A}_{x}},{{A}_{y}}} \right)} \right)} = 0 \hfill \\ \end{gathered} \right. \\ {{C}_{k}}\left( {{{A}_{x}},{{A}_{y}}} \right) = \frac{{aek\left( {{{A}_{x}}\,{\text{cos}}\,\alpha + {{A}_{y}}\,{\text{sin}}\,\alpha } \right)}}{c},\,\,\,\,g = \frac{{4e{{n}_{0}}{{\gamma }_{0}}a}}{c}. \\ \end{gathered} $
Здесь (Ax, Ay) соответствуют компонентам электрического поля предельно короткого импульса, ${{A}_{s}}$ – электрическому полю среды:${{E}_{s}} = - {{c}^{{ - 1}}}{{\partial {{A}_{s}}} \mathord{\left/ {\vphantom {{\partial {{A}_{s}}} {\partial t}}} \right. \kern-0em} {\partial t}}$ (3).

В дальнейшем рассмотрении не будем учитывать производную по углу в силу цилиндрической симметрии, а также пренебрежем накоплением заряда в массиве УНТ вследствие неоднородности поля импульса [17].

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Исследуемые уравнения (8) решались численно [18] при следующих параметрах системы: УНТ типа zigzag (13, 0), коэффициенты Dk вычислялись при T = 293 K. Время релаксации в УНТ trel ≈ ≈ 10–11 c, длительность импульса tpulse = 2 · 10–14 c, таким образом tpulse $ \ll $ trel.

Начальное условие выбиралось в виде:

(9)
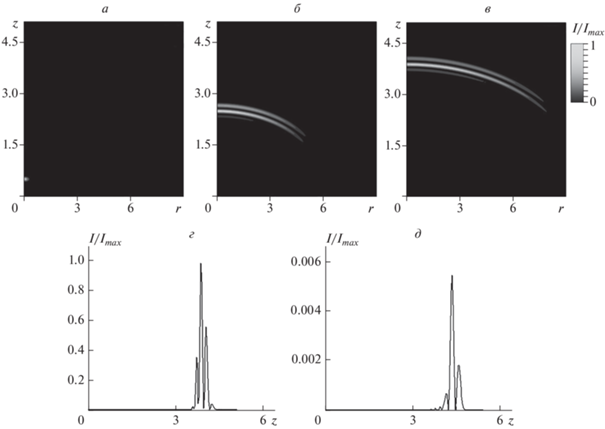
$\begin{gathered} {{A}_{x}}\left( {r,z,0} \right) = Q\,{\text{exp}}\left( { - \frac{{{{{\left( {z - {{z}_{0}}} \right)}}^{2}}}}{{l_{z}^{2}}}} \right){\text{exp}}\left( { - \frac{{{{{\left( {r - {{r}_{0}}} \right)}}^{2}}}}{{l_{r}^{2}}}} \right), \\ \frac{{d{{A}_{x}}\left( {r,z{\text{,}}0} \right)}}{{dt}} = \\ = 2{{\upsilon }_{0}}\frac{{\left( {z - {{z}_{0}}} \right)}}{{l_{r}^{2}}}Q\,{\text{exp}}\left( { - \frac{{{{{\left( {z - {{z}_{0}}} \right)}}^{2}}}}{{l_{z}^{2}}}} \right){\text{exp}}\left( { - \frac{{{{{\left( {r - {{r}_{0}}} \right)}}^{2}}}}{{l_{r}^{2}}}} \right), \\ {{A}_{y}}\left( {r,z,0} \right) = 0,\,\,\,\,\frac{{d{{A}_{y}}\left( {r,z,0} \right)}}{{dt}} = 0, \\ \Phi \left( {r,z,0} \right) = \sqrt {\left| {\frac{{2\rho }}{\beta }} \right|} ,\,\,\,\,r = \sqrt {{{x}^{2}} + {{y}^{2}}} ,\,\,\,\,{\text{tg}}\,\varphi = \frac{y}{x}, \\ \end{gathered} $
где Q – амплитуда электромагнитного импульса на входе в среду с УНТ, ${{l}_{z}},{{l}_{r}}$ – определяют ширину импульса вдоль направлений z и r соответственно, $\left( {{{r}_{0}},\,{{z}_{0}}} \right)$ – начальная координата центра импульса, ${{\upsilon }_{0}}$ – начальная скорость импульса.

Эволюционная картина для электромагнитного поля при движении импульса в анизотропной среде с УНТ показана на рис. 2. Из рис. 2а–2в видно, что импульс, распространяющийся в анизотропной оптической среде, претерпевает дисперсионное уширение. При этом наблюдается ограниченная область пространства, в которой сосредоточена большая часть энергии предельно короткого импульса. Поэтому можно говорить об устойчивом характере распространения электромагнитного поля в образце. Следует отметить, что интенсивность импульса при этом уменьшается. Это связано с взаимодействием возникающего в углеродных нанотрубках тока с подсистемой, описываемой параметром порядка. Релаксационный характер динамики этой подсистемы вызывает уменьшение электрического поля импульса. Рисунки 2г–2д демонстрируют, что вторая компонента электрического поля Ey примерно в 100 раз меньше по амплитуде, чем компонента поля Ex, и на дальнейших рисунках она не показана. Однако следует отметить, что наличие второй компоненты приводит к более значительному уширению импульса, чем в ранее рассмотренных задачах.

Рис. 2.

Интенсивность трехмерного электромагнитного импульса $I\left( {r,z,t} \right) = E_{x}^{2}\left( {r,z,t} \right)$ в различные моменты времени (ρ = 0.2, β = –1, α = 0.6 рад): исходная форма импульса (а); t = 6 (б); 10 отн. ед. (в). Рисунки (г) и (д) – продольные сечения при t = 10 отн. ед.: для Ex- (г) и Ey- (д) компоненты электрического поля. Imax – максимальное значение интенсивности.

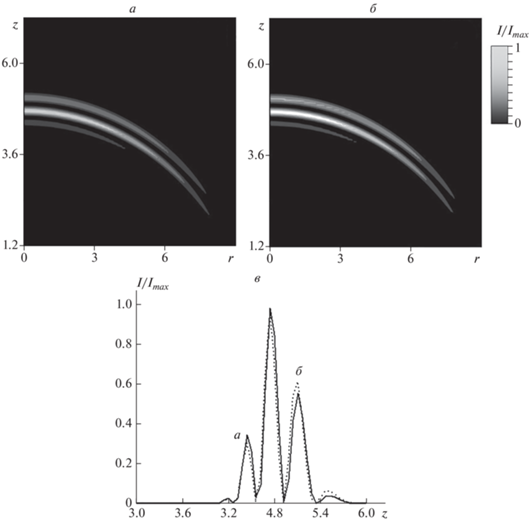
Зависимость формы импульса от параметра порядка (величины ρ) показана на рис. 3. Отметим, что параметр ρ в рамках теории фазовых переходов определяет удаление от точки фазового перехода и пропорционален величине отклонения текущей температуры от температуры, характерной для фазового перехода. Приведенные зависимости позволяют сделать вывод, что для определения точки фазового перехода может служить предельно короткий импульс, а точнее его форма.

Рис. 3.

Интенсивность трехмерного электромагнитного импульса $I\left( {r,z,t} \right) = E_{x}^{2}\left( {r,z,t} \right)$ для разных значений параметра ρ (для момента времени, t = 10 отн. ед., α = 0.9 рад): ρ = 0.1 (а); 0.6 (б); срезы для рис. 3а и 3б при r = 0 (в). Imax – максимальное значение интенсивности.

Дополнительно была проанализирована зависимость импульса от угла α между УНТ и осью кристалла. Показано, что значение α не оказывает существенного влияния на форму импульса.

ЗАКЛЮЧЕНИЕ

Получено эффективное уравнение для описания динамики трехмерных предельно коротких оптических импульсов в анизотропной оптической среде, содержащей углеродные нанотрубки, с учетом параметра порядка. Обнаружено, что амплитуда импульса уменьшается со временем. Это связано как с релаксационной динамикой параметра порядка, так и с наличием второй компоненты поля Ey, которая учитывается за счет анизотропии. Динамика предельно короткого импульса позволяет определять расстояние от точки фазового перехода в анизотропной оптической среде с углеродными нанотрубками.

Работа выполнена при поддержке Минобрнауки РФ и Совета по грантам Президента РФ (проект № MД-3173.2021.1.2).

Список литературы

  1. Ма Ш. Современная теория критических явлений. М.: Мир, 1980. 296 с.

  2. Christian J.W. The theory of transformations in metals and alloys. Oxford: Pergamon, 2002. 1200 p.

  3. Sachdev S. Quantum phase transitions. Cambridge: Cambridge University Press, 2011, 478 p.

  4. Fradkin E. Field theories of condensed matter physics. Cambridge: Cambridge University Press, 2013. 838 p.

  5. Wang Y., Xiao J., Zhu H. et al. // Nature. 2017. V. 550. P. 487.

  6. Rehn D.A., Li Y., Pop E. et al. // NPJ Comput. Mater. 2018. V. 4. Art. No. 2.

  7. Duerloo K.-A.N., Reed E.J. // ACS Nano. 2015. V. 10. P. 289.

  8. Vinogradov G.A., Astakhova T.Yu., Gurin O.D. et al. Abstracts of invited lectures and contributed papers “Fullerenes and Atomic Clusters”. St. Petersburg, 1999. P. 189.

  9. Astakhova T.Yu., Gurin O.D., Menon M. et al. // Phys. Rev. B. 2001. V. 64. Art. No. 035418.

  10. Белоненко М.Б., Лебедев Н.Г., Попов А.С. // Письма в ЖЭТФ. 2010. Т. 91. № 9. С. 506; Belonenko M.B., Lebedev N.G., Popov A.S. // JETP Lett. 2010. V. 91. No. 9. P. 461.

  11. Белоненко М.Б., Глазов С.Ю., Лебедев Н.Г. и др. // ФТТ. 2009. Т. 51. № 8. С. 1657; Belonenko M.B., Glazov S.Y., Lebedev N.G. et al. // Phys. Solid State. 2009. V. 51. No. 8. P. 1758.

  12. Zhukov A.V., Bouffanais R., Konobeeva N.N. et al. // J. Appl. Phys. 2017. V. 121. No. 8. Art. No. 084301.

  13. Konobeeva N.N., Belonenko M.B. // J. Nano-Electron. Phys. 2020. V. 12. No. 4. Art. No. 04016.

  14. Ландау Л.Д., Лифшиц Е.М. Статистическая физика. М.: Физматлит, 2002. 616 с.

  15. Паташинский А.З., Покровский В.Л. Флуктуационная теория фазовых переходов. М.: Наука, 1982. 256 с.

  16. Харрис П. Углеродные нанотрубы и родственные структуры. Новые материалы ХХI в. М.: Техносфера, 2003. 336 с.

  17. Zhukov A.V., Bouffanais R., Fedorov E.G., Belonenko M.B. // J. Appl. Phys. 2013. V. 114. Art. No. 143106.

  18. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука, 1987. 601 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал