Известия РАН. Серия физическая, 2022, T. 86, № 9, стр. 1292-1296

ВВЕДЕНИЕ

Современные направления развития спинтроники включают в себя эффекты, связанные с управлением и воздействием на спиновые токи в различных структурах [1, 2], таких как скирмионы [3, 4], многослойные спин-туннельные элементы [5, 6] и т.д. В частности, в работе [7] изучалось влияние внешнего магнитного поля на зависимости сопротивления элемента анизотропного магниторезистивного (АМР) датчика со структурой “barber-pole” в приближении, когда распределение тока можно считать однородным. В данной работе изучаются особенности прохождения электрического тока в таких датчиках, элементами которых являются пластины косоугольной формы толщиной порядка 10 нм. Решение задачи электростатики о распределении электрического потенциала U в таком случае соответствует решению уравнения Лапласа ∆U = 0, основываясь на котором можно рассчитать распределение плотности тока. Для этого были использованы методы сопряженных функций и конформного преобразования координат, предложенные Максвеллом [8] и активно использующиеся для решения задач электромагнетизма [9, 10]. Однако данные методы в случае решения задач электростатики справедливы только для однородных изотропных проводящих сред, что для исследуемого образца в первом приближении выполняется, так как величина магниторезистивного эффекта не превышает 2%. Но точный расчет распределения плотности тока в среде с АМР эффектом приводит к более сложному дифференциальному уравнению Лапласа для электрического потенциала с переменными коэффициентами, анализ которого и результаты численного решения для указанной косоугольной пластины также отражены в данной работе.

ПРИМЕНЕНИЕ МЕТОДА СОПРЯЖЕННЫХ ФУНКЦИЙ

Суть метода сопряженных функций состоит в том, что скалярный потенциал U (x, y) заменяется комплексным потенциалом

где z = x + iy. Мнимая часть этого потенциала представляет собой функцию потока, линии равного уровня которой V (x, y) = const совпадают с силовыми линиями электрического поля. Идея метода конформных преобразований состоит в том, что уравнение Лапласа для комплексного потенциала в однородной изотропной двумерной среде рассматривается в той области, в которой его решение хорошо известно. После этого полученное решение конформно отображается на интересующую область, в данном случае в форме косоугольной пластины. Так как форма исследуемого проводника представляет собой многоугольник, для конформного отображения комплексной полуплоскости было использовано преобразование Шварца–Кристоффеля [11]: где β_n ≡ α_n/π, α_n – углы многоугольника в радианах, a_n – точки на вещественной оси верхней комплексной полуплоскости z₁, а C и C₁ – константы, которые определяются из условий соответствия границ.

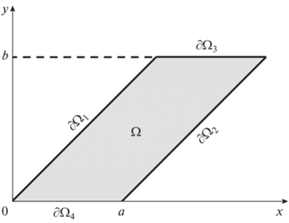
В общем случае рассмотрим четырехугольный проводник, ограниченный областью Ω. Граничное условие для потенциала U определяется тем, что к границам проводника ∂Ω₁ и ∂Ω₂ подведены идеальные контакты, то есть потенциал вдоль этих границ постоянный, и задается разность потенциалов между этими границами U₁ – U₂. Граничные условия также соответствуют отсутствию тока через боковые поверхности проводника ∂Ω₃ и ∂Ω₄. Поскольку линии равного уровня функции потока совпадают с силовыми линиями электрического поля, условие отсутствия тока через границу проводника можно записать в виде ${{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial{ \vec {n}}}}} \right. \kern-0em} {\partial{ \vec {n}}}} = 0,$ где $\vec {n}$ – внешняя нормаль к границе проводника. Пример такой области в виде косоугольной пластины представлен на рис. 1.

Окончательно задача имеет следующий вид:

К сожалению, конформные преобразования позволяющие легко осуществлять дальнейшие расчеты, удается построить лишь для ограниченного числа областей, в подавляющем же большинстве случаев преобразование записывается лишь в виде интеграла от функции комплексного переменного. Такая же ситуация наблюдается и при конформном отражении на внутреннюю область косоугольной пластины (рис. 1). Однако в настоящей работе удалось найти способ, позволяющий получить решение, выраженное в элементарных функциях. Это достигается за счет того, что рассматривается решение для полубесконечной косоугольной пластины, после чего результаты “сшиваются” в тех местах, где распределение плотности тока близко к равномерному. При этом оценивается возникающая погрешность, что позволяет достаточно легко определить параметры проводников, для которых применим предложенный метод.

Сначала найдем отображение верхней комплексной полуплоскости z₁ на прямоугольную полубесконечную полосу в плоскости z₀, решение задачи (4) в которой тривиально и соответствует однородному распределению плотности тока. В выбранной геометрии из условия соответствия границ следует, что постоянные C = 1 и C₁ = 0, а интеграл Шварца–Кристоффеля (3) имеет вид:

где

Для отображения решения задачи распределения потенциала в полубесконечной пластине в плоскости z₀ на верхнюю комплексную полуплоскость z₁ необходимо также найти обратное преобразование, которое нетрудно получить из (5) и (6):

Далее получим преобразование верхней комплексной полуплоскости z₁ на полубесконечную косоугольную пластину с острым углом α = 45° (рис. 1). Интеграл Шварца–Кристоффеля (3) в таком случае равен:

Определив константы C и C₁ из условия соответствия границ в выбранной геометрии и вычислив интеграл (8) в соответствии с [12], получим окончательное преобразование, отражающее полубесконечную полосу на полубесконечную косоугольную пластину с острым углом α = 45°:

Введем безразмерный параметр длины косоугольной пластины σ:

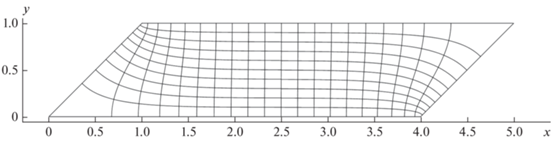
где a и b – размеры пластины, показанные на рис. 1. Согласно закону Ома, вектор плотности тока в однородном изотропном проводнике сонаправлен с вектором напряженности, поэтому силовые линии являются также и линиями тока в таком проводнике. Картина линий тока и эквипотенциалей, построенная по формулам (9) с учетом зеркального отражения и “сшивания” для проводника с размерами a = $\sqrt 2 $ и σ = 5, представлена на рис. 2. Отметим, что при σ > 5 величина относительной погрешности, отражающая несовпадение центральных эквипотенциалей, не превышает 0.2%.

Полученное решение имеет очень важное значение с точки зрения контроля точности, так как при численном решении аналогичной задачи в рассматриваемом элементе возникают сингулярности в области тупых углов (рис. 1). Наличие точного аналитического решения позволяет выполнить правильную регуляризацию таких особых областей и получить корректное численное решение задачи.

УЧЕТ АНИЗОТРОПНЫХ СВОЙСТВ АМР ЭЛЕМЕНТА

Как уже было сказано, уравнение (2) справедливо только для однородных изотропных сред. В анизотропной среде направления векторов напряженности электрического поля $\vec {E}$ и плотности тока $\vec {j}$ в общем случае не совпадают и связаны друг с другом соотношением:

где ρ_ik – тензор удельного сопротивления. В работе [13] было показано, что величина АМР эффекта в отсутствии внешнего магнитного поля зависит только от взаимной ориентации векторов намагниченности $\vec {M}$ и плотности тока $\vec {j}$ в произвольной точке проводника. Связь векторов $\vec {E}$ и $\vec {j}$ может быть задана следующим образом: где $\vec {m}$ – единичный вектор, совпадающий по направлению с вектором намагниченности $\vec {M}$ в среде; ρ_⟘ и ρ_∥ – удельные сопротивления при протекании тока в направлениях, перпендикулярном вектору $\vec {m}$ и параллельном ему соответственно; ρ_H – удельное холловское сопротивление. Последнее слагаемое в уравнении (4) определяет аномальное холловское электрическое поле [14]. Ввиду того, что в данной работе рассматриваются тонкие пленки, в которых векторы намагниченности и плотности тока лежат в плоскости пленки, аномальное холловское электрическое поле направленно перпендикулярно поверхности проводника и не влияет на распределение потенциала в его плоскости.

Введем систему координат в соответствии с рис. 1. Тогда, выразив плотность тока из (12) и подставив в уравнение ${\text{div}}{\kern 1pt} \vec {j} = 0,$ можно получить обобщенное уравнение Лапласа для потенциала U электрического поля внутри магниторезистивного элемента при наличии в данном элементе неоднородного стационарного распределения плотности электрического тока:

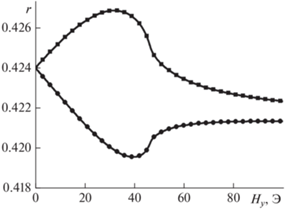
где ${{\beta }} = {{\Delta {{\rho }}} \mathord{\left/ {\vphantom {{\Delta {{\rho }}} {{{{{\rho }}}_{\parallel }}}}} \right. \kern-0em} {{{{{\rho }}}_{\parallel }}}} = {{{{{{\rho }}}_{\parallel }} - {{{{\rho }}}_{ \bot }}} \mathord{\left/ {\vphantom {{{{{{\rho }}}_{\parallel }} - {{{{\rho }}}_{ \bot }}} {{{{{\rho }}}_{\parallel }}}}} \right. \kern-0em} {{{{{\rho }}}_{\parallel }}}}.$ Было выполнено численное решение уравнения (13) для косоугольной пластины, изображенной на рис. 1, с граничными условиями, аналогичными (4). Распределение вектора $\vec {m}\left( {x,y} \right)$ определялось в рамках теории, описанной в [15]. Расчет проводился для параметров a = 7 мкм, b = 10 мкм и β = 0.02, что соответствует образцу, рассматриваемому в работе [7]. На основе полученных результатов были также рассчитаны зависимости безразмерного сопротивления r от величины внешнего магнитного поля ${{H}_{y}},$ направленного вдоль и против оси $y$ на рис. 1. Безразмерное сопротивление определяется следующим выражением: где R – полное сопротивление пластины, δ – толщина пластины.

Рассчитанные зависимости показаны на рис. 3. На рис. 3 можно видеть, что линейные участки кривых при малом магнитном поле до 15 Э идут практически под одним углом, однако затем кривые выходят на максимальное и минимальное значения. С увеличением магнитного поля свыше 80 Э полоска практически полностью перемагничивается в вертикальном направлении, поэтому сопротивление в обоих случаях стремится к некоторому новому значению, которое отличается от первоначального. Следует особо отметить, что кривые не симметричны. Данный эффект является следствием неоднородности распределения тока в среде с анизотропией сопротивления и не может быть получен в случае пренебрежения влиянием АМР эффекта на распределение тока.

Учет этого эффекта позволяет также получить теоретические вольт-эрстедные характеристики для АМР датчика, которые отличаются от представленных в работе [7]. Если в случае упрощённой модели однородного протекания тока положения максимумов теоретической и экспериментальной не совпадали и требовалось сжатие теоретической кривой вдоль оси абсцисс, то в данном случае максимумы совпадают в точности.

ЗАКЛЮЧЕНИЕ

Таким образом, было решено двумерное уравнение Лапласа для электрического потенциала в области косоугольного магниторезистивного элемента (рис. 2). представленное аналитическое решение, полученное в рамках метода сопряженных функций и конформных преобразований, позволяет контролировать точность численного решения аналогичной задачи с целью правильной регуляризации решения в особых областях. В описанной задаче такие особые области находятся в тупых углах на рис. 1, вблизи которых плотность тока стремится к бесконечности.

Учет АМР эффекта приводит к более сложному обобщенному уравнению Лапласа, решение которого в рамках метода сопряженных функций не представляется возможным. Численное решение уравнения позволило обнаружить асимметрию в графиках зависимостей сопротивления элемента от внешнего магнитного поля (рис. 3). Помимо обнаружения данного эффекта, учет АМР свойств позволил также получить более точные графики выходных характеристик датчика магнитного поля со структурой “barber-pole”, которые лучше согласуются с экспериментом по сравнению с упрощенной моделью однородного протекания тока в образце в работе [7].

Работа поддержана Фондом развития теоретической физики и математики “БАЗИС”.