Известия РАН. Серия физическая, 2023, T. 87, № 1, стр. 30-33
Взаимодействие уединенных электромагнитных волн в двумерной графеновой сверхрешетке
О. Ю. Бабина 1, С. Ю. Глазов 1, 2, *, И. Н. Федулов 3
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Волгоградский государственный социально-педагогический университет”
Волгоград, Россия
2 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Волгоградский государственный медицинский университет” Министерства здравоохранения
Российской Федерации
Волгоград, Россия
3 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Югорский государственный университет”
Ханты-Мансийск, Россия
* E-mail: ser-glazov@yandex.ru
Поступила в редакцию 29.08.2022
После доработки 16.09.2022
Принята к публикации 26.09.2022
- EDN: JHFRGW
- DOI: 10.31857/S0367676522700053
Аннотация
Изучено взаимное влияние солитонов, распространяющихся вдоль осей двумерной сверхрешетки на основе графена по взаимоперпендикулярным направлениям. Показано, что вследствие неаддитивности энергетического спектра структуры область перекрытия солитонов претерпевает характерные изменения, связанные с образованием импульсов, распространяющихся вдоль фронтов взаимодействующих уединенных волн.
ВВЕДЕНИЕ
Изучение оптических свойств графеновых структур – важное и актуальное направление современных исследований физики графена. Несмотря на пока еще существующие сложности технологического плана в получении графеновых сверхструктур, активно ведутся теоретические и экспериментальные исследования одномерных [1, 2] и двумерных (2D) [3–9] сверхрешеток на основе графена (ГСР). На сегодняшний день в данной области получено множество интересных результатов. В ГСР возможна генерация и усиление электромагнитных волн, в частности уединенных электромагнитных импульсов [10–15], что уже в недалеком будущем несомненно будет иметь важное практическое значение [16, 17]. Одномерная ГСР представляет собой слой графена на полосчатой подложке из чередующихся полос, например, оксида и карбида кремния (SiO2 и SiC) соответственно. Подложка из SiO2 не влияет на энергетический спектр графена, а в результате взаимодействия графена с подложкой из SiC появляется запрещенная зона (“щель”) шириной 0.26 эВ. Чередование щелевой и бесщелевой модификации графена приводит к образованию минизонного спектра. Ось сверхрешетки в этом случае направленно перпендикулярно чередующимся полосам SiO2 и SiC. Если же вместо полосчатой взять подложку, образуемую периодически чередующимися в шахматном порядке прямоугольными областями оксида и карбида кремния, то получится 2D ГСР. Модельный энергетический спектр такой сверхрешетки предложен в работе [3], а в работах [5, 6] исследовалось распространение электромагнитных импульсов в 2D ГСР. В данной работе численно исследовано взаимодействие уединенных электромагнитных импульсов (УЭИ), распространяющихся вдоль осей 2D ГСР по взаимоперпендикулярным направлениям.
ОСНОВНЫЕ УРАВНЕНИЯ
Спектр 2D ГСР, состоящей из чередующихся в шахматном порядке прямоугольных областей щелевого и бесщелевого графена, в одноминизонном приближении имеет вид [3]
(1)
$\begin{gathered} \varepsilon (\vec {p}) = \\ = \,\, \pm \sqrt {\Delta _{0}^{2} + \Delta _{1}^{2}\left( {1 - \cos ({{p}_{x}}{{d}_{1}})} \right) + \Delta _{2}^{2}\left( {1 - \cos ({{p}_{у}}{{d}_{2}})} \right)} , \\ \end{gathered} $Эволюция УЭИ описывается уравнением д’Аламбера для векторного потенциала с учетом столкновений
(2)
$\begin{gathered} \frac{{{{\partial }^{2}}{{\vec {A}}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{\vec {A}}}}}{{\partial {{y}^{2}}}} - \frac{{\text{1}}}{{{{{\text{V}}}^{{\text{2}}}}}}\frac{{{{\partial }^{2}}{{\vec {A}}}}}{{\partial {{t}^{2}}}} + \\ + \,\,\frac{{4\pi }}{c}{{{\vec {j}}}_{0}}({{{\text{A}}}_{x}}{\text{,}}{{{\text{A}}}_{y}}) = - \frac{{4\pi }}{c}{{{\vec {j}}}_{{st}}}({{{\text{A}}}_{x}}{\text{,}}{{{\text{A}}}_{y}}), \\ \end{gathered} $Плотность электрического тока определяется в виде
(3)
$\vec {j} = - e\sum {n(\vec {p})\vec {\upsilon }\left( {\vec {p} + \frac{e}{c}{{\vec {A}}}(\vec {r},t)} \right)} ,$(4)
$\frac{{\partial п{\text{(}}\vec {p}{\text{)}}}}{{\partial t}} - \frac{e}{с}\frac{{\partial {{\vec {A}}}}}{{\partial t}}\frac{{\partial n{\text{(}}\vec {p}{\text{)}}}}{{\partial{ \vec {p}}}} = - \nu \left( {n\left( {\vec {p}} \right) - {{n}_{0}}\left( {\vec {p}} \right)} \right).$Разлагая скорость электронов в двумерный ряд Фурье и предполагая электронный газ невырожденным, имеем выражение для плотности тока
(5)
$\begin{gathered} {{{\vec {j}}}_{0}} = - \frac{{e{{n}_{0}}}}{a}\left( {\sum\limits_{n = 1}^\infty {\sum\limits_{m = - \infty }^\infty {{{В}_{{nm}}}\sin (n{{\varphi }_{x}})\cos (m{{\varphi }_{y}})} } } \right., \\ \left. {\sum\limits_{n = 1}^\infty {\sum\limits_{m = - \infty }^\infty {{{C}_{{nm}}}\sin (n{{\varphi }_{y}})\cos (m{{\varphi }_{x}})} } } \right), \\ \end{gathered} $${{a}_{{nm}}}\, = \,\frac{{\Delta _{1}^{2}{{d}_{1}}}}{{2{{\pi }^{2}}}}\int\limits_{ - \pi }^\pi {\int\limits_{ - \pi }^\pi {\frac{{\sin (x)\sin (nx)\cos (my)dxdy}}{{\sqrt {\Delta _{0}^{2}\, + \,\Delta _{1}^{2}\left( {1 - \cos (x)} \right)\, + \,\Delta _{2}^{2}\left( {1 - \cos (y)} \right)} }}} } .$ Cnm вычисляется аналогично Bnm посредством разложения в ряд Фурье проекции скорости электронов на ось y.
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
Решение уравнения (2) производится численно с использованием схемы типа “крест”. Периоды сверхрешетки выбираются равными d1= d2= = d = 2 ⋅ 10–6 см, при таком выборе параметры энергетического спектра (1) составляют Δ0 = = 0.4217Δ (для SiC Δ = 0.13 эВ), Δ1 = Δ2 = 0.3318Δ. Степень неаддитивности спектра будет определяться количеством перекрестных членов в его разложении в ряд Фурье.
(6)
$\begin{gathered} \varepsilon (\vec {p}) = \Delta \left\{ {{{g}_{1}} - \frac{{{{g}_{2}}}}{2}\left[ {\cos \left( {{{p}_{x}}d} \right) + \cos \left( {{{p}_{у}}d} \right)} \right] - } \right. \\ \left. { - _{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}^{{}}{{g}_{3}}\cos \left( {{{p}_{x}}d} \right)\cos \left( {{{p}_{у}}d} \right)} \right\}. \\ \end{gathered} $(7)
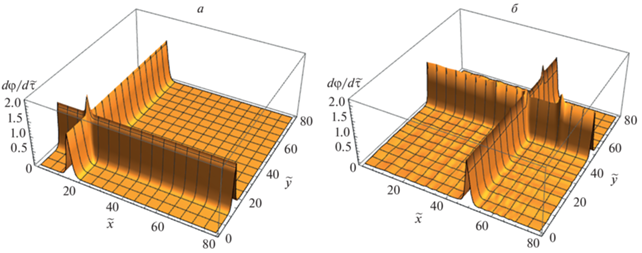
$\begin{gathered} \frac{{{{\partial }^{2}}{{\varphi }_{x}}}}{{\partial {{{\tilde {t}}}^{2}}}} - \frac{{{{\partial }^{2}}{{\varphi }_{x}}}}{{\partial {{{\tilde {x}}}^{2}}}} - \frac{{{{\partial }^{2}}{{\varphi }_{x}}}}{{\partial {{{\tilde {y}}}^{2}}}} + \sin {{\varphi }_{x}}(1 + \beta \cos {{\varphi }_{y}}) = 0, \\ \frac{{{{\partial }^{2}}{{\varphi }_{y}}}}{{\partial {{{\tilde {t}}}^{2}}}} - \frac{{{{\partial }^{2}}{{\varphi }_{y}}}}{{\partial {{{\tilde {x}}}^{2}}}} - \frac{{{{\partial }^{2}}{{\varphi }_{y}}}}{{\partial {{{\tilde {y}}}^{2}}}} + \sin {{\varphi }_{y}}(1 + \beta \cos {{\varphi }_{x}}) = 0, \\ \end{gathered} $Большой интерес представляет исследование взаимодействия нелинейных уединенных импульсов. В отсутствие неаддитивности спектра, когда параметр β = 0, солитоны, распространяющиеся вдоль взаимно перпендикулярных направлений, не взаимодействуют, вследствие чего их форма сохраняется. Однако в случае слабой неаддитивности результаты численного расчета показывают взаимное влияние распространяющихся уединенных волн даже в случае малых потенциалов.
Непосредственно результаты численного моделирования столкновений солитонов в 2D ГСР показаны на рис. 1. По горизонтальным осям отложены безразмерные координаты, по вертикальной – модуль напряженности электрического поля, также выраженный в безразмерных единицах. На рис. 1б хорошо виден результат взаимного влияния солитонов друг на друга. В области перекрытия солитонов наблюдается уменьшение амплитуды с одновременным образованием двух импульсов, со значительной скоростью распространяющихся вдоль фронтов уединенных волн.
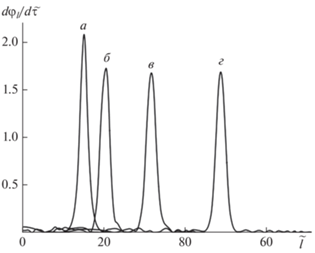
Для анализа картины эволюции УЭИ удобно выбрать направление под углом 45° к осям ГСР и наблюдать за изменением потенциала и напряженности электрического поля вдоль этого направления. Результаты моделирования изменения формы УЭИ представлены на рис. 2. Хорошо заметно быстрое уменьшение амплитуды на начальном этапе распространения, а также то, что по достижении амплитудой определенного значения в дальнейшем она перестает изменяться. В процессе распространения изменяется также и форма импульса. В целом картина эволюции формы УЭИ выглядит как подстраивание импульса под среду, в которой происходит его распространение.
Рис. 2.
Профиль импульса (срез под углом 45° к осям ГСР) для $\tilde {t} = 0$ (a), 10 (б), 30 (в), 60 (г).
При учете столкновений электронов с решеткой амплитуды УЭИ быстро уменьшаются, поэтому основной задачей является увеличение времени его жизни. Для увеличения времени жизни солитонной системы необходимо осуществить подпитку энергии с помощью внешнего электрического поля или тока [5, 6].
ЗАКЛЮЧЕНИЕ
Численно исследовано распространение двух взаимодействующих нелинейных УЭИ в 2D ГСР в бесстолкновительном приближении и с учетом столкновений. Получена картина взаимного влияния и эволюции солитонов, распространяющихся вдоль осей сверхрешетки во взаимно перпендикулярных направлениях. В бесстолкновительном режиме после переходного процесса наблюдается состояние с установившейся амплитудой в области перекрытия солитонов и образование импульсов, бегущих вдоль фронтов уединенных волн. Такая эволюция рассматриваемой пары солитонов вызвана неаддитивностью энергетического спектра, приводящей к взаимосвязи ортогональных составляющих векторного потенциала. Разработан программный комплекс для численного моделирования распространения уединенных электромагнитных волн в 2D ГСР.
Список литературы
Ratnikov P.V. // JETP Lett. 2009. V. 90. No. 6. P. 469.
Ratnikov P.V. // Phys. Rev. B. 2020. V. 101. Art. No. 125301.
Kryuchkov S.V., Popov C.A. // J. Nano-Electron. Phys. 2017. V. 9. No. 2. Art. No. 02013.
Бадикова П.В., Глазов С.Ю., Сыродоев Г.А. // ФТП. 2019. Т. 53. № 7. С. 927; Badikova P.V., Glazov S.Yu., Syrodoev G.A. // Semiconductors. 2019. V. 53. No. 7. P. 911.
Глазов С.Ю., Сыродоев Г.А. // Изв. РАН. Сер. физ. 2020. Т. 84. № 1. С. 128; Glazov S.Yu., Syrodoev G.A. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. No. 1. P. 98.
Glazov S.Yu., Syrodoev G.A. // J. Phys. Conf. Ser. 2021. V. 1740. No. 1. Art. No. 012062.
Бадикова П.В., Глазов С.Ю., Сыродоев Г.А. // Изв. РАН. Сер. физ. 2020. Т. 84. № 1. С. 38; Badikova P.V., Glazov S.Yu., Syrodoev G.A. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. No. 1. P. 30.
Forsythe C., Zhou X., Watanabe K. et al. // Nature Nanotech. 2018. V. 13. P. 566.
Zhang Y., Kim Y., Gilbert M.J. et al. // NPJ 2D Mater. Appl. 2018. V. 2. P. 31.
Popa D., Sun Z., Torrisi F. et al. // Appl. Phys. Lett. 2010. V. 97. Art. No. 203106.
Martin-Vergara F., Rus F., Villatoro F.R. // Nonlinear Syst. 2018. V. 2. P. 85.
Kryuchkov S.V., Kukhar’ E.I. // Physica B. 2013. V. 408. P. 188.
Smirnova D.A., Shadrivov I.V., Smirnov A.I. et al. // Laser Photon. Rev. 2014. V. 8. P. 291.
Bludov Yu.V., Smirnova D.A., Kivshar Yu.S. et al. // Phys. Rev. B. 2015. V. 91. Art. No. 045424.
Кухарь Е.И., Крючков С.В., Ионкина Е.С. // ФТП. 2018. Т. 52. № 6. С. 620; Kukhar E.I., Kryuchkov S.V., Ionkina E.S. // Semiconductors. 2018. V. 52. No. 6. P. 766.
Крючков С.В., Капля Е.В. // ЖТФ. 2003. Т. 48. № 5. P. 53; Kryuchkov S.V., Kaplya E.V. // Tech. Phys. 2003. V. 48. No. 5. P. 576.
Sun Z., Hasan T., Ferrari A.C. // Physica E. 2012. V. 44. P. 1082.
Эпштейн Э.М. // ФТТ. 1977. Т. 19. № 11. С. 3456; Epshtein E.M. // Sov. Phys. Solid State. 1977. V. 19. No. 11. P. 2020.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая