Известия РАН. Серия физическая, 2023, T. 87, № 1, стр. 56-60

Умножение частоты в сильноточном релятивистском гиротроне для получения мощного излучения терагерцевого диапазона

А. Н. Леонтьев^1, *, Р. М. Розенталь^1, 2, Н. С. Гинзбург¹, И. В. Зотова¹, А. М. Малкин^1, 2, А. С. Сергеев¹

¹ Федеральное государственное бюджетное учреждение науки “Федеральный исследовательский центр Институт прикладной физики Российской академии наук”
Нижний Новгород, Россия

² Федеральное государственное автономное образовательное учреждение высшего образования “Национальный исследовательский Нижегородский государственный университет имени Н.И. Лобачевского”
Нижний Новгород, Россия

^* E-mail: leontiev@ipfran.ru

Поступила в редакцию 29.08.2022
После доработки 16.09.2022
Принята к публикации 26.09.2022

EDN: JJCLJD
DOI: 10.31857/S0367676522700107

Полный текст (PDF)

Аннотация

В рамках усредненных уравнений и на основе трехмерного моделирования методом крупных частиц исследован режим умножения частоты в сильноточном релятивистском гиротроне диапазона 0.1 ТГц. Показано, что отношение мощности излучения на третьей гармонике к уровню генерации на основном циклотронном резонансе может составлять 0.4–0.8%, что позволяет рассчитывать на получение излучения в диапазоне 0.3 ТГц субмегаваттного уровня мощности.

ВВЕДЕНИЕ

В настоящее время одними из наиболее мощных источников излучения терагерцевого диапазона являются гиротроны, которые в импульсном режиме обеспечивают уровни мощности в сотни киловатт в терагерцевом диапазоне при работе на основном циклотронном резонансе [1, 2]. Однако необходимость создания достаточно сильных магнитных полей в большом объеме является одним из ключевых факторов, ограничивающих продвижение мощных гиротронов в более высокочастотные диапазоны. К примеру, в случае сильноточного гиротрона диапазона 0.3 ТГц требуется магнитное поле около 20 Тл [3].

В этой связи, как с целью повышения частоты генерации при заданной величине магнитного поля, так и для снижения магнитного поля на заданной частоте, представляет интерес исследование возбуждения в гиротронах на циклотронных гармониках. Одной из привлекательных возможностей здесь является использовании эффекта умножения частоты [4, 5]. При этом, поскольку электронный пучок является нелинейной средой, в нем под воздействием внешней или сгенерированной самим пучком низкочастотной волны возникают гармоники тока, которые обеспечивают последующее высокочастотное излучение на гармониках частоты низкочастотной волны.

В случае слаборелятивистских винтовых электронных пучков значительным недостатком описанного механизма является низкий коэффициент нелинейной трансформации, который определяется как отношение мощности высокочастотного излучения к уровню низкочастотной генерации на основном циклотронном резонансе. Это обусловлено, с одной стороны, неэквидистантностью спектра мод цилиндрических волноводов, типично используемых в гиротронах, а, с другой, – быстрым спаданием коэффициентов связи с увеличением номера гармоники. В частности, проведенные в [6, 7] измерения мощности для слаборелятивистского гиротрона с рабочей частотой 0.26 ТГц показали, что значения коэффициента нелинейной трансформации на второй циклотронной гармонике на частоте 0.52 ТГц составили 10^–4 (т.е., около 0.01% относительно мощности излучения на первой гармонике), а для третьей циклотронной гармоники на частоте 0.78 ТГц – около 10^–6 (0.0001%). В то же время, хорошо известно, что степень спадания коэффициентов связи на гармониках уменьшается с увеличением энергии электронов [8].

В данной работе показано, что при использовании релятивистского сильноточного винтового электронного пучка, коэффициент нелинейной трансформации в гиротроне увеличивается на несколько порядков. В результате мощность генерации на третьей гармонике может составлять десятые доли процента относительно мощности генерации на первой гармонике.

МОДЕЛИРОВАНИЕ В РАМКАХ УСРЕДНЕННОГО ПОДХОДА

Рассмотрим модель гиротрона в виде отрезка слабонерегулярного цилиндрического волновода радиусом R₀, в котором винтовой электронный пучок возбуждает несколько ТЕ-мод с номерами n = 1, 2, 3… и значениями азимутального и радиального индексов m_n и q_n, соответственно. Будем полагать, что каждая мода взаимодействует с пучком на s_n-ой циклотронной гармонике; при этом частота излучения на заданной моде близка как к критической частоте моды в резонаторе $\bar {\omega }_{n}^{c},$ так и к величине ${{s}_{n}}\omega _{H}^{0},$ где $\omega _{H}^{0} = {{{{e{{H}_{0}}} \mathord{\left/ {\vphantom {{e{{H}_{0}}} {{{m}_{e}}c\gamma }}} \right. \kern-0em} {{{m}_{e}}c\gamma }}}_{0}}$ – гирочастота, H₀ – величина ведущего магнитного поля, γ₀ – релятивистский масс-фактор. Электрическое поле каждой из мод в рабочем пространстве может быть представлено в виде

(1)

${{\vec {E}}_{n}} = \operatorname{Re} \left( {{{A}_{n}}\left( {z,t} \right)\vec {E}_{ \bot }^{n}\left( r \right)\exp \left( {i{{s}_{n}}\omega _{H}^{0}t - i{{m}_{n}}\varphi } \right)} \right),$

где ${{A}_{n}}\left( {z,t} \right)$ – медленно меняющаяся комплексная амплитуда моды с номером n, функция $\vec {E}_{ \bot }^{n}\left( r \right)$ описывает радиальную структуру моды, φ – азимутальный угол. Электронно-волновое взаимодействие с учетом разброса по скоростям в электронном пучке может быть описано следующей системой уравнений (ср. с [9]):

(2)

$\begin{gathered} i\frac{{{{\partial }^{2}}{{a}_{n}}}}{{\partial {{Z}^{2}}}} + {{s}_{n}}\frac{{\partial {{a}_{n}}}}{{\partial \tau }} + \left( {i{{\Delta }_{n}} + i{{\delta }_{n}}\left( Z \right) + {{\sigma }_{n}}} \right){{a}_{n}} = \\ = i\frac{{{{G}_{n}}}}{{4{{\pi }^{2}}}}\frac{{\int\limits_0^{2\pi } {{{e}^{{i\left( {{{m}_{n}} - {{s}_{n}}} \right)\varphi }}}\int\limits_0^{2\pi } {\alpha \left( {{{p}_{0}}} \right)\int\limits_0^{2\pi } {{{p}^{s}}d{{\theta }_{0}}} d{{p}_{0}}d\varphi } } }}{{\int\limits_0^{2\pi } {\alpha \left( {{{p}_{0}}} \right)\sqrt {\bar {g}_{0}^{2} + 1 - \bar {g}_{0}^{2}{{{\left| {{{p}_{0}}} \right|}}^{2}}} d{{p}_{0}}} }}, \\ \sqrt {\bar {g}_{0}^{2} + 1 - \bar {g}_{0}^{2}{{{\left| {{{p}_{0}}} \right|}}^{2}}} \frac{{\partial p}}{{\partial Z}} + \frac{{\bar {g}_{0}^{2}}}{4}\frac{{\partial p}}{{\partial \tau }} + ip\left( {{{{\left| p \right|}}^{2}} - {{{\left| {{{p}_{0}}} \right|}}^{2}}} \right) = \\ = i\sum\limits_n {{{a}_{n}}{{{\left( {p{\text{*}}} \right)}}^{{{{s}_{n}} - 1}}}{{e}^{{ - i\left( {{{m}_{n}} - {{s}_{n}}} \right)\varphi }}}} , \\ \end{gathered} $

где

(3)

${{a}_{n}} = \frac{{e{{A}_{n}}{{J}_{{{{m}_{n}} - {{s}_{n}}}}}\left( {{{\nu }_{{{{m}_{n}},{{q}_{n}}}}}{{{{R}_{b}}} \mathord{\left/ {\vphantom {{{{R}_{b}}} {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}}} \right)}}{{mc\omega _{H}^{0}}}\frac{{s_{n}^{{{{s}_{n}}}}}}{{{{2}^{{{{s}_{n}} - 1}}}{{s}_{n}}!}}\frac{{\bar {\beta }_{{ \bot 0}}^{{{{s}_{n}} - 4}}}}{{{{\gamma }_{0}}}},$

безразмерная амплитуда поля

(4)

$Z = \frac{{\bar {\beta }_{{ \bot 0}}^{2}}}{{2{{{\bar {\beta }}}_{{||0}}}}}\frac{{\omega _{H}^{0}}}{c}z,\,\,\,\,\tau = \frac{{\bar {\beta }_{{ \bot 0}}^{4}}}{{8\bar {\beta }_{{||0}}^{2}}}\omega _{H}^{0}t,$

безразмерные продольная координата и время, ${{\bar {\beta }}_{{ \bot 0}}} = {{{{{\bar {V}}}_{{ \bot 0}}}} \mathord{\left/ {\vphantom {{{{{\bar {V}}}_{{ \bot 0}}}} с}} \right. \kern-0em} с}$ и ${{\bar {\beta }}_{{||0}}} = {{{{{\bar {V}}}_{{||0}}}} \mathord{\left/ {\vphantom {{{{{\bar {V}}}_{{||0}}}} с}} \right. \kern-0em} с}$ – средние значения нормированной поперечной и продольной скорости электронов на входе в область взаимодействия, ${{g}_{0}} = {{{{{\bar {\beta }}}_{{ \bot 0}}}} \mathord{\left/ {\vphantom {{{{{\bar {\beta }}}_{{ \bot 0}}}} {{{{\bar {\beta }}}_{{||0}}}}}} \right. \kern-0em} {{{{\bar {\beta }}}_{{||0}}}}}$ – соответствующий питч-фактор,

(5)

$p = \frac{{\left( {{{p}^{x}} + i{{p}^{y}}} \right){{e}^{{ - i{{s}_{n}}{{\omega }_{H}}t + i\left( {{{m}_{n}} - 1} \right)\varphi }}}}}{{m{{{\bar {V}}}_{{ \bot 0}}}{{\gamma }_{0}}}}$

нормированный на среднее начальное значение комплексный поперечный импульс,

(6)

${{\Delta }_{n}} = \frac{{8\bar {\beta }_{{||0}}^{2}s_{n}^{2}}}{{\bar {\beta }_{{ \bot 0}}^{4}}}\frac{{{{s}_{n}}\omega _{H}^{0} - \bar {\omega }_{n}^{c}}}{{\bar {\omega }_{n}^{c}}}$

циклотронная расстройка для моды с номером n,

(7)

${{\delta }_{n}}\left( Z \right) = \frac{{8\bar {\beta }_{{||0}}^{2}s_{n}^{2}}}{{\bar {\beta }_{{ \bot 0}}^{4}}}\frac{{\bar {\omega }_{n}^{c} - \omega _{n}^{c}\left( Z \right)}}{{\bar {\omega }_{n}^{c}}}$

геометрическая расстройка, описывающая профиль резонатора R(z), $\omega _{n}^{c}\left( Z \right) = {{{{\nu }_{{{{m}_{n}},{{q}_{n}}}}}c} \mathord{\left/ {\vphantom {{{{\nu }_{{{{m}_{n}},{{q}_{n}}}}}c} {R\left( z \right)}}} \right. \kern-0em} {R\left( z \right)}}$ – функция, задающая зависимость критической частоты моды с номером n от продольной координаты,

(8)

$\begin{gathered} {{G}_{n}} = 64\frac{{e{{I}_{b}}}}{{{{m}_{e}}{{c}^{3}}}}\frac{{{{{\bar {\beta }}}_{{||0}}}\bar {\beta }_{{ \bot 0}}^{{2\left( {{{s}_{n}} - 4} \right)}}}}{{{{\gamma }_{0}}}} \times \\ \times \,\,s_{n}^{3}\;{{\left( {\frac{{s_{n}^{{{{s}_{n}}}}}}{{{{2}^{{{{s}_{n}}}}}{{s}_{n}}!}}} \right)}^{2}}\frac{{J_{{{{m}_{n}} - {{s}_{n}}}}^{2}\left( {{{\nu }_{{{{m}_{n}},{{q}_{n}}}}}{{{{R}_{b}}} \mathord{\left/ {\vphantom {{{{R}_{b}}} {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}}} \right)}}{{\left( {\nu _{n}^{2} - m_{n}^{2}} \right)J_{{{{m}_{n}}}}^{2}\left( {{{\nu }_{{{{m}_{n}},{{q}_{n}}}}}} \right)}} \\ \end{gathered} $

– параметр возбуждения для пучка с радиусом инжекции R_b и током I_b, ${{\nu }_{{{{m}_{n}},{{q}_{n}}}}}$ – корень с номером q_n уравнения $J_{{{{m}_{n}}}}^{'}\left( \nu \right) = 0,$

(9)

${{\sigma }_{n}} = 4\frac{{\bar {\beta }_{{||0}}^{2}}}{{\bar {\beta }_{{ \bot 0}}^{4}}}\frac{{s_{n}^{2}}}{{{{Q}_{n}}}}$

коэффициент поглощения,

(10)

${{Q}_{n}} = \frac{{{{R}_{0}}}}{{{{d}_{n}}}}\left( {1 - \frac{{m_{n}^{2}}}{{\nu _{{{{m}_{n}},{{q}_{n}}}}^{2}}}} \right),$

омическая добротность для моды с номером n, d_n – соответствующая толщина скин-слоя. Для учета начального разброса электронов по поперечным скоростям использовалась гауссова функция распределения:

(11)

$\alpha \left( p \right) = \frac{{\sum\limits_{j = - M}^M {{{e}^{{ - {{j}^{2}}\chi }}}\int\limits_0^{2\pi } {p_{j}^{{{{s}_{n}}}}d{{\theta }_{0}}} } }}{{\sum\limits_{j = - M}^M {{{e}^{{ - {{j}^{2}}\chi }}}\sqrt {{{g}^{2}} + 1 - {{g}^{2}}{{{\left| {p_{j}^{0}} \right|}}^{2}}} } }},$

где целое число M определяет число фракций электронов, равное 2M + 1, p_j – значение комплексного поперечного импульса для j-й фракции электронов, χ – параметр относительной ширины гауссовой кривой распределения.

Будем считать, что на входе в пространство взаимодействия электроны равномерно распределены по фазам циклотронного вращения

(12)

${{p}_{j}}\left( {{\rm Z} = 0} \right) = p_{j}^{0}{{e}^{{i{{\theta }_{0}}}}},\,\,\,\,{{\theta }_{0}} \in [0,2\pi ).$

В свою очередь $p_{j}^{0} = \left( {1 + \varepsilon j} \right){{e}^{{i\theta }}},$ где ε – параметр абсолютной величины разброса.

Во входном и выходном сечениях пространства взаимодействия используется излучательное граничное условие [10]:

(13)

$\begin{gathered} {{a}_{n}}\left( {Z = 0,\tau } \right) - \frac{{{{e}^{{ - i{{\left( {{{\Delta }_{n}} + {{\delta }_{n}}\left( 0 \right) + {{\sigma }_{n}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\Delta }_{n}} + {{\delta }_{n}}\left( 0 \right) + {{\sigma }_{n}}} \right)} {{{s}_{n}}}}} \right. \kern-0em} {{{s}_{n}}}}}}}}}{{\sqrt {i\pi {{s}_{n}}} }} \times \\ \times \,\,\int\limits_0^\tau {\frac{{{{e}^{{ - i\left( {\tau - \tau {\kern 1pt} '} \right)}}}}}{{\sqrt {\tau - \tau {\kern 1pt} '} }}\frac{{\partial {{a}_{n}}\left( {0,\tau {\kern 1pt} '} \right)}}{{\partial Z}}d\tau {\kern 1pt} '} = 0, \\ {{a}_{n}}\left( {Z = L,\tau } \right) + \frac{{{{e}^{{ - i{{\left( {{{\Delta }_{n}} + {{\delta }_{n}}\left( L \right) + {{\sigma }_{n}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\Delta }_{n}} + {{\delta }_{n}}\left( L \right) + {{\sigma }_{n}}} \right)} {{{s}_{n}}}}} \right. \kern-0em} {{{s}_{n}}}}}}}}}{{\sqrt {i\pi {{s}_{n}}} }} \times \\ \times \,\,\int\limits_0^\tau {\frac{{{{e}^{{ - i\left( {\tau - \tau {\kern 1pt} '} \right)}}}}}{{\sqrt {\tau - \tau {\kern 1pt} '} }}\frac{{\partial {{a}_{n}}\left( {L,\tau {\kern 1pt} '} \right)}}{{\partial Z}}d\tau {\kern 1pt} '} = 0, \\ \end{gathered} $

где L – нормированная длина резонатора.

В использованных нормировках мощность излучения каждой из мод в выходном сечении находится по формуле

(14)

${{P}_{n}}\,\,\left[ {{\text{кВт}}} \right] = 511.765I\left[ A \right]\frac{{{{\gamma }_{0}}\beta _{{ \bot 0}}^{2}}}{{{{G}_{n}}}}{{\left. {\operatorname{Im} \left( {{{a}_{n}}\frac{{\partial a_{n}^{*}}}{{\partial Z}}} \right)} \right|}_{{Z = L}}}.$

Рассмотрим релятивистский гиротрон диапазона 0.1 ТГц с рабочей модой ТЕ_–4.2, возбуждаемый винтовым электронным пучком с энергией 500 кэВ и током 2 кА. Для удобства будем полагать, что рабочая мода на основной гармонике гирочастоты имеет номер 1, соответственно s₁ = 1, m₁ = –4, q₁ = 2. Известно, что для эффективного умножения излучения в гармонику с номером s_n, необходимо, чтобы азимутальные индексы мод на первой и n-ой циклотронных гармониках удовлетворяли соотношению

(15)

${{m}_{n}} = {{s}_{n}}{{m}_{1}},$

и, одновременно, выполнялось условие кратности критических частот

(16)

$\bar {\omega }_{n}^{c} \approx {{s}_{n}}\bar {\omega }_{1}^{c},$

Последнее условие удобно переписать для значений собственных чисел мод:

(17)

${{\nu }_{{{{m}_{n}},{{q}_{n}}}}} \approx {{s}_{n}}{{\nu }_{{{{m}_{1}},{{q}_{1}}}}}.$

Рассмотрим умножение в гармонику с номером s₂ = 3 на частоте 0.3 ТГц. Согласно условию (15), азимутальный индекс высокочастотной моды будет равен m₂ = –12. В свою очередь, условие (17) будет лучше всего выполняться для моды ТЕ_–12.4, так что q₂ = 4. Для величины начального разброса электронов по поперечным скоростям 20% и среднего начального значения питч-фактора g₀ = = 1 значения параметров в выражениях (11), (12) примут значения ε = 0.04, χ = 0.33.

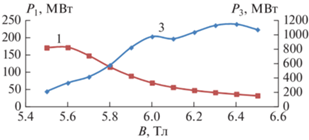
На рис. 1 показана рассчитанная на основе уравнений (2) зависимость мощности излучения от величины магнитного поля. Максимальная мощность излучения на основном циклотронном резонансе P₁ достигает почти 200 МВт при магнитном поле около 5.5 Tл и плавно спадает по мере его увеличения. В свою очередь, по мере роста магнитного поля, мощность излучения на третьей гармонике плавно нарастает, достигая максимального значения более 1 МВт.

Рис. 1.

Моделирование на основе усредненных уравнений. Зависимость мощности генерации на основной гармонике P₁ и третьей гармонике P₃ от величины магнитного поля.

ТРЕХМЕРНОЕ МОДЕЛИРОВАНИЕ МЕТОДОМ КРУПНЫХ ЧАСТИЦ

Для более полного анализа характеристик генерации на высоких циклотронных гармониках расчеты гиротрона были также выполнены на основе трехмерного PIC-моделирования методом крупных частиц с использованием программы CST Particle Studio. В моделировании винтовой электронный пучок с начальной энергией 500 кэВ, током 2 кА и разбросом по скоростям около 20% возбуждал резонатор гиротрона на моде ТЕ_-4.2 на частоте 0.1 ТГц. На рис. 2a представлена геометрия пространства взаимодействия, мгновенное положение макрочастиц и их распределение по энергиям. Использовалось около 300 тысяч макрочастиц, количество узлов сетки составляло около 25 млн. После окончания взаимодействия электронный пучок высаживался на стенку электродинамической системы в спадающем магнитном поле.

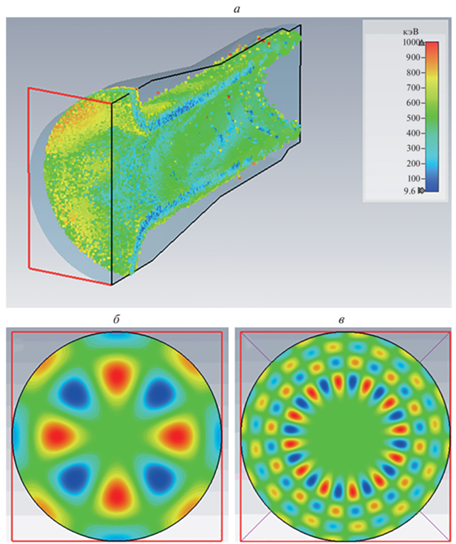
Рис. 2.

Геометрия пространства взаимодействия, мгновенное положение макрочастиц и их распределение по энергиям в трехмерном PIC моделировании (а), поперечное распределение возбуждаемого высокочастотного поля моды ТЕ_–4.2 на первой циклотронной гармонике (б) и моды ТЕ_–12.4 на третьей циклотронной гармонике (в).

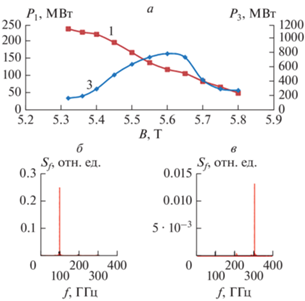
На рис. 2б и 2в показаны поперечные структуры высокочастотного поля для моды ТЕ_–4.2, возбуждаемой на первой гармонике гирочастота, и на моде ТЕ_–12.4, возбуждаемой на третьей гармонике. На рис. 3а показана зависимость мощности излучения от величины магнитного поля на основной рабочей моде ТЕ_–4.2 и моде ТЕ_–12.4. Частота излучения на третьей гармонике ровно в три раза превышает частоту генерации на первой гармонике и составляет 0.3 ТГц (рис. 3б и 3в). Максимальный уровень мощности на третьей гармонике достигает 0.8 МВт.

Рис. 3.

Результаты трехмерного PIC моделирования: Зависимость мощности генерации на основной гармонике P₁ и третьей гармонике P₃ от величины магнитного поля (а), спектр выходного излучения гиротрона на модах ТЕ_–4.2 (б) и ТЕ_–12.4 (в).

ЗАКЛЮЧЕНИЕ

Таким образом, результаты моделирования показывают возможность достижения в релятивистских гиротронах субмегаваттного уровня мощности излучения в диапазоне 0.3 ТГц в режиме умножения на третьей циклотронной гармонике с кратным снижением величины магнитного поля. Отметим, что в настоящее время ведется разработка релятивистских гиротронов с выходной мощностью около 80 МВт с рабочей частотой 0.3 ТГц на основном циклотронном резонансе [3]. Соответственно, в подобных гиротронах в режиме умножения частоты можно рассчитывать на получение излучения с уровнем мощности в сотни киловатт в диапазоне около 0.9 ТГц.

Работа выполнена в рамках государственного задания № 0030-2021-0027 (программа “Развитие техники, технологий и научных исследований в области использования атомной энергии в Российской Федерации на период до 2024 г.”).

Список литературы

Sabchevski S., Glyavin M., Mitsudo S. et al. // J. Infrared Millim. THz Waves. 2021. V. 42. No. 7. P. 715.
Thumm M. // J. Infrared Millim. THz Waves. 2020. V. 41. No. 1. P. 1.
Rozental R.M., Danilov Yu.Yu., Leontyev A.N. et al. // IEEE Trans. Electron Dev. 2022. V. 69. No. 3. P. 1451.
Завольский Н.А., Нусинович Г.С., Павельев А.Б. // Изв. вузов. Радиофиз. 1988. Т. 31. № 3. С. 361.
Idehara T., Ogawa I., Shimizu Y., Tatsukawa T. // J. Infrared Millim. THz Waves. 1998. V. 19. P. 803.
Golubiatnikov G.Yu., Koshelev M.A., Tsvetkov A.I. et al. // IEEE Trans. Terahertz Sci. Tech. 2020. V. 10. No. 5. P. 502.
Glyavin M., Zotova I., Rozental R. et al // J. Infrared Millim. THz Waves. 2020. V. 41. P. 1245.
Братман В.Л., Гинзбург Н.С., Нусинович Г.С. и др. // В кн.: Релятивистская высокочастотная электроника. Горький: ИПФАН СССР, 1979. С. 157.
Dumbrajs O., Saito T., Tatematsu Y., Yamaguchi Y. // Phys. Plasmas. 2016. V. 23. Art. No. 093109.
Ginzburg N.S., Nusinovich G.S., Zavolsky N.A. // Int. J. Electron. 1986. V. 61. No. 6. P. 881.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал