1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 87, № 3, 2023

Известия РАН. Серия физическая, 2023, T. 87, № 3, стр. 446-449

Эффекты старения в критическом поведении анизотропных ультратонких гейзенберговских пленок

М. А. Шляхтич 1, 2, *, П. В. Прудников 2

1 Федеральное государственное автономное образовательное учреждение высшего образования “Сибирский федеральный университет”
Красноярск, Россия

2 Федеральное государственное автономное образовательное учреждение высшего образования “Омский государственный университет имени Ф.М. Достоевского”
Омск, Россия

* E-mail: mshlyakhtich@sfu-kras.ru

Поступила в редакцию 28.09.2022
После доработки 27.10.2022
Принята к публикации 25.11.2022

Полный текст (PDF)

Аннотация

Представлены результаты исследования методом Монте-Карло неравновесных свойств ферромагнитных пленок Гейзенберга. Наблюдались эффекты старения при неравновесном критическом поведении. Расчеты проводились как из высокотемпературного, так и из низкотемпературного начального состояния. Получено характерное время корреляции, расходящееся при температуре перехода в термодинамическом пределе, как функция размера системы и времени ожидания.

ВВЕДЕНИЕ

Изучению различных свойств ультратонких пленок, в том числе и магнитных, посвящено большое количество экспериментальных работ [1–3]. Интерес к таким объектам очень высок из-за широкого спектра практического применения этих систем. Благодаря сильному влиянию формы и кристаллографической анизотропии подложки магнитное упорядочение в ультратонких ферромагнитных пленках очень сложно. В связи с этим теоретические расчеты спиновых моделей и разработка методов компьютерного моделирования имеют важное значение для рационализации и управления новыми экспериментами.

Большое количество явлений проявляются в статистических системах с медленной динамикой. К таким явлениям относятся: резкое замедление процессов релаксации, эффекты памяти, эффекты старения и т.д. Ввиду этого в последнее время системы с медленной динамикой вызывают большой теоретический и экспериментальный интерес [4–7]. После длительного времени система с медленной динамикой даже после малого возмущения не достигает равновесия. В связи с этим ее динамика не является инвариантной ни к переносу времени, ни к обращению времени, как это обычно происходит в тепловом равновесии. Эффекты старения проявляются во время этой бесконечной релаксации. Таким образом, двухвременные величины, такие как отклик и корреляционные функции, зависят от двух времен: времени ожидания tw и времени наблюдения t – tw (t > tw), и их затухание в зависимости от t происходит медленнее при больших tw. В отличие от одновременных величин (например, параметра порядка), сходящихся к асимптотическим значениям в пределе больших времен, двухвременные величины явно характеризуются признаками старения.

ОПИСАНИЕ МОДЕЛИ

Были исследованы тонкие ферромагнитные пленки, описываемые гамильтонианом Гейзенберга:

(1)
$H = - J\sum\limits_{\left\langle {i,j} \right\rangle }^{Ns} {\left[ {\left( {1 - \Delta (N)} \right)\left( {S_{i}^{x}S_{j}^{x} + S_{i}^{y}S_{j}^{y}} \right) + S_{i}^{z}S_{j}^{z}} \right]} ,$
где $\left( {S_{i}^{x};S_{i}^{y};S_{i}^{z}} \right)$ – единичный вектор в направлении классического магнитного момента в узле i решетки; J > 0 – константа ферромагнитного обменного взаимодействия; Δ(N) – константа анизотропии; Δ = 0 соответствует изотропному случаю Гейзенберга; Δ = 1 – случай Изинга. На систему накладывались периодические граничные условия в плоскости пленки и свободные граничные условия в перпендикулярном направлении.

Моделирование проводилось для систем размером ${{N}_{S}} = L \times L \times N,$ где N – число слоев в пленке, а L = 128 – линейный размер слоя. Мы использовали алгоритм Метрополиса для обновления спиновых конфигураций. Моделирование проводилось при критической температуре TC = 1.15 для N = 3 монослоя (МС), Tc = 1.31 для N = 5 МС, TC = 1.39 для N = 7 МС [8–10] и различных начальных состояниях m0 = 1, m0 = 0.0001 $ \ll $ 1.

Эффективная константа анизотропии Δ(N) [8, 9] в зависимости от толщины пленки N была выбрана из экспериментальных исследований температуры Кюри TC для тонких пленок Ni(111)/W(110) [10] с различной толщиной пленки Ni. При этом максимальное значение критической температуры соответствует максимальному значению константы анизотропии Δ(N) = 1. При дальнейшем росте толщины пленки константа анизотропии стремится к нулю. В данной работе расчеты проводились для Δ(N = 3) = 0.636, Δ(N = 5) = 0.734, Δ(N = 7) = 0.816.

МОДЕЛИРОВАНИЕ ИЗ РАЗЛИЧНЫХ НАЧАЛЬНЫХ СОСТОЯНИЙ

Для изучения явлений старения были рассчитаны временные зависимости двухвременной автокорреляционной функции

(2)
$C(t,{{t}_{w}}) = \left\langle {\frac{1}{{{{N}_{s}}}}\sum\limits_i {{{{\vec {S}}}_{i}}(t)} {{{\vec {S}}}_{i}}({{t}_{w}})} \right\rangle - m(t)m({{t}_{w}}),$
где t – время, прошедшее с момента приготовления образца до измерения величины; m(t) – намагниченность, которая является параметром порядка для ферромагнитной пленки. На рис. 1 данные для C(t, tw) построены в зависимости от времени наблюдения t – tw для тонкой гейзенберговской пленки с толщиной N = 3 МС для различных значений времени ожидания tw = 200, 100, 70, 50, 20, 0 шагов Монте-Карло на спин (MCS/s). Моделирование проводилось при критической температуре из высокотемпературного начального состояния m0$ \ll $ 1 (рис. 1а) и низкотемпературного начального состояния m0 = 1 (рис. 1б).

Рис. 1.

Релаксация автокорреляционной функции C(t, tw) для пленки толщиной N = 3 МС при различных значениях времени ожидания tw = 200, 100, 70, 50, 20, 0 MCS/s из различных начальных состояний: высокотемпературного m0$ \ll $ 1 (а) и низкотемпературного m0 = 1 (б).

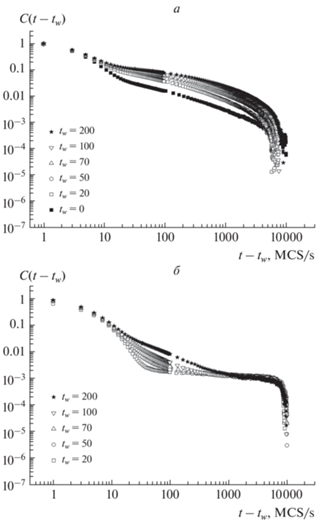
Автокорреляционная функция наглядно демонстрирует наличие трех характерных режимов: квазиравновесного режима в моменты времени (t – tw) $ \ll $ tw и неравновесного режима в моменты времени (t – tw) $ \gg $ tw. В моменты времени (t – tw) ~ ~ tw имеет место кроссоверный режим с зависимостью корреляционных характеристик от времени ожидания [11]. При меньших значениях времени tw автокорреляция быстро релаксирует до плато Ceq ~ $m_{{eq}}^{2}$ ~ t–2β/νz и только при больших значениях t – tw спадает до нуля. Более того, для разных значений tw данные характеризуются разными законами убывания, что означает нарушение временнóй инвариантности. Поведение автокорреляционной функция демонстрирует замедление процессов релаксации с увеличением tw. Так, например, автокорреляционная функция спадает со значения 1 до 0.01 для tw = 20 за 659 MCS/s, для tw = 50 за 1146 MCS/s, для tw = 70 за 1419 MCS/s, для tw = 100 за 1805 MCS/s, для tw =  200 за 2546 MCS/s при моделировании из высокотемпературного начального состояния m0 $ \ll $ 1 (рис. 1а). При моделировании из низкотемпературного начального состояния m0 = 1 релаксация автокорреляционной функции со значения 1 до 0.01 происходит быстрее для tw = 20 за 22 MCS/s, для tw = 50 за 26 MCS/s, для tw = 70 за 31 MCS/s, для tw = 100 за 40 MCS/s, для tw = 200 за 78 MCS/s (рис. 1б). Вместе с упомянутой выше медленной динамикой это нарушение временной инвариантности является вторым определяющим свойством стареющих систем. Таким образом моделирование динамического процесса из полностью упорядоченного состояния наиболее предпочтительно из-за меньшего влияния флуктуаций на результаты.

Для оценки времени корреляции наших систем мы рассчитываем безразмерную динамическую корреляционную функцию R(t, tw) [12] для различной толщины пленки N = 3, 5, 7 МС и для различного времени ожидания tw = 20, 50, 70, 100, 200 MCS/s:

(3)
$R(t,{{t}_{w}}) = \frac{{C(t,{{t}_{w}})}}{{\sqrt {\left[ {\left\langle {{{{\left( {\frac{1}{{{{N}_{S}}}}\sum\limits_{i = 1}^{{{N}_{S}}} {{{{\vec {S}}}_{i}}(t){{{\vec {S}}}_{i}}({{t}_{w}})} } \right)}}^{2}}} \right\rangle } \right]} }}.$

Зависимости безразмерной динамической корреляционной функции R(t, tw) от времени представлены на рис. 2а. При достаточно больших временах R(t, tw) убывает экспоненциально:

(4)
$R(t,{{t}_{w}})\sim \exp ({{ - t} \mathord{\left/ {\vphantom {{ - t} {{{\tau }_{{cor}}}}}} \right. \kern-0em} {{{\tau }_{{cor}}}}}).$
Рис. 2.

Безразмерная динамическая корреляционная функция R(t, tw) (а) для тонких пленок с N = 3 МС при различных временах ожидания tw= 200, 100, 70, 50, 20 MCS/s и соответствующая среднеквадратичная погрешность аппроксимации (б) от выбранного временного интервала.

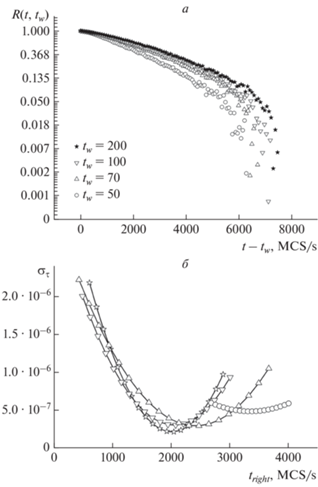
По наклону временной зависимости безразмерной динамической корреляционной функции R(t, tw) (рис. 2а) построенной в логарифмическом масштабе можно оценить значение времени корреляции τcor. Минимум среднеквадратичной погрешности аппроксимации (рис. 2б) для N = 3 достигается на интервале [700; tright] для tright = 2000 при tw = 200, для tright= 2000 при tw = 100, для tright = = 2400 при tw = 70 и для tright= 3500 при tw = 50.

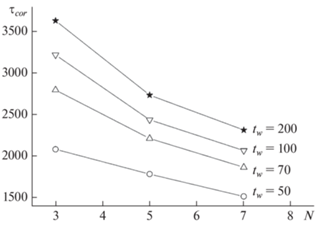
Значения времени корреляции представлены на рис. 3. Величина времени корреляции τcor демонстрирует наличие эффектов старения в тонких гейзенберговских пленках. Увеличение возраста системы tw приводит к увеличению значения τcor.

Рис. 3.

Зависимость времени корреляции от толщины пленки и времени ожидания.

В спиновых системах при фазовых переходах второго рода проявляются эффекты критического замедления, т.е. увеличение времени корреляции τcorпри приближении к критической точке Tc. Степенной характер асимптотической зависимости τcor определяется универсальным динамическим критическим показателем z:

(5)
${{\tau }_{{cor}}}\sim {{\left| {T - {{T}_{с}}} \right|}^{{ - \nu z}}},$
где ν – критический показатель корреляционной длины.

Для независимой оценки динамического критического индекса z в данной работе был проведен расчет кумулянта F2(t):

(6)
${{F}_{2}}(t) = \frac{{{{m}^{{(2)}}}(t)\left| {_{{{{m}_{0}} = 0}}} \right.}}{{{{m}^{2}}(t)\left| {_{{{{m}_{0}} = 1}}} \right.}}\sim {{t}^{{{d \mathord{\left/ {\vphantom {d z}} \right. \kern-0em} z}}}},$
где d – размерность системы.

Временная зависимость кумулянта F2(t) позволяет определить отношение d/z по углу наклона кривой, построенной в двойном логарифмическом масштабе. Были получены следующие значения данного отношения для различных толщин пленок d/z = 1.0224(2) для N = 3 МС, d/z = 1.0146(3) для N = 5 МС, d/z = 1.0985(2) для N = 7 МС.

Значение самого динамического критического индекса z было получено с использованием эффективной размерности системы deff, которая была получена из гиперскейлингового соотношения γ/ν + 2β/ν = deff. Используя значения статических критических индексов из [8] была найдена эффективная размерность системы deff= 2.007 (125) для пленок с толщиной N = 3 МС, deff = 1.992 (98) для пленок с толщиной N = 5 МС, deff = 2.158 (135) для пленок с толщиной N = 7 МС. Были получены соответствующие значения динамического критического индекса z = 1.827(99) для N = 3, z = = 1.963(192) для N = 5, z = 2.111(131) для N = 7. Таким образом пленки с толщиной N = 3, N = 5 демонстрируют критическое поведение, характерное для квазидвумерных систем.

ЗАКЛЮЧЕНИЕ

В критическом поведении тонких гейзенберговских пленках проявляются эффекты старения. На это указывает временное поведение автокорреляционной функции. С увеличением времени ожидания tw происходит замедление процессов релаксации в системах. Выполнена оценка времени корреляции. Увеличение возраста системы tw приводит к увеличению значения τcor. Величина времени корреляции τcor демонстрирует наличие эффектов старения в тонких гейзенберговских пленках.

При уменьшении размеров магнитных систем происходит усилением флуктуаций спиновой плотности и проявляются эффектов критического замедления. Таким образом эффекты старения проявляются в неравновесном поведении низкоразмерных магнитных систем.

Исследование выполнено при финансовой поддержке Министерства образования и науки Российской Федерации (договор 0741-2020-0002) и Совета по грантам Президента Российской Федерации (проект № МД-2229.2020.2). Вычислительные исследования поддержаны за счет ресурсов, предоставленных Центром коллективного обслуживания “ЦОД ДВО РАН” (Хабаровск) [13].

Список литературы

  1. Vélez S., Golovach V.N., Gomez-Perez J.M. et al. // Phys. Rev. B. 2019. V. 100. Art. No. 180401(R).

  2. Tang M., Zhao B., Zhu W. et al. // ACS Appl. Mater. Interfaces. 2018. V. 10. No. 5. P. 5090.

  3. Zanjani S.M., Onbaşlı M.C. // J. Magn. Magn. Mater. 2020. V. 499. Art. No. 166108.

  4. Arceri F., Landes F.P., Berthier L., Biroli G. Encyclopedia of complexity and systems science. Springer, 2021. P. 1.

  5. Baity-Jesi M., Calore E., Cruz A. et al. // Phys. Rev. Lett. 2018. V. 120. Art. No. 267203.

  6. Bag P., Baral P. R., Nath R. // Phys. Rev. B. 2018. V. 98. Art. No. 144436.

  7. Прудников В.В., Прудников П.В., Поспелов Е.А., Маляренко П.Н. // Письма в ЖЭТФ. 2018. Т. 107. № 9. С. 595; Prudnikov V.V., Prudnikov P.V., Pospelov E.A., Malyarenko P.N. // JETP Lett. 2018. V. 107. No. 9. P. 569.

  8. Прудников П.В., Прудников В.В., Медведева М.А. // Письма в ЖЭТФ. 2014. Т. 100. № 7. С. 501; Prudnikov P.V., Prudnikov V.V., Medvedeva M.A. // JETP Lett. 2014. V. 100. No. 7. P. 446.

  9. Prudnikov P.V., Menshikova M.A. et al. // J. Magn. Magn. Mater. 2015. V. 387. P. 77.

  10. Medvedeva M.A., Prudnikov P.V. // J. Phys. Conf. Ser. 2014. V. 510. Art. No. 012024.

  11. Prudnikov P.V., Prudnikov V.V., Krinitsyn A.S. et al. // Phys. Rev. E. 2010. V. 81. Art. No. 011130.

  12. Bhatt R.N., Young A.P. // Europhys. Lett. 1992. V. 20. No. 1. P. 59.

  13. Sorokin A.A., Makogonov S.V., Korolev S.P. // Sci. Tech. Inf. Process. 2017. V. 44. No. 4. P. 302.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал