Известия РАН. Серия географическая, 2021, T. 85, № 1, стр. 39-48
Моделирование морфологии междугородней сети автомобильных дорог
a Уральский государственный университет путей сообщения
Екатеринбург, Россия
b Институт экономики УрО РАН
Екатеринбург, Россия
* E-mail: amartynenko@rambler.ru
Поступила в редакцию 04.06.2020
После доработки 14.09.2020
Принята к публикации 30.10.2020
Аннотация
Многие аспекты функционирования транспортной сети и ее влияние на социально-экономическое развитие территории существенно зависят от ее морфологии. В частности, морфологические особенности сети лежат в основе сетевых эффектов, которые могут приводить к значительным изменениям транспортных затрат (как в сторону уменьшения, так и в сторону увеличения) при незначительных модификациях сети. Статья посвящена анализу факторов, наиболее значимых для морфологии междугородней транспортной сети, и математическому описанию механизмов реализации их влияния. Показано, что ключевым фактором является расположение вершин сети в пространстве, и предложено двухпараметрическое семейство моделей, позволяющих генерировать сети, близкие к реальным, только лишь на основе информации о пространственном расположении их вершин. Реализация предложенной модели продемонстрирована на примере междугородней сети автомобильных дорог Белоруссии. Для этой сети подобраны оптимальные значения параметров и показано, что полученная модель достаточно близка к исходной сети.
ВВЕДЕНИЕ
Функционирование транспортной сети и ее влияние на обслуживаемую территорию в значительной мере определяется ее топологической структурой, для обозначения которой обычно используют термины “начертание сети” или “морфология сети” [9].
Находясь на стыке географии, теории графов и инженерных задач по развитию транспортной инфраструктуры, морфология сети вызывает устойчивый научный интерес на протяжении по-следних десятилетий, что привело к появлению большого количества исследований в этой области. Один из основных подходов, применяемых для изучения транспортных сетей, заключается в том, что различные свойства сети (в том числе морфологические) описываются с помощью количественных характеристик, которые позволяют оценить взаимное влияние сети и обслуживаемой ею территории. По всей видимости, такой подход впервые был использован в 1960-е годы. К. Канским [14], который, рассматривая транспортную сеть как граф, предложил набор количественных характеристик сети (их теперь принято называть индексами Канского), имеющих высокий уровень корреляции с социально-экономическими показателями территории.
В дальнейшем индексы Канского и их модификации использовались многими зарубежными и отечественными исследователями (см., например, [1, 13] и обзорную работу [11]). Кроме того, работа К. Канского [14] дала мощный толчок исследованиям по конструированию количественных характеристик транспортной сети, позволяющих оценивать различные аспекты ее функционирования и влияния на территорию. Пережив некоторый спад в 1980-е годы, деятельность в этом направлении значительно активизировалась с конца 1990-х годов благодаря росту технических возможностей для расчета сложных сетевых характеристик [4, 6, 10] и тому, что анализ транспортных сетей начал использоваться как инструмент анализа инфраструктурных проектов [15] и программ территориального социально-экономического развития [12].
В перечисленных работах все многообразие транспортной сети сводится к набору числовых показателей, что приводит к значительной потере информации. Вместе с тем высокий уровень сложности транспортной сети делает практически невозможным ее непосредственное детальное описание и изучение и в любом случае требует определенного агрегирования ее морфологических свойств. Эффективный баланс между детализацией и агрегированием был достигнут С.А. Тарховым в [9]. Здесь для изучения сети были использованы морфологические субструктуры (циклы и дендриты), каждая из которых может состоять из десятков и сотен элементов. Такой подход позволил выявить фундаментальные закономерности эволюции транспортных сетей и сформулировать их в терминах самоорганизованного пространственного развития указанных субструктур. Разработанный в [9] исследовательский инструментарий был успешно применен к анализу многих реальных транспортных сетей (в последнее время в [5, 7, 8]).
Принципиально иной подход к исследованию транспортных сетей предлагается в [16–18] (см. также цитированную в них литературу). В этих работах для изучения транспортных сетей используется моделирование их естественного развития. Основная идея предложенных моделей заключается в следующем. Процесс развития сети разбивается на дискретные шаги, и на каждом шаге пользователи сети по определенным правилам формируют спрос на создание новых элементов сети. Если спрос высокий, то на следующем шаге соответствующий элемент создается, а если спрос на какой-то из существующих элементов низкий, то он удаляется. Полученные таким образом сети обладают многими свойствами реальных сетей (иерархичность структуры, самоорганизация и т.д.). Отметим, что существенным преимуществом использования моделирования является возможность работать с исходной сетью без значительного упрощения ее структуры (уровень детализации лимитируется только мощностью используемого компьютера).
Различные аспекты функционирования сети не сводятся только лишь к ее морфологии. Для полного описания сети важны свойства ее отдельных элементов (длина, количество полос, ширина проезжей части, качество дорожного покрытия и т.д.), которые могут быть сведены к нескольким числовым характеристикам. Например, к пропускной способности элемента и к (обобщенной) стоимости перемещения по нему. В качестве последней может выступать как непосредственно стоимость, так и время или расстояние, а также различные комбинации этих величин. Стоимость перемещения по каждому из элементов сети, наряду с ее морфологией, определяет маршруты наименьшей стоимости, по которым транспортные средства перемещаются между различными парами вершин.
Важность исследования именно морфологии сети (без учета характеристик ее элементов) обусловлена следующими соображениями. Стоимость перемещения по элементу сети непосредственно зависит от затрат на его обслуживание и развитие. При этом изменение отдельного элемента оказывает лишь локальное влияние на функционирование сети (изменение стоимости проезда между двумя любыми вершинами, полученное в результате изменения одного элемента сети, не превосходит изменения стоимости перемещения по этому элементу).
В отличие от стоимости перемещения по элементам сети морфологические свойства сети не зависят напрямую от затрат на ее создание и содержание в том смысле, что при одинаковых затратах могут быть получены две сети с существенно различной морфологией. Это вызвано тем, что затраты на сеть зависят от ее общей протяженности, характера рельефа, климата и степени освоенности территории, а не от морфологической структуры сети. При этом изменение морфологии может оказывать влияние на стоимость перемещения по сети вследствие возникновения так называемого сетевого эффекта, который заключается в том, что совокупность морфологических изменений сети может давать результат, превышающий сумму результатов, получаемых от каждого изменения в отдельности. Например, создание двух новых элементов сети может приводить к снижению стоимости перемещения между некоторыми вершинами на величину, которая будет превышать сумму снижений этой стоимости, получаемых в результате создания каждого из этих элементов в отдельности. В научной литературе сетевой эффект также называют эмерджентностью [18] или супераддитивностью [2] транспортной сети.
ПОСТАНОВКА ПРОБЛЕМЫ
Основной вопрос, возникающий при исследовании транспортных сетей, можно сформулировать так: почему транспортная сеть такая, как она есть? В более строгой и, возможно, самой сильной постановке его можно переформулировать следующим образом: что собой представляют универсальные закономерности (механизмы, алгоритмы, правила и т.п.), которые определяют, какие из всех потенциально возможных элементов сети будут существовать (и какими из всех потенциально возможных характеристик они будут обладать), а какие не будут существовать при всех возможных комбинациях всех факторов, влияющих на формирование сети? Если бы мы знали ответ на этот вопрос, то это означало бы, что, имея для некоторой территории всю необходимую информацию о всех необходимых факторах, мы могли бы однозначно восстановить сеть, обслуживающую эту территорию.
Естественно, в таком виде вопрос является чрезвычайно сложным и малопригодным для содержательного исследования, однако его удобно использовать в качестве отправной точки для дальнейшего упрощения и конкретизации исследуемой проблемы.
В настоящей работе мы упростим указанный вопрос по нескольким направлениям. Во-первых, мы не будем учитывать характеристики отдельных элементов сети, т.е. будем рассматривать только морфологию сети. Во-вторых, мы не будем требовать, чтобы искомые закономерности однозначно детерминировали все элементы сети. Вместо этого мы будем говорить о закономерностях, которые определяют сеть, близкую по тем или иным свойствам к реальной сети, но не обязательно полностью совпадающую с ней. Отметим, что результаты именно такого типа были получены в [9]: установленные там закономерности не предсказывают развитие сети с точностью до всех ее отдельных элементов, а задают все ее возможные состояния в виде набора сетей, удовлетворяющих определенным свойствам. Наконец, мы не будем стремиться к тому, чтобы учесть все возможные факторы, влияющие на сеть, а попытаемся выделить среди них наиболее важные, которые определяют сущностные свойства сети.
Изучению влияния различных факторов на развитие транспортной сети посвящено много исследований. Краткий обзор полученных результатов можно найти в [9]. Там же приводится объемный перечень факторов, которые объединяются в 10 групп. С точки зрения моделирования сети все эти факторы удобно классифицировать следующим образом:
1) факторы, связанные с неоднородностью пространства (рельеф, речная сеть, форма территории, границы государств и т.п.);
2) факторы, связанные с неоднородностью вершин сети (людность населенных пунктов, являющихся вершинами сети, их экономическое развитие, промышленное производство, обеспеченность ресурсами и т.п.);
3) взаимное расположение вершин сети в пространстве.
Факторы из первой группы влияют только на затраты, необходимые для создания и содержания элементов сети. Факторы из второй группы влияют только на “спрос на связность”, т.е. на потребность вершин сети в существовании соединяющих их элементов. Третья группа состоит из одного фактора. Он не связан с неоднородностью пространства и вершин, но оказывает влияние как на затраты (чем больше расстояние между вершинами, тем больше затраты на строительство дороги между ними), так и на спрос (для близко расположенных вершин спрос на связность выше, чем для удаленных).
Если бы на сеть действовали только факторы из первой группы, т.е. если бы полностью отсутствовал спрос на связность, сеть бы вовсе не существовала. Если бы на сеть действовали только факторы из второй группы, т.е. если бы строительство и содержание дорог вообще не требовало затрат, сеть представляла бы собой полный граф (каждая пара вершин соединялась дорогой по кратчайшему расстоянию). Другими словам, действие каждой из первых двух групп факторов приводит к тривиальному результату.
Реальная сеть – это результат достижения равновесия (неустойчивого) между затратами и спросом, а взаимное расположение вершин – это единственный фактор, который влияет как на затраты, так и на спрос. Если на сеть будет действовать только лишь этот фактор, этого уже достаточно для возникновения сети с нетривиальной морфологией. В этом смысле взаимное расположение вершин является основным фактором развития сети.
Продолжая уточнять сформулированный выше вопрос, отметим, что закономерностям, о которых в нем идет речь, можно придать различную форму. В частности, ответ может быть представлен в виде модели, генерирующей транспортную сеть по некоторым исходным данным. Далее в качестве таких данных мы будем использовать информацию о взаимном расположении вершин сети.
МЕТОДЫ И МАТЕРИАЛЫ
Любую реальную междугороднюю транспортную сеть будем отождествлять с графом G = (V, E), где V – множество вершин сети, E – множество дуг, соединяющих вершины сети. В качестве вершин сети выступают населенные пункты и пересечения (примыкания) дорог. Поскольку нас интересует только взаимное расположение вершин, далее мы не будем использовать какую-либо информацию о вершинах сети, кроме их координат. Также мы не учитываем характеристики отдельных дуг сети, поэтому мы будем считать, что все дуги обладают неограниченной пропускной способностью, и длина любой дуги равна расстоянию по воздуху между вершинами, которые она соединяет.
Под моделью реальной сети G* мы далее будем понимать сеть G* = (V, E*), в которой множество вершин V такое же, как в сети G, а множество дуг E* генерируется с помощью некоторого условия. Такое условие является ключевым элементом модели и, если она достаточно близка к реальной сети, указанное условие можно рассматривать как искомую внутреннюю закономерность формирования сети. Очевидно, что для выбора такого условия существует много возможностей и более сложные условия обеспечивают более точные модели. В то же время компьютерная реализация моделей реальных сетей требует весьма значительных вычислительных ресурсов, и для сложных условий генерирование сети может быть не реализуемым. Поэтому в данной работе предлагается не очень сложное условие, которое допускает компьютерную реализацию за приемлемое время и при этом получающаяся модель достаточно точно описывает реальную сеть. Итак, дуги модели будут определяться следующим образом: каковы бы ни были вершины ${{{v}}_{1}},{{{v}}_{2}} \in V,$ множество $E* = E{\text{*}}\left( {a,~b} \right)$ содержит дугу $\left( {{{{v}}_{1}},{{{v}}_{2}}} \right)$ тогда и только тогда, когда для любой вершины $w \in V,$ отличной от ${{{v}}_{1}}$ и ${{{v}}_{2}},$ выполняется неравенство:
(1)
$\begin{gathered} a\max \left\{ {d\left( {{{{v}}_{1}},w} \right),d\left( {{{{v}}_{2}},w} \right)} \right\} + \\ + \,\,b\min \,\,\left\{ {d\left( {{{{v}}_{1}},w} \right),\,\,\,\,d\left( {{{{v}}_{2}},w} \right)} \right\} > d\left( {{{{v}}_{1}},{{{v}}_{2}}} \right), \\ \end{gathered} $Предложенное условие (1) является одним из возможных вариантов строгой формулировки простого эмпирического наблюдения, справедливого для реальных сетей: если вблизи от середины отрезка, соединяющего вершины ${{{v}}_{1}}$ и ${{{v}}_{2}},$ есть другие вершины сети, то в большинстве случаев вершины ${{{v}}_{1}}$ и ${{{v}}_{2}}$ не соединяются дугой. Если же все остальные вершины находятся далеко от середины отрезка, соединяющего вершины ${{{v}}_{1}}$ и ${{{v}}_{2}},$ то в большинстве случаев вершины ${{{v}}_{1}}$ и ${{{v}}_{2}}$ соединяются дугой. Связь этого наблюдения с условием (1) становится понятной, если обратить внимание на то, что в левой части неравенства (1) стоит взвешенная сумма расстояний от вершины w до вершин ${{{v}}_{1}}$ и ${{{v}}_{2}}.$ В частности, в самом простом случае a = b условие (1) превращается в неравенство:
(2)
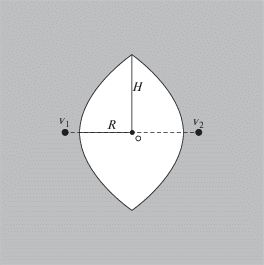
$d\left( {{{{v}}_{1}},w} \right) + d\left( {{{{v}}_{2}},w} \right) > \frac{1}{a}d\left( {{{{v}}_{1}},{{{v}}_{2}}} \right),$На рис. 1 показана графическая интерпретация условия (1): если все остальные вершины лежат в серой области, то вершины ${{{v}}_{1}}$ и ${{{v}}_{2}}$ соединяются дугой в сети G*, а если хотя бы одна вершина лежит в незакрашенной области, то дуги между ${{{v}}_{1}}$ и ${{{v}}_{2}}$ нет. Незакрашенная область на рис. 1 получена при a = 1.1 и b = 0.2. Она представляет собой выпуклую центральносимметричную фигуру с центром в точке О – середине отрезка ${{{\text{v}}}_{1}}{{{\text{v}}}_{2}}.$ Данную фигуру можно охарактеризовать величинами R и H, показанными на рис. 1. Эти величины связаны с параметрами a и b следующими формулами:
(3)
$\begin{gathered} a = \\ = \frac{{2d\left( {{{{v}}_{1}},{{{v}}_{2}}} \right)\left( {\left| {d\left( {{{{v}}_{1}},{{{v}}_{2}}} \right) - 2R} \right| - \sqrt {4{{H}^{2}} + d{{{\left( {{{{v}}_{1}},{{{v}}_{2}}} \right)}}^{2}}} } \right)}}{{\sqrt {4{{H}^{2}} + d{{{\left( {{{{v}}_{1}},{{{v}}_{2}}} \right)}}^{2}}} \left( {\left| {d\left( {{{{v}}_{1}},{{{v}}_{2}}} \right) - 2R} \right| - d\left( {{{{v}}_{1}},{{{v}}_{2}}} \right) - 2R} \right)}}, \\ \end{gathered} $(4)
$\begin{gathered} b = \\ = \frac{{2d\left( {{{{v}}_{1}},{{{v}}_{2}}} \right)\left( {\sqrt {4{{H}^{2}} + d{{{\left( {{{{v}}_{1}},{{{v}}_{2}}} \right)}}^{2}}} - d\left( {{{{v}}_{1}},{{{v}}_{2}}} \right) - 2R} \right)}}{{\sqrt {4{{H}^{2}} + d{{{\left( {{{{v}}_{1}},{{{v}}_{2}}} \right)}}^{2}}} \left( {\left| {d\left( {{{{v}}_{1}},{{{v}}_{2}}} \right) - 2R} \right| - d\left( {{{{v}}_{1}},{{{v}}_{2}}} \right) - 2R} \right)}}. \\ \end{gathered} $Для выбора значений параметров a и b, обеспечивающих наибольшую близость модели к реальной сети, нам необходима мера различия (или сходства) двух сетей с одинаковым набором вершин. Для измерения различия двух объектов существуют различные подходы, каждый из которых обладает определенными достоинствами и недостатками. В настоящей работе в качестве меры различия сетей G и G* будем использовать меру
(5)
$\varphi \left( {G,G{\text{*}}} \right) = \frac{{{\text{||}}S\left( G \right)--S{\text{(}}G{\text{*)|}}{{{\text{|}}}_{1}}}}{{{\text{||}}S\left( G \right){\text{|}}{{{\text{|}}}_{1}}}},$Введенная таким образом мера $\varphi \left( {G,G{\text{*}}} \right)$ отражает функциональное различие двух сетей. С точки зрения потребителя транспортных услуг две сети будут обладать сходством, если они одинаковым образом выполняют функцию по обеспечению транспортных потребностей вершин, т.е. если будут близки затраты на перемещения между вершинами сети. А это равносильно тому, что две сети будут иметь мало отличающиеся кратчайшие пути для всех пар вершин. Соответственно, если кратчайшие пути для всей совокупности вершин сильно различаются для исходной и модельной сетей, это означает, что сети сильно различаются с точки зрения своего функционирования.
Мера (5) является аналогом относительной погрешности: выражение в ее знаменателе – это затраты на перемещения между всеми вершинами реальной сети, а в числителе – разность между такими затратами для реальной сети и модели. Мера φ(G, G*) принимает неотрицательные значения. Если G и G* полностью совпадают, то φ(G, G*) = 0, а чем значительнее их отличия, тем больше значение φ(G, G*).
Как уже было сказано выше, на морфологию сети влияют три группы факторов. Поэтому для наиболее наглядной демонстрации возможностей описанного подхода нам необходима сеть, на формирование которой неоднородность пространства и вершин оказывают как можно меньшее влияние по сравнению с влиянием взаимного расположения вершин. Хорошим кандидатом на эту роль является сеть автомобильных дорог Белоруссии, поскольку эта страна имеет компактную и достаточно однородную территорию без существенных естественных преград, а неоднородность вершин (городов) хорошо коррелирует с их пространственным расположением (это снижает влияние неоднородности вершин как самостоятельного фактора).
В качестве исходных данных мы использовали материалы сайта11 (векторные слои автомобильных дорог и городов в формате shp на основе данных проекта OpenStreetMap). Эти данные чрезмерно детализированы для целей данной статьи, поэтому мы удалили все внутригородские дуги, а также выполнили ряд других незначительных преобразований сети (более подробное описание подобных преобразований можно найти в [3, 4]). В итоге получили сеть с 10 167 дугами и 6560 вершинами, из которых 4140 являются населенными пунктами (рис. 2а). При таком количестве вершин требуются очень существенные вычислительные мощности для построения модели и подбора оптимальных значений параметров (количество операций, необходимое для получения модели при конкретных значениях параметров a и b, пропорционально n3, где n – количество вершин).
Рис. 2.
Сеть автомобильных дорог Белоруссии: (а) исходная; (б) упрощенная (удалены дуги, обслуживающие малозначительные вершины).
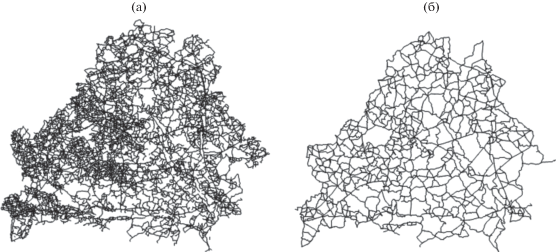
Значительная часть вершин рассматриваемой сети – это висячие вершины, являющиеся малолюдными населенными пунктами, а также вершины, в которых дуги, идущие от этих висячих вершин, соединяются с остальной сетью. Очевидно, что такие вершины не оказывают значимого влияния на остальную сеть. Поэтому можно упростить сеть без потери ее основных морфологических свойств за счет выделения основной части сети, соединяющей все населенные пункты, людность которых превышает 1000 чел. (таких пунктов насчитывается 444). В эту часть мы включаем все дуги сети, принадлежащие хотя бы одному из кратчайших путей между всеми возможными парами рассматриваемых населенных пунктов. В итоге получается сеть c 1131 дугой и 626 вершинами, представленная на рис. 2б. Именно для этой сети будет далее построена модель в соответствии с условием (1).
Обработка исходных данных и создание моделей осуществлялось в среде Wolfram Matemathica 11, использование которой для работы с геоданными детально описано в [3].
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
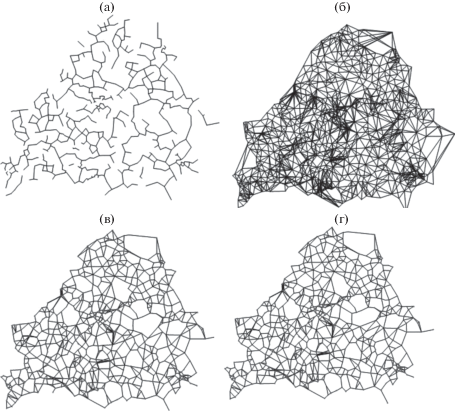
В зависимости от значений параметров a и b на основе правила (1) можно сгенерировать существенно различные модели сети автомобильных дорог, изображенной на рис. 2б. Некоторое представление о многообразии возможных моделей можно получить из рис. 3. В частности, на рис. 3а изображена “бедная” модель, которая содержит значительно меньше дуг, чем реальная сеть. Значение меры различия для этой модели и реальной сети равно φ = 1.02. На рис. 3б изображена “богатая” сеть. Соответствующее ей значение меры различия равно φ = 0.08. Обе модели сильно отличаются от реальной сети и, более того, они крайне нереалистичны: первая демонстрирует явный дефицит циклов при чрезмерно ветвящихся дендритах и большом количестве компонент связности, в то время как вторая не является планарным графом и содержит очень много трехвершинных циклов22.
Рис. 3.
Модели сети автомобильных дорог Белоруссии: (а) при a = 1 и b = –0.11; (б) при a = 1.2 и b = 0.3; (в) при a = 1.164 и b = –0.007; (г) при a = 1.169 и b = 0.0.
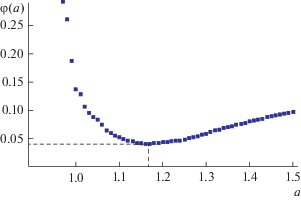
Чтобы получить модель, наиболее близкую к реальной сети, необходимо минимизировать функцию φ(a, b). Эта функция является разрывной и многоэкстремальной, поэтому для оптимизации мы применили метод перебора33. Перебор осуществлялся по сетке с шагом 0.01 для значений r и h из прямоугольника {0.2 ≤ r ≤ 1.2, 0.2 ≤ h ≤ 2}. По этим значениям вычислялись a и b с помощью формул (3) и (4), а по ним, в свою очередь, рассчитывалось значение функции φ(a, b). Значения функции φ(a, b) для некоторых значений ее аргументов представлены в табл. 1. Если исходить из визуализации, представленной на рис. 1, то можно сказать, что перебор был выполнен по незакрашенным областям для всех возможных пар R и H из указанного выше прямоугольника. В результате получили φmin = 0.040 при amin = 1.164 и bmin = = –0.007. Модель, соответствующая этим значениям, представлена на рис. 3в.
Таблица 1.
Значения меры φ(a, b)
| Значениe параметров | Значение меры | |
|---|---|---|
| a | b | |
| 1.078 | 0.883 | 0.108 |
| 1.877 | –0.757 | 0.105 |
| 3.057 | –2.086 | 0.082 |
| 0.911 | –0.016 | 0.981 |
| 1.138 | –0.244 | 0.267 |
Полученное значение ${{b}_{{{\text{min}}}}}$ во много раз меньше, чем ${{a}_{{{\text{min}}}}}$ (${{{{a}_{{{\text{min}}}}}} \mathord{\left/ {\vphantom {{{{a}_{{{\text{min}}}}}} {{{b}_{{{\text{min}}}}}}}} \right. \kern-0em} {{{b}_{{{\text{min}}}}}}} \approx 166$), т.е. второй член в левой части условия (1) практически не оказывает влияния на конечный результат. Кроме этого, значение ${{b}_{{{\text{min}}}}}$ является отрицательным, что затрудняет (хотя и не исключает) его содержательную интерпретацию. Поэтому достаточно естественно рассмотреть более простую модель сети с условием (1) при b = 0, т.е. модель, в которой существование дуги $\left( {{{{v}}_{1}},{{{v}}_{2}}} \right)$ определяется условием
(6)
$a\max \left\{ {d\left( {{{{v}}_{1}},w} \right),d\left( {{{{v}}_{2}},w} \right)} \right\} > d\left( {{{{v}}_{1}},{{{v}}_{2}}} \right).$Модель сети, соответствующая оптимальному значению параметра a, представлена на рис. 3г. Хорошо видно, что сети на рис. 3в и 3г практически не имеют отличий, что еще раз подтверждает адекватность выполненной редукции.
Модельная сеть на рис. 3г выглядит достаточно реалистично (за исключением сгущений дуг в нескольких местах она не имеет визуально идентифицируемых особенностей, которые были бы несвойственны реальным сетям). Этот факт сам по себе представляет значительный интерес, поскольку он означает, что на основании условия (6) можно генерировать реалистичные сети. Однако нас в первую очередь интересует то, насколько полученная модель близка к реальной сети автомобильных дорог Белоруссии, изображенной на рис. 2б. В этом вопросе мы не можем полагаться на наблюдаемое визуальное сходство двух этих сетей, поскольку оно может быть следствием только лишь реалистичности модели и того, что любые реалистичные сети, имеющие высокую плотность дуг и связывающие одни и те же вершины, выглядят похожими. По причине высокой плотности дуг в реальной сети и в модели мы также не можем рассматривать относительно небольшое значение ${{\varphi }_{{{\text{min}}}}} = 0.041$ как существенное подтверждение близости модели и реальной сети. Очевидно, что в сетях с высокой плотностью дуг кратчайшие пути между вершинами не могут значительно отличаться своей протяженностью, и поэтому матрица кратчайших расстояний модели будет близка к матрице кратчайших расстояний реальной сети. Мера φпозволяет сравнивать разные модели с точки зрения их близости к реальной сети, однако конкретное значение ${{\varphi }_{{{\text{min}}}}}~$ не очень информативно.
Для того чтобы убедиться в близости модели и реальной сети, рассмотрим следующие совокупности:
$E\backslash E{\text{*}}$ – совокупность всех дуг реальной сети, не являющихся дугами модели; $E \cap E{\text{*}}$ – совокупность всех дуг общих для реальной сети и для модели;  – совокупность всех дуг модели, не являющихся дугами реальной сети. Количественные
характеристики этих совокупностей даны в табл. 2, а их визуализация представлена на рис. 5
.
– совокупность всех дуг модели, не являющихся дугами реальной сети. Количественные
характеристики этих совокупностей даны в табл. 2, а их визуализация представлена на рис. 5
.
Таблица 2.
Сравнение реальной сети и модели
| Совокупность дуг | Количество элементов |
|---|---|
| E | 1131 |
| E* | 1283 |
| $E{\backslash }E{\text{*}}$ | 250 |
| $E \cap E{\text{*}}$ | 881 |
 |
402 |
Рис. 5.
Сравнение реальной сети и модели, соответствующей оптимальному значению amin = 1.167: (а) дуги реальной сети, не являющиеся дугами модели; (б) дуги, общие для реальной сети и модели; (в) дуги модели, не являющиеся дугами реальной сети.
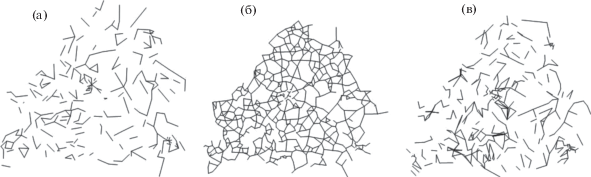
Из данных, представленных в табл. 2 , следует, что доля дуг, являющихся общими для модели и реальной сети, значительно превосходит как долю дуг реальной сети, не генерируемых моделью, так и долю дуг модели, не существующих в реальной сети: 881/1131 = 78% и 881/1283 = 69% против 250/1131 = 22% и 402/1283 = 31%. Полученные значения могут быть интерпретированы следующим образом: модель правильно предсказывает наличие дуги между вершинами для 78% дуг реальной сети. Однако 31% дуг, сгенерированных моделью, не существуют в реальной сети. Таким образом, модель демонстрирует некоторую асимметричность: ошибок, связанных с генерированием несуществующих дуг больше, чем ошибок, связанных с тем, что реально существующие дуги не генерируются моделью. По всей видимости, это является непосредственным следствием того, что в модели не учитывается рельеф, водные преграды и т.п., поскольку во многих случаях именно такие факторы имеют решающее значение при принятии решения о строительстве дороги.
Приведенные в табл. 2 количественные результаты можно дополнить рис. 5 . В частности, на рис. 5 а хорошо видно, что совокупность дуг $E \cap E{\text{*}}$ содержит основную информацию о морфологии реальной сети, в то время как “остатки” модели на рис. 5 а и 5в представляют собой случайные наборы дуг, равномерно распределенных по территории, которую обслуживает сеть, т.е. “остатки” не содержат структурно важной информации.
Таким образом, построенная модель основана на чрезвычайно простом условии (6) и использует только лишь информацию о взаимном расположении вершин, однако при этом она очень близка к реальной сети.
ЗАКЛЮЧЕНИЕ
Непосредственным следствием выполненного моделирования является тот факт, что для конкретной транспортной сети автомобильных дорог Белоруссии взаимное расположение вершин оказывает значимое влияние на морфологию сети, причем в качестве механизма реализации этого влияния можно рассматривать достаточно простое условие (6). На наш взгляд, этот результат создает хорошие предпосылки для дальнейших исследований по нескольким направлениям.
Во-первых, предложенные условия в виде (6) или (1) можно использовать для моделирования других сетей (для других территорий и других видов наземного транспорта). Если модели для других сетей будут иметь такое же высокое качество, как и модель, полученная в данной работе, то тем самым мы сведем все морфологические свойства сети к значению одного (в случае условия (6)) или двух (в случае условия (1)) параметров. Это, в свою очередь, позволит классифицировать транспортные сети на основе указанных параметров.
Во-вторых, несмотря на высокое качество полученной модели, она может быть улучшена. Очевидно, что влияние взаимного расположения вершин на морфологию сети не исчерпывается только лишь соотношением (1). По всей видимости, его можно дополнить другими условиями так, чтобы модель была еще ближе к реальной сети. Например, на рис. 5 в присутствуют скопления дуг, не характерные для реальных сетей, и они могут быть исключены путем введения некоторого дополнительного условия, запрещающего такие скопления для группы близких вершин.
Третье направление исследований связано с разработкой моделей более высокого качества за счет учета не только взаимного расположения вершин, но и других факторов, влияющих на сеть (неоднородность пространства и вершин). Например, необходимость в использовании информации о неоднородности вершин становится очевидной, если сравнить вид модели и реальной сети в окрестности Минска. Для формирования реальной транспортной сети политические и социально-экономические характеристики столицы Белоруссии играют основную роль по сравнению со всеми другими факторами, но построенная нами модель учитывает только взаимное расположение вершин, и поэтому она сильно отличается от реальной сети вблизи Минска.
Построенную в данной работе модель мы рассматриваем как отправную точку для дальнейших исследований в соответствии с перечисленными направлениями.
Список литературы
Бугроменко В.Н. Транспорт в территориальных системах. М.: Наука, 1987. 112 с.
Лившиц В.Н., Белоусова Н.И., Бушанский С.П., Васильева Е.М., Гук С.Н. Анализ динамики технологических детерминант естественно-монопольных транспортных сетей при оптимальном их развитии // Аудит и финансовый анализ. 2011. № 4. С. 138–159.
Мартыненко А.В. Программа Wolfram Mathematica как универсальная среда для обработки и анализа географической информации // Географический вестн. 2016. № 4. С. 129–138.
Мартыненко А.В., Петров М.Б. Влияние начертания транспортной сети на показатели доступности (на примере Свердловской области) // Региональные исследования. 2016. № 2. С. 21–30.
Панов Р.Д. Эволюция пространственной структуры сетей крупнейших метрополитенов мира // Изв. РАН. Сер. геогр. 2020. № 1. С. 20–26.
Селиверстов С.А. Разработка показателей транспортной обеспеченности // Изв. Петербургского ун-та путей сообщения. 2015. № 4. С. 48–63.
Тархов С.А. Анализ топологических дефектов сухопутной транспортной сети регионов Сибири и Дальнего Востока // Региональные исследования. 2019. № 3. С. 53–62.
Тархов С.А. Пространственные закономерности роста высокоскоростных железных дорог в мире // Региональные исследования. 2016. № 4. С. 90–104.
Тархов С.А. Эволюционная морфология транспортных сетей. Смоленск: Универсум, 2006. 386 с.
Aldous D., Shun J. Connected spatial networks over random points and a route-length statistic // Stat. Sci. 2010. V. 25. № 3. P. 275–288.
Barthelemy M. Spatial networks // Phys. Rep. Review Section of Phys. Lett. 2011. V. 499. № 1. P. 1–101.
Böhme K., Toptsidou M., Holstein F., Martin D. Territorial cooperation for the future of Europe. Luxembourg: ESPON, 2017. 104 p.
Haggett P., Chorley R. Network Analysis in Geography. London: Edward Arnold, 1969. 348 p.
Kansky K. Structure of transportation networks: relationships between network geometry and regional characteristics. Chicago: Univ. of Chicago Press, 1963. 155 p.
Nes R. Design of multimodal transport networks: a hierarchical approach (Ph.D. thesis). Delft: Technical Univ. of Delft, 2002. 304 p.
Xie F., Levinson D. Topological evolution of surface transportation networks // Comput. Environ. Urban Syst. 2009. V. 33. № 3. P. 211–223.
Yerra B., Levinson D. The emergence of hierarchy in transportation networks // Ann. Reg. Sci. 2005. V. 39. № 3. P. 541–553.
Zhang L., Levinson D. A model of the rise and fall of roads // J. Transport and Land Use. 2017. V. 10. № 1. P. 337–356.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия географическая