Известия РАН. Серия географическая, 2021, T. 85, № 2, стр. 165-175

ПОСТАНОВКА ПРОБЛЕМЫ

Классическая теория центральных мест (ТЦМ) – один из немногих формализованных конструктов общественной географии – подвергается критике за абстрактность постулатов (Johnston, 2007) и ошибки в исходных положениях (Nicolas, 2009). В то же время ТЦМ стала базисом (Мазаев, 2010), во-первых, для планов освоения (Rössler,1989) оккупированных нацистской Германией территорий современных Польши, Чехии и Словакии и, во-вторых, для Генеральной схемы расселения СССР (Наймарк, 1997), предложенной отечественными специалистами. В этой связи ТЦМ сохраняет свою актуальность до настоящего времени, а ее модификации могут быть использованы в качестве теоретической основы нового варианта Стратегии пространственного развития Российской Федерации на период после 2025 г.

Действительно, ошибки в расчетах встречаются даже у крупнейших математиков своего времени. Один из наиболее ярких примеров наших дней – доказательство в середине 1990-х годов Великой теоремы Ферма Эндрю Уайлсом, когда после, казалось бы, окончательного решения, представленного на одной из конференций, коллеги указали автору на существенный недостаток, который он исправил годом позже с помощью своего ученика; вспоминая об этих событиях в рамках интервью, Уайлс разрыдался перед камерой (Стюарт, 2019). Тем не менее наличие ошибок в доказательстве отдельных положений ТЦМ – это безусловный положительный момент, поскольку и ошибочный путь может приводить новых исследователей к исправлению недочетов и развитию самой теории. Поэтому ошибками подобные моменты мы не считаем (это очень важно в аспекте того, о чем будет идти речь далее).

Слабые места в аргументации положений ТЦМ зачастую связаны с абстрактным моделированием. Действительно, очень часто ТЦМ представляется конструктом, далеким от реальности, хотя, забегая вперед, повторим известное высказывание А. Лёша, что “сравнения нужны не для проверки теории, а для проверки действительности. Мы должны удостовериться в том, что существующее целесообразно” [цит. по: (Шупер, 2006)]. В то же время отечественная и зарубежная историография ТЦМ представлена только публикациями, посвященными отдельным ее направлениям; работы, охватывающие весь период развития теории, отсутствуют (Sonis, 2005). Изучение истории формирования ТЦМ как таковой будет способствовать не только выявлению сильных и нивелированию слабых сторон теории, но и предложению новых ее модификаций. Последние представляют собой новый вызов ТЦМ в условиях необходимости приближения теоретических построений к их реальным аналогам в рамках непосредственно существующих систем расселения (Гранберг, 2006).

МАТЕРИАЛЫ ИССЛЕДОВАНИЯ

Позволим себе напомнить аксиомы ТЦМ. Их формулировка в разных работах может звучать по-разному, однако суть от этого не меняется. Всего таких аксиом пять. Хотя В.А. Шупер (1995) предложил шестую аксиому, мы склонны относить ее скорее к категории теорем, поэтому здесь не упоминаем:

1) пространство однородно и изотропно во всех отношениях, за исключением распределения городского населения;

2) пространство бесконечно;

3) “части” системы центральных мест расположены максимально компактно;

4) системы центральных мест полиморфны (K = 3, K = 4, K = 7);

5) поведение потребителя “рационально”.

Курсивом в перечне выше выделены те части аксиом, которые мы бы хотели трансформировать, придав им более “приземленный”, иногда даже практический характер. Четвертая аксиома выделена полужирным шрифтом, поскольку ранее в работах исследователей была установлена возможность существования систем центральных мест (ЦМ) и другой структуры. Вероятно, для случаев K = 5 и K = 6 данное положение было доказано зарубежными (Church, Bell, 1990), а для K = 2 – отечественными (Важенин, 1997; Важенин, 2006) исследователями.

Пятая и вторая аксиомы в определенной степени связаны между собой и в единой трактовке приводят к очень интересному выводу о невозможности извлечения сверхприбыли поставщиками услуг в системах центральных мест; на этот факт указывал еще А. Лёш (Lösch, 1940). Этот вывод означает, что в решетке одно ЦМ более низкого уровня должно иметь возможность обслуживаться по крайней мере двумя ЦМ предшествующего – более высокого – уровня. Данное утверждение избыточно, если мы безоговорочно принимаем вторую аксиому, однако если же мы хотим трансформировать последнюю, то оно необходимо.

Отметим, что в нашем исследовании мы говорим прежде всего об иерархической, а не экономической составляющей в аспекте принципа дополнительности, предложенного В.А. Шупером (1996); хотя и будем к экономической составляющей время от времени обращаться. Указанный принцип заключается в том, что мы не можем для некой существующей системы ЦМ одновременно зафиксировать и их иерархию по численности населения, и совокупность центральных функций по обслуживанию себя и дополняющих районов. Тем не менее, две этих составляющих формирования решетки неразрывно друг с другом связаны, отделить их невозможно. В то же время, если мы желаем проследить путь эволюции этой системы ЦМ, преобладание той или иной составляющей в цепочке умозаключений исследователя приведет к совершенно разным схемам этой эволюции.

Разумеется, эволюционные процессы в системах расселения интересовали специалистов по ТЦМ, начиная со времени ее появления (Christaller, 1933). Классических экономгеографов в большей степени интересует иерархическая составляющая “принципа дополнительности” в отношении эволюции систем ЦМ. В то же время первые работы, посвященные этой проблеме, появились лишь в 1990-е годы благодаря экономистам. Причем были выполнены они в русле “новой экономической географии”: не удивительно при этом, что именно составляющая центральных функций была основной. Так, М. Фуджита, П. Кругманом и Т. Мори (Fujita et al., 1999) представлена схема эволюции участка сети ЦМ: она достаточно сложна, однако характерной чертой является то, что после ЦМ 1-го уровня возникает ЦМ не 2-го, а 3-го уровня. Это не удивительно, поскольку, с одной стороны, ЦМ 2-го уровня обслуживает бо́льшую территорию, а с другой, расположено слишком далеко (дальше ЦМ любых других уровней решетки) от уже существующего ЦМ 1-го уровня. Две разнонаправленные тенденции по размещению нового ЦМ – быть ближе (для минимизации транспортных издержек) и быть дальше (для формирования своего собственного “рынка”) по отношению к уже существующему – приводят к появлению ЦМ, расположенного в определенной степени посредине между двумя крайними вариантами.

Пожалуй, единственная аксиома, к которой мы не имеем претензий, – это третья. Отметим, что мы не считаем аксиомы неверными – они лишь должны быть уточнены для корректной дальнейшей работы.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

Начнем с первой аксиомы. В классической (кристаллеровской) ТЦМ численность населения зоны уровня n характеризуется (Parr, 1969) следующим уравнением (1):

где P_n – численность населения зоны уровня иерархии n; p_n – численность населения одного ЦМ уровня иерархии n; K – вариант кристаллеровской иерархии (в классической ТЦМ K = 3 или 4, или 7).

Представим, что все поселения некой системы центральных мест иерархичны по крайней мере в отношении численности их населения – на самом деле, в большинстве реальных случаев так оно и есть, поскольку иерархия свойственна не только городским, но и сельским поселениям, входящим в единую систему. Возьмем для дальнейшего рассмотрения все иерархичные поселения с номерами от 1 до некоего n (нумерация уровней производится сверху) и выпишем систему уравнений (2), описывающих численность населения каждой зоны соответствующего уровня, за исключением первой и последней. Вставим последовательно все уравнения системы (2), начиная с верхнего, в уравнение (1):

Произведя некоторые преобразования, получим уравнение (3), отражающее численность населения всей системы:

При этом сумма слагаемых в квадратных скобках представляет собой численность населения зон всех уровней иерархии с 1-го до (n – 1)-го. Два последних слагаемых вне скобок образуют численность населения зон уровня n (последнего, взятого нами для рассмотрения) и всех нижележащих иерархических уровней. “Очистим” последние от уровня n. Тогда (3) примет вид (4):

где сумма слагаемых в квадратных скобках представляет собой численность населения зон всех рассматриваемых уровней с 1-го до n-го, а далее (вне квадратных скобок) – численность населения зон всех нижележащих уровней.

Произведя преобразования “внескобочного” участка правой части (4), получаем, что суммарная численность населения всех зон уровней иерархии ниже n равна K^{n – 1} × (P_n – p_n). Тогда, используя уравнение Бекманна–Парра (Parr, 1969) и произведя некоторые преобразования, находим, что доля (ν) численности населения всех ЦМ уровней иерархии ниже n-го в населении всей рассматриваемой системы расселения выражается уравнением (5):

Тогда суммарная доля всех ЦМ с 1-го до n-го в населении всей рассматриваемой системы расселения выражается уравнением (6):

В данном случае k представляет собой долю центрального места в населении обслуживаемой им зоны. Как было показано В.А. Шупером (1995), значение k постоянно для всех уровней иерархии. Нам удалось установить существование нестрогого инварианта k в виде его максимального значения (Дмитриев, 2019а), равного K – $\sqrt {{{K}^{2}} - K} .$ Учитывая это, выявлено, что для любого n и при одном и том же значении K, равно как и для любого K при одном и том же значении n, график зависимости доли центральных мест всех уровней с 1-го до n-го в населении системы расселения (φ) от доли центрального места в населении обслуживаемой им зоны (k) носит характер непрерывной монотонно возрастающей функции, определенной на всем интервале значений k. Иными словами, доля численности населения центральных мест всех уровней с 1-го до n-го в населении всей системы расселения может быть любой – фактически от 0 до максимума при максимуме же k.

Среди всего многообразия случаев того, что мы считаем ЦМ уровней с 1-го до n-го, есть один очень важный – когда в качестве них мы будем рассматривать все городские населенные пункты. В этом случае, очевидно, φ представляет собой долю городского населения. В работах российского исследователя А.А. Важенина по ТЦМ была установлена зависимость типа кристаллеровской иерархии от уровня урбанизации. На ограниченном эмпирическом материале им было установлено, что система ЦМ эволюционирует по следующей схеме (табл. 1).

Учитывая приведенные выше доказательства, мы можем сказать, что выявленная А.А. Важениным закономерность – лишь частный случай из всего фактически неограниченного их числа. Таким образом, первый результат нашего исследования состоит в том, что на самом деле не существует выраженной зависимости между эволюцией системы ЦМ от K = 2 к K = 7 и изменением уровня урбанизации.

Может показаться, что предложенные нами расчеты справедливы лишь в том случае, если $n \ne {{n}_{{\max }}},$ т.е. присутствует хотя бы один уровень иерархии ниже n. Действительно, ведь k, т.е. доля ЦМ в населении обслуживаемой им зоны, постояннa для всех уровней иерархии. На самом деле в доказательстве постоянства k в классической ТЦМ при “выходе” на уравнение Бекманна–Парра говорится о соотношении уровней (смежных или не смежных), но ничего не говорится о постоянстве k именно для последнего уровня. Если представить, что за ним нет других уровней, то значение k для него отличается от соответствующего значения для всех остальных уровней и равно 1, а численность населения одной зоны данного уровня равна численности населения его ЦМ.

Иными словами, если мы говорим о фактической иерархии всех уровней в системе ЦМ (без или с разделением на городское и сельское или любое другое население), то без какого-либо ущерба для самой теории ТЦМ ее первая аксиома может быть изменена и формулироваться следующим образом: “пространство однородно и изотропно во всех отношениях, за исключением распределения всего населения или его части”. В этом смысле, несмотря на высказывавшиеся ранее замечания (Parr, Denike, 1970), можно утверждать, что существование систем ЦМ со 100-процентным уровнем урбанизации ни в коей мере не противоречит самой теории в ее классическом варианте.

В то же время уравнение, позволяющее определить долю ЦМ рассматриваемых уровней во всей системе, может дать нам гораздо больше. Речь здесь идет о таком важном и, пожалуй, – по словам критиков ТЦМ – наиболее уязвимом ее аспекте, как динамизм (вернее, его отсутствие) (Preston, 1983). Действительно, не ясно, как происходит появление новых ЦМ в системе (можно даже назвать этот процесс эволюцией) – т.е., в конечном счете, как происходит появление новых уровней иерархии (показатель n), и как эти уровни заполняются (показатель K). При фиксировании одного из этих параметров проблем не возникает, однако на самом деле K и n могут меняться – по крайней мере судя по виду уравнения (6) – почти независимо друг от друга. Но это лишь на первый взгляд: на самом деле процесс эволюции систем расселения в аспекте классической ТЦМ достаточно строг. На доказательстве этого утверждения мы бы и хотели остановиться далее.

Вероятно, для систем расселения в рамках ТЦМ действительно в процессе эволюции характерен (по крайней мере, до некоторого момента) рост численности городского населения (Эм, 2013). Это особенно важно для закрытых систем с иерархическими показателями роста численности населения всех уровней (в соответствии с их иерархией по численности населения) или для систем с постоянным населением: иными словами, новым ЦМ-городам в таких системах просто неоткуда взяться, кроме как из сельского населения. Для установления порядка эволюции систем ЦМ важно, чтобы изменения эти носили по возможности наиболее монотонный характер, т.е. в конечном итоге, чтобы график функции φ не имел разрывов первого и второго рода. Это означает, что в каждой точке – по крайней мере на интервале от 0 до 1 – мы можем найти его производную. Причем фактически это будут частные производные, поскольку это функция трех переменных (k, K, n). Формально мы можем зафиксировать одну или даже две из них и посмотреть, что происходит с функцией дальше, но тогда мы уйдем от главной задачи – выяснить, какова же картина при трех нефиксированных переменных.

Действительно, фиксировать K и n мы не имеем права, а вот с k дело обстоит не так однозначно. Построим графики функции φ = 1 – (1 – k) × × ${{\left( {\frac{{K(1 - k)}}{{K - k}}} \right)}^{{n - 1}}}$ при почти полярных значениях k, равных 0.1 и 0.5 – за эти пределы функция выходит редко (рис. 1).

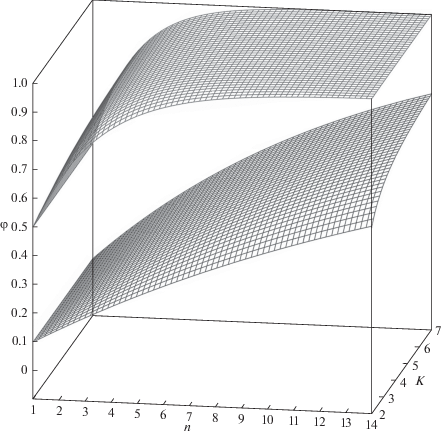
На первый взгляд, один из них не похож на другой, но не такие они и разные: в этом можно убедиться, если найти производную по направлению каждой из функций. Однако перед тем как сделать это, посмотрим на изменение числа ЦМ при изменении n и K в системе расселения. Учитывая, что нас интересует как можно более монотонное возрастание φ, при “нахождении” в том или ином прямоугольнике (табл. 2; на штриховку по периметру ячеек пока не обращаем внимания) движение возможно либо по горизонтали, либо по вертикали. Более того, длина его не превышает одного шага вправо или вниз. В противном случае φ будет расти не самыми медленными темпами или вообще убывать.

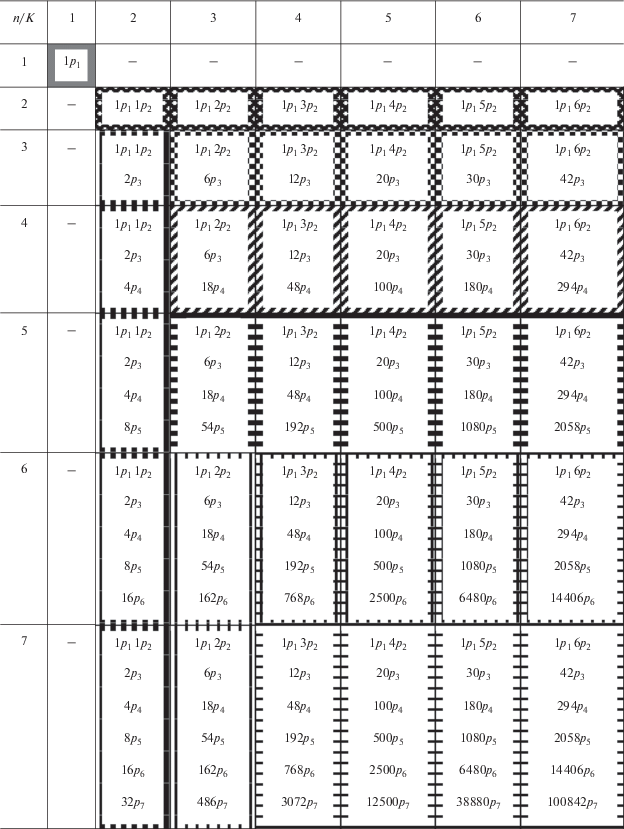
Представим, что система эволюционирует “с самого начала” и однонаправленно, т.е. движется от прямоугольника с координатами n и K соответственно (1; 1) к прямоугольнику (2; 2). Дальнейший путь не так очевиден, поскольку минимальное изменение системы ЦМ заключается в “переходе” в прямоугольник с координатами, одна из которых увеличивается на единицу по сравнению с (2; 2) – в (2; 3) или в (3; 2). Посмотрим, какой из них предпочтительнее.

Для этого, используя уравнение (7), найдем значения производной функции φ в точке (2; 2) по направлению (l_n; l_K) при k = 0.1 и k = 0.5:

где cos α = $\frac{{{{l}_{n}}}}{{\left| {\bar {l}} \right|}};$ cos β = $\frac{{{{l}_{K}}}}{{\left| {\bar {l}} \right|}}$ – направляющие косинусы;

Она представляет собой скорость изменения функции в заданном направлении. Она максимальна для точки (3; 2), однако в случае ее выбора в качестве следующего шага развития системы расселения будет наблюдаться больший рост φ, чем в случае точки (2; 3). Нас же интересует наименьшее приращение функции, поэтому далее на каждом шаге мы будем ориентироваться именно на наименьшее из полученных значений.

В дальнейшем весь алгоритм был пошагово повторен для каждого прямоугольника таблицы, причем для контроля брались также примыкающие по диагонали прямоугольники. Оказалось, что вне зависимости от значения k направление и длина шага от текущей ячейки – одни и те же. Таким образом, характер эволюции системы расселения в аспекте теории ЦМ зависит только от числа уровней иерархии в ней и их соподчиненности. Результат проиллюстрирован штриховкой по периметру ячеек в табл. 2.

Первый шаг (темная однотонная заливка по периметру значения в ячейке) – формирование одного ЦМ 1-го уровня. Далее появляется еще одно ЦМ – ячейка с координатами (2; 2). А вот далее эволюция системы расселения идет прежде всего “по строкам”, то есть основная тенденция – заполнение текущего уровня иерархии, прежде чем произойдет переход к следующему. Однако здесь есть два исключения: 1) после заполнения второго уровня иерархии появление двух первых ЦМ 3-го уровня (ячейка (3; 2)) приводит не к его дальнейшему заполнению, а к формированию системы расселения между одним ЦМ 1-го уровня и одним ЦМ 2-го уровня (движение вниз по столбцу для К = 2). После окончания этого процесса эволюция возвращается в свое нормальное русло: последовательно заполняются третий, четвертый и пятый уровни. После этого процесс снова прерывается в ячейке (6; 3) формированием подсистемы расселения (столбец для K = 3), чтобы затем снова вернуться к нормальному ходу.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Таким образом, эволюция системы расселения в рамках участка решетки Кристаллера от первого ЦМ до числа уровней, например равного 5, и K = 3, происходит следующим образом – рис. 2 (при этом аналогичные процессы протекают во всех зонах одного и того же уровня).

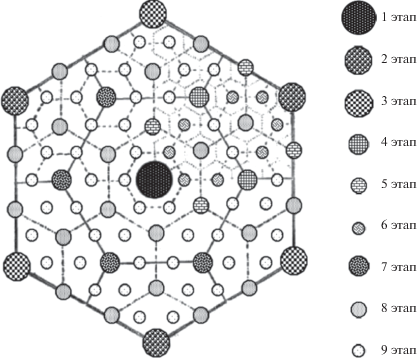
В классической ТЦМ K интерпретируется и как число ЦМ следующего уровня иерархии, обслуживаемое одним центральным местом данного уровня (плюс оно само), и как отношение квадратов расстояния между ЦМ одного уровня иерархии (например, третьего) и расстояния между ЦМ смежных уровней (например, третьего и четвертого). Во втором случае важно то, как мы считаем эти расстояния – на плоскости (как Кристаллер) или же используя другие координатные системы (например, сферическую). Подобные нововведения предлагались некоторыми специалистами, в том числе и в одной из наших работ (Дмитриев, 2019б). Более того, если мы переходим к объемным моделям систем ЦМ, то шестиугольниками замостить сферу уже не получится – нужно будет вводить определенное число пятиугольников. Это может существенно усложнить расчеты и привести к совсем иным результатам относительно эволюции систем ЦМ.

В то же время уравнение производной по направлению носит инвариантный характер, т.е. его вид справедлив для любых систем отсчета. Если говорить проще, то не имеет значения, представляют ли собой n и K обычные переменные или же сами, в свою очередь, являются функциями. Таким образом, процесс эволюции систем расселения происходит одинаково в любой системе координат; трансформация ТЦМ “от” декартовой системы к сферической (или любой другой) в этом отношении не требуется.

Однако вернемся к собственно эволюции. В работе А.А. Важенина (1997) было предложено рассматривать системы расселения как состоящие из изолированных подсистем, в которых сохраняются углы и расстояния между ЦМ смежных уровней, которые характерны для классической кристаллеровской решетки. Этот подход действительно очень заманчив, поскольку позволяет ограничить число центральных мест сверху, т.е. изолировать систему расселения, придав ей вид моноцентрической применительно к первому уровню иерархии. В этом случае появляется возможность анализировать изолированные системы расселения (например, островные) (Важенин, 2008).

В то же время этот подход, формально не противореча аксиоматической основе ТЦМ, вычеркивает из ее состава пятую составляющую, поскольку в этом случае не только ЦМ первого уровня может извлекать сверхприбыль, но и остальные. Причем этот процесс будет затрагивать всю систему расселения, так как одно ЦМ данного уровня, дабы компенсировать свои потери в пользу ЦМ предшествующего уровня, будет увеличивать доходы со своих ЦМ более низкого уровня. Поведение же потребителя остается “рациональным” вынужденно, поскольку никуда из ЦМ своего уровня за получением центральных услуг более высокого ранга он не может поехать, кроме как в одно ЦМ более высокого уровня. Таким образом, в случае рассмотрения систем расселения как систем ЦМ, формирующихся изолированно, пятая аксиома ТЦМ о “рациональном” поведении потребителя может считаться избыточной.

Это же происходит и со второй аксиомой, поскольку возможность изолированности (конечности) систем ЦМ сверху, установленную А.А. Важениным, нам в рамках настоящего исследования удалось дополнить возможностью изолированности (конечности) снизу. Таким образом, в случае рассмотрения систем расселения как систем ЦМ, формирующихся изолированно, вторая аксиома ТЦМ о бесконечности пространства отвергается.

ЗАКЛЮЧЕНИЕ

Таким образом, эволюция системы расселения в аспекте классической ТЦМ происходит преимущественно путем последовательного заполнения уровней иерархии, прерывающегося появлением подсистем расселения. При этом пока мы не можем дать однозначного ответа на вопросы о том, носит ли это прерывание периодический характер или же свойственно только каким-то отдельным шагам в формировании системы расселения, а также почему подсистемы появляются именно в данных точках бифуркации (в контексте процесса самоорганизации расселения) – для этого требуются дополнительные исследования.

При этом необходимо отметить, что “последовательное заполнение” совершенно не означает появления всех шести центральных мест, например, на втором уровне иерархии и лишь последующего заполнения третьего уровня. Заполнение – это и одно, и/или два, и/или три центральных места, с появлением которых процесс на втором уровне иерархии может закончиться и перейти к третьему уровню; а может и пойти дальше на том же втором уровне. Это действительно так: мы можем видеть это по рис. 2 (с K = 3) – на девятом этапе эволюции все уровни полностью заполнены, а K не равно семи. Таким образом, полнота заполнения заключается не в появлении всех потенциально возможных центральных мест на данном уровне, а лишь тех из них, появление которых возможно при данных параметрах системы центральных мест (в частности k).

Очевидно, что в процессе эволюции реальных систем расселения совершенно не обязательно появление сразу нескольких населенных пунктов, а если даже это и произошло, то не во всех зонах (Горохов, Дмитриев, 2009). В этом случае, очевидно, мы будем иметь систему с разными значениями K для разных уровней. В то же время, как удалось установить, такие состояния являются промежуточными – система стремится дозаполнить все уровни иерархии.

Вероятно, можно провести параллели между этапами эволюции систем ЦМ по Кристаллеру и типами территориальных структур расселения по Г.М. Лаппо (1978). Так, концентрический, полицентрический, частично бассейновый и центральный типы напоминают традиционную решетку. В то же время, вероятно, эволюция может первым своим шагом иметь и формирование подсистемы ЦМ (аналог линейного типа), и начинаться с ЦМ, расположенного на окраине (приморский тип).