Известия РАН. Серия географическая, 2021, T. 85, № 3, стр. 458-466

ВВЕДЕНИЕ

Определение общего понятия “интеграция” можно найти во многих словарях. Например, в (Толковый…, 1935) интеграция, как научный термин, описана следующим образом: “Объединение в целое каких-нибудь частей или элементов в процессе развития”.

В различных областях знания это понятие имеет свои особенности. В частности, интеграция пространственных данных связана с координатными описаниями объектов и их взаимным расположением. Но даже и в этой конкретной области существуют разные подходы. Инвентаризация ресурсов пространственных данных, распределенных, в рамках инфраструктур пространственных данных на основе метаданных рассмотрена в работе (Кошкарев и др., 2010).

При интеграции пространственных данных с целью генерации новых информационных продуктов эффективным инструментом получения единой картографической основы является разбиение поверхности относимости на ячейки регулярной сетки той или иной формы и размера. Описание такого способа представлено много лет назад (Koshkarev, 1979). Примером современного применения такого подхода может служить Единая европейская регулярная сетка CGRS – Common European Chorological Grid Reference System¹¹, использованная в сервисе “Млекопитающие России”²² (Сервис…, 2021).

Интеграцию пространственных данных для картографических целей целесообразно начинать с приведения разнородных данных к единой системе координат (Никифорова и др., 2014). При выборе системы координат, а в частности при выборе проекции создаваемой карты, можно задавать различные варианты. Однако при использовании существующей карты необходимо точно знать параметры системы координат, в которой она была составлена. Это важно для мелкомасштабных карт, так как проекции могут сильно отличаться. Кроме того, при включении карты в геоинформационную систему для согласования с данными других карт или для анализа тематической нагрузки необходимо, чтобы используемое программное обеспечение поддерживало проекцию карты.

Для изображения территории нашей страны в основном используются конические проекции в нормальной ориентировке, различные по распределению искажений. Особое место среди них занимает проекция Ф.Н. Красовского, который в 1920-х годах предложил способ получения равнопромежуточных конических проекций исходя из условия сохранения площади широтного пояса, ограниченного заданными параллелями (Гинзбург и др., 1955). В настоящее время под конической проекцией Красовского понимается один из вариантов такой проекции с выбранным широтным поясом, ограниченным параллелями 39°28′42″ и 73°28′42″ северной широты. Эта проекция представлена в Атласе для выбора картографических проекций под номером 11 (Гинзбург, Салманова, 1957). Широты секущих параллелей конуса, обычно используемые при описании проекций в ГИС-пакетах, равны в градусах 66.7251 и 50.6544. В проекции Красовского, первоначально разработанной для изображения европейской части СССР, создавались затем и карты всей территории СССР и России. Конические проекции, также как и азимутальные, используемые для изображения полярной области, поддерживаются практически всеми картографическими программными продуктами. Однако вся территория страны с учетом полярных владений может быть наилучшим образом показана в косых перспективно-цилиндрических проекциях. Именно поэтому такая проекция (проекция ЦНИИГАиК) была использована при создании Национального атласа России (Национальный …, 2004–2008). В (Гинзбург, Салманова, 1957) эта проекция представлена под номером 13.

Кроме того, другой вариант косой перспективно-цилиндрической проекции – проекция Соловьёва, номер 15 в (Гинзбург, Салманова, 1957) – использовался для школьных карт, так как она дает хорошее представление о шарообразности Земли. На школьные контурные карты некоторые ученые наносили результаты своей работы, что дает возможность включать эти результаты в процесс дальнейших исследований.

Данные о характере искажений вышеупомянутых проекций содержатся в Атласе для выбора картографических проекций (Гинзбург, Салманова, 1957).

Обеспечение поддержки популярными ГИС-пакетами косых перспективно-цилиндрических проекций расширит возможности использования данных с карт, составленных в этих проекциях.

ПЕРСПЕКТИВНО-ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ В НОРМАЛЬНОЙ ОРИЕНТИРОВКЕ

Перспективно-цилиндрические проекции являются проекциями в геометрическом смысле этого слова. Как правило, это проекции сферы. Перспективно-цилиндрические проекции в нормальной ориентировке используются при создании карт довольно давно и описаны как в отечественной, так и в зарубежной литературе (например, проекция Голла в (Snyder, Voxland, 1989)). На рис. 1 представлена плоскость меридианного сечения сферы радиуса R с точкой глаза O, из которой производится проектирование точек противоположного меридиана на противоположную же сторону секущего цилиндра. Здесь D – расстояние от точки глаза до центра окружности, ${{\Phi }_{k}}$ – широта (на сфере) параллели сечения. Слева (см. рис. 1а) – случай, когда D < ∞, справа (см. рис. 1б) – когда D = ∞.

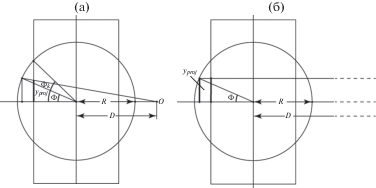
При проектировании точек других меридианов точка глаза описывает окружность радиуса D. Формулы пересчета из географических координат Φ, λ в прямоугольные ${{x}_{{proj}}},~{{y}_{{proj}}}$ для перспективно-цилиндрических проекций сферы в нормальной ориентировке можно найти во многих учебниках по математической картографии, например в последней книге М.Д. Соловьёва (1969). Но обратный пересчет из прямоугольных координат в географические не отражен и потребовался только в эпоху ГИС. В плоскости проекции мы используем прямоугольную систему координат, у которой координатная ось X_proj направлена горизонтально вправо, а координатная ось Y_proj направлена вертикально вверх (в отличие от принятой в отечественной литературе по геодезии и математической картографии).

Формулы для первого случая (см. рис. 1а):

где λ₀ – долгота меридиана, проходящего через начало координат в плоскости проекции, $K = \frac{D}{R}$ – отношение расстояния от точки глаза до центра сферы к радиусу сферы.

Для касательного цилиндра ${{\Phi }_{k}} = 0~\,\,{\text{и}}~$ $\cos {{\Phi }_{k}} = 1$.

Формулы для второго случая (см. рис. 1б):

Долгота при заданном значении$~{{x}_{{proj}}}$ получается из (1):

Широта при заданном значении ${{y}_{{proj}}}$ при $K < \infty $ получается из (2), при $K = \infty $ из (3).

При ${\text{\;}}~{{y}_{{proj}}} = 0$ широта также равна нулю $\left( {\Phi = 0} \right)$.

При ${\text{\;}}~{{y}_{{proj}}} \ne 0\,\,~{\text{и}}~\,\,K < \infty $ (см. (2)) получение обратной формулы сводится к решению квадратного уравнения относительно $\sin \Phi $:

При ${\text{\;}}~{{y}_{{proj}}} > 0$ выбирается знак плюс, при ${\text{\;}}~{{y}_{{proj}}} < 0$ выбирается знак минус.

Окончательные формулы пересчета из прямоугольных координат в географические для перспективно-цилиндрических проекций сферы в нормальной ориентировке, выведенные в рамках данной работы:

При $K < \infty $ используется (5), при $K = \infty $ используется (6).

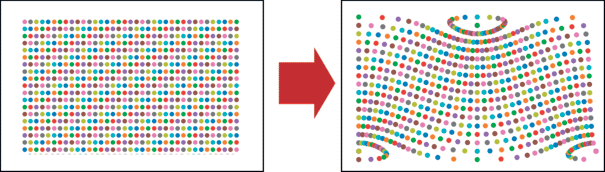
На рис. 2 представлен пересчет географических координат (долгота/широта) в проекцию Голла. Слева показаны узлы картографической сетки, причем по горизонтальной оси отложена долгота, а по вертикальной оси – широта. Справа – эти узлы в перспективно-цилиндрической проекции Голла. Параметры проекции Голла по (Snyder, Voxland, 1989): ${{\Phi }_{k}} = 45^\circ ,~K = 1$.

Отметим, что такое отображение на плоскости долготы/широты соответствует цилиндрической равнопромежуточной по меридианам проекции для касательного цилиндра в нормальной ориентировке. Другое название этой проекции “квадратная”, или “проекция Plate Carrée”.

КОСЫЕ ПЕРСПЕКТИВНО-ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ

Косые перспективно-цилиндрические проекции были получены в нашей стране в 30-е годы XX в., но не вошли в труды американского картографа Дж. Снайдера и, как следствие, в зарубежные геоинформационные программные продукты. Отечественные картографические пакеты “Нева”, разработанный в Институте проблем управления РАН, и ГеоГраф, разработанный в Институте географии РАН, поддерживают эти проекции. Однако списки картографических проекций таких популярных программных продуктов, как ArcGIS и QGIS, не содержат косых перспективно-цилиндрических проекций для эллипсоида вращения.

Наиболее эффективным способом адаптации перспективно-цилиндрических проекций для включения в популярные ГИС-пакеты является их реализация в библиотеке PROJ³³. Эта библиотека используется разработчиками многих программных продуктов для преобразования картографических проекций и геодезических систем координат. Для включения картографической проекции в библиотеку PROJ, необходимо дать ее полное описание. Для использования проекции в ГИС-пакетах требуется в дальнейшем получение уникального кода проекции в реестре идентификаторов картографических проекций EPSG. Описание проекции включает в себя формулы пересчета из географических координат в прямоугольные и из прямоугольных в географические в текстовом виде и в виде компьютерной программы.

Пересчет географических координат на сфере в косую перспективно-цилиндрическую проекцию проводится в два этапа. Сначала осуществляется переход к географическим координатам в косой ориентировке ${{\Phi }_{{obl}}},~{{\lambda }_{{obl}}}$ и затем пересчет в координаты проекции по формулам для нормальной ориентировки. На рис. 3 показано положение сферы относительно секущего цилиндра в нормальной (см. рис. 3а) и косой (см. рис. 3б, 3в) ориентировке. На рис. 3б – взгляд со стороны меридиана $~{{\lambda }_{{obl}}} = 180^\circ $, а на рис. 3в – взгляд со стороны меридиана $~{{\lambda }_{{obl}}} = 0^\circ $. Обычно при описании геометрии цилиндрической проекции в косой ориентировке меняют положение цилиндра. Однако поворот сферы относительно неподвижного цилиндра бо-лее наглядно иллюстрирует переход к географическим координатам в косой ориентировке. Географический полюс на рисунке обозначен буквой P, а полюс косой системы координат обозначен ${{P}_{{obl}}}$. В нормальной ориентировке координаты ${{P}_{{obl}}}$ равны ${{\Phi }_{0}},~{{\lambda }_{0}}$. Координаты точки A в нормальной ориентировке равны $\Phi ,~\lambda $, а при повороте сферы становятся ${{\Phi }_{{obl}}},~{{\lambda }_{{obl}}}$.

Формулы перехода от географических координат в нормальной ориентировке к косой ориентировке есть во многих работах по математической картографии. Как правило, переход осуществляется через полярные сферические координаты (зенитное расстояние и азимут) с использованием сферического треугольника. Например, из формул, представленных в справочной таблице в (Гинзбург и др., 1955), можно получить следующие формулы:

Если ${{\Phi }_{{obl}}} = \pm 90^\circ $, принимаем ${{\lambda }_{{obl}}} = 0$.

При программировании целесообразно использовать функцию atan2:

Это позволяет учесть знаки синуса и косинуса и избежать деления на ноль.

Если не использовать функцию atan2, случай $\Phi = \pm 90^\circ $ надо рассмотреть отдельно. Если $\Phi = 90^\circ $, то ${{\Phi }_{{obl}}} = {{\Phi }_{0}},~\,\,\lambda = 0$. Если $\Phi = - 90^\circ $, то ${{\Phi }_{{obl}}} = - {{\Phi }_{0}},\,\,~{{\lambda }_{{obl}}} = 180^\circ $.

Те же самые формулы можно использовать и для обратного преобразования с учетом того, что в системе координат, соответствующей косой ориентировке, долгота и широта географического полюса, соответствующего нормальной ориентировке, равны нулю и ${{\Phi }_{0}}$ соответственно (см. рис. 3). Подставляя в (10) и (11) ${{\Phi }_{{obl}}}$ вместо $\Phi $, ${{\lambda }_{{obl}}}$ вместо $\lambda - {{\lambda }_{0}}$, $\Phi $ вместо ${{\Phi }_{{obl}}}$ и $\lambda - {{\lambda }_{0}}$ вместо ${{\lambda }_{{obl}}}$, получаем:

или

Такие же формулы можно получить непосредственно из (7), (8), (9).

Если $\Phi = \pm 90^\circ $, долготу определить невозможно и приходится принимать, например, $\lambda = {{\lambda }_{0}}$.

Если не использовать функцию atan2, случай ${{\Phi }_{{obl}}} = \pm 90^\circ $ надо рассмотреть отдельно, также как это было сделано для $\Phi = \pm 90^\circ $. Если ${{\Phi }_{{obl}}} = 90^\circ $ , то $\Phi = {{\Phi }_{0}},\,\,~\lambda = {{\lambda }_{0}}$. Если ${{\Phi }_{{obl}}} = - 90^\circ $, то $\Phi = - {{\Phi }_{0}},~$ $\lambda = {{\lambda }_{0}} + 180$. Если долгота получится больше 360$^\circ $, то надо отнять 360°.

На рис. 4 представлены слева узлы картографической сетки (долгота/широта) в нормальной ориентировке, а справа – в косой ориентировке. Широта полюса проекции ${{\Phi }_{0}} = 45^\circ $.

Отображение на плоскости долготы/широты в косой ориентировке (см. рис. 4б) дает нам цилиндрическую проекцию (касательный цилиндр), сохраняющую длины вдоль меридианов в косой ориентировке.

Перспективно-цилиндрические проекции сферы были разработаны для карт мелкого масштаба, и переход от поверхности эллипсоида вращения к сфере не имел существенного значения. Однако мелкомасштабная обзорная карта в составе мультимасштабной ГИС может быть основой для привязки карт более крупного масштаба. В этом случае необходим выбор геодезической системы координат, привязанной к эллипсоиду вращения. Кроме того, для работы с большинством ГИС-пакетов требуется выбрать геодезическую систему координат. Предлагается переход от поверхности эллипсоида к сфере под условием равновеликого отображения, так как этому соответствует радиус сферы, выбранный для реализации перспективно-цилиндрических проекций в (Гинзбург, Салманова, 1957). После некоторых преобразований формулы из (Snyder, 1987) приобретают вид:

где $a$ – большая полуось эллипсоида вращения, $b$ – малая полуось эллипсоида вращения, $\Phi $ – широта на сфере, $\varphi $ – геодезическая широта на эллипсоиде вращения, $e$ – эксцентриситет эллипса меридианного сечения, ${{R}_{q}}$ – радиус сферы, площадь поверхности которой равна площади поверхности эллипсоида.

Обратные формулы:

Таким образом пересчет геодезических координат, заданных на поверхности эллипсоида вращения, включает в себя три этапа:

1. Переход от поверхности эллипсоида к сфере под условием равновеликого отображения (см. (15)).

2. Переход от географических координат в нормальной ориентировке к косой ориентировке (см. (10), (11)).

3. Пересчет из географических координат в прямоугольные для перспективно-цилиндрических проекций сферы в нормальной ориентировке (см. (1), (2), (3)).

Частный масштаб площадей в косой перспективно-цилиндрической проекции эллипсоида вращения вычисляется аналогично. Первые два этапа такие же, как и при вычислении прямоугольных координат, а на третьем этапе вместо (1), (2), (3) используется формула вычисления частного масштаба площадей p для сферы в нормальной ориентировке (Соловьёв, 1969):

Это возможно, так как при переходе от поверхности эллипсоида к сфере площади сохраняются.

Пересчет из прямоугольных координат в географические также включает в себя три этапа, но расположенные в обратном порядке:

1. Пересчет из прямоугольных координат в географические для перспективно-цилиндрических проекций сферы в нормальной ориентировке (см. (4), (5), (6)).

2. Переход от географических координат в косой ориентировке к нормальной ориентировке (см. (13), (14)).

3. Переход от сферы к поверхности эллипсоида под условием равновеликого отображения (см. (16)).

Формулы пересчета запрограммированы на языке Phyton. Координаты точек для рис. 2 и 4 вычислены с помощью полученных программ. Таким образом, составлено полное описание косой перспективно-цилиндрической проекции для ее включения в библиотеку PROJ.

СОВРЕМЕННОЕ ПРИМЕНЕНИЕ ПЕРСПЕКТИВНО-ЦИЛИНДРИЧЕСКИХ ПРОЕКЦИЙ

Приведем примеры карт из Национального атласа России, составленные в перспективно-цилиндрической проекции ЦНИИГАиК. В первом томе: Физическая карта России, Федеративное устройство России, Земельные угодья, Федеральные округа, Часовые пояса, Плотность населения. Во втором томе: Геологическая карта, Аномалии магнитного поля, Аномалии гравитационного поля, Геоморфология. Морфоструктура, Леса, Современные рельефообразующие процессы.

Косые перспективно-цилиндрические проекции были также использованы при составлении карт Национального атласа Арктики (Национальный…, 2017).

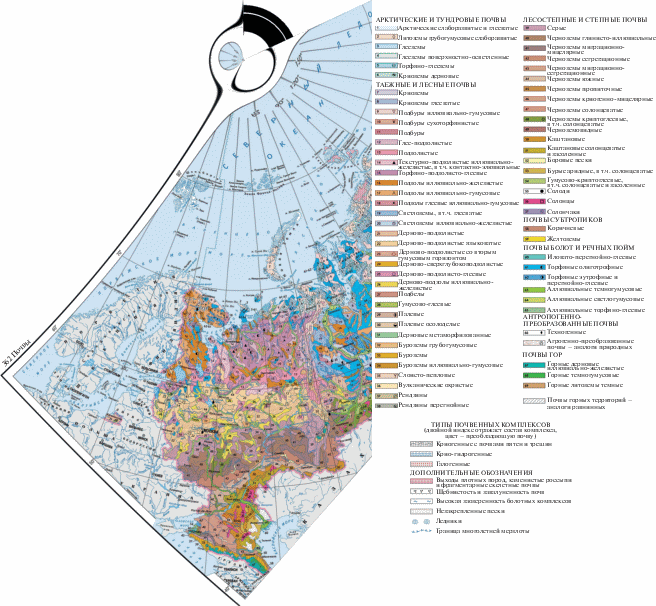
При создании некоторых карт Национального атласа России в перспективно-цилиндрической проекции ЦНИИГАиК $K = 3,~$ ${{\Phi }_{k}} = 10^\circ ,~$ ${{\Phi }_{0}} = 25^\circ ,~$ ${{\lambda }_{0}} = - 80^\circ $ были использованы карты, составленные ранее в других проекциях. Для корректной интеграции данных было произведено трансформирование отсканированных изображений карт-источников в проекцию ЦНИИГАиК. В том случае, когда для интеграции данных выбрана другая картографическая проекция, например коническая, и среди карт-источников есть карты из Национального атласа России, необходимо трансформировать эти карты в выбранную коническую проекцию. На рис. 5 представлен фрагмент отсканированного изображения почвенной карты России (Национальный…, 2004–2008, т. 1, с. 362), трансформированной из косой перспективно-цилиндрической проекции ЦНИИГАиК, в которой карта была составлена, в коническую проекцию Красовского.

Приведем пример использования косой перспективно-цилиндрической проекции Соловьёва, разработанной для школьных карт. Параметры этой проекции:

В книге (Соколов и др., 1977) ареалы распространения различных видов деревьев представлены в проекции Соловьёва. На рис. 6 показана карта ареала Populus tremula L (карта 65), пересчитанная из этой проекции в географические координаты долгота/широта.

В такой проекции карта может быть использована для анализа данных в любом ГИС-пакете. Трансформирование растровых изображений осуществлялось в программном продукте ГеоГраф ГИС 2.0.

ЗАКЛЮЧЕНИЕ

В нашей стране накоплен ценный фонд карт в косых перспективно-цилиндрических проекциях. Они могут быть использованы в научных исследованиях с применением инструментария ГИС. После включения этих проекций в библиотеку PROJ и получении кода EPSG операции по привязке и трансформированию для согласования и анализа с последующей интеграцией можно будет проводить во многих популярных ГИС-пакетах как в России, так и во всем мире.