Химическая физика, 2019, T. 38, № 5, стр. 10-16

ВВЕДЕНИЕ

Результаты теоретического и экспериментального изучения возбуждения вещества светом, содержащим когерентную совокупность двух монохроматических волн с разными частотами, отражены во многих работах, ссылки на которые приведены, например, в обзорах [1, 2] и монографиях [3, 4]. В этих работах дано объяснение происхождения и предложено практическое использование таких эффектов преобразования веществом бихроматического поля, как когерентное пленение населенностей состояний вещества, когерентный фотогальванический эффект, отличие спектральных характеристик вторичного излучения от известных характеристик при облучении монохроматическим светом (“триплет Моллоу”), увеличение интенсивности резонансной флуоресценции при таком возбуждении вещества, когда средняя частота компонент облучения равна субгармоникам частоты Раби, и др. В ряде работ предложено использовать бихроматическое облучение как метод управления фотопревращениями вещества путем изменения относительной фазы монохроматических компонент облучения. Список из 46 наименований работ по теоретическому изучению и практическому применению такого метода управления приведен в [4].

Заметим, что в тех работах по изучению динамики возбуждения двухуровневой частицы бихроматическим полем, которые приведены в [1–4], расчеты проводились с применением классического описания электромагнитного поля, хотя использовалась терминология квантовой теории поля излучения: однофотонное, двухфотонное и так далее поглощение облучения. Так в этих работах называлось поглощение при переходах частицы из основного в возбужденное состояние под действием соответственно компоненты бихроматического поля с частотой, равной “основной” частоте, компоненты с частотой, в два раза большей основной частоты, и т.д. Среди таких работ отметим работы [5, 6], в которых приводятся выражения в аналитическом виде для зависимости от времени заселенности возбужденного состояния частицы. Эти выражения получены на основе решения уравнения Шредингера для амплитуд заселенности состояний частицы как замкнутой квантовой системы во внешнем, описываемом классической теорией электромагнитном поле при использовании того или иного приближения и принятии ряда упрощающих расчеты допущений. Представляет интерес получить соответствующие выражения при использовании более последовательного и полного квантового представления о взаимодействии света с частицей в составной (общей) системе из частицы и квантованного поля излучения [7] и сравнить их с соответствующими выражениями отмеченных полуклассических расчетов, а также с данными экспериментального изучения динамики возбуждения двухуровневой частицы бихроматическим полем, такими, например, которые получены в работе [8] при определении заселенности состояния ³P₁ атома Yb, возбуждаемого бихроматическим полем.

Отметим, что аналитические зависимости от времени заселенности возбужденного состояния двухуровневой частицы при возбуждении монохроматическим светом, полученные на основе использования квантовой теории составной системы (КТСС) для случая строго резонансного облучения в монографии [9] и для случая облучения вблизи резонанса в монографии [10], существенно отличаются от зависимостей, полученных на основе формализма полуклассической теории оптических уравнений Блоха (ОУБ). Анализ причин и результатов такого различия позволяет, например, более обоснованно выбрать ту или иную точку зрения относительно интерпретации механизма фотопревращения вещества как процесса преобразования одного из фотонов облучения, согласно формализму КТСС, или как процесса преобразования многих фотонов облучения, согласно формализму ОУБ (см., например, [10]). Анализ сходства или различия результатов моделирования динамики возбуждения двухуровневой частицы при бихроматическом облучении на основе формализма КТСС или формализма ОУБ можно использовать для получения более полного представления о механизме происхождения перечисленных выше эффектов возбуждения вещества светом, содержащим когерентную совокупность двух монохроматических волн, и рассматривать как вклад в развитие теоретических основ отмеченного выше метода управления фотопревращениями вещества посредством выбора относительной начальной фазы монохроматических компонент облучения. Другим аспектом использования результатов анализа упомянутого сходства или различия является развитие представления о разнице в подходах к моделированию динамики возбуждения частицы импульсами разного вида, поскольку возбуждение частицы бихроматическим полем с частотами компонент, близкими к частоте ее собственного перехода в возбужденное состояние, можно рассматривать как простейший пример возбуждения частицы последовательностью импульсов облучения (см., например, приложение E6 в [1]).

Установление зависимости изменения характера динамики резонансно-возбуждаемого состояния молекулы от выбора тех значений параметров импульса облучения, при которых рассматривается дальнейший переход ее в желательное конечное состояние с минимальной потерей энергии и времени лежит в основе формализма теории одного из вариантов “оптимального квантового управления” ходом различных фотопревращений молекул (см. обзор [11] со списком литературы в 771 наименований). Успехи теории и практики такого управления (“контроля”), достигнутые к 2015 г., отражены в отчете “Общеевропейской комиссии по координации и поддержке работ по оптимальному квантовому управлению” (QUAINT) [12]. Этот отчет отражает мнение 144 экспертов при ссылках на 486 работ разных авторов в различных группах исследователей. Наряду с успехами в отчете отмечается потребность в совершенствовании применяемого формализма посредством учета достижений современной теории взаимодействия частицы со световым полем. Как отмечено выше, одним из направлений такого совершенствования обычно используемого формализма оптимального квантового управления можно считать переход от использования полуклассического представлении о взаимодействии импульса облучения с частицей (обычно применяемого в теории оптимального квантового управления на основе формализма ОУБ) к применению формализма КТСС. Данные анализа результатов моделирования динамики возбуждения двухуровневой частицы последовательностью импульсов, образуемых бихроматическим облучением, на основе применения этих двух методов можно использовать как исходный материал для работы по продвижению в отмеченном направлении совершенствования формализма оптимального квантового управления. В настоящей работе проведен такой анализ на одном из простейших примеров моделирования динамики заселенности состояний двухуровневой частицы: облучение последовательностью импульсов “синусоидальной” формы, образуемых сфазированным бихроматическим полем, частоты монохроматических компонент которого мало отличаются от собственной частоты перехода частицы, при строгом резонансе средней частоты облучения с собственной частотой частицы и условии, что радиационное время жизни возбужденного состояния частицы много больше периода колебания интенсивности принятого бихроматического облучения. Имея в виду выполнение такого условия, можно пренебрегать рассеянием фотонов облучения в любую из мод поля излучения в вакуумном состоянии, ограничиваясь учетом взаимодействия частицы только с полем двухмодового облучения. При использования таких допущений в настоящей работе получены выражения для зависимости от времени заселенности состояний частицы, которые сравниваются с соответствующими зависимостями, определяемыми численным решением системы оптических уравнений Блоха.

МОДЕЛЬ СОСТАВНОЙ СИСТЕМЫ

Место расположения частицы будем соотносить с центром декартовой системы координат $(X,Y,Z).$ При классическом описании поля излучения полагаем, что вектор поляризации электромагнитного поля облучения направлен по оси $X$ и параллелен вектору дипольного момента частицы. Напряженность поля облучения в центре системы координат запишем в виде

Соответствующее выражение для интенсивности облучения частицы (плотности потока энергии, усредненной по “быстрому” времени $t \approx \omega _{L}^{{ - 1}}$) имеет вид

Основное собственное состояние двухуровневой модели частицы будем отмечать индексом “1”, а возбужденное собственное состояние – индексом “2”. Энергии этих состояний обозначим через ${{E}_{1}}$ и ${{E}_{2}}$ $\left( {{{E}_{2}} - {{E}_{1}} \equiv \hbar {{\omega }_{{21}}}} \right).$ Ограничимся рассмотрением облучения с частотой ${{\omega }_{L}} = {{\omega }_{{21}}}.$ Матричный элемент оператора взаимодействия поля облучения и частицы по состояниям 1 и 2 в дипольном приближении имеет вид ${{V}_{{12}}} = - {{(e{{d}_{x}})}_{{12}}},$ где ${{d}_{x}} - $ проекция вектора дипольного момента частицы на ось $X;$ ${{({{d}_{x}})}_{{12}}} \equiv e_{0}^{{ - 1}}\hbar {{\Omega }_{R}},$ ${{\Omega }_{R}} - $ частота Раби. Для простоты записи опущено указание на зависимость от времени функции $e(t)$ и, соответственно, $V(t).$

При квантовом описании поля излучения ограничимся, как отмечено выше, рассмотрением поглощения одного из фотонов бихроматического поля, каждый из $N \gg 1$ фотонов которого находится в суперпозиционном состоянии

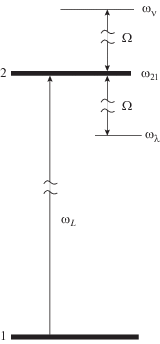
где $\left| {{{\phi }_{{\lambda }}}} \right\rangle $$\left( {\left| {{{\phi }_{\nu }}} \right\rangle } \right)$ – однофотонное состояние; $\lambda {\kern 1pt} \,(\nu )\,\; - $ набор квантовых чисел, характеризующих направление распространения и состояние поляризации фотона “сорта” $\lambda (\nu ).$ Будем полагать, что векторы поляризации фотонов $\lambda {\kern 1pt} $ и $\nu $ параллельны; ${{\omega }_{{21}}} - \Omega = {{\omega }_{\lambda }}$ – частота фотона $\lambda ;$ ${{\omega }_{{21}}} + \Omega = {{\omega }_{\nu }}$ – частота фотона сорта $\nu .$ Рисунок 1 схематично иллюстрирует соотношение между численными значениями частот ${{\omega }_{L}} = {{\omega }_{{21}}},$ ${{\omega }_{{\lambda }}},$ ${{\omega }_{\nu }}$ и $\Omega .$

Рис. 1.

Соотношения численных значений частоты компонент облучения и собственной частоты радиационного перехода частицы.

Квантовое среднее значение плотности потока энергии поля в рассматриваемом состоянии $\left| \phi \right\rangle $ (см. [13]) в центре куба периодичности ${{L}^{3}}$ имеет вид

Учитываемые состояния составной системы обозначены индексами “λ1”, “ν1”, “02”. Состояние $\lambda 1$ означает, что частица находится в состоянии 1, поле облучения содержит $N$ фотонов сорта $\lambda ;$ состояние $\nu 1$ означает, что частица находится в состоянии 1, поле облучения содержит $N$ фотонов сорта $\nu ;$ состояние $02$ означает, что частица находится в состоянии 2, а поле содержит $N - $ 1 фотонов.

Матричный элемент оператора V по состояниям $\lambda 1$ и $02$ записываем в виде

где ${{d}_{{\lambda }}}$ – проекция оператора дипольного момента частицы на направление поляризации фотона $\lambda .$ Аналогично выглядит выражение для матричного элемента оператора V по состояниям $\nu 1$ и $02.$ Как и ранее, полагаем, что вектор поляризации фотонов $\lambda $ и $\nu $ направлен по оси $X$ и параллелен вектору дипольного момента частицы, т.е. ${{d}_{{\lambda }}} = {{d}_{{\nu }}} = {{d}_{x}}.$ При сопоставлении результатов моделирования на основе формализма ОУБ с результатами моделирования, проведенного на основе формализма КТСС, будем полагать, что ${{\bar {\Omega }}_{R}} = {{\Omega }_{R}}.$

ИСПОЛЬЗОВАНИЕ ТЕОРИИ СОСТАВНОЙ СИСТЕМЫ

Уравнение Шредингера для амплитуды вероятности ${{b}_{k}}(t)$ заселенности собственного состояния $k$ составной системы в представлении взаимодействия запишем в виде

где $i,j,k$– индексы собственных состояний составной системы с энергиями ${{E}_{i}},$ ${{E}_{j}},$ ${{E}_{k}};$ $i - $ одно из начальных собственных состояний системы ($\lambda 1$ или $\nu 1$); ${{\omega }_{{ki}}} = {{\hbar }^{{ - 1}}}({{E}_{k}} - {{E}_{i}});$ ${{\delta }_{{ki}}}$ – символ Кронекера: ${{\delta }_{{ki}}} = 0$ при $k \ne i$ и ${{\delta }_{{ki}}} = 1$ при $k = i;$ $t - $ время; $\delta (t) - $ функция Дирака.

Фурье-представление функции ${{b}_{k}}(t)$ запишем в виде

где $E$ – энергетическая переменная.

Система уравнений для функций ${{G}_{{ki}}}(E)$ в резонансном приближении (см. [9]) записывается (для простоты записи опускаем индекс начального состояния) в виде

Решением этой системы уравнений являются следующие функции:

где $x \equiv {{\hbar }^{{ - 1}}}(E - {{E}_{{{\lambda 1}}}}),$ $F(x) = \hbar \sqrt 2 (x - \Omega ) \times $ $ \times \,\,\left[ {x(x - 2\Omega ) - 2\Omega _{R}^{2}} \right].$

При переходе к комплексному представлению $z \equiv x + i\varepsilon $ функция $F(z)$ имеет три полюса первого порядка:

где $\tilde {\Omega } \equiv {{\left( {{{\Omega }^{2}} + 2\Omega _{R}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$

Используя полученные функции ${{G}_{{\lambda 1}}}(z),$ ${{G}_{{02}}}(z),$ ${{G}_{{{\nu 1}}}}(z)$ и применяя правила контурного интегрирования, находим соответствующие выражения для амплитуд заселенности состояний составной системы соответствующего уравнения Шредингера, которые имеют следующий вид:

Зависимость от времени возбужденного состояния частицы при регистрации состояния поля излучения, соответствующего отсутствию одного из фотонов облучения, определяется функцией

а зависимость от времени заселенности начального состояния частицы определяется следующим выражением:

Приведенные выражения для заселенности состояний частицы существенно отличаются от соответствующих выражений из работ [5, 6], полученных на основе решения уравнения Шредингера для двухуровневой частицы разными методами с применением обобщенного резонансного (“лестничного”) приближения при принятых выше допущениях относительно параметров классически описываемого поля облучения и пренебрежении рассеянием фотона в моды свободного поля излучения. Заметим также, что в результате проведения вычислений, аналогичных тем, которые приведены выше, определена зависимость от времени заселенности состояний рассматриваемой составной системы при спонтанном излучении фотона в квантованное двухмодовое поле излучения в вакуумном состоянии при переходе частицы из возбужденного в момент $t = 0$ состояния в основное. Полученные при этом выражения для амплитуд и заселенности состояний частицы совпадают с соответствующими выражениями, которые получены в работе [14].

Проведены также аналогичные вычисления заселенности состояний рассматриваемой составной системы при облучении частицы в основном состоянии бихроматическим полем с другими соотношениями заселенности начальных состояний монохроматических компонент. Мы ограничились рассмотрением приведенного выбора равных начальных заселенностей этих компонент как наиболее простого и наглядного при решении поставленной задачи: сравнение вида определенных “импульсов заселенности” возбужденного состояния частицы с зависимостью от времени диагонального матричного элемента статистического оператора (матрицы плотности) для возбужденного состояния частицы.

Как следует из сравнения приведенных выше функций ${{I}_{0}}(t)$ и ${{P}_{{02}}}(t),$ зависимость от времени заселенности возбужденного состояния частицы отличается от зависимости от времени интенсивности облучения в месте расположения частицы. Различие этих зависимостей определяется тем, что частота $\tilde {\Omega }$ отличается от частоты $\Omega ,$ так что в зависимости от условия облучения, характеризуемого отношением $\alpha = {{{{\Omega }_{R}}} \mathord{\left/ {\vphantom {{{{\Omega }_{R}}} \Omega }} \right. \kern-0em} \Omega },$ частота осцилляций функции ${{P}_{{02}}}(t)$ меньше частоты осцилляций функции ${{I}_{0}}(t)$ при ${{\Omega }_{R}} < \Omega $ (в предельном случае ${{\Omega }_{R}} \ll \Omega $ – в два раза меньше), и больше – при ${{\Omega }_{R}} > \Omega .$

ИСПОЛЬЗОВАНИЕ ОПТИЧЕСКИХ УРАВНЕНИЙ БЛОХА

Систему ОУБ для элементов матрицы плотности ${{\rho }_{{nm}}}(t)$ рассматриваемой частицы как замкнутой квантовой системы, возмущаемой внешним полем $e(t),$ запишем в виде

Здесь для простоты записи опущено указание на зависимость элементов ${{\rho }_{{nm}}} = {{b}_{n}}b_{m}^{ * }$ от времени; $n,m$ и $l$ нумеруют состояния частицы, принимая значения 1 или 2; V = –e(t)d_x – оператор энергии взаимодействия частицы с полем; ${{b}_{n}}$ и ${{b}_{m}}$ – амплитуды вероятности заселенности состояний $n$ и $m$.

Пренебрегая в этих уравнениях слагаемыми, которые содержат множители, осциллирующие соответственно с частотами $2{{\omega }_{{21}}} + \Omega $ и $2{{\omega }_{{21}}} - \Omega ,$ по сравнению со слагаемыми, осциллирующими с частотой $\Omega ,$ имеем систему ОУБ в приближении вращающейся волны:

Такое приближение соответствует резонансному приближению, использованному при решении уравнения Шредингера для составной системы.

СРАВНЕНИЕ ДИНАМИКИ ВОЗБУЖДЕНИЯ ЧАСТИЦЫ, ОПРЕДЕЛЕННОЙ ДВУМЯ МЕТОДАМИ

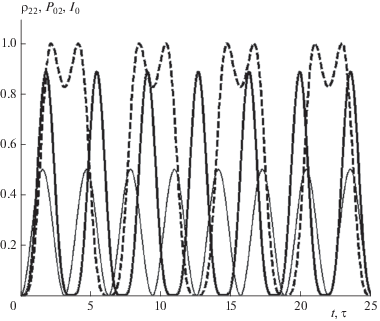
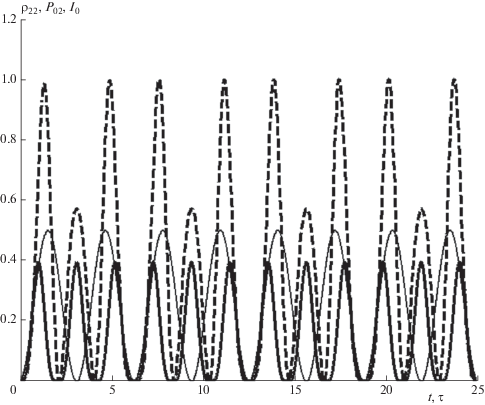
Сравнение вида полученных зависимостей ${{P}_{{02}}}(t),$ определяющих динамику возбуждения частицы на основе формализма КТСС, с видом соответствующих зависимостей $\,{{\rho }_{{22}}}(t),$ полученных в результате численных решений системы уравнений Блоха, отражено на рис. 2–4 для трех случаев облучения, характеризуемых различными значениями $\alpha .$ На этих рисунках функции ${{P}_{{02}}}(t)$ изображены утолщенными сплошными кривыми, а функции $\,{{\rho }_{{22}}}(t)$ – штриховыми кривыми; тонкими сплошными кривыми изображены соответствующие функции ${{I}_{0}}(t),$ отложенные в единицах $0.25\,cN{{L}^{{ - 3}}}\hbar {{\omega }_{{21}}};$ по оси абсцисс отложено безразмерное “время” $\tau = \Omega t.$

Рис. 2.

Динамика возбуждения частицы, определенная на основе формализма КТСС и формализма ОУБ при облучении частицы, характеризуемом отношением $\alpha = 0.1$ (пояснение см. в тексте).

Рис. 3.

То же, что и на рис. 2, для случая $\alpha = 1.$

Рис. 4.

То же, что и на рис. 2, для случая $\alpha = 2.$

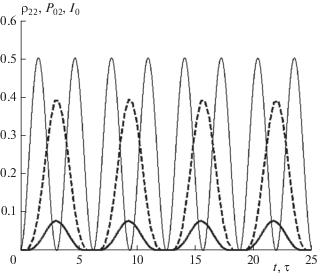
Приведенные на рис. 2 зависимости $\,{{\rho }_{{22}}}(t),$ ${{P}_{{02}}}(t)$ и ${{I}_{0}}(t)$ соответствуют случаю облучения, характеризуемому отношением $\alpha = 0.1.$ Зависимости $\,{{\rho }_{{22}}}(t)$ и ${{P}_{{02}}}(t)$ при этом выглядят как четыре “импульса заселенности” возбужденного состояния частицы с максимумами соответственно при $\,{{\rho }_{{22}}} \approx 0.4,$ ${{P}_{{02}}} \approx 0.06.$ Каждый из этих импульсов появляется в ответ на два импульса облучения ${{I}_{0}}(t),$ что качественно согласуется с результатами работ [15, 16]. В работе [15] проведено моделирование динамики возбуждения классически описываемым бихроматическим облучением классического осциллятора и двухуровневой частицы, а в работе [16] – моделирование динамики возбуждения двухуровневой частицы бихроматическим облучением проведено гамильтоновским методом в рамках классической электродинамики.

Рисунок 3 иллюстрирует различие формы импульсов ${{P}_{{02}}}(t)$ и $\,{{\rho }_{{22}}}(t)$ в случае облучения частицы, характеризуемом отношением $\alpha = 1.$ При таком облучении каждый импульс ${{P}_{{02}}}(t)$ несколько отстает от соответствующего импульса ${{I}_{0}}(t)$ (так что за время $25\,\tau $ вместо восьми импульсов облучения имеем семь импульсов заселенности частицы с максимумами при ${{P}_{{02}}} = {8 \mathord{\left/ {\vphantom {8 9}} \right. \kern-0em} 9}$), а каждый импульс $\,{{\rho }_{{22}}}(t)$ появляется во время спада функции ${{I}_{0}}(t)$ между двумя последовательными импульсами ${{I}_{0}}(t)$ и характеризуется двумя максимумами с провалом, приходящимся на середину между этими импульсами ${{I}_{0}}(t)$.

Рисунок 4 иллюстрирует различия формы импульсов функций ${{P}_{{02}}}(t)$ и $\,{{\rho }_{{22}}}(t)$ в случае облучения частицы, характеризуемого отношением $\alpha = 2.$ При таком облучении на каждые два импульса облучения приходится по три импульса ${{P}_{{02}}}(t)$ и по три импульса $\,{{\rho }_{{22}}}(t).$ При этом второй – в этой тройке импульсов – импульс ${{P}_{{02}}}(t)$ и второй импульс $\,{{\rho }_{{22}}}(t)$ приходятся на интервал времени, характеризуемый минимальной интенсивностью между первым и вторым импульсом ${{I}_{0}}(t).$ Все импульсы ${{P}_{{02}}}(t)$ имеют одинаковую форму, а у каждого второго импульса $\,{{\rho }_{{22}}}(t)$ максимальное значение примерно в два раза меньше максимального значения первого импульса. На второй импульс облучения в каждой группе из трех импульсов ${{P}_{{02}}}(t)$ и $\,{{\rho }_{{22}}}(t)$ приходится по одному импульсу ${{P}_{{02}}}(t)$ и одному импульсу $\,{{\rho }_{{22}}}(t),$ которые немного отстают от импульса ${{I}_{0}}(t),$ и их интенсивности спадают до нуля одновременно со спаданием до нуля этого второго импульса ${{I}_{0}}(t).$ Такая картина повторяется для каждых двух последующих импульсов ${{I}_{0}}(t)$ – 3‑го и 4-го, 5-го и 6-го и т.д.

Приведенные рисунки иллюстрируют различия динамики возбуждения частицы, предсказываемые моделированием на основе формализма КТСС для поглощения одного из фотонов бихроматического облучения и на основе формализма ОУБ при тех же условиях облучения, характеризуемых параметрами $\Omega $ и ${{\Omega }_{R}}.$ Как можно заключить по виду этих рисунков (и по виду полученных других аналогичных рисунков, которые не приведены), при определенной интенсивности облучения, характеризуемой значением ${{\Omega }_{R}},$ эти различия тем меньше, чем больше расстройка резонанса $\left( \Omega \right)$ частоты каждой из компонент поля облучения с частотой собственного перехода частицы. Этого и следовало ожидать, имея в виду установленную в [10] такую же закономерность различия результатов моделирования двумя применяемыми методами заселенности возбужденного состояния частицы при облучении монохроматическим облучением.

Представляет интерес экспериментально проверить отмеченные закономерности. В связи с этим заметим, что экспериментальные данные измерения заселенности возбужденного состояния ³P₁ атома Yb при облучении бихроматическими полями с различными значениями разности начальных фаз монохроматических компонент поля, которые получены в отмеченной во Введении работе [8], по мнению авторов этой работы, находятся в согласии с результатами моделирования, проведенного на основе использования численного решения соответствующей системы оптических уравнений Блоха.

ЗАКЛЮЧЕНИЕ

Установлено, что динамика возбуждения двухуровневой частицы бихроматическим электромагнитным полем, описываемая на основе теории составной системы из частицы и двухмодового квантованного поля излучения, в общем случае значительно отличается от соответствующей динамики, описываемой на основе применения оптических уравнений Блоха. Это следует иметь в виду при теоретическом описании упомянутых во Введении эффектов преобразования веществом бихроматического поля, при интерпретации механизма рассматриваемого фотовозбуждения вещества бихроматическим полем и при изучении возможности совершенствования методов оптимального квантового управления ходом фотопревращений молекул импульсами разного вида.