Химическая физика, 2019, T. 38, № 9, стр. 71-77
Бифуркации течения псевдопластических жидкостей в канале с резким сужением и расширением
С. А. Патлажан 1, *, Д. Е. Рощин 2, 3, И. В. Кравченко 2, А. А. Берлин 1
1 Институт химической физики им. Н.Н. Семёнова Российской академии наук
Москва, Россия
2 Институт проблем химической физики Российской академии наук
Черноголовка, Россия
3 Московский физико-технический институт
Долгопрудный, Россия
* E-mail: sapat@yandex.ru
Поступила в редакцию 15.03.2019
После доработки 15.03.2019
Принята к публикации 20.03.2019
Аннотация
Методами численного моделирования изучены условия бифуркационных переходов при течении псевдопластических жидкостей в канале с резким сужением и расширением. Реологические свойства рассматриваемых неньютоновских жидкостей описывались моделью Карро–Ясуда. Построены бифуркационные диаграммы течения для сред с разными кривыми вязкости. Показано, что значения критического числа Рейнольдса в точке бифуркации и размеры образующихся угловых вихрей существенно зависят от характера кривой вязкости.
ВВЕДЕНИЕ
Каналы с переменным поперечным сечением находят широкое применение в различных областях науки и технологии. В частности, они используются для формирования высокоскоростных струй [1, 2] и более однородного перемешивания смесей несовместимых полимеров [3]. Особый интерес представляет применение таких каналов для турбулизации течения при небольших числах Рейнольдса [4–6]. Такие течения благоприятствуют интенсификации теплообмена [7, 8] и значительному увеличению эффективности работы химических реакторов [9, 10]. Частным случаем является канал с резким сужением и расширением, и в литературе можно найти достаточно много работ, посвященых исследованию структуры течений различных жидкостей в таких каналах (см., например, [3, 5, 11–17]). Исследования показали, что на выходе из зоны сужения образуются вихри, симметрия которых может нарушаться при увеличении числа Рейнольдса. Такое резкое изменение структуры течения называют бифуркацией. Дальнейшее увеличение числа Рейнольдса приводит к каскаду бифуркационных переходов с образованием все новых вихрей разных размеров вплоть до возникновения развитого турбулентного течения.
С учетом использования каналов с переменным сечением для переноса расплавов и растворов полимеров представляет значительный интерес исследовать их транспортные свойства. В данной работе ограничимся рассмотрением псевдопластических жидкостей. К ним относятся расплавы олигомеров и разбавленные растворы полиакриламида [18], ксантановой камеди [19] и карбоксиметил целлюлозы [20], а также суспезии с анизодиаметрической формой частиц, кровь [21]. Упругой реакцией таких жидкостей можно пренебречь, однако их вязкость, как правило, уменьшается с ростом скорости сдвига.
Для моделирования реологических свойств неупругих псевдопластических жидкостей зачастую используют степенную модель вязкости:
где $\eta \left( {\dot {\gamma }} \right)$ – динамическая вязкость, $\dot {\gamma }$ – скорость сдвига, а $K,$ n – параметры модели. Для псевдопластичных сред n < 1 [15–17, 22, 23]. Соотношение (1) использовалось также для описания течения псевдопластических сред в канале с резким сужением и расширением [15–17, 24]. Однако данная модель имеет ряд недостатков. В частности, она предсказывает неограниченное увеличение вязкости с уменьшением скорости сдвига и не описывает переход к ньютоновской жидкости с постоянной вязкостью, который наблюдается для большинства псевдопластических жидкостей. Кроме того, согласно (1), при больших скоростях сдвига вязкость стремится к нулю. Этих недостатков лишена модель Карро–Ясуда:(2)
$\eta \left( {\dot {\gamma }} \right) = {{\eta }_{\infty }} + \left( {{{\eta }_{0}} - {{\eta }_{\infty }}} \right){{\left[ {1 + {{{\left( {\lambda \dot {\gamma }} \right)}}^{a}}} \right]}^{{{{\left( {n - 1} \right)} \mathord{\left/ {\vphantom {{\left( {n - 1} \right)} a}} \right. \kern-0em} a}}}}.$Параметр λ определяет скорость сдвига, при которой ньютоновское плато переходит в область снижения вязкости. При малых и больших скоростях сдвига $\dot {\gamma }$ вязкость такой модели остается конечной и принимает значения ${{\eta }_{0}}$ и ${{\eta }_{\infty }}$ соответственно. При больших скоростях сдвига и достаточно малой вязкости ${{\eta }_{\infty }}$ (${{\left( {\lambda \dot {\gamma }} \right)}^{a}} \gg 1$ и ${{\eta }_{\infty }}~ \to 0$) соотношение Карро–Ясуда (2) переходит в модель степенной жидкости (1):
Таким образом, $K = {{\eta }_{0}}{{\lambda }^{{n - 1}}}.$ Модель Карро–Ясуда успешно использовалась для описания реологических свойств псевдопластических сред [18–21], в том числе при течении в каналах с резким сужением и расширением при достаточно малых числах Рейнольдса [12].
Цель настоящей работы – изучение структуры течения в канале с резким сужением и расширением на примере псевдопластических жидкостей, реологические поведение которых описывается моделью Карро–Ясуда, соответствующих разным кривым вязкости. Мы не ограничиваемся исследованием симметричной моды течения, но также рассматриваем условия возникновения бифуркационных переходов к асимметричной картине течения. Подробно исследуются особенности бифуркаций течения (критические числа Рейнольдса и размеры угловых вихрей) различных псевдопластических жидкостей.
МОДЕЛЬ И МЕТОДЫ РЕШЕНИЯ
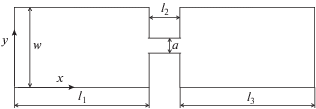
Течение псевдопластической жидкости рассматривалось в 2D-канале с резким сужением и расширением (рис. 1). Канал состоит из двух широких камер одинаковой ширины w = 0.03 м, длиной l1 = l3 = 0.15 м и узкого зазора между ними шириной a = 0.002 м и длиной l2 = 0.01 м. Таким образом, относительное сужение составило w/a = 15. Начало координат отсчитывалось от нижнего левого угла канала. Поэтому вход в сужение лежит при x = 0.15 м. Центральная линия канала соответствует y = 0.015 м.
Скорость u и давление p несжимаемой псевдопластичной жидкости описываются уравнениями Навье–Стокса и условием несжимаемости:
(3)
$\rho \left[ {\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \left( {{\mathbf{u}}\nabla } \right){\mathbf{u}}} \right] = - \nabla p + 2\nabla \left[ {\eta \left( {{{I}_{2}}} \right){\mathbf{D}}} \right],$Здесь ${\mathbf{D}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\left( {\nabla {\mathbf{u}} + {{{\left( {\nabla {\mathbf{u}}} \right)}}^{T}}} \right)$ – тензор скоростей деформаций, а $\rho $ – плотность жидкости, которая принята равной 1000 кг/м3. В каналах сложной геометрии вязкость $\eta \left( {{{I}_{2}}} \right)$ неньютоновской жидкости удобно рассматривать как функцию второго инварианта тензора скоростей деформаций ${{I}_{2}} = {\mathbf{D}}~:{\mathbf{D}}.$ В этом случае соотношение (2) Карро–Ясуда представляется в виде
(4)
$\eta \left( {{{I}_{2}}} \right) = ~{{\eta }_{\infty }} + \left( {{{\eta }_{0}} - {{\eta }_{\infty }}} \right)[1 + {{\left( {2{{\lambda }^{2}}{{I}_{2}}{{)}^{{{a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}}}}} \right]}^{{{{\left( {n - 1} \right)} \mathord{\left/ {\vphantom {{\left( {n - 1} \right)} a}} \right. \kern-0em} a}}}}.$При течении простого сдвига соотношения (2) и (4) совпадают. На входе в канал задавалась постоянная скорость течения, а на выходе – постоянное давление и нулевой градиент скорости. На твердых стенках выполнялось условие прилипания: ${{{\mathbf{u}}}_{{wall}}} = 0.$
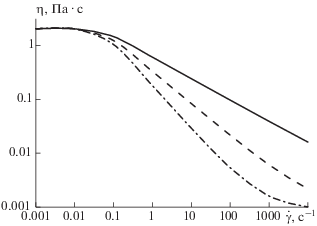
В качестве модельной жидкости в данной работе рассматривался 0.2%-ный (по массе) водный раствор ксантановой камеди, для которого ${{\eta }_{0}}$ = = 2.05 Па ⋅ с, ${{\eta }_{\infty }}$ = 0.00089 Па ⋅ с, $\lambda $ = 21.2 с, а = 2 и n = 0.406 [25]. Кривая вязкости такой среды соответствует штриховой линии на рис. 2. Сплошная и штрих-пунктирная линии соответствуют n = 0.6 и 0.2. Видно, что уменьшение параметра n приводит к более сильной зависимости вязкости от скорости сдвига, что соответствует большему наклону кривой вязкости.
Рис. 2.
Кривые вязкости для разных значений показателя n модели Карро–Ясуда: n = 0.6 (сплошная линия), 0.4 (штриховая – 0.2%-ный (по массе) раствор ксантановой камеди), 0.2 (штрих-пунктир).
Число Рейнольдса определяли формулой
(5)
${\text{Re}} = {{\rho \bar {u}w} \mathord{\left/ {\vphantom {{\rho \bar {u}w} {{{{\bar {\eta }}}_{w}}}}} \right. \kern-0em} {{{{\bar {\eta }}}_{w}}}},$(6)
${{\bar {\eta }}_{w}} = ~{{\eta }_{\infty }} + \left( {{{\eta }_{0}} - {{\eta }_{\infty }}} \right)[1 + {{\left( {\lambda \bar {u}{{w}^{{ - 1}}}{{)}^{a}}} \right]}^{{{{\left( {n - 1} \right)} \mathord{\left/ {\vphantom {{\left( {n - 1} \right)} a}} \right. \kern-0em} a}}}}.$При n = 1 ${{\bar {\eta }}_{w}} = ~{{\eta }_{0}}$ и формула (5) переходит в классическое определение числа Рейнольдса для ньютоновской жидкости с вязкостью ${{\eta }_{0}}.$
Систему уравнений (3) совместно с реологической моделью (4) решали в рамках открытой вычислительной платформы OpenFoam [26] при помощи метода конечных объемов и алгоритма PISO. На расчетную область накладывали регулярные прямоугольные сетки. С целью исследования влияния густоты сетки на получаемые решения провели расчеты для ньютоновской жидкости при Re = 16 для разного числа ячеек. Определили размеры l1 и l2 угловых вихрей, образующихся на выходе из узкой части канала в асимметричном режиме течения. В табл. 1 эти величины представлены в безразмерном виде относительно ширины канала L1 = l1/w и L2= l2/w. Видно, что, начиная с числа ячеек 1185 × 256, решение перестает заметно зависеть от густоты сетки. Такая расчетная сетка была использована в данной работе для дальнейших расчетов.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
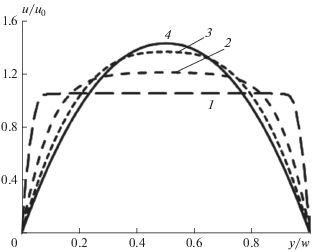
Вначале рассмотрели профили скорости установившегося течения ньютоновской и ряда псевдопластических жидкостей Карро–Ясуда при разных значениях показателя n (соотношение (4)). В средней части входной камеры канала (x = 0.08 м) распределения скорости практически совпадают с таковыми в бесконечно длинной плоской щели. В частности, профиль скорости ньютоновской жидкости (n = 1) соответствует течению Пуазейля (параболическое распределение), а при n = 0 распределение скорости принимает пробкообразную форму (рис. 3). Отметим, что в последнем случае средняя скорость течения $\bar {u}$ близка к скорости в широкой части профиля. При 0 < n < 1 профили скорости занимают промежуточные положения. Представленные на рис. 3 профили скорости течения соответствуют $\bar {u}$ = 0.25 м/с. Они согласуется с результатами, полученным в работе [22] для $n \in \left[ {0.3;\,\,1} \right].$
Рис. 3.
Профили скоростей в широкой части канала для жидкостей с различным показателем степени n: 1 – n = 0, 2 – n = 0.4, 3 – n = 0.6, 4 – n = 0.9. Средняя скорость $\bar {u}$ = 0.25 м/с.
При достаточно малых числах Re на выходе из зоны сужения формируются симметричные угловые вихри как для ньютоновских, так и для псевдопластических жидкостей. Их размеры возрастают по мере увеличения Re до тех пор, пока не достигнуто некоторое критическое число Рейнольдса Recr, выше которого симметричная картина течения резко нарушается и один из вихрей становится больше другого – возникает асимметричное течение. Такой бифуркационный переход продемонстрирован на рис. 4 на примере псевдопластичной среды Карро–Ясуда при n = 0.6, для которой, как оказалось, Recr = 3.06.
Рис. 4.
Линии тока при течении жидкости Карро–Ясуда через канал с резким сужением и расширением при различных числах Рейнольдса, n = 0.6, Recr = 3.06: Re/Recr = 0.60 (a), 1.00 (б), 1.07 (в), 1.29 (г), 1.76 (д).

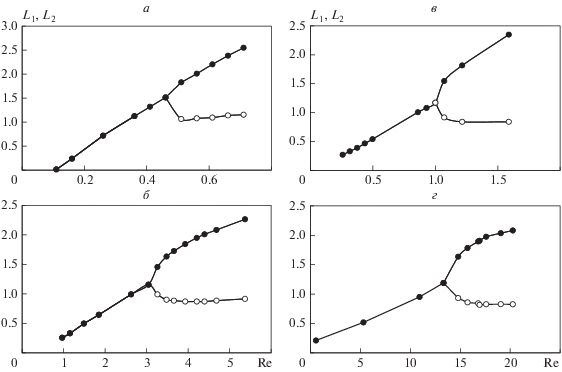
Для количественной оценки данного эффекта построили бифуркационные диаграммы в форме зависимости относительных размеров L1= l1/w и L2= l2/w угловых вихрей от числа Рейнольдса Re для разных значений показателя n = 0, 0.6, 0.9 и 1 (рис. 5). Видно, что с увеличением числа Рейнольдса размер большего вихря продолжает расти, в то время как меньший вихрь практически не изменяется, а его наибольший размер меньше критической длины Lcr в точке бифуркации. Рисунок 5 также показывает, что уменьшение n приводит к заметному снижению критического числа Рейнольдса Recr. Другими словами, у псевдопластических жидкостей бифуркационный переход происходит при гораздо меньших числах Рейнольдса по сравнению с ньютоновской жидкостью.
Рис. 5.
Бифуркационные диаграммы для разных псевдопластических и ньютоновской жидкостей: n = 0 (a), 0.6 (б), 0.8 (в), 1 [25] (г).
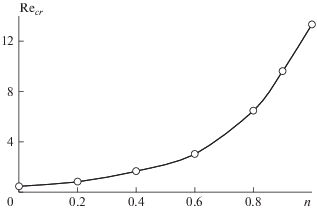
Это подтверждает рис. 6, который показывает, что Recr экспоненциально спадает при уменьшении показателя n, которое соответствует росту угла наклона кривой вязкости (см. рис. 2). Зависимость Recr от n хорошо аппроксимируется соотношением Recr = 0.43e3.4n. Это говорит о том, что по сравнению с ньютоновскими жидкостями течение псевдопластических сред в каналах с резким сужением и расширением гораздо менее устойчиво.
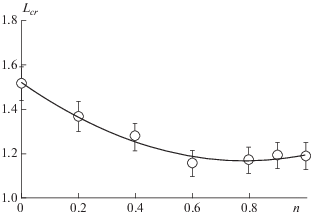
Интересно отметить, что в точке бифуркации максимальные значения относительных размеров вихрей Lcr также зависят от типа жидкости, т.е величины показателя n в соотношении Карро–Ясуда (4). Эта зависимость приведена на рис. 7. Из графика можно сделать вывод, что при n > 0.6 критический размер вихрей практически не зависит от n и его значение составляет примерно 1.175. При n < 0.6 величина Lcr начинает расти вплоть до максимального значения при n = 0.
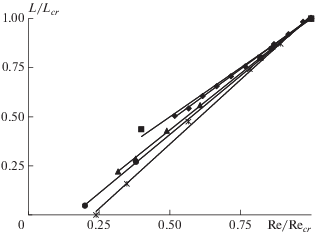
Поскольку для рассмотренных псевдопластичных жидкостей критические значения размеров вихрей Lcr и чисел Рейнольдса Recr сильно различаются, представляет интерес преобразовать бифуркационные диаграммы на рис. 5 в относительных координатах L/Lcr и Re/Recr . В этом случае все диаграммы имеют общую точку ветвления (рис. 8). При этом в асимметричной моде течения размер меньшего вихря практически не зависит от показателя n. Он примерно одинаков для ньютоновской (n = 1) и рассмотренных псевдопластичных жидкостей при $0 \leqslant n < 1.$ В то же время длина наибольшего вихря растет относительно Lcr с увеличением n. В симметричном режиме течения (Re < Recr) относительный размер угловых вихрей также увеличивается с увеличением числа Рейнольдса. Этот фрагмент диаграммы показан на рис. 9 в большем увеличении. Видно, что в этом случае зависимости L/Lcr от Re/Recr хорошо аппроксимируются линейной зависимостью при любом n:
(7)
$\frac{L}{{{{L}_{{cr}}}}} = \alpha \left( n \right)\frac{{{\text{Re}}}}{{{\text{R}}{{{\text{e}}}_{{cr}}}}} + \beta \left( n \right).$Рис. 8.
Совмещенная бифуркационная диаграмма для ньютоновской и разных псевдопластических жидкостей: * – n = 0, ⚪ – n = 0.4, △ – n = 0.6, ◇ – n = 0.9, ◻ – n = 1.
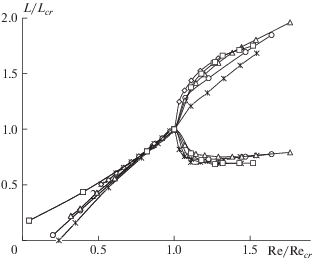
Рис. 9.
Совмещенная бифуркационная диаграмма при Re ≤ Recr: * – n = 0, ⚫ – n = 0.4, ▲ – n = 0.6, ◆ – n = 0.9, ◼ – n = 1.
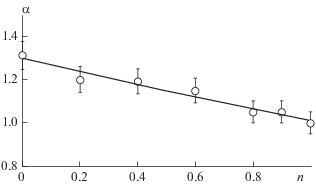
Значения параметров α и β представлены в табл. 2 при разных n, а на рис. 10 показана зависимость $\alpha \left( n \right).$ Видно, что с увеличением n (уменьшением угла наклона кривой вязкости (см. рис. 2) скорость роста вихрей уменьшается линейно.
ЗАКЛЮЧЕНИЕ
Методами численного моделирования в данной работе изучены особенности бифуркационных переходов различных псевдопластических сред в канале с резким сужением и расширением. Показано, что в точке бифуркации симметричное положение угловых вихрей скачкообразно переходит в асимметричное состояние, при котором их размеры становятся разными. Установлено, что с уменьшением показателя степени n в модели Карро–Ясуда, отвечающего за скорость уменьшения вязкости с ростом скорости сдвига, критическое число Рейнольдса Recr экспоненциально уменьшается. Последнее обстоятельство свидетельствует о том, что в канале с переменным сечением течение псевдопластических сред менее устойчиво по сравнению с ньютоновскими жидкостями. Совмещенная бифуркационная диаграмма в координатах относительного размера вихрей L/Lcr и относительного числа Рейнольдса Re/Recr показала, что в ассимметричном режиме течения размер меньшего из вихрей практически не зависит от вида кривой вязкости или параметра n, тогда как с его уменьшением относительный размер L/Lcr большего вихря снижается. В режиме симметричного течения относительный размер угловых вихрей линейно возрастает с ростом Re/Recr . Таким образом, перемешивание жидкостей в каналах с резким сужением и расширением, которое ассоциируется с динамикой вихрей на выходе из узкой зоны, существенно зависит от типа кривой вязкости.
Численные расчеты проводились с использованием вычислительных ресурсов Межведомственного суперкомпьютерного центра РАН.
Научно-исследовательская работа выполнена за счет субсидии, выделенной ИХФ РАН на выполнение государственного задания (тема № 0082-2014-0013) и ИПХФ РАН (тема № 0089-2019-0001), а также за счет гранта Российского фонда фундаментальных исследований № 18-29-17072.
Список литературы
Eggers J., Villermaux E. // Rep. Prog. Phys. 2008. V. 71. P. 036601.
Litvinenko Y.A., Grek G.R., Kozlov G.V. et al. // EUCASS Proc. Ser. 2012. V. 3. P. 429.
Rondin J., Bouquey M., Muller R. et al. // Polym. Eng. Sci. 2014. V. 54. P. 1444.
Oliveira M.S.N., Rodd L.E., McKinley G.H. et al. // Microfluid. Nanofluid. 2008. V. 5. P. 809.
Tsai C.H., Chen H.T., Wang Y.N. et al. // Ibid. 2007. V. 3. № 1. P. 13.
Kravchenko I.V., Patlazhan S.A., Muller R. et al. // J. Phys. Conf. Ser. 2016. V. 774. № 1. P. 012026.
Konoplev A.A., Aleksanyan G.G., Rytov B.L. et al. // Theor Found. Chem. Eng. 2007. V. 41. P. 526.
Motaharinezhad M., Shahraki S., Tirgar R. et al. // Indian J. Sci. Res. 2014. V. 1. P. 47.
Minsker K.S., Berlin A.A., Zakharov V.P., Zaikov G.E. Fast Liquid-Phase Processes in Turbulent Flows. Utrecht, Boston: Taylor & Francis, 2004.
Dong L., Shufen Z. Intern. // J. Chem. React. Eng. 2014. V. 12. P. 465.
Cherdron W., Durst F., Whitelaw J.H. // J. Fluid Mech. 1978. V. 84. P. 1. P. 13.
Poole R.J., Escudier M.P., Oliveira P.J. // Proc. Royal Soc. London Ser. A. 2005. V. 461. P. 3827.
Oliveira P.J. // J. Non-Newton. Fluid Mech. 2009. V. 160. P. 40.
Lanzaro A., Yuan X.F. // Ibid. 2011. V. 166. P. 1064.
Ternik P. // Ibid. 2009. V. 157. P. 15.
Ternik P. // Ibid. 2010. V. 165. P. 1400.
Dhinakaran S., Oliveira M.S.N., Pinho F.T. et al. // Ibid. 2013. V. 198. P. 48.
Balan C.M., Balan C. // U.P.B. Sci. Bull. Ser. D. 2010. V. 72. P. 121.
Haase A.S., Wood J.A., Sprakel L.M.J. et al. // Phys. Rev. E. 2017. V. 95. № 2. P. 023105.
Al-Habahbeh A.A. Simulations of Newtonian and non-Newtonian flows in deformable tubes. PhD thesis. Michigan Technological University, 2013.
Boyd J., Buick J.M., Green S. // Phys. Fluids 2007. V. 19. № 9. P. 093103.
Wang L., Tian F.-B. // Appl. Sci. 2018. V. 8. P. 559.
Pravesh R., Dhiman A., Bharti R.P. // J. Brazil. Soc. Mech. Sci. Eng. 2019. V. 41. P. 88.
Manica R., De Bortoli A.L. // J. Non-Newton. Fluid Mech. 2004. V. 121. P. 35.
Патлажан С.А., Кравченко И.В., Мюллер Р. // Докл. АН. 2017. Т. 473. № 2. С. 163.
Weller H.G., Tabor G., Jasak H. et al. // Comput. Phys. 1998. V. 12. P. 620.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика