Химическая физика, 2020, T. 39, № 10, стр. 9-19
Расчет низшего резонансного 1S-состояния иона Н– методом комплексного абсорбирующего потенциала
С. О. Адамсон 1, *, Д. Д. Харлампиди 2, Г. В. Голубков 1, 3, Ю. А. Дьяков 1, И. И. Морозов 1, Д. В. Шестаков 1, М. Г. Голубков 1
1 Федеральный исследовательский центр химической физики
им. Н.Н. Семёнова Российской академии наук
Москва, Россия
2 Московский педагогический государственный университет
Москва, Россия
3 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
* E-mail: sergey.o.adamson@gmail.com
Поступила в редакцию 07.05.2020
После доработки 07.05.2020
Принята к публикации 20.05.2020
Аннотация
На примере низшего резонанса аниона H– установлено, что расчетные значения энергии и ширины резонанса, найденные в результате поиска оптимальной точки в методе комплексного абсорбирующего потенциала, содержат систематическую ошибку, величина которой зависит от параметров абсорбирующего потенциала и приближения, используемого для решения уравнения Шредингера. Показано, что точность расчета параметров резонанса может быть повышена, если процедуру поиска оптимальной точки заменить усреднением по области закручивания траектории.
1. ВВЕДЕНИЕ
В последние три десятилетия всплеск широкомасштабных исследований физико-химических процессов в D- и E-слоях ионосферы объясняется возросшим интересом к процессам распространения электромагнитных сигналов со спутников и радиолокационных станций. Фундаментальную роль в формировании спектров радиосигналов играют химические реакции и радиационные процессы с участием ридберговских молекул [1]. При повышении солнечной активности эти реакции ответственны за формирование неравновесной двухтемпературной плазмы и степень ее ионизации. К ним относятся реакции диссоциативной рекомбинации и ассоциативной ионизации, реакции обмена при столкновениях ридберговских частиц с атомами и молекулами нейтральной среды, реакция тушения высоковозбужденных частиц.
Искажение и задержка спутниковых сигналов при прохождении через D- и E-слои атмосферы происходит за счет резонансного рассеяния фотонов, движущихся в электромагнитном поле сигнала, на ридберговских комплексах, заселяемых в двухтемпературной неравновесной плазме [2, 3]. В итоге наблюдаются сдвиг несущей частоты сигнала и временнáя задержка его распространения. Это происходит в результате рассеяния ридберговского электрона на ионном остове и нейтральной молекуле среды в промежуточных автоионизационных состояниях составной системы [4].
Возможность оценки энергии и ширины резонансных состояний с помощью оптического потенциала [5] впервые была показана более тридцати лет назад. Несмотря на отсутствие строгого теоретического обоснования, для нескольких модельных систем были получены достаточно точные значения характеристик резонансов Брейта–Вигнера [6–11]. Позднее, в работах Рисса и Мейера [12, 13], было дано обоснование данного подхода, названного “методом комплексного абсорбирующего потенциала” (КАП). В дальнейшем этот метод неоднократно использовался для расчета резонансных состояний в многоатомных системах (молекулах и их ионах). Один из наиболее интересных примеров его применения – расчет резонансных состояний анионов двухатомных молекул N2 [12, 14–25], BF [26], H2 [16, 19], CO [17–19, 22, 23, 27], CuF и AgF [19, 28]. Метод КАП применялся также к расчетам анионов трехатомных молекул HCN [29], FCN [30] и анионов органических молекул от формальдегида [17, 18, 31] до парабензохинона [17–21, 29, 32–34], азотистых оснований [35]. В литературе встречаются примеры использования метода КАП для расчетов автоионизационных состояний нейтральных молекул H2 [20], димера фтороводорода (HF)2 [36] и дианиона ${\text{C}}_{{\text{2}}}^{{{\text{2}} - }}$ [37]. Интерес к атомам ограничился расчетами низшего резонансного состояния аниона Be– [22, 23].
При практической реализации метода КАП основное внимание уделялось учету эффектов электронной корреляции, что привело к появлению нескольких модификаций, различающихся по способам приближенного решения электронного уравнения Шредингера [14, 17–19, 21–25, 31, 34, 36, 38]. Однако точность используемых подходов можно сравнить только для низшего 2Πg-резонанса аниона ${\text{N}}_{2}^{ - }.$ В большинстве случаев оценки энергии низшего 2Πg-резонанса ${\text{N}}_{2}^{ - }$ для равновесного межъядерного расстояния хорошо согласуются между собой и превышают экспериментальное значение на 5–8% [14, 17, 18, 21, 22]. Несколько хуже согласуются с экспериментом оценки, полученные с применением теории возмущений, поскольку энергия резонанса оказывается заниженной на 9–18% [20]. Аналогичная ситуация наблюдается и для расчетных значений ширины резонанса.
Теоретический аппарат метода КАП позволяет численно исследовать поведение энергии системы в окрестности резонансного полюса, задавая матрицу рассеяния в аналитической форме [12]. Получая аналогичную зависимость из приближенного решения уравнения Шредингера для атома или его аниона, можно проверить выполнение условий, необходимых для успешного расчета энергии и ширины резонанса методом КАП. В качестве модельной системы для сравнения может быть выбран атом или его анион с несколькими электронами, для расчетов резонансов которого не потребуется высоких вычислительных затрат. В настоящем исследовании в качестве модельной системы использовался анион Н−.
В разд. 2 работы в краткой форме дано теоретическое обоснование метода КАП. В разд. 3 подробно описан метод расчета, а в разд. 4 обсуждаются полученные результаты.
2. ТЕОРИЯ
В методе комплексного абсорбирующего потенциала гамильтониан системы $\hat {H}\left( \eta \right)$ представляется в виде
где ${{\hat {H}}_{0}}$ – исходный гамильтониан системы, η – действительный параметр и $W$ – абсорбирующий потенциал, вид которого зависит от исходного гамильтониана системы. В частности, для единственной частицы, движущейся в одномерном потенциале, абсорбирующий потенциал будет удовлетворять условиям(2)
$W = \left\{ {{\begin{gathered} {\text{0,}}\,\,\,\,r < {{R}_{0}}, \hfill \\ \operatorname{Re} \left( {W\left( r \right)} \right) > {\text{0,}}\,\,\,\,r \geqslant {{R}_{{\text{0}}}}, \hfill \\ \end{gathered} }} \right.$При малых значениях параметра η энергия рассматриваемой системы, $E\left( \eta \right),$ предполагается непрерывной (дифференцируемой) функцией, удовлетворяющей стационарному уравнению
где ψ – собственная функция. В окрестности резонанса с энергией ${{E}_{{res}}} = {{E}_{0}} - i{\Gamma \mathord{\left/ {\vphantom {\Gamma 2}} \right. \kern-0em} 2}$ (E0 – энергия, Γ – ширина резонанса), $E\left( \eta \right)$ описывается формальным рядом:(4)
$E\left( \eta \right) = {{E}_{{res}}} + {{a}_{1}}\eta + {{a}_{2}}{{\eta }^{2}} + {{a}_{3}}{{\eta }^{3}} + ...;$Ключевым элементом теории является возможность аппроксимации η-траектории рядом (4), что показывается на простой модельной задаче. Сначала в атомной системе единиц ($\hbar = e = {{m}_{e}} = 1$) вводится радиальный гамильтониан вида
(6)
$\hat {H}\left( \eta \right) = - \frac{1}{2}\frac{{{{d}^{2}}}}{{d{{r}^{2}}}} + V\left( r \right) - i\eta W\left( {r,{{R}_{0}}} \right),$(7)
$\begin{gathered} ik{{\left. {\frac{{\psi \left( {E\left( \eta \right),\eta ,r} \right)}}{{{{\psi }^{/}}\left( {E\left( \eta \right),\eta ,r} \right)}}} \right|}_{{r = {{R}_{0}} + 0}}} = \\ = - i{\text{tg}}\left( {\pi \left( {z + \frac{1}{4}} \right)} \right)\sqrt z \frac{{\Gamma \left( {z + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right)}}{{\Gamma \left( {z + {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}} \right)}}, \\ \end{gathered} $(9)
$\frac{{\exp \left\{ {2i\left( {k{{R}_{0}} + {{{\delta }}_{0}}} \right)} \right\}\left( {E - E_{{res}}^{*}} \right) - \left( {E - {{E}_{{res}}}} \right)}}{{\exp \left\{ {2i\left( {k{{R}_{0}} + {{{\delta }}_{0}}} \right)} \right\}\left( {E - E_{{res}}^{*}} \right) + \left( {E - {{E}_{{res}}}} \right)}} = g\left( z \right),$По предположению Рисса и Мейера, приближенное решение уравнения (3) вносит в функцию $E\left( \eta \right)$ ошибку, не мешающую поиску оптимальной точки по выбранному критерию (например, по минимуму функции (5)) [12]. Справедливость данного предположения авторы подтверждают примерами решения модельных задач и расчетами низшего 2Πg-резонанса аниона ${\text{N}}_{2}^{ - }.$
Из теоретического обоснования Рисса и Мейера следует, что расчет параметров резонанса методом КАП будет успешным, если при $E\left( \eta \right)\sim {{E}_{{res}}}$ будут одновременно выполняться два условия. Во-первых, при точном решении уравнения (3) оптимальная точка η-траектории $E\left( \eta \right),$ поиск которой проводится по выбранному критерию, должна быть единственной. Во-вторых, ошибка, возникающая при приближенном решении уравнения (3), должна быть пренебрежимо малой. Исследовать η-траекторию и проверить выполнимость первого условия можно при численном решении уравнения (9). Учитывая вид гамильтониана, использованного при выводе (9), выполнение второго условия можно проверить ab initio расчетом энергии атома или аниона с несколькими электронами. Здесь идеальным объектом для исследования является низший 1S-резонанс аниона H–, многократно исследовавшийся экспериментально и теоретически. Последующие части настоящего исследования посвящены решению уравнения (9) и ab initio расчетам низшего 1S-резонанса H–.
3. МЕТОД РАСЧЕТА
При численном решении уравнения (9) для матрицы рассеяния (8) были взяты параметры ${{\delta }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и ${{E}_{{res}}}$ = $3.42639031 - 0.01277448i$ а. е. Выбранное значение энергии резонанса совпадает с энергией низшего резонанса в модельном потенциале Бэйна [39]. Уравнение (9) решалось итерационно, с порогом сходимости по энергии, равным 10–9. Для вычисления входящих в правую часть (9) гамма-функций был использован метод, предложенный в монографии [40]. Положения оптимальных точек при решении модельной задачи и для аниона H– оценивались по минимуму функции (5).
Для H– модифицированный гамильтониан был взят в приближении бесконечно тяжелого ядра:
(10)
$\hat {H}\left( \eta \right) = - \frac{1}{2}\sum\limits_{i = 1}^2 {{{\Delta }_{i}}} - \sum\limits_{i = 1}^2 {\frac{1}{{{{r}_{i}}}}} + \frac{1}{{{{r}_{{12}}}}} - i\eta \sum\limits_{i = 1}^2 {W\left( {{{r}_{i}},{{R}_{0}}} \right)} ,$Уравнение Шредингера решалось методом ограниченного конфигурационного взаимодействия (ОКВ) [41–43], что позволяет сравнить КАП с методом стабилизации [41, 43]. В методе ОКВ матрица гамильтониана строилась в базисе конфигурационных функций состояния (КФС), для чего в базисе одночастичных функций (спин-орбиталей) $\left\{ {{{\psi }_{k}}} \right\}$ выделялся набор локализованных вблизи ядра (внутренних) функций $\left\{ {\psi _{k}^{\Gamma }} \right\},$ на которых далее строился полный набор КФС $\left\{ {\Phi _{i}^{\Gamma }\left( {1,..,N} \right)} \right\}.$ Оставшиеся (внешние) функции $\left\{ {\psi _{k}^{f}} \right\}$ использовались для построения КФС, однократно возбужденных относительно $\left\{ {\Phi _{i}^{\Gamma }\left( {1,..,N} \right)} \right\}.$ Необходимые для построения КФС спин-орбитали $\left\{ {{{\psi }_{k}}} \right\}$ представлялись как произведения спиновой и пространственных частей (орбиталей). В качестве последних были взяты ортонормированные функции
(12)
$\begin{gathered} {{\varphi }_{i}}(r,\theta ,\varphi ) = {{\left[ {{{{{b}^{3}}n!} \mathord{\left/ {\vphantom {{{{b}^{3}}n!} {\left( {n + 2l + 2} \right)!}}} \right. \kern-0em} {\left( {n + 2l + 2} \right)!}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,{{(br)}^{l}}{{e}^{{ - {{br} \mathord{\left/ {\vphantom {{br} 2}} \right. \kern-0em} 2}}}}L_{n}^{{2l + 2}}(br)Y_{l}^{M}(\theta ,\varphi ), \\ \end{gathered} $Точность расчета значений параметров резонанса (энергии и ширины) зависит от полноты (качества) базиса квадратично-интегрируемых функций, используемого для приближенного решения уравнения Шредингера. При решении модельных задач параметры резонанса быстро сходятся к точным значениям [44–47], но при решении электронной задачи неполнота базиса орбиталей проявляется в виде быстрых изменений энергии и ширины резонанса при малых изменениях базиса орбиталей, как было показано ранее для метода стабилизации [41, 42, 47]. Чтобы минимизировать влияние неполноты базиса орбиталей на результаты расчетов методом КАП, проводилось усреднение оценок на интервале значений масштабирующего множителя 0.9 ≤ b ≤ 1.8 с шагом ${{\Delta }b = {\text{0}}{\text{.1}}}.$ Выбор диапазона значений множителя был осуществлен на основании анализа расчетов низшего 1S-резонанса H– методом стабилизации (0.9 ≤ b ≤ 2.5, V0 = = 1 а.е., $10 \leqslant {{R}_{0}} \leqslant 75$ а.е., детали обработки графов приведены в работах [41, 43]). Как показано в табл. 1, отклонения вычисленных значений энергии и ширины резонанса (Rres ~ 25.3 а.е.) от средних величин оказались незначительными ($\sim {\kern 1pt} {{10}^{{ - 5}}}$ а.е.), что позволило снизить вычислительные затраты в расчетах методом КАП за счет понижения верхней границы диапазона значений масштабирующего множителя. Для каждого из значений масштабирующего множителя параметр η варьировался в диапазоне $ - 12.0 \leqslant \ln \eta \leqslant 3.0$ с шагом $\Delta \ln \eta = 0.05.$ Далее, если не оговорено особо, под значениями параметров резонанса подразумеваются их средние значения
Таблица 1.
Энергия ${{\bar {E}}_{{res}}}$ и полуширина ${{\bar {\Gamma }} \mathord{\left/ {\vphantom {{\bar {\Gamma }} 2}} \right. \kern-0em} 2}$ низшего 1S-резонанса Н−, рассчитанные методом стабилизации
| Метод | Базис | ${{\bar {E}}_{{res}}}$ | $\Delta {{\bar {E}}_{{res}}}$ | ${{\bar {\Gamma }} \mathord{\left/ {\vphantom {{\bar {\Gamma }} 2}} \right. \kern-0em} 2}$ | ${{\Delta \bar {\Gamma }} \mathord{\left/ {\vphantom {{\Delta \bar {\Gamma }} 2}} \right. \kern-0em} 2}$ |
|---|---|---|---|---|---|
| ОКВ | (9.2/18.2) | 0.35126 | 1 | 89 | 1 |
| (9.2/22.2) | 0.35126 | 1 | 89 | 1 | |
| (9.2/26.2) | 0.35126 | 0 | 89 | 1 | |
| ПКВ | (27.1) | 0.35167 | 1 | 91 | 2 |
| (31.1) | 0.35167 | 0 | 91 | 0 | |
| (27.2)* | 0.35126 | 1 | 89 | 1 | |
| (31.2)* | 0.35126 | 1 | 89 | 1 | |
| Референсное значение** | – | 0.35122025 | – | 89.35 | – |
Примечание: ${{\bar {\Gamma }} \mathord{\left/ {\vphantom {{\bar {\Gamma }} 2}} \right. \kern-0em} 2},$ $\Delta {{\bar {E}}_{{res}}}$ и ${{\Delta \bar {\Gamma }} \mathord{\left/ {\vphantom {{\Delta \bar {\Gamma }} 2}} \right. \kern-0em} 2}$ приведены в 10–5 а.е. * Расчет методом полного конфигурационного взаимодействия (ПКВ) [43]. **Расчет, проведенный в работе [48].
4. РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
При применении метода КАП к реальным системам (молекулам, атомам и их ионам) пределу $\eta = 0$ должен соответствовать набор дискретных уровней с действительными энергиями, отвечающих интегрируемым с квадратом приближенным решениям уравнения (3). Напротив, если полагать параметр η действительным положительным числом, то в пределе $\eta \to 0$ входящее в правую часть (9) отношение гамма-функций можно заменить асимптотическим рядом [49, 50]:
(13)
${{\Gamma \left( {z + \frac{1}{4}} \right)} \mathord{\left/ {\vphantom {{\Gamma \left( {z + \frac{1}{4}} \right)} {\Gamma \left( {z + \frac{3}{4}} \right)}}} \right. \kern-0em} {\Gamma \left( {z + \frac{3}{4}} \right)}} = \frac{1}{{\sqrt z }}\left( {1 - \frac{1}{{64{{z}^{2}}}} + o\left( {{{z}^{{ - 4}}}} \right)} \right),$Анализ решений уравнения (9) показывает, что в методе КАП могут возникать траектории с одной или несколькими областями закручивания в окрестности резонанса. К первому типу следует отнести и траектории, соответствующие $\beta = 0.$ В обоих случаях резонанс находится в области закручивания, но вид траекторий зависит от выбора параметра ${{R}_{0}}$ (рис. 1). Соответственно, траектории первого типа имеют одну оптимальную точку (точку минимума функции (5)), а траектории второго типа – две. Оптимальные точки всегда находятся в областях закручивания и не совпадают с резонансом. Отметим, что варьирование параметров ${{R}_{0}}$ и $\beta $ слабо влияет на значение масштабирующего множителя $\alpha = \operatorname{Re} \eta ,$ отвечающего оптимальной точке (рис. 2).
Рис. 1.
Поведение η-траекторий в модельной задаче для различных значений R0 (а.е.): а) ⚪ – R0 = 3.0 (β = 0.23), ◻ – R0 = 5.0 (β = 0.23), ◇ – R0 = 7.0 (β = 0.23), штрих-пунктирная линия – R0 = 5.0 (β = 0); б) ⚪ – R0 = 2.0 (β = 0.10), ◻ – R0 = 4.0 (β = 0.10), ◇ – R0 = 6.0 (β = 0.10), штрих-пунктирная линия – R0 = 4.0 (β = 0). Закрашенными кругами (⚫) обозначены оптимальные точки. Знак “+” указывает на точное положение резонанса.
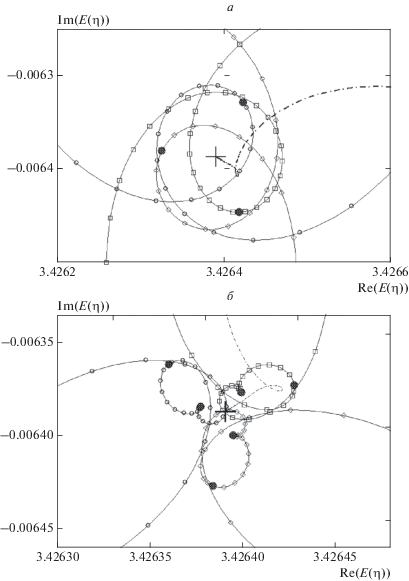
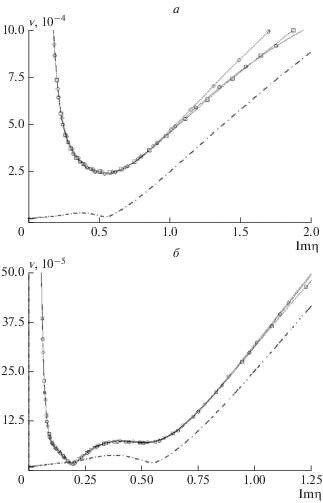
Рис. 2.
Вид функции v(η) (выражение (5)) в модельной задаче для различных значений R0 (а.е.): а) ⚪ – R0 = 3.0 (β = 0.23), ◻ – R0 = 5.0 (β = 0.23), ◇ – R0 = 7.0 (β = 0.23), штрих-пунктирная линия ‑ R0 = 5.0 (β = 0); б) ⚪ – R0 = 2.0 (β = 0.10), ◻ – R0 = 4.0 (β = 0.10), ◇ – R0 = 6.0 (β = 0.10), штрих-пунктирная линия – R0 = 4.0 (β = 0).
Исследование η-траекторий, построенных для аниона H–, показало, что они имеют одну область закручивания, захватывающую резонанс и несколько оптимальных точек, из которых только одна находится в области закручивания (рис. 3). При этом в область закручивания траектории не всегда попадает оптимальная точка, соответствующая минимальному значению параметра η. Функции ${v}\left( \eta \right)$ в случае низшего 1S-резонанса иона Н– имеют более сложный вид по сравнению с модельной задачей: количество оптимальных точек и их положения зависят от параметров КАП (рис. 4). Из сравнения траекторий, построенных для модельной задачи и аниона H–, видно, что единственным признаком близости траектории к резонансу является наличие области ее закручивания с внутренней оптимальной точкой. Этот вывод можно переформулировать иначе: в окрестности резонанса траектория должна иметь точки пересечения, для которых выполняется условие
(14)
$E\left( {{{\eta }_{1}}} \right) = E\left( {{{\eta }_{2}}} \right),\,\,\,\,{{\eta }_{1}} \ne {{\eta }_{2}}.$Рис. 3.
Поведение η-траекторий в окрестности низшего 1S-резонанса иона Н–, соответствующих комплексным адсорбирующим потенциалам (11): а – КАП2; б – КАП4. В обоих случаях расчеты проведены с использованием базиса орбиталей (9.2/26.1) и масштабирующего множителя b = 1.4 для различных точек наложения КАП: ⚪ – R0 = 20 а. е., ◻ – R0 = 25 а. е., ◇ – R0 = 30 а. е. Черными кружками обозначены оптимальные точки. Знак “+” указывает на положение резонанса, рассчитанное в [48].
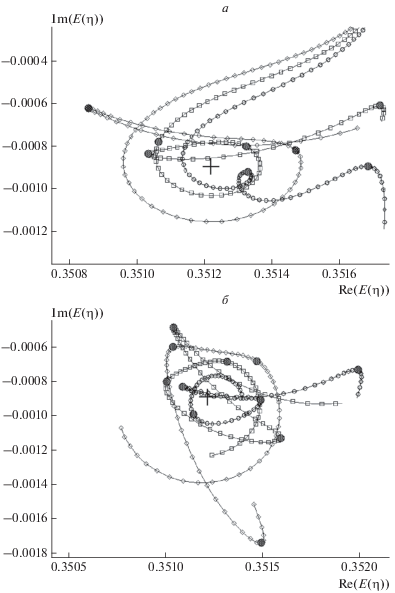
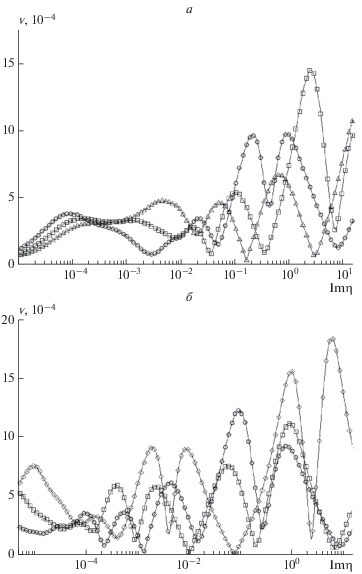
Рис. 4.
Вид функций ${v}\left( \eta \right)$ (см. выражение (5)) в случае низшего 1S-резонанса иона Н–, соответствующих комплексным адсорбирующим потенциалам (11): а – КАП2, б – КАП4. Расчеты проведены с использованием базиса орбиталей (9.2/26.1) и масштабирующего множителя b = 1.4 для различных точек наложения КАП: ⚪ – R0 = 20 а.е., ◻ – R0 = = 25 а.е., ◇ – R0 = 30 а.е.
Как уже отмечалось выше, при решении модельной задачи оптимальная точка не совпадает с резонансом, что должно приводить к систематической ошибке при вычислении параметров резонанса. Для модельной задачи величину ошибки можно полагать незначительной – относительные ошибки расчета энергии резонанса не превышали 0.01%, а ширины – 2%. Чтобы выяснить, изменяется ли величина ошибки при приближенном решении уравнения Шредингера, были проведены расчеты параметров резонанса H–.
Для получения величин энергии и ширины резонанса было использовано усреднение по области закручивания (метод А) η-траектории. При усреднении предполагалось, что расстояния между соседними точками траектории одинаковые, что позволило заменить поиск центра масс [8] расчетом среднего значения. Для сравнения также применялся поиск оптимальной точки внутри области закручивания (метод Б).
На основании анализа результатов расчетов можно сделать вывод о большей точности метода А по сравнению с методом Б (табл. 2 и 3). Лучшее согласие с референсными значениями энергии и ширины [48] наблюдается для ${{R}_{0}} \geqslant 25$ а.е. в базисах максимального размера. Переход от потенциала КАП2 к КАП4 не приводит к значительному изменению средних значений ширины и энергии, но разброс мгновенных значений в последнем случае больше.
Таблица 2.
Энергия ${{\bar {E}}_{{res}}}$ и полуширина ${{\bar {\Gamma }} \mathord{\left/ {\vphantom {{\bar {\Gamma }} 2}} \right. \kern-0em} 2}$ низшего 1S-резонанса Н−, рассчитанные с потенциалом КАП2 для усреднения по траектории и поиска оптимальной точки
| Nin, lin | Nex, lex | Метод А | Метод Б | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ${{\bar {E}}_{{res}}}$ | $\Delta {{\bar {E}}_{{res}}}$ | ${{\bar {\Gamma }} \mathord{\left/ {\vphantom {{\bar {\Gamma }} 2}} \right. \kern-0em} 2}$ | ${{\Delta \bar {\Gamma }} \mathord{\left/ {\vphantom {{\Delta \bar {\Gamma }} 2}} \right. \kern-0em} 2}$ | ${{\bar {E}}_{{res}}}$ | $\Delta {{\bar {E}}_{{res}}}$ | ${{\bar {\Gamma }} \mathord{\left/ {\vphantom {{\bar {\Gamma }} 2}} \right. \kern-0em} 2}$ | ${{\Delta \bar {\Gamma }} \mathord{\left/ {\vphantom {{\Delta \bar {\Gamma }} 2}} \right. \kern-0em} 2}$ | ||
| R0 = 20 | |||||||||
| 9, 2 | 18, 1 | 0.35144 | 4 | 102 | 11 | 0.35144 | 17 | 82 | 5 |
| 26, 1 | 0.35133 | 3 | 94 | 1 | 0.35133 | 5 | 88 | 5 | |
| 9, 2 | 18, 2 | 0.35144 | 4 | 102 | 11 | 0.35144 | 18 | 82 | 5 |
| 26, 2 | 0.35134 | 3 | 94 | 1 | 0.35133 | 5 | 88 | 5 | |
| 9, 3 | 18, 2 | 0.35143 | 4 | 102 | 11 | 0.35143 | 18 | 82 | 5 |
| 26, 2 | 0.35133 | 3 | 93 | 1 | 0.35132 | 5 | 88 | 5 | |
| R0 = 25 | |||||||||
| 9, 2 | 18, 1 | 0.35131 | 8 | 87 | 7 | 0.35139 | 40 | 78 | 30 |
| 26, 1 | 0.35122 | 1 | 88 | 1 | 0.35121 | 8 | 82 | 12 | |
| 9, 2 | 18, 2 | 0.35134 | 5 | 86 | 6 | 0.35139 | 26 | 59 | 6 |
| 26, 2 | 0.35123 | 1 | 88 | 1 | 0.35121 | 8 | 82 | 12 | |
| 9, 3 | 18, 2 | 0.35133 | 5 | 86 | 6 | 0.35138 | 26 | 59 | 5 |
| 26, 2 | 0.35122 | 1 | 88 | 1 | 0.35120 | 8 | 82 | 12 | |
| R0 = 30 | |||||||||
| 9, 2 | 18, 1 | 0.35129 | 8 | 91 | 8 | 0.35150 | 34 | 50 | 10 |
| 26, 1 | 0.35119 | 4 | 91 | 3 | 0.35130 | 13 | 80 | 19 | |
| 9, 2 | 18, 2 | 0.35129 | 8 | 91 | 8 | 0.35150 | 34 | 50 | 9 |
| 26, 2 | 0.35119 | 4 | 91 | 3 | 0.35130 | 13 | 80 | 19 | |
| 9, 3 | 18, 2 | 0.35128 | 8 | 91 | 8 | 0.35149 | 34 | 50 | 9 |
| 26, 2 | 0.35118 | 4 | 90 | 3 | 0.35129 | 13 | 80 | 19 | |
Таблица 3.
Энергия ${{\bar {E}}_{{res}}}$ и полуширина ${{\bar {\Gamma }} \mathord{\left/ {\vphantom {{\bar {\Gamma }} 2}} \right. \kern-0em} 2}$ низшего 1S-резонанса Н−, рассчитанные с потенциалом КАП4 для усреднения по траектории и поиска оптимальной точки
| Nin, lin | Nex, lex | Метод А | Метод Б | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ${{\bar {E}}_{{res}}}$ | $\Delta {{\bar {E}}_{{res}}}$ | ${{\bar {\Gamma }} \mathord{\left/ {\vphantom {{\bar {\Gamma }} 2}} \right. \kern-0em} 2}$ | ${{\Delta \bar {\Gamma }} \mathord{\left/ {\vphantom {{\Delta \bar {\Gamma }} 2}} \right. \kern-0em} 2}$ | ${{\bar {E}}_{{res}}}$ | $\Delta {{\bar {E}}_{{res}}}$ | ${{\bar {\Gamma }} \mathord{\left/ {\vphantom {{\bar {\Gamma }} 2}} \right. \kern-0em} 2}$ | ${{\Delta \bar {\Gamma }} \mathord{\left/ {\vphantom {{\Delta \bar {\Gamma }} 2}} \right. \kern-0em} 2}$ | ||
| R0 = 20 | |||||||||
| 9, 2 | 18, 1 | 0.35135 | 6 | 89 | 5 | 0.35129 | 22 | 68 | 6 |
| 26, 1 | 0.35129 | 2 | 90 | 1 | 0.35125 | 12 | 83 | 5 | |
| R0 = 25 | |||||||||
| 9, 2 | 18, 1 | 0.35123 | 6 | 86 | 6 | 0.35110 | 19 | 54 | 10 |
| 26, 1 | 0.35126 | 2 | 88 | 2 | 0.35128 | 13 | 68 | 4 | |
| R0 = 30 | |||||||||
| 9, 2 | 18, 1 | 0.35122 | 8 | 84 | 10 | 0.35110 | 28 | 45 | 7 |
| 26, 1 | 0.35125 | 3 | 86 | 3 | 0.35132 | 26 | 65 | 8 | |
| R0 = 35 | |||||||||
| 9, 2 | 18, 1 | 0.35126 | 10 | 85 | 9 | 0.35122 | 40 | 38 | 6 |
| 26, 1 | 0.35126 | 4 | 86 | 5 | 0.35135 | 25 | 54 | 9 | |
Таким образом, в расчетах реальных систем поиск оптимальной точки [12] необходимо проводить для области ${{\eta }_{1}} \leqslant \eta \leqslant {{\eta }_{2}},$ где границы области поиска могут быть найдены из условия (14). Однако даже при его соблюдении расчетные значения параметров резонанса будут содержать систематическую ошибку, величина которой будет зависеть от параметров абсорбирующего потенциала и качества базиса орбиталей.
5. ЗАКЛЮЧЕНИЕ
Корректное описание процессов диссоциативной рекомбинации и ассоциативной ионизации основных атмосферных молекул в рамках теории многоканального квантового дефекта требует знания адиабатических потенциальных кривых и матричных элементов радиального неадиабатического связывания диссоциативных и ридберговских конфигураций молекул N2, O2, NO [52–54] для состояний, относящихся к низшим диссоциационным пределам. Рассчитываемые значения сечений и констант скорости реакций диссоциативной рекомбинации и ассоциативной ионизации оказываются очень чувствительными к точности определения положения и ширины резонансов.
В результате исследования, проведенного в настоящей работе, обнаружено, что расчетные значения энергии и ширины резонанса, найденные в результате поиска оптимальной точки в методе КАП, всегда содержат систематическую ошибку, величина которой зависит от параметров абсорбирующего потенциала и точности приближенного решения уравнения Шредингера. Ошибка расчета параметров резонанса может быть снижена при замене процедуры поиска оптимальной точки усреднением по области закручивания траектории. Но и в этом случае оценки параметров резонансов остаются чувствительными к выбору абсорбирующего потенциала.
Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (регистрационный номер АААА-А19-119010990034-5).
Список литературы
Kuverova V.V., Adamson S.O., Berlin A.A. et al. // Adv. Space Res. 2019. V. 64. № 10. P. 1876.
Голубков Г.В., Голубков М.Г., Манжелий М.И. // ДАН. 2013. Т. 452. № 5. С. 510.
Голубков Г.В., Куверова В.В., Озеров Г.К. и др. // Хим. физика. 2017. Т. 37. № 5. С. 63.
Голубков Г.В., Манжелий М.И., Эппельбаум Л.В. // Хим. физика. 2018. Т. 36. № 12. С. 12.
Bell J.S., Squires E.J. // Phys. Rev. Lett. 1959. V. 3. № 2. P. 96.
Jolicard G., Austin E.J. // Chem. Phys. Lett. 1985. V. 121. № 1–2. P. 106.
Jolicard G., Austin E.J. // Chem. Phys. 1986. V. 103. № 2–3. P. 295.
Jolicard G., Humbert J. // Ibid. 1987. V. 118. № 3. P. 397.
Jolicard G., Perrin M.Y. // Ibid. 1987. V. 116. № 1. P. 1.
Jolicard G., Leforestier C., Austin E.J. // J. Chem. Phys. 1988. V. 88. № 2. P. 1026.
Rom N., Lipkin N., Moiseyev N. // Chem. Phys. 1991. V. 151. № 2. P. 199.
Riss U.V., Meyer H.D. // J. Phys. B. 1993. V. 26. № 23. P. 4503.
Riss U.V., Meyer H.D. // Ibid. 1995. V. 28. № 8. P. 1475.
Sommerfeld T., Riss U.V., Meyer H.D. et al. // Ibid. 1998. V. 31. № 18. P. 4107.
Sommerfeld T., Cederbaum L.S. // Phys. Rev. Lett. 1998. V.80. № 17. P. 3723.
Jagau T.C., Krylov A.I. // J. Phys. Chem. Lett. 2014. V. 5. № 17. P. 3078.
Zuev D., Jagau T.C., Bravaya K.B. et al. // J. Chem. Phys. 2014. V. 141. № 2. 024102.
Zuev D., Jagau T.C., Bravaya K.B. et al. // Ibid. 2015. V. 143. № 14. 149901.
Jagau T.C., Krylov A.I. // Ibid. 2016. V. 144. № 5. 054113.
Kunitsa A.A., Granovsky A.A., Bravaya K.B. // Ibid. 2017. V. 146. № 18. 184107.
Feuerbacher S., Sommerfeld T., Santra R. et al. // Ibid. 2003. V. 118. № 14. P. 6188.
Jagau T.C., Zuev D., Bravaya K.B. et al. // J. Phys. Chem. Lett. 2014. V. 5. № 2. P. 310.
Jagau T.C., Zuev D., Bravaya K. B. et al. // Ibid. 2015. V. 6. № 19. P. 3866.
Sommerfeld T., Santra R. // Intern. J. Quant. Chem. 2001. V. 82. № 5. P. 218.
Sommerfeld T., Meyer H.D. // J. Phys. B. 2002. V. 35. № 8. P. 1841.
Dreuw A., Sommerfeld T., Cederbaum L.S. // J. Chem. Phys. 2002. V. 116. № 14. P. 6039.
Dreuw A., Sommerfeld T., Cederbaum L.S. // Theor. Chem. Acc. 1998. V. 100. № 1–4. P. 60.
Jagau T.C., Dao D.B., Holtgrewe N.S. et al. // J. Phys. Chem. Lett. 2015. V. 6. № 14. P. 2786.
Ehara M., Kanazawa Y., Sommerfeld T. // Chem. Phys. 2017. V. 482. P. 169.
Sommerfeld T. // Phys. Chem. Chem. Phys. 2001. V. 3. № 12. P. 2394.
Ehara M., Sommerfeld T. // Chem. Phys. Lett. 2012. V. 537. P. 107.
Sommerfeld T. // Phys. Chem. Chem. Phys. 2002. V. 4. № 12. P. 2511.
Kunitsa A.A., Bravaya K.B. // J. Phys. Chem. Lett. 2015. V. 6. № 6. P. 1053.
Ehara M., Fukuda R., Sommerfeld T. // J. Comp. Chem. 2016. V. 37. № 2. P. 242.
Kanazawa Y., Ehara M., Sommerfeld T. // J. Phys. Chem. A. 2016. V. 120. № 9. P. 1545.
Santra R., Cederbaum L.S., Meyer H.D. // Chem. Phys. Lett. 1999. V. 303. № 3–4. P. 413.
Sommerfeld T., Riss U.V., Meyer H.D. et al. // Phys. Rev. Lett. 1997. V. 79. № 7. P. 1237.
Jagau T.C., Bravaya K.B., Krylov A.I. // Ann. Rev. Phys. Chem. 2017. V. 68. P. 525.
Bain R.A., Bardsley J.N., Junker B.R. et al. // J. Phys. B. 1974. V. 7. № 16. P. 2189.
Zhang S., Jin J. Computation of Special Functions. New York: John Wiley & Sons, 1996.
Преображенская А.А., Адамсон С.О., Харлампиди Д.Д. и др. // Хим. физика. 2016. Т. 35. № 1. С. 65.
Адамсон С.О., Харлампиди Д.Д., Преображенская А.А. и др. // Хим. физика. 2017. Т. 36. № 12. С. 3.
Adamson S.O., Kharlampidi D.D., Dementiev A.I. // Advances in Quantum Methods and Applications in Chemistry, Physics, and Biology. Progress in Theoretical Chemistry and Physics. V. 27 / Eds. Hotokka M., Brandas E., Maruani J., Delgado–Barrio G. Cham: Springer, 2013. P. 101.
Adamson S., Kharlampidi D., Dementiev A. // J. Chem. Phys. 2008. V. 128. № 2. 024101.
Харлампиди Д.Д., Дементьев А.И., Адамсон С.О. // ЖФХ. 2010. Т. 84. № 4. С. 695.
Адамсон С.О., Харлампиди Д.Д., Дементьев А.И. // Хим. физика. 2011. Т. 30. № 11. С. 40.
Преображенская А.А., Адамсон С.О., Харлампиди Д.Д., Дементьев А.И. // Хим. физика. 2014. Т. 33. № 2. С. 27.
Bylicki M., Nicolaides C.A. // Phys. Rev. A. 2000. V. 61. № 5. P. 052509.
Tricomi F., Erdélyi A. // Pasific J. Math. 1951. V. 1. № 1. P. 133.
Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Т. 1. М.: Наука, 1973.
Zvijac D.J., Heller E.J., Light J.C. // J. Phys. B: At. Mol. Phys. 1975. V. 8. № 7. P. 1016.
Адамсон С.О., Куверова В.В., Озеров Г.К. и др. // Хим. физика. 2018. Т. 37. № 7. С. 3.
Адамсон С.О., Бюнкер Р.Дж., Голубков Г.В. и др. // Хим. физика. 2009. Т. 28. № 4. С. 26.
Golubkov M.G., Ozerov G.K., Adamson S.O. et al. // Chem. Phys. 2015. V. 462. P. 28.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика


