Химическая физика, 2020, T. 39, № 3, стр. 3-8
Полярон на решетке с ловушкой в приближении Су–Шриффера–Хигера
В. Н. Лихачев 1, Г. А. Виноградов 1, *
1 Институт биохимической физики им. Н.М. Эмануэля Российской академии наук
Москва, Россия
* E-mail: gvin@deom.chph.ras.ru
Поступила в редакцию 30.01.2019
После доработки 19.06.2019
Принята к публикации 20.06.2019
Аннотация
Волновая функция и энергия основного состояния для решетки с гамильтонианом Су–Шриффера–Хигера с ловушкой найдены тремя различными способами. Во-первых, путем численной минимизации функционала энергии. Во-вторых, с помощью построения вспомогательного гамильтониана, диагонализация которого определяет энергию основного состояния и волновые функции. В третьем аналитическом способе волновая функция полностью восстанавливается по асимптотике волновой функции. Все три подхода дают результаты, совпадающие с точностью 10–15.
ВВЕДЕНИЕ
При рассмотрении динамики поляронов в решеточных моделях широкое распространение получило приближение Су–Шриффера–Хигера (СШХ). Соответствующий гамильтониан был впервые записан при рассмотрении заряженного солитона в полиацетилене [1]. В дальнейшем, ввиду ясного физического смысла, простоты и эффективности, этот феноменологический подход широко использовался для изучения переноса заряда в различных неметаллических системах. Особый интерес вызывает перенос заряда в биологических системах, где представления о поляронном механизме являются доминирующими [2–8]. Баллистический перенос заряда в ДНК [9–11], когда его вероятность практически не зависит от длины цепи, также можно объяснить участием поляронов. Продолжается изучение переноса заряда в полиацетилене в приложенном внешнем электрическом поле [12–15].
Регулярная решетка без дефектов является скорее исключением. В большинстве систем присутствуют дефекты той или иной природы. Часто в роли дефектов выступают “ловушки”, т.е. узлы решетки, на которых сродство к электрону отличается от значений на других узлах, например разные основания ДНК. Такие дефекты носят название диагональных. Задачи для решеток с дефектами решаются в основном численными методами. Однако интересно знать функциональные зависимости электронных и транспортных свойств от параметров ловушек.
В настоящей работе задача о локализованном поляроне с гамильтонианом СШХ на решетке с диагональным дефектом решена тремя способами. Во-первых, энергия основного состояния получена путем численной минимизации исходного функционала энергии. Во втором способе построен вспомогательный гамильтониан, энергия основного состояния которого совпадает с энергией исходного гамильтониана. Волновая функция третьего, аналитического, решения построена, исходя из знания асимптотики волновой функции. Все три решения дают значения энергии основного состояния, совпадающие с точностью 10–15.
ПОСТАНОВКА ЗАДАЧИ. ОСНОВНОЕ СОСТОЯНИЕ СИСТЕМЫ
Рассматривается классическая гармоническая решетка, на которой находится один носитель заряда. Для определенности будем говорить об электроне, хотя подход годится и для дырочных носителей заряда. Гамильтониан рассматриваемой системы есть сумма гамильтониана решетки (Hlat) и электронного (He) гамильтониана:
Гамильтониан гармонической решетки имеет стандартный вид:
(2)
${{H}_{{lat}}} = \frac{1}{{2m}}\sum\limits_j {p_{j}^{2}} + \frac{k}{2}\sum\limits_j {y_{j}^{2}} ,\,\,\,\,{{y}_{j}} \equiv ({{x}_{{j + 1}}} - {{x}_{j}}).$Здесь m – масса частицы, k – жесткость связи, xj и pj – отклонение частицы на узле j от положения равновесия и ее импульс, yj – разность отклонений частиц.
Для описания волновой функции используется приближение сильной связи с переходами заряда только между ближайшими соседями. Электрон-фононное взаимодействие учитывается в приближении СШХ. Решетка бесконечна в обе стороны и однородна. На узле j = 0 находится ловушка глубиной U. Функционал энергии, соответствующий электронному гамильтониану, имеет вид
(3)
$\begin{gathered} {{H}_{e}} = - \sum\limits_j {({{t}_{0}} - \alpha {{y}_{j}})} \times \\ \times \,\,\left( {\Psi _{j}^{*}{{\Psi }_{{j + 1}}} + \Psi _{{j + 1}}^{*}{{\Psi }_{j}}} \right) - U\Psi _{0}^{2} + 2, \\ \end{gathered} $где t0 – интеграл перескока в равновесии, α – параметр электрон-фононного взаимодействия, Ψj – значение волновой функции на узле j. Ловушка локализует волновую функцию и служит дополнительным параметром задачи. Слагаемое “2” не влияет на конечные результаты и добавлено для того, чтобы дно зоны имело нулевую энергию. Для исключения несущественных параметров задачи и простоты удобно численно положить m = k = t0 = 1.С учетом того, что волновая функция Ψ основного состояния действительна, полная энергия системы представляется следующим функционалом:
(4)
$\begin{gathered} E = {{E}_{{lat}}} - 2\sum {{{\Psi }_{j}}{{\Psi }_{{j + 1}}}} + \\ + \,\,2\alpha \sum {{{y}_{j}}{{\Psi }_{{j + 1}}}{{\Psi }_{j}}} - U\Psi _{0}^{2} + 2. \\ \end{gathered} $Для безразмерных величин yj, U и α в (4) оставлены их прежние обозначения. Минимум функционала по импульсам дает pj = 0, а условие минимума по координатам позволяет выразить относительные смещения yj через волновые функции:
Подставляя это соотношение в функционал энергии (4), можно получить выражение для энергии в виде следующего функционала:
(6)
$\begin{gathered} E\{ \Psi \} = - 2\sum {{{\Psi }_{j}}{{\Psi }_{{j + 1}}}} - 2\beta \sum {{{{({{\Psi }_{j}}{{\Psi }_{{j + 1}}})}}^{2}}} - \\ - \,\,U\Psi _{0}^{2} + 2\sum \Psi _{j}^{2}, \\ \end{gathered} $где введено обозначение β = α2. Также для удобства последующего изложения по условию нормировки проведена замена второго слагаемого на $2\sum \Psi _{j}^{2}.$
Основное состояние получается как минимум функционала $E\{ \Psi \} $ по всем значениям волновой функции Ψj. Заметим, что если использовать стандартный градиентный метод спуска, то на каждом шаге необходимо восстанавливать нормировку волновой функции. Этого можно избежать, если использовать ту составляющую $\nabla E,$ которая перпендикулярна поверхности постоянной нормы. А именно, вместо градиента $\nabla E$ для минимизации целесообразно использовать выражение $\nabla E - \Psi (\Psi \nabla E).$ Также отметим, что, учитывая симметрию волновой функции относительно узла j = 0, можно вдвое уменьшить число переменных ${{\Psi }_{j}}.$ Подобная минимизация функционала энергии (6) позволяет определить волновые функции и энергию основного состояния E0.
ЭФФЕКТИВНЫЙ ГАМИЛЬТОНИАН
Рассмотрим другой способ нахождения энергии и волновой функции основного состояния рассматриваемой задачи. Основное состояние может быть получено как состояние с наименьшей энергией некоторого гамильтониана. Для этого запишем уравнения для минимума функционала $E\{ \Psi \} .$ Чтобы учесть нормировку, введем множитель Лагранжа μ. Минимизируемый функционал имеет вид
Получаем следующее уравнение для волновой функции (${{d{\kern 1pt} \Omega } \mathord{\left/ {\vphantom {{d{\kern 1pt} \Omega } {d{{\Psi }_{j}}}}} \right. \kern-0em} {d{{\Psi }_{j}}}} = 0$):
(8)
$\begin{gathered} 4{{\Psi }_{j}} - 2({{\Psi }_{{j - 1}}} + {{\Psi }_{{j + 1}}}) - 4\beta {\kern 1pt} {{\Psi }_{j}}\left( {\Psi _{{j - 1}}^{2} + \Psi _{{j + 1}}^{2}} \right) - \\ - \,\,2U{{\delta }_{{j,0}}}{{\Psi }_{0}} = 2\mu {{\Psi }_{j}}. \\ \end{gathered} $Оказывается, существует такой эффективный гамильтониан, основное состояние которого совпадает с искомой волновой функцией. Этот гамильтониан имеет вид
(9)
$\begin{gathered} {{{\tilde {H}}}_{{j,j}}} = 2 - U{{\delta }_{{j,0}}},\,\,\,\,{{{\tilde {H}}}_{{j,j + 1}}} = - 1 - 2\beta {{\Psi }_{j}}{{\Psi }_{{j + 1}}}, \\ {{{\tilde {H}}}_{{j + 1,j}}} = {{{\tilde {H}}}_{{j,j + 1}}}. \\ \end{gathered} $Уравнение Шредингера на собственные значения ${{E}_{{\tilde {H}}}}$ есть
(10)
$\begin{gathered} 2{{\Psi }_{j}} - {{\Psi }_{{j - 1}}} - {{\Psi }_{{j + 1}}} - \\ - \,\,2\beta {{\Psi }_{j}}\left( {\Psi _{{j - 1}}^{2} + \Psi _{{j + 1}}^{2}} \right) - U{{\delta }_{{j,0}}}{{\Psi }_{0}} = {{E}_{{\tilde {H}}}}{{\Psi }_{j}}. \\ \end{gathered} $Как видно, это уравнение (с точностью до множителя 2) совпадает с уравнением (8). При этом энергия ${{E}_{{\tilde {H}}}}$ равна множителю Лагранжа μ в (8). Волновая функция основного состояния находится с помощью стандартной программы диагонализации. В Приложении показано, каким образом получено выражение для гамильтониана (9). Подставляя полученное решение в (6), находим минимальную энергию E0 системы. Отметим, что если сравнить функционал энергии $E\{ \Psi \} $ и выражение для энергии ${{E}_{{\tilde {H}}}}$ $\left( {{{E}_{{\tilde {H}}}} = \left\langle {\Psi \left| {\tilde {H}} \right|\Psi } \right\rangle } \right),$ то получим
Отметим, что в случае отсутствия электрон-фононного взаимодействия (β = 0) волновая функция убывает экспоненциально: Ψj ~ q|j| (q < 1). При этом энергия равна
(12)
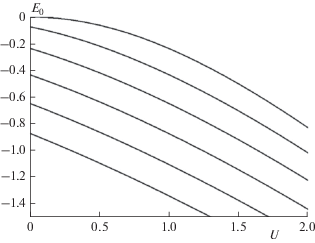
${{E}_{0}} = 2 - q - {{q}^{{ - 1}}},\,\,\,\,q \equiv 2{{\left[ {{{{\left( {4 + {{U}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + U} \right]}^{{ - 1}}}.$На рис. 1 показано поведение энергии E0 основного состояния в зависимости от глубины ловушки U для разных значений β.
Рис. 1.
Энергия основного состояния E0 в зависимости от глубины ловушки для разных значений β: сверху вниз – β = 0, 0.5, 1.0, …, 2.5. Для случая β = 0 использована формула (12).
ТОЧНОЕ РЕШЕНИЕ
Рассмотрим уравнение (8) для волновой функции (после его сокращения на 2):
(13)
$\begin{gathered} 2{{\Psi }_{j}} - ({{\Psi }_{{j - 1}}} + {{\Psi }_{{j + 1}}}) - 2\beta {{\Psi }_{j}}\left( {\Psi _{{j - 1}}^{2} + \Psi _{{j + 1}}^{2}} \right) - \\ - \,\,U{{\delta }_{{j,0}}}{{\Psi }_{0}} = \mu {{\Psi }_{j}}. \\ \end{gathered} $При |j| → ∞ нелинейные члены несущественны. Поэтому можно считать, что вдали от центра решетки волновая функция убывает экспоненциально: Ψj ~ Cq|j|, где C и q – новые параметры, которые будут определены ниже. При j $ \gg $ 1 нелинейными членами в (13) можно пренебречь. Тогда множитель Лагранжа μ выражается через q:
Удобно перенормировать волновую функцию следующим образом:
(15)
${{Y}_{j}} \equiv {{\Psi }_{j}}{{\beta }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$При этом параметр β исчезает из уравнений, но зато меняется нормировка:
Полагаем, что, начиная с некоторого номера узла j = K, волновая функция имеет экспоненциальную асимптотику, т.е. ищется в виде
где значения Y0, Y1, Y2, ….., YK – 1 подлежат определению. Для Yj при j ≥ 1 из (13) получаем систему квадратных уравнений:
(18)
$2{{Y}_{j}}Y_{{j - 1}}^{2} + {{Y}_{{j - 1}}} + {{Y}_{{j + 1}}} + 2{{Y}_{j}}Y_{{j + 1}}^{2} - (q + {{q}^{{ - 1}}}){{Y}_{j}} = 0.$Здесь и ниже сделана замена 2 – μ → q + q–1. Разрешая это уравнение относительно Yj – 1, получаем рекуррентные соотношения, которые позволяют выразить компоненты волновой функции через YK = CqK:
(19)
$\begin{gathered} {{Y}_{{j - 1}}} = - 2{{D}_{j}}{{\left[ {1 - 8{{Y}_{j}}{{D}_{j}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} + 1} \right]}^{{ - 1}}}, \\ {{D}_{j}} \equiv {{Y}_{{j + 1}}} + 2{{Y}_{j}}Y_{{j + 1}}^{2} - (q + {{q}^{{ - 1}}}){{Y}_{j}} \\ \end{gathered} $и j = K, K – 1, …., 2, 1, 0.
Рекуррентные соотношения (17) решаются следующим образом. На первом шаге используем YK + 1 = CqK + 1 и YK = CqK и из (19) находим значение YK-1. Далее аналогично по известным значениям YK и YK – 1 определяется YK – 2. Этот процесс рекурсии по уменьшающемуся номеру узла решетки повторяется, пока не будет получено значение Y0. Из уравнения (13) для Ψ0, заменив Ψ → Y, получaем значение параметра U:
(20)
$U = 2 - \mu + {{2{{Y}_{1}}} \mathord{\left/ {\vphantom {{2{{Y}_{1}}} {{{Y}_{0}}}}} \right. \kern-0em} {{{Y}_{0}}}} - 4Y_{1}^{2}.$Здесь использована симметрия волновой функции (Y–1 = Y1) Найденную волновую функцию подставляем в функционал энергии и находим минимальную энергию Е0 системы. Энергия E0 выражается через Yj следующим образом:
(21)
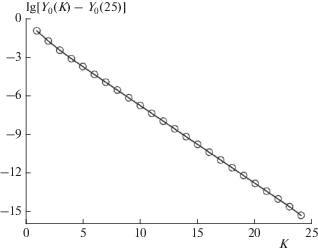
${{E}_{0}} = 2 - \left[ {UY_{0}^{2} + 4\sum\limits_0 {[{{Y}_{j}}{{Y}_{{j + 1}}} + {{{({{Y}_{j}}{{Y}_{{j + 1}}})}}^{2}}]} } \right]{{\beta }^{{ - 1}}}.$Очевидно, что чем большим выбрано значение K, тем точнее будет ответ для волновой функции. В качестве примера рассмотрен случай q = 0.5 и C = 1. При K ≥ 25 результаты стабилизируются – при этом достигается максимально возможная точность: ~10–15. Сходимость значения волновой функции Y0 к предельному значению экспоненциальная. Это показано на рис. 2.
Для рассмотренного случая (q = 0.5 и C = 1) мы сравнили энергии основного состояния, полученные тремя способами. Формулы (16) и (20) дают U = 0.390330452871901 и β = 0.675743099443042. Энергия E0, рассчитанная по формуле (21), равна E0 = –0.243612034324946. Энергия, полученная диагонализацией гамильтониана (формула (11)), отличается от этого значения на единицу в последнем знаке, а полученная минимизацией исходного функционала (4) – на две единицы в последнем знаке.
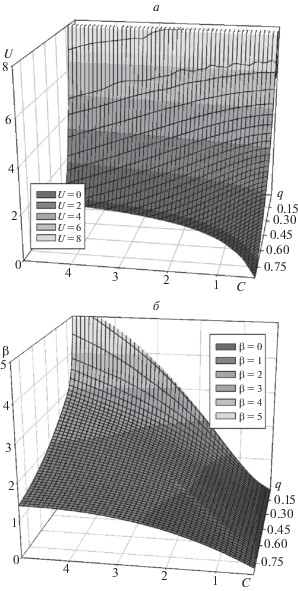
В исходном гамильтониане (1) присутствуют два параметра: β и U. Исходя из экспоненциальной асимптотики Yj ~ Cqj (j > K), волновая функция выражается через параметры C и q. Поэтому необходимо вернуться к исходным параметрам и найти связь между пáрами параметров {β, U} и {C, q}. Эта связь задается параметрически: из (16) определяется β, а из (20) – параметр U. На рис. 3 показаны зависимости параметров U и β от C и q.
Заметим, что показанные на рис. 3 зависимости построены только для случая U > 0, хотя графики формально могут быть продолжены и в область отрицательных значений U. Но это продолжение на самом деле не имеет смысла. Дело в том, что при отрицательных значениях U ловушка превращается в отталкивающий потенциал. При этом основное состояние – это полярон, отстоящий далеко от начала координат и потерявший связь с узлом j = 0. В этом легко убедиться, если начальную волновую функцию выбрать несимметричной относительно узла j = 0 (при минимизации функционала или при диагонализации гамильтониана).
ЗАКЛЮЧЕНИЕ
В настоящей работе решена задача о нахождении энергии основного состояния решетки с гамильтонианом Су–Шриффера–Хигера с дополнительным условием о существовании единственной ловушки глубиной U. Эта ловушка, в зависимости от знака, может служить притягивающим или отталкивающим центром. Решение получено тремя независимыми способами. В первом из них энергия основного состояния E0 получена путем численной минимизации функционала энергии исходного гамильтониана. Во втором способе предложен эффективный гамильтониан, отличающийся от исходного, энергия основного состояния которого совпадает с E0. Аналитическое выражение для волновой функции, являющееся третьим способом решения, построено по асимптотике этой волновой функции. Получены рекуррентные соотношения, которые связывают между собой волновые функции на соседних узлах решетки. Такая возможность есть следствие использования приближения сильной связи. Зная значения волновых функций в асимптотике, можно, используя рекурсию, получать значения волновых функций на решетке со сдвигающимся индексом номера решетки, пока не будет восстановлена вся волновая функция. Предлагаемый способ вычисления волновой функции по ее асимптотике можно назвать точным решением задачи. Все три использованных подхода дают результаты, совпадающие с точностью ~10–15.
Если в исходном гамильтониане дополнительно включить взаимодействия с дополнительными узлами (помимо ближайших соседей), например через один, то матрица гамильтониана станет пятидиагональной. Предложенный подход пригоден и для такого случая. При этом рекуррентные соотношения будут связывать между собой пять соседних волновых функций. Разработанный способ восстановления полной волновой функции по ее асимптотике пригоден и для других видов нелинейности.
Следует сделать несколько замечаний относительно применимости и эффективности предложенных способов решения задачи. Обычно используемый подход заключается в итерационном процессе решения исходного электронного гамильтониана (3). Для этого выбирается пробная геометрия решетки и полученный гамильтониан диагонализуется. В результате появляются новые значения волновых функций, которые подставляются в этот же гамильтониан. Эти итерации повторяются, пока не будет достигнута сходимость по энергии основного состояния. Однако не всегда итерационный процесс сходится. Причина в том, что при больших длинах решетки возникает квазивырождение уровней энергии и принадлежность волновых функций собственным значениям “перепутывается”. Именно по этой причине возникла необходимость разработать метод, лишенный этого недостатка. Оба предложенных численных подхода, хотя и являются вычислительно более трудоемкими, но гарантированно определяют энергию основного состояния и волновые функции.
Предложенные методы пригодны для решения одномерных задач в случае с одним носителем заряда (электрон или дырка). К этому классу задач относятся проблемы переноса заряда в полимерах, полипептидах, ДНК и других системах, у которых возникновение полярона может быть связано, например, с фотопереносом заряда.
Список литературы
Su W.P., Schrieffer J.R., Heeger A.J. // Phys. Rev. B. 1980. V. 22. № 4. P. 2099.
Conwell E.M., Rakhmanova S.V. // Proc. Natl. Ac. Sci. USA 2000. V. 97. № 9. P. 4556.
Conwell E.M., Basko D.M. // Synth. Metals 2003. V. 137. № 1–3. P. 1381.
Zhang G., Hu H., Cui Sh., Lv Z. // Physica B. 2010. V. 405. № 20. P. 4382.
Marchand D.J.J., De Filippis G., Cataudella V. et al. // Phys. Rev. Lett. 2010. V. 105. № 26. P. 266605.
Kucherov V.M., Kinz-Thompson C.D., Conwell E.M. // J. Phys. Chem. C. 2010. V. 114. № 3. P. 1663.
Lakhno V.D. // Intern. J. Quant. Chem. 2008. V. 108. № 11. P. 1971.
Лахно В.Д., Султанов В.Б. // Математическая биология и биоинформатика. 2009. V. 4. № 2. P. 46.
Augustyn K.E., Genereux J.C., Barton J.K. // Angew. Chem. Intern. Ed. 2007. V. 46. № 30. P. 5731.
Genereux J.C., Barton J.K. // Chem. Rev. 2010. V. 110. № 3. P. 1642.
Slinker J.D., Muren N.B., Renfrew S.E., Barton J.K. // Nature Chem. 2011. V. 3. № 3. P. 228.
Ono Y., Terai A. // J. Phys. Soc. Jap. 1990. V. 59. № 8. P. 2893.
Johansson A.A., Stafström S. // Phys. Rev. B. 2004. V. 69. № 23. P. 235205.
Yao Y., Qiu Y., Wu Ch.-Q. // J. Phys.: Condens. Matter. 2011. V. 23. № 30. P. 305401.
Astakhova T., Vinogradov G. // Europ. Chem. Bull. 2018. V. 7. № 4–6. P. 172.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика