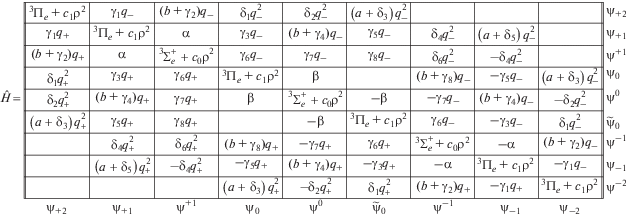Химическая физика, 2020, T. 39, № 3, стр. 9-16
Вибронное и спин-орбитальное взаимодействия электронных состояний 3Π и 3Σ+ в линейных трехатомных молекулах
В. М. Волохов 1, *, Л. В. Полуянов 1
1 Институт проблем химической физики Российской академии наук
Черноголовка, Россия
* E-mail: vvm@icp.ac.ru
Поступила в редакцию 06.02.2019
После доработки 06.02.2019
Принята к публикации 20.05.2019
Аннотация
В работе предложена двухэлектронная модель, описывающая вибронное и спин-орбитальное взаимодействия электронных состояний 3Π и 3Σ+ в линейных трехатомных молекулах. Анализ основан на использовании ab initio оператора Брейта–Паули для спин-орбитального взаимодействия. Показано, что операторы симметрии электронного гамильтониана включают как пространственные операции (которые действуют на электронные координаты), так и матричные операции (которые действуют на спины электронов). В нашем анализе принимаются в расчет только деформационные π-моды, и результирующая вибронная матрица 9 × 9 фактически описывает релятивистский псевдо-эффект Реннера типа (3Π + 3Σ+) × π. Собственные значения вибронной матрицы (т.е. поверхности потенциальной энергии) имеют аксиальную симметрию, однако не могут быть представлены аналитическими выражениями. Рассчитанный вибронный гамильтониан включает шесть электростатических и 16 спин-орбитальных вещественных параметров.
ВВЕДЕНИЕ
В нерелятивистской теории электронные состояния 3Π и 3Σ+ линейной трехатомной молекулы взаимодействуют посредством деформационных π-мод, что выражается вибронной матрицей 3 × 3 [1]. При учете спин-орбитального взаимодействия число базисных электронных состояний, формирующих вибронную матрицу, возрастает в три раза. В результате вибронное и спин-орбитальное взаимодействия электронных состояний 3Π и 3Σ+ описываются вибронной матрицей 9 × 9, зависящей от деформационных π-мод и содержащей как электростатические (нерелятивистские), так и спин-орбитальные (релятивисткие) вещественные параметры.
В данной работе мы предлагаем двухэлектронную модель взаимодействия 3Π и 3Σ+ с учетом только деформационных π-мод и спин-орбитального взаимодействия в электронном гамильтониане в форме ab initio оператора Брейта–Паули [2]. Поскольку функциональный вид результирующей вибронной матрицы определяется только свойствами симметрии системы и соответствующими квантовыми числами [3], то двухэлектронная модель взаимодействия состояний 3Π и 3Σ+ может быть применена и к многоэлектронным линейным трехатомным молекулам с четным числом электронов и тремя различными атомами. От числа электронов будут зависеть только значения постоянных вещественных параметров вибронной матрицы [4].
Взаимодействие состояний 3Π и 3Σ+ проявляется наиболее существенно, когда в молекулярном спектре электронные состояния 3Π и 3Σ+ являются соседними и разделены сравнительно небольшим энергетическим интервалом. В этом случае взаимодействие 3Π и 3Σ+ фактически представляет собой релятивистский псевдо-эффект Реннера типа (3Π + 3Σ+) × π. Эффект взаимодействия становится наиболее сильным в окрестности возможного пересечения электронных термов 3Π и 3Σ+ линейной трехатомной молекулы.
СИММЕТРИЯ ДВУХЭЛЕКТРОННОГО ГАМИЛЬТОНИАНА
Основным релятивистским эффектом в реннеровских системах является спин-орбитальное взаимодействие. С учетом последнего электронный гамильтониан представлен в виде суммы двух операторов – электростатического гамильтониана ${{\hat {H}}_{{es}}}$ и спин-орбитального оператора Брейта–Паули ${{\hat {H}}_{{so}}}{\text{:}}$
Мы не приводим здесь детальный вид операторов ${{\hat {H}}_{{es}}}$ и ${{\hat {H}}_{{so}}};$ последние представлены во многих публикациях и хорошо известны [2–6].
Если молекула имеет линейную форму, то электронный гамильтониан (1) характеризуется группой симметрии C∞v. Операторы этой группы, коммутирующие с гамильтонианом $\hat {H},$ имеют вид
(2)
$\hat {G}_{z}^{\varepsilon } = {{\hat {C}}_{1}}\left( \varepsilon \right){{\hat {C}}_{2}}\left( \varepsilon \right){{\left( {\begin{array}{*{20}{c}} {{{e}^{{{{i\varepsilon } \mathord{\left/ {\vphantom {{i\varepsilon } 2}} \right. \kern-0em} 2}}}}}&0 \\ 0&{{{e}^{{{{ - i\varepsilon } \mathord{\left/ {\vphantom {{ - i\varepsilon } 2}} \right. \kern-0em} 2}}}}} \end{array}} \right)}_{1}}{{\left( {\begin{array}{*{20}{c}} {{{e}^{{{{i\varepsilon } \mathord{\left/ {\vphantom {{i\varepsilon } 2}} \right. \kern-0em} 2}}}}}&0 \\ 0&{{{e}^{{{{ - i\varepsilon } \mathord{\left/ {\vphantom {{ - i\varepsilon } 2}} \right. \kern-0em} 2}}}}} \end{array}} \right)}_{2}},$(3)
${{\hat {Z}}_{\sigma }} = \hat {\sigma }_{{xz}}^{{(1)}}\hat {\sigma }_{{xz}}^{{(2)}}{{\left( {\begin{array}{*{20}{c}} 0&1 \\ { - 1}&0 \end{array}} \right)}_{1}}{{\left( {\begin{array}{*{20}{c}} 0&1 \\ { - 1}&0 \end{array}} \right)}_{2}},$где индексы “1” и “2” в правых частях (2) и (3) указывают, на какой электрон воздействует тот или иной оператор.
Пространственно-матричные двухэлектронные операторы $\hat {G}_{z}^{\varepsilon }$ и ${{\hat {Z}}_{\sigma }}$ соответствуют повороту на угол ε вокруг молекулярной оси $z\left( {\hat {G}_{z}^{\varepsilon }} \right)$ и отражению в вертикальной плоскости $xz({{\hat {Z}}_{\sigma }}).$ Они действуют как на координаты электронов, так и на операторы электронных спинов (матрицы Паули) в электронном гамильтониане $\hat {H}.$
Помимо этих пространственно-матричных операторов симметрии, электронный гамильтониан $\hat {H}$ характеризуется еще одним оператором симметрии – оператором обращения времени [7]; в частности, $\hat {H}$ коммутирует с оператором
(4)
$\hat {T} = {{\left( {\begin{array}{*{20}{c}} 0&{ - i} \\ i&0 \end{array}} \right)}_{1}}{{\left( {\begin{array}{*{20}{c}} 0&{ - i} \\ i&0 \end{array}} \right)}_{2}}\widehat {{\text{c}}{\text{.c}}{\text{.}}}\,,$где $\widehat {{\text{c}}{\text{.c}}{\text{.}}}$ – оператор комплексного сопряжения.
Отметим, что оператор обращения времени $\hat {T}$ является антиунитарным [7]. Для рассматриваемой модели с четным числом электронов имеет место равенство ${{T}^{2}}$ = +1.
РАЗЛОЖЕНИЕ ЭЛЕКТРОННОГО ГАМИЛЬТОНИАНА В РЯД ТЕЙЛОРА
Разложение электронного гамильтониана в ряд Тейлора по π-модам удобно вести в терминах величин, принадлежащих неприводимым представлениям группы симметрии C∞v. В табл. 1 мы приводим соответствующие симметризованные комбинации вплоть до вкладов второго порядка по π-модам.
Разложение электростатического гамильтониана в ряд Тейлора имеет вид
где ${{\hat {H}}_{0}}$ – нерелятивистский (электростатический) гамильтониан линейной молекулы,
(6)
${{\hat {H}}_{1}} = {{\hat {H}}_{ + }}\left( {{{\pi }_{ - }}} \right){{q}_{ + }} + {{\hat {H}}_{ - }}\left( {{{\pi }_{ + }}} \right){{q}_{ - }}\,,$(7)
${{\hat {H}}_{2}} = {{\hat {H}}_{{ + + }}}\left( {{{\delta }_{ - }}} \right)q_{ + }^{2} + {{\hat {H}}_{{ - - }}}\left( {{{\delta }_{ + }}} \right)q_{ - }^{2} + {{\hat {H}}_{{ + - }}}\left( {{{\sigma }^{ + }}} \right){{q}_{ + }}{{q}_{ - }}~.$В терминах симметризованных комбинаций из табл. 1 ряд Тейлора для спин-орбитального взаимодействия выглядит следующим образом:
Таблица 1.
Симметризованные комбинации нормальных мод и матриц Паули
| Порядок | Номер комбинации | Симметрия | Тип | Симметризованные комбинации |
|---|---|---|---|---|
| 1-й орбитальный | 1 | π | q | ${{q}_{ + }} = {{q}_{x}} + i{{q}_{y}},\,\,{{q}_{ - }} = {{q}_{x}} - i{{q}_{y}}$ |
| 2-й орбитальный | 2 | σ+ | ${{q}_{ + }}{{q}_{ - }}$ | |
| 3 | δ | $q_{ + }^{2},~\,q_{ - }^{2}$ | ||
| 0-й спин-орбитальный | 4, 5 | σ– | σ | $\hat {\sigma }_{z}^{{\left( 1 \right)}},\,\,\hat {\sigma }_{z}^{{\left( 2 \right)}}~$ |
| 6 | π | σ | $\hat {\sigma }_{ + }^{{\left( 1 \right)}} = \frac{{\hat {\sigma }_{y}^{{\left( 1 \right)}} - i\hat {\sigma }_{x}^{{\left( 1 \right)}}}}{2},\,\,\hat {\sigma }_{ - }^{{\left( 1 \right)}} = \frac{{\hat {\sigma }_{y}^{{\left( 1 \right)}} + i\hat {\sigma }_{x}^{{\left( 1 \right)}}}}{2}$ | |
| 7 | $\hat {\sigma }_{ + }^{{\left( 2 \right)}} = \frac{{\hat {\sigma }_{y}^{{\left( 2 \right)}} - i\hat {\sigma }_{x}^{{\left( 2 \right)}}}}{2},\,\,\hat {\sigma }_{ - }^{{\left( 2 \right)}} = \frac{{\hat {\sigma }_{y}^{{\left( 2 \right)}} + i\hat {\sigma }_{x}^{{\left( 2 \right)}}}}{2}$ | |||
| 1-й спин-орбитальный | 8, 9 k = 1, 2 | σ+ | qσ | ${{q}_{ - }}\hat {\sigma }_{ + }^{{\left( k \right)}} + {{q}_{ + }}\hat {\sigma }_{ - }^{{\left( k \right)}}$ |
| 10, 11 k = 1, 2 | σ– | qσ | ${{q}_{ - }}\hat {\sigma }_{ + }^{{\left( k \right)}} - {{q}_{ + }}\hat {\sigma }_{ - }^{{\left( k \right)}}$ | |
| 12, 13 k = 1, 2 | π | qσ | ${{q}_{ + }}\hat {\sigma }_{z}^{{\left( k \right)}},\,\, - {{q}_{ - }}\hat {\sigma }_{z}^{{\left( k \right)}}$ | |
| 14, 15 k = 1, 2 | δ | qσ | ${{q}_{ + }}\hat {\sigma }_{ + }^{{\left( k \right)}},\,\,{{q}_{ - }}\hat {\sigma }_{ - }^{{\left( k \right)}}$ | |
| 2-й спин-орбитальный | 16, 17 k = 1, 2 | σ– | q2σ | ${{q}_{ + }}{{q}_{ - }}\hat {\sigma }_{z}^{{\left( k \right)}}$ |
| 18, 19 k = 1, 2 | π | q2σ | ${{q}_{ + }}{{q}_{ - }}\hat {\sigma }_{ + }^{{\left( k \right)}},\,\,{{q}_{ + }}{{q}_{ - }}\hat {\sigma }_{ - }^{{\left( k \right)}}$ | |
| 20, 21 k = 1, 2 | π | q2σ | $q_{ + }^{2}\hat {\sigma }_{ - }^{{\left( k \right)}},~\,\,q_{ - }^{2}\hat {\sigma }_{ + }^{{\left( k \right)}}~$ | |
| 22, 23 k = 1, 2 | δ | q2σ | $q_{ + }^{2}\hat {\sigma }_{z}^{{\left( k \right)}},\,\, - q_{ - }^{2}\hat {\sigma }_{z}^{{\left( k \right)}}$ | |
| 24, 25 k = 1, 2 | ϕ | q2σ | $q_{ + }^{2}\hat {\sigma }_{ + }^{{\left( k \right)}},\,\,q_{ - }^{2}\hat {\sigma }_{ - }^{{\left( k \right)}}$ |
где
(9)
${{\hat {h}}_{0}} = \sum\limits_{k = 1,~2} {\left[ {{}_{{}}^{k}{{{\hat {h}}}_{ + }}\left( {{{\pi }_{ - }}} \right)\hat {\sigma }_{ + }^{{\left( k \right)}} + {}_{{}}^{k}{{{\hat {h}}}_{ - }}\left( {{{\pi }_{ + }}} \right)\hat {\sigma }_{ - }^{{\left( k \right)}} + {}_{{}}^{k}{{{\hat {h}}}_{z}}\left( {{{\sigma }^{ - }}} \right)\hat {\sigma }_{z}^{{\left( k \right)}}} \right]} {\kern 1pt} ,$(10)
$\begin{gathered} {{{\hat {h}}}_{1}} = \sum\limits_{k = 1,2} {\left[ {{}_{~}^{k}\hat {h}_{ + }^{ + }} \right.\left( {{{\delta }_{ - }}} \right){{q}_{ + }}\hat {\sigma }_{ + }^{{\left( k \right)}} + {}_{~}^{k}\hat {h}_{ - }^{ - }\left( {{{\delta }_{ + }}} \right){{q}_{ - }}\hat {\sigma }_{ - }^{{\left( k \right)}} + {}_{~}^{k}{{{\hat {h}}}^{ + }}\left( {{{\sigma }^{ + }}} \right)\left( {{{q}_{ - }}\hat {\sigma }_{ + }^{{\left( k \right)}} + {{q}_{ + }}\hat {\sigma }_{ - }^{{\left( k \right)}}} \right) + } \\ \left. { + \,\,{}_{~}^{k}{{{\hat {h}}}^{ - }}\left( {{{\sigma }^{ - }}} \right)\left( {{{q}_{ - }}\hat {\sigma }_{ + }^{{\left( k \right)}} - {{q}_{ + }}\hat {\sigma }_{ - }^{{\left( k \right)}}} \right) + \,~{}_{~}^{k}\hat {h}_{z}^{ + }\left( {{{\pi }_{ - }}} \right){{q}_{ + }}\hat {\sigma }_{z}^{{\left( k \right)}} - {}_{~}^{k}\hat {h}_{z}^{ - }\left( {{{\pi }_{ + }}} \right){{q}_{ - }}\hat {\sigma }_{z}^{{\left( k \right)}}} \right]~, \\ \end{gathered} $(11)
$\begin{gathered} {{{\hat {h}}}_{2}} = \sum\limits_{k = 1,2} {\left\{ {\left[ {{}_{~}^{k}\hat {h}_{ + }^{{ + + }}\left( {{{{\Phi }}_{ - }}} \right)q_{ + }^{2} + {}_{~}^{k}\hat {h}_{ + }^{{ - - }}\left( {{{{\pi }}_{ + }}} \right)q_{ - }^{2} + {}_{~}^{k}\hat {h}_{ + }^{{ + - }}\left( {{{{\pi }}_{ - }}} \right){{q}_{ + }}{{q}_{ - }}} \right]\hat {\sigma }_{ + }^{{\left( k \right)}}} \right. + } \\ + \,\,\left[ {{}_{~}^{k}\hat {h}_{ - }^{{ + + }}\left( {{{{\pi }}_{ - }}} \right)q_{ + }^{2} + {}_{~}^{k}\hat {h}_{ - }^{{ - - }}\left( {{{{\Phi }}_{ + }}} \right)q_{ - }^{2} + {}_{~}^{k}\hat {h}_{ - }^{ \pm }\left( {{{{\pi }}_{ + }}} \right){{q}_{ + }}{{q}_{ - }}} \right]\hat {\sigma }_{ - }^{{\left( k \right)}} + \\ + \,\,\left[ {{}_{~}^{k}\hat {h}_{z}^{{ + + }}\left( {{{{\delta }}_{ - }}} \right)q_{ + }^{2} - {}_{~}^{k}\hat {h}_{z}^{{ - - }}\left( {{{{\delta }}_{ + }}} \right)q_{ - }^{2} + {}_{~}^{k}\hat {h}_{z}^{{ + - }}\left( {{{\sigma }^{ - }}} \right){{q}_{ + }}{{q}_{ - }}} \right]\left. {\hat {\sigma }_{z}^{{\left( k \right)}}} \right\}. \\ \end{gathered} $Каждый операторный коэффициент рядов Тейлора (5)–(11) преобразуется по неприводимому представлению и его строчке, указанных в качестве аргумента этого оператора. Подчеркнем, что все операторные коэффициенты рядов Тейлора (5)–(11) преобразуются по неприводимым представлениям, которые комплексно сопряжены неприводимым представлениям соответствующих симметризованных комбинаций. Данная симметрия операторных коэффициентов обеспечивает инвариантность в группе C∞v операторов ${{\hat {H}}_{i}}$ (i = 1, 2) и ${{\hat {h}}_{j}}$ (j = 0, 1, 2).
ДИАБАТИЧЕСКИЙ БАЗИС ЭЛЕКТРОННЫХ СОСТОЯНИЙ
Ниже мы используем цилиндрические координаты, в которых ось z совпадает с осью симметрии линейной молекулы, r – цилиндрический радиус и φ – угол поворота вокруг оси z. Введем далее две электронные молекулярные орбитали с симметрией Σ+ –
(12)
$\begin{gathered} Q\left( k \right) = Q\left( {{{r}_{k}},{{z}_{k}}} \right), \\ S\left( k \right) = S\left( {{{r}_{k}},{{z}_{k}}} \right),\,\,\,\,~k = 1,2, \\ \end{gathered} $и две молекулярные орбитали с симметрией Π –
(13)
$P\left( k \right){{e}^{{ \pm i{{\varphi }_{k}}}}} = P\left( {{{r}_{k}},{{z}_{k}}} \right){{e}^{{i{{\varphi }_{k}}}}},\,\,\,\,~k = 1,2.$С использованием введенных молекулярных орбиталей мы можем сконструировать следующие двухэлектронные диабатические состояния с симметриями 3Π и 3Σ+:
(14)
$\begin{gathered} {{\psi }_{{ + 2}}} = \frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left[ {P\left( 1 \right)S\left( 2 \right){{e}^{{i{{\varphi }_{1}}}}} - P\left( 2 \right)S\left( 1 \right){{e}^{{i{{\varphi }_{2}}}}}} \right]{{\alpha }_{1}}{{\alpha }_{2}}, \\ {{\psi }_{{ + 1}}} = \frac{1}{2}\left[ {P\left( 1 \right)S\left( 2 \right){{e}^{{i{{\varphi }_{1}}}}} - P\left( 2 \right)S\left( 1 \right){{e}^{{i{{\varphi }_{2}}}}}} \right]\left( {{{\alpha }_{1}}{{\beta }_{2}} + {{\alpha }_{2}}{{\beta }_{1}}} \right), \\ {{\psi }^{{ + 1}}} = ~\frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left[ {Q\left( 1 \right)S\left( 2 \right) - Q\left( 2 \right)S\left( 1 \right)} \right]{{\alpha }_{1}}{{\alpha }_{2}}, \\ {{\psi }_{0}} = \frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left[ {P\left( 1 \right)S\left( 2 \right){{e}^{{i{{\varphi }_{1}}}}} - P\left( 2 \right)S\left( 1 \right){{e}^{{i{{\varphi }_{2}}}}}} \right]{{\beta }_{1}}{{\beta }_{2}}, \\ {{\psi }^{0}} = \frac{1}{2}\left[ {Q\left( 1 \right)S\left( 2 \right) - Q\left( 2 \right)S\left( 1 \right)} \right]\left( {{{\alpha }_{1}}{{\beta }_{2}} + {{\alpha }_{2}}{{\beta }_{1}}} \right), \\ {{{\tilde {\psi }}}_{0}} = \frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left[ {P\left( 1 \right)S\left( 2 \right){{e}^{{ - i{{\varphi }_{1}}}}} - P\left( 2 \right)S\left( 1 \right){{e}^{{ - i{{\varphi }_{2}}}}}} \right]{{\alpha }_{1}}{{\alpha }_{2}}, \\ {{\psi }^{{ - 1}}} = \frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left[ {Q\left( 1 \right)S\left( 2 \right) - Q\left( 2 \right)S\left( 1 \right)} \right]{{\beta }_{1}}{{\beta }_{2}}, \\ {{\psi }_{{ - 1}}} = \frac{1}{2}\left[ {P\left( 1 \right)S\left( 2 \right){{e}^{{ - i{{\varphi }_{1}}}}} - P\left( 2 \right)S\left( 1 \right){{e}^{{ - i{{\varphi }_{2}}}}}} \right]\left( {{{\alpha }_{1}}{{\beta }_{2}} + {{\alpha }_{2}}{{\beta }_{1}}} \right), \\ {{\psi }_{{ - 2}}} = \frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left[ {P\left( 1 \right)S\left( 2 \right){{e}^{{ - i{{\varphi }_{1}}}}} - P\left( 2 \right)S\left( 1 \right){{e}^{{ - i{{\varphi }_{2}}}}}} \right]{{\beta }_{1}}{{\beta }_{2}}~. \\ \end{gathered} $Введенные диабатические электронные базисные состояния характеризуются следующими типами симметрии:
где нижними индексами в правых частях обозначена суммарная проекция углового момента (jz = = lz + sz) на молекулярную ось z.
Отметим, что введенные молекулярные орбитали (12) и (13) позволяют “сконструировать” еще шесть диабатических состояний типа $^{3}{{\prod }_{{ \pm 2}}},$ $^{3}{{\prod }_{{ \pm 1}}},$ ${{2}^{3}}{{\prod }_{0}},$ в которых вместо Σ+-орбитали S фигурирует Σ+-орбиталь Q. Мы, однако, не включаем эти состояния в базис, полагая, что они существенно выше по энергии, чем базисные состояния (14). В представлении диабатического электронного базиса (14) оператор обращения времени (4) приобретает следующий вид:
(15)
$\hat {T} = \left| {\begin{array}{*{20}{c}} {}&{}&{}&{}&{}&{}&{}&{}&{ - 1} \\ {}&{}&{}&{}&{}&{}&{}&1&{} \\ {}&{}&{}&{}&{}&{}&{ - 1}&{}&{} \\ {}&{}&{}&{}&{}&{ - 1}&{}&{}&{} \\ {}&{}&{}&{}&1&{}&{}&{}&{} \\ {}&{}&{}&{ - 1}&{}&{}&{}&{}&{} \\ {}&{}&{ - 1}&{}&{}&{}&{}&{}&{} \\ {}&1&{}&{}&{}&{}&{}&{}&{} \\ { - 1}&{}&{}&{}&{}&{}&{}&{}&{} \end{array}} \right|~\widehat {{\text{c}}{\text{.c}}{\text{.}}}\,,$Мы приводим здесь также вид вибронных операторов симметрии [8] – операторов, с которыми вибронная матрица электронного гамильтониана должна коммутировать, как и с оператором $\hat {T}{\text{:}}$
(16)
$\hat {G}_{z}^{{{v}ib}}\left( \varepsilon \right) = \left| {\begin{array}{*{20}{c}} {{{e}^{{2i\varepsilon }}}}&{}&{}&{}&{}&{}&{}&{}&{} \\ {}&{{{e}^{{i\varepsilon }}}}&{}&{}&{}&{}&{}&{}&{} \\ {}&{}&{{{e}^{{i\varepsilon }}}}&{}&{}&{}&{}&{}&{} \\ {}&{}&{}&1&{}&{}&{}&{}&{} \\ {}&{}&{}&{}&1&{}&{}&{}&{} \\ {}&{}&{}&{}&{}&1&{}&{}&{} \\ {}&{}&{}&{}&{}&{}&{{{e}^{{ - i\varepsilon }}}}&{}&{} \\ {}&{}&{}&{}&{}&{}&{}&{{{e}^{{ - i\varepsilon }}}}&{} \\ {}&{}&{}&{}&{}&{}&{}&{}&{{{e}^{{ - 2i\varepsilon }}}} \end{array}} \right|{{\hat {C}}_{q}}\left( \varepsilon \right),$(17)
$\hat {Z}_{\sigma }^{{{v}ib}} = \left| {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{}&{} \\ {}&{}&{} \\ {}&{}&{} \end{array}}&{\begin{array}{*{20}{c}} {}&{}&{} \\ {}&{}&{} \\ {}&{}&{} \end{array}}&{\begin{array}{*{20}{c}} {}&{}&1 \\ {}&{ - 1}&{} \\ 1&{}&{} \end{array}} \\ {\begin{array}{*{20}{c}} {}&{}&{} \\ {}&{}&{} \\ {}&{}&{} \end{array}}&{\begin{array}{*{20}{c}} {}&{}&1 \\ {}&{ - 1}&{} \\ 1&{}&{} \end{array}}&{\begin{array}{*{20}{c}} {}&{}&{} \\ {}&{}&{} \\ {}&{}&{} \end{array}} \\ {\begin{array}{*{20}{c}} {}&{}&1 \\ {}&{ - 1}&{} \\ 1&{}&{} \end{array}}&{\begin{array}{*{20}{c}} {}&{}&{} \\ {}&{}&{} \\ {}&{}&{} \end{array}}&{\begin{array}{*{20}{c}} {}&{}&{} \\ {}&{}&{} \\ {}&{}&{} \end{array}} \end{array}} \right|{{\hat {\sigma }}_{q}}{\kern 1pt} ,$где операторы ${{\hat {C}}_{q}}(\varepsilon )$ и ${{\hat {\sigma }}_{q}}$ действуют на π-моды согласно следующим соотношениям:
Матричные факторы операторов симметрии (15)–(17) являются операторами симметрии (4), (2), (3) гамильтониана линейной молекулы в представлении диабатического электронного базиса (14). Вибронные операторы симметрии (16), (17) являются математическим выражением того факта, что электронный гамильтониан деформированной молекулы (вибронная матрица) инвариантен по отношению к одновременным преобразованиям симметрии электронных переменных и нормальных мод [9].
ЭЛЕКТРОСТАТИЧЕСКАЯ (НЕРЕЛЯТИВИСТСКАЯ) ЧАСТЬ ВИБРОННОЙ МАТРИЦЫ
В этом разделе мы найдем матричное представление электростатического гамильтониана (5)–(7) в базисе электронных состояний (14). Учитывая тот факт, что электростатический гамильтониан не действует на спиновые состояния базисных функций и потому не смешивает их, отличные от нуля матричные элементы возникают только между базисными функциями с одинаковыми спиновыми состояниями.
Отличные от нуля недиагональные матричные элементы описывают два типа эффектов: квадратичное (реннеровское) вибронное взаимодействие орбитальных компонент Π-состояний и линейное вибронное взаимодействие орбитальных компонент Π-состояний с Σ+-состояниями. В результате вычислений получаем следующую электростатическую часть вибронной матрицы 9 × 9:
(18)
$\begin{gathered} {{{\hat {H}}}_{{es}}} = ({}_{~}^{3}{{{\Pi }}_{e}} + {{c}_{1}}{{\rho }^{2}})~{\text{diag}}\left( {1,1,0,1,0,1,0,1,1} \right) + ({}_{~}^{3}{\Sigma }_{e}^{ + } + {{c}_{0}}{{\rho }^{2}})~{\text{diag}}\left( {0,0,1,0,1,0,1,0,0} \right) + \\ + \,\,\left| {\begin{array}{*{20}{c}} {}&{}&{b{{q}_{ - }}}&{}&{}&{aq_{ - }^{2}}&{}&{}&{} \\ {}&{}&{}&{}&{b{{q}_{ - }}}&{}&{}&{aq_{ - }^{2}}&{} \\ {bq_{ + }^{{}}}&{}&{}&{}&{}&{}&{}&{}&{} \\ {}&{}&{}&{}&{}&{}&{b{{q}_{ - }}}&{}&{aq_{ - }^{2}{\kern 1pt} } \\ {}&{bq_{ + }^{{}}}&{}&{}&{}&{}&{}&{b{{q}_{ - }}}&{} \\ {aq_{ + }^{2}}&{}&{}&{}&{}&{}&{}&{}&{} \\ {}&{}&{}&{bq_{ + }^{{}}}&{}&{}&{}&{}&{b{{q}_{ - }}} \\ {}&{aq_{ + }^{2}}&{}&{}&{b{{q}_{ + }}}&{}&{}&{}&{} \\ {}&{}&{}&{aq_{ + }^{2}}&{}&{}&{b{{q}_{ + }}}&{}&{} \end{array}} \right|\begin{array}{*{20}{c}} {\psi _{{ + 2}}^{{}}} \\ {\psi _{{ + 1}}^{{}}} \\ {\psi _{{}}^{{ + 1}}} \\ \begin{gathered} \psi _{0}^{{}} \hfill \\ \psi _{{}}^{0} \hfill \\ \tilde {\psi }_{0}^{{}} \hfill \\ \psi _{{}}^{{ - 1}} \hfill \\ \psi _{{ - 1}}^{{}} \hfill \\ \psi _{{ - 2}}^{{}} \hfill \\ \end{gathered} \end{array}{\text{,}} \\ \begin{array}{*{20}{c}} {{{\psi }_{{ + 2}}}}&{{{\psi }_{{ + 1}}}}&{{{\psi }^{{ + 1}}}}&{{{\psi }_{0}}}&{{{\psi }^{0}}}&{{{{\tilde {\psi }}}_{0}}}&{{{\psi }^{{ - 1}}}}&{{{\psi }_{{ - 1}}}}&{{{\psi }_{{ - 2}}}} \end{array} \\ \end{gathered} $где q± = pe±ix и a, b, c0, c1, $^{3}{{\prod }_{e}},$ $^{3}\sum _{e}^{ + }$ – вещественные постоянные. В гамильтониане (18) символами $^{3}{{\prod }_{e}}$ и $^{3}\sum _{e}^{ + }$ обозначены энергии электронных состояний $^{3}\prod $ и $^{3}\sum _{{}}^{ + }$ линейной трехатомной молекулы.
СПИН-ОРБИТАЛЬНАЯ ЧАСТЬ ВИБРОННОЙ МАТРИЦЫ
Вычисляя матричные элементы оператора постоянных спинорбитальных вкладов ${{\hat {h}}_{0}}$ (см. (9)), мы прежде всего учитываем правила отбора в группе C∞v по проекции полного углового момента (jz = lz + sz) на молекулярную ось симметрии z; а именно, отличные от нуля матричные элементы ${{\hat {h}}_{0}}$ соответствуют базисным функциям с одинаковой проекцией полного углового момента на ось z. Эти правила отбора позволяют получить эрмитову 9 × 9-матрицу ${{\hat {h}}_{0}},$ содержащую четыре комплексных постоянных. Дальнейшее применение к этой матрице требований коммутации с операторами симметрии (15)–(17) сокращает число постоянных до двух вещественных параметров. В итоге мы получаем следующее матричное представление ${{\hat {h}}_{0}}{\text{:}}$
(19)
$\begin{gathered} {{{\hat {h}}}_{0}} = \\ = \left| {\begin{array}{*{20}{c}} {}&{}&{}&{}&{}&{}&{}&{}&{} \\ {}&{}&\alpha &{}&{}&{}&{}&{}&{} \\ {}&\alpha &{}&{}&{}&{}&{}&{}&{} \\ {}&{}&{}&{}&{\beta _{{}}^{{}}}&{}&{}&{}&{} \\ {}&{}&{}&\beta &{}&{ - \beta \,\,}&{}&{}&{} \\ {}&{}&{}&{}&{ - \beta }&{}&{}&{}&{} \\ {}&{}&{}&{}&{}&{}&{}&{ - \alpha }&{\,\,\,\,\,\,{\kern 1pt} {\kern 1pt} } \\ {}&{}&{}&{}&{}&{}&{ - \alpha }&{}&{} \\ {}&{}&{}&{}&{}&{}&{}&{}&{} \end{array}} \right|\begin{array}{*{20}{c}} {{{\psi }_{{ + 2}}}} \\ {{{\psi }_{{ + 1}}}} \\ {{{\psi }^{{ + 1}}}} \\ {\psi {{{_{0}^{{}}}}_{{}}}} \\ {{{\psi }^{0}}} \\ {{{{\tilde {\psi }}}_{0}}} \\ {{{\psi }^{{ - 1}}}} \\ {{{\psi }_{{ - 1}}}} \\ {{{\psi }_{{ - 2}}}} \end{array}{\text{,}} \\ \begin{array}{*{20}{c}} {{{\psi }_{{ + 2}}}{\kern 1pt} }&{{{\psi }_{{ + 1}}}}&{{{\psi }^{{ + 1}}}}&{{{\psi }_{0}}}&{{{\psi }^{0}}}&{{{{\tilde {\psi }}}_{0}}}&{{{\psi }^{{ - 1}}}}&{{{\psi }_{{ - 1}}}}&{{{\psi }_{{ - 2}}}} \end{array} \\ \end{gathered} $где α, β – вещественные спин-орбитальные параметры.
При вычислении матрицы ${{\hat {h}}_{1}}$ отличными от нуля будут матричные элементы между базисными функциями с разницей проекции полного углового момента на ось z, равной единице. Эти правила отбора в группе C∞v позволяют получить эрмитову матрицу 9 × 9, зависящую от q+, q– и содержащую 16 комплексных параметров. Требования коммутации этой матрицы с операторами симметрии (15)–(17) сокращают число независимых параметров до восьми вещественных постоянных. В результате мы приходим к матрице ${{\hat {h}}_{1}}$ следующего вида:
(20)
${{\hat {h}}_{1}} = \left| {\begin{array}{*{20}{c}} {}&{{{\gamma }_{1}}{{q}_{ - }}}&{{{\gamma }_{2}}{{q}_{ - }}}&{}&{}&{}&{}&{}&{} \\ {{{\gamma }_{1}}{{q}_{ + }}}&{}&{}&{{{\gamma }_{3}}{{q}_{ - }}}&{{{\gamma }_{4}}{{q}_{ - }}}&{{{\gamma }_{5}}{{q}_{ - }}}&{}&{}&{} \\ {{{\gamma }_{2}}{{q}_{ + }}}&{}&{}&{{{\gamma }_{6}}{{q}_{ - }}}&{{{\gamma }_{7}}{{q}_{ - }}}&{{{\gamma }_{8}}{{q}_{ - }}}&{}&{}&{} \\ {}&{{{\gamma }_{3}}{{q}_{ + }}}&{{{\gamma }_{6}}{{q}_{ + }}}&{}&{}&{}&{{{\gamma }_{8}}{{q}_{ - }}}&{ - {{\gamma }_{5}}{{q}_{ - }}}&{} \\ {}&{{{\gamma }_{4}}{{q}_{ + }}}&{{{\gamma }_{7}}{{q}_{ + }}}&{}&{}&{}&{ - {{\gamma }_{7}}{{q}_{ - }}}&{{{\gamma }_{4}}{{q}_{ - }}}&{} \\ {}&{{{\gamma }_{5}}{{q}_{ + }}}&{{{\gamma }_{8}}{{q}_{ + }}}&{}&{}&{}&{{{\gamma }_{6}}{{q}_{ - }}}&{ - {{\gamma }_{3}}{{q}_{ - }}}&{} \\ {}&{}&{}&{{{\gamma }_{8}}{{q}_{ + }}}&{ - {{\gamma }_{7}}{{q}_{ + }}}&{{{\gamma }_{6}}{{q}_{ + }}}&{}&{}&{ - {{\gamma }_{2}}{{q}_{ - }}} \\ {}&{}&{}&{ - {{\gamma }_{5}}{{q}_{ + }}}&{{{\gamma }_{4}}{{q}_{ + }}}&{ - {{\gamma }_{3}}{{q}_{ + }}}&{}&{}&{ - {{\gamma }_{1}}{{q}_{ - }}} \\ {}&{}&{}&{}&{}&{}&{{{\gamma }_{2}}{{q}_{ + }}}&{ - {{\gamma }_{1}}{{q}_{ + }}}&{_{{}}^{{}}} \end{array}} \right|\begin{array}{*{20}{c}} {{{\psi }_{{ + 2}}}} \\ {{{\psi }_{{ + 1}}}} \\ {{{\psi }^{{ + 1}}}} \\ {{{\psi }_{0}}} \\ {{{\psi }^{0}}} \\ {{{{\tilde {\psi }}}_{0}}} \\ {{{\psi }^{{ - 1}}}} \\ {{{\psi }_{{ - 1}}}} \\ {{{\psi }_{{ - 2}}}_{{}}^{{}}} \end{array},$где γk (k = 1, …, 8) – вещественные спин-орбитальные параметры.
Расчет матрицы ${{\hat {h}}_{2}}$ аналогичен расчетам ${{\hat {h}}_{0}}$ и ${{\hat {h}}_{1}}.$ Отличные от нуля матричные элементы ${{\hat {h}}_{2}}$ соответствуют базисным функциям с разницей проекции полного углового момента на ось z, равной двум. Это правило отбора по проекции полного углового момента позволяет получить ${{\hat {h}}_{2}}$ в виде эрмитовой матрицы 9 × 9, содержащей десять комплексных параметров. Требования коммутации этой матрицы с операторами обращения времени (15), поворота (16) и отражения (17) сокращают число параметров до шести вещественных постоянных. В результате получаем следующее матричное представление оператора квадратичных вкладов ${{\hat {h}}_{2}}{\text{:}}$
(21)
$\begin{gathered} {{{\hat {h}}}_{2}} = \,\,\left| {\begin{array}{*{20}{c}} {}&{}&{}&{{{\delta }_{1}}q_{ - }^{2}}&{{{\delta }_{2}}q_{ - }^{2}}&{{{\delta }_{3}}q_{ - }^{2}}&{}&{}&{} \\ {}&{}&{}&{}&{}&{}&{{{\delta }_{4}}q_{ - }^{2}}&{{{\delta }_{5}}q_{ - }^{2}}&{} \\ {}&{}&{}&{}&{}&{}&{{{\delta }_{6}}q_{ - }^{2}}&{ - {{\delta }_{4}}q_{ - }^{2}}&{} \\ {{{\delta }_{1}}q_{ + }^{2}}&{}&{}&{}&{}&{}&{}&{}&{{{\delta }_{3}}q_{ - }^{2}} \\ {{{\delta }_{2}}q_{ + }^{2}}&{}&{}&{}&{}&{}&{}&{}&{ - {{\delta }_{2}}q_{ - }^{2}} \\ {{{\delta }_{3}}q_{ + }^{2}}&{}&{}&{}&{}&{}&{}&{}&{{{\delta }_{1}}q_{ - }^{2}} \\ {}&{{{\delta }_{4}}q_{ + }^{2}}&{{{\delta }_{6}}q_{ + }^{2}}&{}&{}&{}&{}&{}&{} \\ {}&{{{\delta }_{5}}q_{ + }^{2}}&{ - {{\delta }_{4}}q_{ + }^{2}}&{}&{}&{}&{}&{}&{} \\ {}&{}&{}&{{{\delta }_{3}}q_{ + }^{2}}&{ - {{\delta }_{2}}q_{ + }^{2}}&{{{\delta }_{1}}q_{ + }^{2}}&{}&{}&{} \end{array}} \right|\begin{array}{*{20}{c}} {\psi _{{ + 2}}^{{}}} \\ {\psi _{{ + 1}}^{{}}} \\ {\psi _{{}}^{{ + 1}}} \\ \begin{gathered} \psi _{0}^{{}} \hfill \\ \psi _{{}}^{0} \hfill \\ \tilde {\psi }_{0}^{{}} \hfill \\ \psi _{{}}^{{ - 1}} \hfill \\ \psi _{{ - 1}}^{{}} \hfill \\ \psi _{{ - 2}}^{{}} \hfill \\ \end{gathered} \end{array}{\text{,}} \\ \begin{array}{*{20}{l}} {{{\psi }_{{ + 2}}}\,\,}&{{{\psi }_{{ + 1}}}}&{{{\psi }^{{ + 1}}}\,\,\,}&{{{\psi }_{0}}\,\,}&{{{\psi }^{0}}\,\,}&{{{{\tilde {\psi }}}_{0}}\,}&{{{\psi }^{{ - 1}}}\,\,}&{{{\psi }_{{ - 1}}}\,\,}&{\psi _{{ - 2}}^{{}}\,\,} \end{array} \\ \end{gathered} $где δk (k = 1, …, 6) – вещественные спин-орбитальные параметры.
ПОЛНАЯ ВИБРОННАЯ МАТРИЦА. ПОВЕРХНОСТИ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
Полная вибронная матрица релятивистского псевдо-эффекта Реннера (3Π + 3Σ+) × π является суммой четырех составляющих матриц (18)–(21). Полная вибронная матрица включает в себя шесть электростатических и 16 спин-орбитальных вещественных постоянных параметров и имеет весьма сложную структуру. Детальный вид этой матрицы представлен на рис. 1.
Поверхности потенциальной энергии (ППЭ) являются собственными значениями вибронной матрицы $\hat {H}$ (см. табл. 2 ). В силу свойств симметрии вибронной матрицы (15)–(17) ППЭ являются инвариантами группы симметрии С∞v и в рассматриваемом случае зависят только от ρ (т.е. являются аксиально-симметричными над плоскостью нормальных π-мод (qx, qy)). Сложная структура эрмитовой вибронной 9 × 9-матрицы $\hat {H}$ не позволяет получить аналитические выражения для потенциальных поверхностей. На рис. 2 представлены зависимости ППЭ от ρ для некоторого частного набора параметров. С учетом того, что вибронная матрица $\hat {H}$ включает в себя 22 постоянных вещественных параметра, зависимости ППЭ от ρ могут быть самыми различными даже при условии, что спин-орбитальные константы, как правило, в несколько раз меньше электростатических (той же размерности).
Рис. 2.
Зависимости ППЭ от ρ для частного набора параметров. Симметрии электронных состояний: U1, U2, U5, U8, U9$ \in $ A", U3, U4, U6, U7$ \in $ A'. Параметры вибронной матрицы $\hat {H},$ использованные при расчете потенциальных поверхностей: энергетические постоянные (эВ) – $^{3}\sum _{e}^{ + }$ = 0, $^{3}{{\prod }_{e}}$ = 1.0, α = 1.5, β = 1.2; силовые постоянные (эВ/Å) – b = 3.0, γ1 = 0.8, γ2 = –0.7, γ3 = 0.6, γ4 = –0.6, γ5 = 0.5, γ6 = –0.5, γ7 = 0.4, γ8 = 0.2; частотные постоянные (эВ/Å2) – c0 = 0.8, c1 = 0.6, a = 0.4, δ1 = 0.2, δ2 = –0.15, δ3 = 0.15, δ4 = –0.12, δ5 = 0.1, δ6 = –0.1.
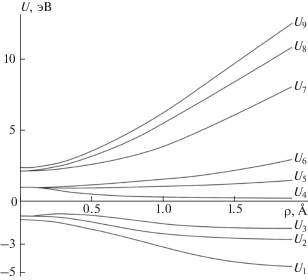
При q± ≠ 0 молекулярной группой симметрии является группа Cs, содержащая тождественную операцию и отражение в плоскости изогнутой молекулы и характеризующаяся неприводимыми представлениями A' и A". В силу этого девяти потенциальным поверхностям, представленным на рис. 2, соответствуют электронные состояния A'- и A"-симметрии. Детальный анализ собственных векторов вибронной матрицы $\hat {H}$ (см. рис. 1) позволяет заключить, что пять из девяти электронных состояний изогнутой молекулы (1, 2, 5, 8, 9) имеют симметрию A " и четыре состояния (3, 4, 6, 7) – симметрию A', как показано на рис. 2.
Следует подчеркнуть, что числа состояний A'- и A "-симметрии не зависят от численных значений параметров, выбранных для иллюстрации потенциальных поверхностей, и определяются свойствами симметрии диабатических базисных состояний (14). От численных значений параметров вибронной матрицы зависит, однако, порядок следования (по энергии) электронных состояний A'- и A"-симметрии.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Как следует из рис. 1, при ρ = 0 имеется пять различных энергетических уровней: один трехкратно вырожденный уровень, два двукратных и два простых уровня. Вибронная матрица $\hat {H},$ представленная на рис. 1, позволяет найти аналитический вид этих уровней линейной молекулы, выразив их через энергетические параметры. В частности, имеется трехкратно вырожденный уровень –
пара двукратно вырожденных уровней –
и пара простых уровней –
При деформации молекулы π-модами зависимости этих девяти потенциальных поверхностей от ρ определяются девятью силовыми и девятью частотными параметрами. Каких-либо общих закономерностей для этих зависимостей сформулировать невозможно. При ρ ≠ 0 все поверхности потенциальной энергии, как правило, невырождены. Следует, однако, допустить возможность пересечения потенциальных поверхностей электронных состояний различной симметрии (A' и A ") и квазипересечений для состояний одинаковой симметрии. Для каждой молекулярной системы форма потенциальных поверхностей U1(ρ), …, U9(ρ) будет специфической.
Рассчитанная в работе вибронная 9 × 9-матрица $\hat {H}$ описывает релятивистский псевдо-эффект Реннера (3Π + 3Σ+) × π в линейных трехатомных молекулах с чётным числом электронов и имеющих в электронном спектре два соседних состояний 3Π и 3Σ+. Энергетические, силовые и частотные параметры вибронной матрицы могут быть определены по ab initio точкам потенциальных поверхностей, рассчитанных с учетом спин-орбитального взаимодействия [10].
Полученные в работе результаты применимы для линейных молекул, структурно подобных молекулам HCN и COS [11], в которых составляющие атомы замещены более тяжелыми, но с эквивалентными химическими свойствами (т.е. с похожим строением внешних электронных оболочек).
ЗАКЛЮЧЕНИЕ
Таким образом отметим, что расчет вибронной матрицы в базисе (14), но с более высокой точностью (с включением третьих и четвертых степеней π-мод) позволил бы дополнительно получить несколько ненулевых матричных элементов вида
где dτ означает интегрирование по пространственным и спиновым переменным двух электронов. При этом аналогично с (22) расположенные матричные элементы будут пропорциональны тем же степеням q+.
Авторы выражают благодарность доктору физико-математических наук В.Г. Ушакову за плодотворные дискуссии по теме данной работы.
Работа выполнена в рамках госзаданий (регистрационные номера 012 013 618 60 и 0089-2019-0017).
Список литературы
Köppel H., Domcke D., Cederbaum L.S. // J. Chem. Phys. 1981. V. 74. № 5. P. 2945.
Банкер Ф. Симметрия молекул и молекулярная спектроскопия. М.: Мир, 1981.
Mishra S., Poluyanov L.V., Domcke W. // J. Chem. Phys. 2007. V. 126. 134312.
Poluyanov L.V., Domcke W. // Adv. Ser. Phys. Chem. 2011. V. 17. P. 117.
Mishra S., Poluyanov L.V., Domcke W. // Chem. Phys. Lett. 2007. V. 446. P. 256.
Poluyanov L.V., Domcke W. // Springer Ser. Chem. Phys. 2009. V. 97. P. 77.
Вигнер Е. Теория групп. М.: Изд-во иностр. лит., 1961.
Poluyanov L.V., Domcke W. // J. Chem. Phys. 2012. V. 137. 114101.
Ландау Л.Д., Лифшиц Е.М. Квантовая механика. М.: Наука, 1974.
Dyall K.G., Faegry K. Inroduction to relativistic quantum chemistry. Oxford University Press, 2007.
Герцберг Г. Электронные спектры и строение многоатомных молекул. М.: Мир, 1969.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика