Химическая физика, 2020, T. 39, № 4, стр. 68-72

Моделирование термосферного эффекта волны цунами в многослойной атмосфере

С. Б. Лебле^1, *, Е. С. Смирнова¹

¹ Балтийский федеральный университет им. И. Канта
Калининград, Россия

Поступила в редакцию 18.02.2019
После доработки 13.05.2019
Принята к публикации 20.05.2019

DOI: 10.31857/S0207401X20040123

Аннотация

Задача распространения граничного режима акустической волны используется для моделирования эффекта возмущения атмосферного газа. Атмосфера приближенно описывается как одномерная многослойная с экспоненциальной структурой по плотности в каждом слое. На границах слоев и на границе вода–воздух определяется граничный режим, фиксирующий направление распространения. Связь между атмосферными параметрами (давлением, плотностью и скоростью) находится с помощью операторов проектирования на подпространства оператора z-эволюции для каждого слоя. В результате получаем спектральный состав акустического возмущения атмосферы на произвольной высоте, включая ионосферные высоты, что может использоваться для расчета ионосферного эффекта.

Ключевые слова: акустика, атмосфера, многослойная модель, цунами.

1. ВВЕДЕНИЕ

Проблема распространения длинных акустических волн в атмосфере имеет значительную историю. Пока длина волны много меньше основного параметра неоднородности невозмущенного газа – так называемой высоты однородной атмосферы (H), можно пользоваться приближенным описанием. Такое описание, по сути, позволяет использовать понятия однородной среды распространения, рассматривая H как параметр или, учитывая слабую неоднородность, применяя методы, подобные квазиклассическому приближению квантовой механики [11 ] . Если же спектр длин волн существенно захватывает величины порядка H, приходится прибегать к разбиению атмосферы на горизонтальные слои, считая стратификацию в ней экспоненциальной [2].

Для экспоненциальной атмосферы, которую часто используют не только как модель, но и как источник терминологии при описании атмосферных волн, получены важные результаты как для линейной теории [3], так и для нелинейного обобщения в различных порядках по степени нелинейности [4]. Так, выведены дисперсионные соотношения, которые и дают основу для вводимых понятий и практических рекомендаций для геофизики. При этом в основном рассматривалась задача Коши с подходящим набором начальных условий.

В нашей работе рассматривается задача о распространении граничного режима; при этом генерирующий режим задается на поверхности раздела вода–воздух. По традиции мы разделяем атмосферу на слои с постоянным H [2]. Такая задача может быть интересна для моделирования высотного эффекта поверхностных волн в океане. Особенно это важно для таких волн, как цунами, обладающих большими амплитудой и масштабом [5]. Опираясь на большой горизонтальный масштаб рассматриваемых поверхностных волн, мы пользуемся одномерной моделью атмосферы, проектируя общее решение задачи о распространении граничного режима на подпространство однонаправленных волн. Результаты представлены в виде спектрального распределения амплитуд на границах слоев сшивания.

2. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ

2.1. Основные уравнения

Рассмотрим задачу распространения акустических волн в экспоненциально стратифицированной атмосфере. Давление и плотность невозмущенной атмосферы описываются законом

$\begin{gathered} \bar {p}\left( z \right) = {{p}_{0}}\exp \left( { - \frac{z}{H}} \right) = {{\rho }_{0}}gH\exp \left( { - \frac{z}{H}} \right), \\ \bar {\rho }\left( z \right) = {{\rho }_{0}}\exp \left( { - \frac{z}{H}} \right). \\ \end{gathered} $

Здесь $\bar {p}(z)$ – фоновое давление газа, p₀ – давление газа у поверхности земли, ${\bar {\rho }}(z)$ – фоновая плотность газа, ρ₀ – плотность газа у поверхности земли, H – высота однородной атмосферы, z – текущее значение высоты.

Система уравнений термогидродинамики записывается в виде

$\frac{{\partial {\mathbf{V}}}}{{\partial t}} = - \frac{{\nabla p{\kern 1pt} '}}{{\bar {\rho }}} + {\mathbf{a}}\frac{{\rho {\kern 1pt} '}}{{\bar {\rho }}},$

$\frac{{\partial p{\kern 1pt} {\text{'}}}}{{\partial t}} = - {\mathbf{V}}\left( {\nabla {\text{\;}}\bar {p}} \right) - \gamma \bar {p}\left( {\nabla {\mathbf{V}}} \right),$

$\frac{{\partial \rho {\kern 1pt} {\text{'}}}}{{\partial t}} = - {\mathbf{V}}\left( {\nabla {\text{\;}}\bar {\rho }} \right) - \bar {\rho }\left( {\nabla {\mathbf{V}}} \right),$

где V – скорость потока газа, γ = C_p/C_v, a – вектор силового поля, компоненты которого в случае гравитационных сил есть a_x = 0, a_y = 0, a_z = g.

Далее удобно ввести новую переменную –

(1)

$\varphi {\kern 1pt} {\text{'}} = p{\kern 1pt} '\,\, - \gamma \frac{{\bar {p}}}{{\bar {\rho }}}\rho {\kern 1pt} {\text{',}}$

перейти к новым переменным –

(2)

$\begin{gathered} P = p{\kern 1pt} '\exp \left( {\frac{z}{{2H}}} \right),\,\,\,\,\Phi = \varphi {\kern 1pt} '\exp \left( {\frac{z}{{2H}}} \right), \\ {\mathbf{U}} = {\mathbf{V}}\exp \left( { - \frac{z}{{2H}}} \right), \\ \end{gathered} $

а также ограничиться рассмотрением одномерного случая. В итоге система имеет вид

(3)

$\frac{{\partial {{U}_{z}}}}{{\partial t}} = \frac{1}{{{{\rho }_{0}}}}\left( {\frac{{\gamma - 2}}{{2\gamma H}} - \frac{\partial }{{\partial z}}} \right)P + \frac{\Phi }{{\gamma H{{\rho }_{0}}}},$

(4)

$\frac{{\partial P}}{{\partial t}} = - \gamma gH{{\rho }_{0}}\frac{{\partial {{U}_{z}}}}{{\partial z}} - g{{\rho }_{0}}\frac{{\gamma - 2}}{2}{{U}_{z}},$

(5)

$\frac{{\partial \Phi }}{{\partial t}} = - \left( {\gamma - 1} \right)g{{\rho }_{0}}{{U}_{z}}{\text{\;}}.$

2.2. Постановка задачи распространения граничного режима

В качестве эволюционной переменной фигурирует вертикальная координата $z$. Перенесем в левую часть уравнений (3) и (4) производные по пространственной переменной. Заметим, что уравнение (5) не содержит таких производных, поэтому далее оно будет рассматриваться как уравнение связи. Используя (5), исключим из уравнений (3) и (4) U_z. В результате получим

(6)

$\frac{{\partial P}}{{\partial z}} = \frac{1}{{\left( {\gamma - 1} \right)g}}\frac{{{{\partial }^{2}}\Phi }}{{\partial {{t}^{2}}}} + \frac{{\gamma - 2}}{{2\gamma H}}P + \frac{\Phi }{{\gamma H}},$

(7)

$\frac{{{{\partial }^{2}}\Phi }}{{\partial z\partial t}} = \frac{{\gamma - 1}}{{\gamma H}}\frac{{\partial P}}{{\partial t}} - \frac{{\gamma - 2}}{{2\gamma H}}\frac{{\partial \Phi }}{{\partial t}},$

(8)

${{U}_{z}} = ~ - ~\frac{1}{{\left( {\gamma - 1} \right){{\rho }_{0}}g}}\frac{{\partial \Phi }}{{\partial t}}~.$

В задаче распространения акустического возмущения можно пренебречь энтропийной модой. Для того чтобы однозначно определить решение системы, необходимо и достаточно всего одного граничного условия. Исходя из физического смысла, граничный режим зададим для скорости: U_z(0, t) = F(t).

3. РЕШЕНИЕ ЗАДАЧИ

3.1. Общее решение задачи распространения граничного режима

Воспользуемся обратным преобразованием Фурье для основных величин системы уравнений

$P\left( {z,t} \right) = \frac{1}{{\sqrt {2\pi } }}\mathop \smallint \limits_{ - \infty }^\infty {{e}^{{i\omega t}}}p\left( {z,\omega } \right)d\omega ,~$

$\Phi \left( {z,t} \right) = \frac{1}{{\sqrt {2\pi } }}\mathop \smallint \limits_{ - \infty }^\infty {{e}^{{i\omega t}}}\phi \left( {z,\omega } \right)d\omega .$

Тогда система уравнений (6) и (7) примет вид

(9)

$\begin{gathered} \frac{{dp\left( {z,\omega } \right)}}{{dz}} = - \frac{{{{\omega }^{2}}}}{{\left( {\gamma - 1} \right)g}}\phi \left( {z,\omega } \right) + \\ + \,\,\frac{{\gamma - 2}}{{2\gamma H}}p\left( {z,\omega } \right) + \frac{{\phi \left( {z,\omega } \right)}}{{\gamma H}}, \\ \end{gathered} $

(10)

$\begin{gathered} \frac{{d\phi \left( {z,\omega } \right)}}{{dz}} = \frac{{\gamma - 1}}{{\gamma H}}p\left( {z,\omega } \right) - \frac{{\gamma - 2}}{{2\gamma H}}\phi \left( {z,\omega } \right), \\ {\text{if}}\,\,\omega \ne 0. \\ \end{gathered} $

Система уравнений (9), (10) – линейная однородная система обыкновенных дифференциальных уравнений с постоянными коэффициентами, зависящими от параметра ω. Общее решение такой системы существует в форме

$\phi \left( {z,\omega } \right) = {{C}_{1}}\left( \omega \right){{e}^{{ - k\left( \omega \right)z}}} + {{C}_{3}}\left( \omega \right){{e}^{{k\left( \omega \right)z}}},$

$p\left( {z,\omega } \right) = {{C}_{2}}\left( \omega \right){{e}^{{ - k\left( \omega \right)z}}} + {{C}_{4}}\left( \omega \right){{e}^{{k\left( \omega \right)z}}},$

где

$k\left( \omega \right) = {{\left( {\frac{1}{{4{{H}^{2}}}} - \frac{{{{\omega }^{2}}}}{{Hg\gamma }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}~.$

Однако мы будем считать, что от поверхности океана распространяется только волна вверх, поэтому решение будет иметь вид

(11)

$\phi \left( {z,\omega } \right) = D\left( \omega \right){{e}^{{ - k\left( \omega \right)z}}},$

(12)

$p\left( {z,\omega } \right) = B\left( \omega \right){{e}^{{ - k\left( \omega \right)z}}}.$

Рассмотрим решение при z = 0:

$\phi \left( {0,\omega } \right) = D\left( \omega \right) = \frac{1}{{\sqrt {2\pi } }}\mathop \smallint \limits_{ - \infty }^\infty {{e}^{{ - i\omega t}}}\Phi \left( {0,t} \right)dt,$

$p\left( {0,\omega } \right) = B\left( \omega \right) = \frac{1}{{\sqrt {2\pi } }}\mathop \smallint \limits_{ - \infty }^\infty {{e}^{{ - i\omega t}}}P\left( {0,t} \right)dt.$

Найдем уравнение (8) в ω-представлении:

(13)

${{u}_{z}}\left( {z,\omega } \right) = - \frac{{i\omega }}{{\left( {\gamma - 1} \right)g{{\rho }_{0}}}}\phi \left( {z,\omega } \right).$

Связь между p и ϕ установим с помощью операторов проектирования. Так как мы не рассматриваем волну, бегущую вниз, то, действуя оператором проектирования “вниз” на вектор состояния, мы должны получить

(14)

${{P}_{ \downarrow }}\Psi = 0$,

где

$\Psi = \left( {\begin{array}{*{20}{c}} {~p} \\ \phi \end{array}} \right).$

Решив (14), получим уравнение связи для p и ϕ:

(15)

$p\left( {z,\omega } \right) = - ~\frac{{2i{{\rho }_{0}}\left( {{{\omega }^{2}}\gamma H - g\gamma + g} \right)}}{{\omega \left[ {{{{\left( {{{\gamma }^{2}} - \frac{{4{{\omega }^{2}}\gamma H}}{g}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \gamma - 2} \right]}}\phi \left( {z,\omega } \right).$

3.2. Частное решение задачи распространения граничного режима

Пусть формула для граничного режима имеет вид

(16)

${{U}_{z}}\left( {0,t} \right) = A{{e}^{{ - \lambda t}}}$,

а фурье-образ граничного режима –

(17)

${{u}_{z}}\left( {0,\omega } \right) = \frac{1}{{\sqrt {2\pi } }}\mathop \smallint \limits_{ - \infty }^\infty {{e}^{{ - i\omega t}}}{{U}_{z}}\left( {0,t} \right)~dt = - \frac{1}{{\sqrt {2\pi } }}\frac{A}{{i\omega + \lambda }}.$

Используя (17), (15) и (13), найдем коэффициенты, входящие в уравнения (11) и (12):

$D\left( \omega \right) = \frac{A}{{\sqrt {2\pi } }}\frac{{\left( {\gamma - 1} \right)g{{\rho }_{0}}}}{{i\omega \left( {i\omega + \lambda } \right)}},$

$B\left( \omega \right) = - \frac{A}{{\sqrt {2\pi } }}\frac{{2i{{\rho }_{0}}\left( {{{\omega }^{2}}\gamma H - g\gamma + g} \right)}}{{\omega \left( {i\omega + \lambda } \right)\left[ {{{{\left( {{{\gamma }^{2}} - {{4{{\omega }^{2}}\gamma H} \mathord{\left/ {\vphantom {{4{{\omega }^{2}}\gamma H} g}} \right. \kern-0em} g}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \gamma - 2} \right]}}~.$

Наконец можно записать решение:

(18)

$\begin{gathered} \phi \left( {z,\omega } \right) = \frac{A}{{\sqrt {2\pi } }}\frac{{\left( {\gamma - 1} \right)g{{\rho }_{0}}}}{{i\omega \left( {i\omega + \lambda } \right)}} \times \\ \times \,\,\exp \left\{ { - z{{{\left( {\frac{1}{{4{{H}^{2}}}} - \frac{{{{\omega }^{2}}}}{{Hg\gamma }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right\}, \\ \end{gathered} $

(19)

$\begin{gathered} p\left( {z,\omega } \right) = \\ = \frac{{ - A}}{{\sqrt {2\pi } }}\frac{{2i{{\rho }_{0}}\left( {{{\omega }^{2}}\gamma H - g\gamma + g} \right)}}{{\omega \left( {i\omega + \lambda } \right)\left[ {{{{\left( {{{\gamma }^{2}} - {{4{{\omega }^{2}}\gamma H} \mathord{\left/ {\vphantom {{4{{\omega }^{2}}\gamma H} g}} \right. \kern-0em} g}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \gamma - 2} \right]}} \times \\ \times \,\,\exp \left\{ { - z{{{\left( {\frac{1}{{4{{H}^{2}}}} - \frac{{{{\omega }^{2}}}}{{Hg\gamma }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right\}. \\ \end{gathered} $

4. ПОСТРОЕНИЕ МНОГОСЛОЙНОЙ МОДЕЛИ

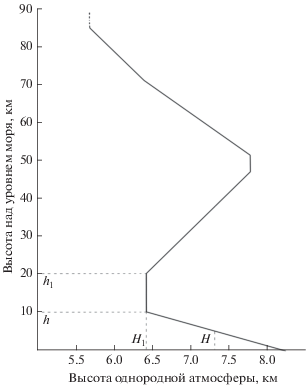
Модель многослойной атмосферы изображена на рис. 1. Выражение (18) является решением только в первом слое, т.е. при z $ \in $ [0, h]. На границе раздела первого и второго слоев, т.е. при z = h, оно имеет вид

(20)

$\phi \left( {h,\omega } \right) = D\left( \omega \right)\exp \left\{ { - h{{{\left( {\frac{1}{{4{{H}^{2}}}} - \frac{{{{\omega }^{2}}}}{{Hg\gamma }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right\}.$

Рис. 1.

Вертикальная структура распределения температуры и в приземном слое. Помечены модельные значения высот однородной атмосферы H, H₁, а также высот h, h₁ для первых двух слоев.

Во втором слое, т.е. при z $ \in $ [h, h₁],

(21)

${{\phi }_{1}}\left( {z,\omega } \right) = {{D}_{1}}\left( \omega \right)\exp \left\{ { - z{{{\left( {\frac{1}{{4{{H}_{1}}^{2}}} - \frac{{{{\omega }^{2}}}}{{{{H}_{1}}g\gamma }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right\},$

где ϕ₁(z, ω) – решение для второго слоя, H₁ – высота однородной атмосферы во втором слое.

Вернемся к физической величине из (1). Она такова, что

$\varphi {\kern 1pt} ' \in \left[ {0,h} \right],\,\,~\varphi _{1}^{'} \in \left[ {h,{{h}_{1}}} \right]\,\,{\text{и}}\,\,\varphi {\kern 1pt} '\left( h \right) = \varphi _{1}^{'}\left( h \right).$

Тогда из (2) следует соотношение

(22)

$\begin{gathered} \Phi \left( h \right)\exp \left( { - \frac{h}{{2H}}} \right) = {{\Phi }_{1}}\left( h \right)\exp \left( { - \frac{h}{{2{{H}_{1}}}}} \right)~, \\ {{\Phi }_{1}}\left( h \right) = \Phi \left( h \right)\exp \left( {\frac{h}{{2{{H}_{1}}}} - \frac{h}{{2H}}} \right)~. \\ \end{gathered} $

А в ω-представлении

${{\phi }_{1}}\left( {h,\omega } \right) = \phi \left( {h,\omega } \right)\exp \left( {\frac{h}{{2{{H}_{1}}}} - \frac{h}{{2H}}} \right)~.$

Сравнивая последний результат с формулой (21), получим

$\begin{gathered} {{D}_{1}}\left( \omega \right) = \phi \left( {h,\omega } \right)\exp \left( {\frac{h}{{2{{H}_{1}}}} - \frac{h}{{2H}}} \right) \times \\ \times \,\,\exp \left\{ {h{{{\left( {\frac{1}{{4{{H}_{1}}^{2}}} - \frac{{{{\omega }^{2}}}}{{{{H}_{1}}g\gamma }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right\}. \\ \end{gathered} $

Чтобы проиллюстрировать спектральную плотность скорости, найдем решение для этой величины в обоих слоях из уравнений (20) и (22):

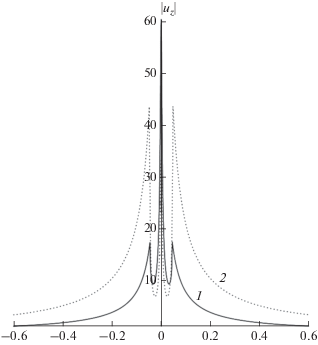
${{u}_{z}}\left( {z,\omega } \right) = - \frac{1}{{\sqrt {2\pi } }}\frac{A}{{\left( {i\omega + \lambda } \right)}}\exp \left\{ { - z{{{\left( {\frac{1}{{4{{H}^{2}}}} - \frac{{{{\omega }^{2}}}}{{Hg\gamma }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right\},$

$\begin{gathered} {{u}_{{z1}}}\left( {z,\omega } \right) = {{u}_{z}}\left( {z,\omega } \right)\exp \left( {\frac{h}{{2{{H}_{1}}}} - \frac{h}{{2H}}} \right) \times \\ \times \,\,\exp \left\{ {h{{{\left( {\frac{1}{{4{{H}_{1}}^{2}}} - \frac{{{{\omega }^{2}}}}{{{{H}_{1}}g\gamma }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right\} \times \\ \times \,\,\exp \left\{ { - z{{{\left( {\frac{1}{{4{{H}_{1}}^{2}}} - \frac{{{{\omega }^{2}}}}{{{{H}_{1}}g\gamma }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right\}. \\ \end{gathered} $

На рис. 2 графически представлена спектральная плотность скорости. Результаты могут быть использованы для моделирования вариаций химического и ионного составов атмосферного газа. Связи типа (14) могут быть также использованы и для решения диагностических задач по аналогии с работой [6].

Рис. 2.

Спектр возмущения на границах первых двух слоев при z = h = 10 000 м, z = h₁ = 20 000 м, H = 7300 м, H₁ = 6400 м, λ = 1/300, γ = 3/2, g = 9.8 м/с²: 1 – z = h, 2 – z = h₁.

5. ЗАКЛЮЧЕНИЕ

Важным шагом в сторону установления большей реалистичности предложенной модели было бы уточнение формулы для граничного режима, более соответствующего волне цунами. Так, в работе [7] предлагается функция (16), домноженная на тригонометрическую функцию. Такая модификация позволяет вычислить образ Фурье и скорректировать рабочую формулу (18). Мы не хотели загромождать изложение, увеличивая число слоев, а лишь хотели показать, как работает теория. В дальнейшем при вычислении ионосферного эффекта на высотах выше второго слоя, мы продолжим моделирование, тем более что формализм переносится на следующий слой почти автоматически. Для коррекции параметров модели могу быть использованы данные наблюдений в реальной атмосфере, как в работе [8]. Планируется также провести сравнение с результатами численного моделирования вертикального распространения акустических волн от наземных источников на основе данных, полученных в работе [9].

Работа выполнена при частичной поддержке Российским фондом фундаментальных исследований (проект № 18-05-00184).

Список литературы

Babich V.M. Buldyrev V.S., Kuester E.F. Short-wavelength Diffraction Theory: Asymptotic Methods. Berlin: Springer-Verlag, 1991.
Brekhovskikh L.M., Godin O.A. Acoustics of layered media. V. 1: Plane and quasi-plane waves. Heidelberg–Berlin: Springer-Vedag, 1991.
Hines C. O. // Nature. 1972. V. 239. P. 73.
Leble S., Perelomova A. // Appl. Mathemat. Modell. 2013. V. 37. № 3. P. 629; https://doi.org/10.1016/j.apm.2012.02.037
Zabotin N.A., Godin O.A., Bullett T.W. // J. Geophys. Res.: Space Physics, 2016. V. 121. P. 3452.
Лебле С.Б., Верещагин С.Д., Верещагина И.С. // Хим. физика. 2018. Т. 12. № 3. С. 554; https://doi.org/10.7868/S0207401X18050096
Dobrokhotov S., Minenkov D., Nazaikinskii V., Tirozzi B. // Operator Theory: Advances and Applications. 2013. V. 228. P. 95.
Бахметьева Н.В., Бубукина В.Н., Вяхирев В.Д. и др. // Хим. физика. 2017. Т. 36. № 12. С. 44; https://doi.org/10.7868/S0207401X17120056
Васильев П.А., Карпов И.В., Кшевецкий С.П. // Хим. физика. 2017. Т. 36. № 12. С. 56; https://doi.org/10.7868/S0207401X17120135

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Химическая физика

Архивы выпусков Информация о журнале Отправить рукопись в журнал