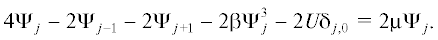Химическая физика, 2020, T. 39, № 6, стр. 3-6
Решение дискретного нелинейного уравнения Шредингера с ловушкой
В. Н. Лихачев 1, Г. А. Виноградов 1, *, Н. С. Эрихман 1
1 Институт биохимической физики им. Н.М. Эмануэля Российской академии наук
Москва, Россия
* E-mail: gvin@deom.chph.ras.ru
Поступила в редакцию 19.06.2019
После доработки 17.10.2019
Принята к публикации 21.10.2019
Аннотация
Волновую функцию и энергию основного состояния для дискретного нелинейного уравнения Шредингера с ловушкой можно найти численно с помощью итерационного процесса. Однако этот подход не всегда дает сходящийся результат. Предложен функционал, не являющийся функционалом энергии, минимум которого всегда дает основное состояние рассматриваемой системы.
ВВЕДЕНИЕ
Континуальное нелинейное уравнение Шредингера и его модификации имеют широкое применение для описания различных явлений: распространения света в нелинейных оптических срéдах и волноводах, давыдовских солитонов в биологических системах и некоторых других [1–4]. У этого уравнения есть его решеточный аналог – дискретное нелинейное уравнение Шредингера (ДНУШ). Это уравнение и его варианты также имеют обширные применения в решеточных моделях для анализа различных процессов; ДНУШ применимо в тех же областях, где и континуальное уравнение. Оно относительно легко решается численными методами, и вследствие этого имеются многочисленные примеры использования этого уравнения [5–12 ].
Дискретное нелинейное уравнение Шредингера является частным случаем более общего уравнения – дискретного уравнения с самозахватом [13]:
Некоторые практически интересные системы не являются однородными и могут содержать дефекты различной природы. В этих случаях для получения решения до сих пор применялись лишь численные методы. Однако, имея аналитические решения, полезно выяснить зависимость типа и характеристик последних от параметров задачи.
В настоящей работе решается задача о получении стационарного решения ДНУШ в решетке с единственным дефектом. Мы рассмотрели возможность получения основного состояния системы с помощью численных методов. Но оказалось, что диагонализация гамильтониана с последующей подстановкой промежуточного решения в гамильтониан не всегда является сходящимся итерационным процессом. Для линейных гамильтонианов минимум функционала $\left\langle {{\Psi }\left| H \right|{\Psi }} \right\rangle $ всегда совпадает с решением уравнения $H\left| {\Psi } \right\rangle = E\left| {\Psi } \right\rangle .$ Но для нелинейных гамильтонианов существование соответствующего функционала отнюдь не является очевидным. И в работе построен такой функционал, минимизация которого приводит к уравнению Шредингера.
РЕШЕНИЕ ДНУШ КАК ПОИСК МИНИМУМА ФУНКЦИОНАЛА
Находится основное состояние (энергия и волновая функция) заряда на бесконечной одномерной дискретной решетке, содержащей единственный примесный центр. Гамильтониан рассматриваемой системы в матричном представлении и в приближении сильной связи есть трехдиагональная матрица:
(1)
${{H}_{{j{\text{,}}j}}} = {\text{2}} - {\beta }{{\left| {{{{\Psi }}_{j}}} \right|}^{{\text{2}}}} - U{{{\delta }}_{{j{\text{,0}}}}},\,\,\,\,{{H}_{{j{\text{,}}j + {\text{1}}}}} = {{H}_{{j + {\text{1,}}j}}} = - {\text{1,}}$где Ψj – значение волновой функции на узле j. На главной диагонали находятся энергии взаимодействия с узлом, равные –β|Ψj|2. В случае β < 0 эта квадратичная нелинейность создает отталкивающий потенциал. Двойка в главной диагонали добавлена для того, чтобы дно зоны имело нулевую энергию. По сравнению со “стандартным” ДНУШ на узле j = 0 дополнительно находится ловушка глубиной U. На побочной диагонали интегралы перескока выбраны равными –1, что определяет масштаб энергии. Для стационарного ДНУШ волновые функции можно считать действительными. Тогда уравнение Шредингера имеет вид
(2)
${{\text{2}}{{{\Psi }}_{j}} - {{{\Psi }}_{{j - {\text{1}}}}} - {{{\Psi }}_{{j + {\text{1}}}}} - {\beta \Psi }_{j}^{{\text{3}}} - U{{{\delta }}_{{j{\text{,0}}}}}{{{\Psi }}_{j}} = E{{{\Psi }}_{j}}{\text{.}}}$Рассмотрим простой случай отсутствия нелинейности (β = 0). Электрон находится в локализованном состоянии на ловушке и волновая функция основного состояния экспоненциально убывает: Ψ(j) ~ q|j|. А именно, выражение для волновой функции имеет вид
(3)
$\begin{gathered} {\Psi (}j{\text{)}} = {{\left( {\frac{{{{U}^{{\text{2}}}}}}{{{\text{4}} + {{U}^{{\text{2}}}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}{{q}^{{|j|}}}{\text{,}}\,\,\,\,q \equiv {\text{0}}{\text{.5}}\left( {\sqrt {{\text{4}} + {{U}^{{\text{2}}}}} - U} \right), \\ E = {\text{2}} - \sqrt {{\text{4}} + {{U}^{{\text{2}}}}} . \\ \end{gathered} $Уравнение (2) решается методом итераций. Для этого начальную волновую функцию можно выбрать, например, в виде Ψj$\sim $ exp(–|j|). Затем необходимо нормировать это решение на 1 и подставить его в гамильтониан (1). После численной диагонализации получается новое значение волновой функции, которое вновь подставляется в гамильтониан, и т.д. В результате получается требуемое основное состояние нелинейной задачи – его энергия и волновая функция. Для достижения машинной точности ~10–15 обычно хватает 100 итераций. Заметим, что для нелинейных гамильтонианов сходимость итерационного процесса отнюдь не является очевидной. И, действительно, оказалось, что при некоторых значениях параметров итерационный процесс не сходится.
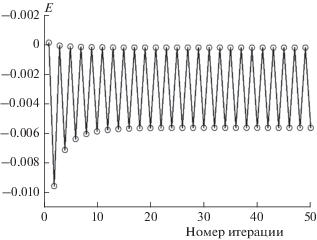
На рис. 1 показан пример отсутствия сходимости итерационного процесса для отрицательного значения параметра нелинейности β. Процесс осциллирует по энергии между двумя состояниями. Возможно, что несходимость связана с квазивырождением уровней энергии соответствующего гамильтониана; для малых значений N квазивырождение снимается и итерационный процесс сходится.
Рис. 1.
Зависимость энергии от номера итерации при U = 0.25, β = –0.25. Флуктуации энергии показаны только для 50 итераций, но они не исчезают и при дальнейших итерациях.
Однако существует другой способ численного нахождения энергии основного состояния. А именно, оказывается можно подобрать функционал, минимум которого для рассматриваемой задачи даст основное состояние. Этот функционал имеет следующий вид:
(4)
${{\Phi }\left\{ {\Psi } \right\} = {\text{2}}\sum\limits_i {{\Psi }_{j}^{{\text{2}}}} - {\text{2}}\sum\limits_i {{{{\Psi }}_{j}}{{{\Psi }}_{{j + {\text{1}}}}}} - \frac{{\beta }}{{\text{2}}}\sum\limits_i {{\Psi }_{j}^{{\text{4}}} - U{\Psi }_{{\text{0}}}^{{\text{2}}}} {\text{.}}}$Заметим, что первое слагаемое в (4) по условию нормировки равно двум. Оно оставлено в виде суммы для большей наглядности последующих соотношений. Заметим, что в обычном случае (в отсутствие нелинейности) минимум функционала $\left\langle {\Psi \left| H \right|\Psi } \right\rangle $ очевидным образом дает основное состояние. Однако предлагаемый функционал (3) отличается от $\left\langle {\Psi \left| H \right|\Psi } \right\rangle $ множителем (β/2 вместо β).
Для учета нормировки волновой функции добавим к функционалу (4) множитель Лагранжа μ и рассмотрим следующее выражение:
(5)
${\Omega }\left\{ {\Psi } \right\} \equiv {\Phi }\left\{ {\Psi } \right\} - {\mu }\left( {\sum\limits_i {{\Psi }_{j}^{{\text{2}}} - {\text{1}}} } \right).$Уравнения для минимума этого функционала (dΩ/dΨ = 0) имеют вид
Как видно, эти уравнения с точностью до множителя “2” совпадают с уравнением Шредингера (2). При этом множитель Лагранжа μ играет роль энергии. Отметим также, что минимизация функционала Φ{Ψ}, в отличие от метода итераций, всегда сходится к правильному результату.
Минимум функционала Φ{Ψ} можно искать методом градиентного спуска. Но при этом на каждом шаге будет необходимо восстанавливать нормировку волновой функции. Чтобы избежать этой трудности, удобнее использовать ту составляющую $\nabla \Phi ,$ которая перпендикулярна поверхности постоянной нормы. А именно, вместо градиента $\nabla \Phi $ для минимизации целесообразно использовать выражение $\nabla \Phi - {\Psi }\left( {{\Psi }\nabla {\Psi }} \right).$ Найденная волновая функция подставляется в выражение для энергии $\left\langle {\Psi \left| H \right|\Psi } \right\rangle {\text{:}}$
(7)
${E\left\{ {\Psi } \right\} = {\text{2}}\sum\limits_j {{\Psi }_{j}^{{\text{2}}}} - {\text{2}}\sum\limits_j {{{{\Psi }}_{j}}{{{\Psi }}_{{j + {\text{1}}}}}} - {\beta }\sum\limits_j {{\Psi }_{j}^{{\text{4}}} - U{\Psi }_{{\text{0}}}^{{\text{2}}}} {\text{.}}}$Отметим также, что возможность построения функционала, минимум которого дает основное состояние, носит более общий характер, чем изучаемый конкретный случай. Действительно, рассмотрим гамильтониан с произвольной диагональной нелинейностью F(Ψi):
Тогда соответствующий функционал будет иметь следующий вид:
где функция f(x) связана с функцией F(x) соотношением df/dx = 2xF(x). Можно также рассмотреть случай недиагональной нелинейности, например хорошо известный случай приближения сильной связи ~ΨjΨj+ 1. Оказалось, что и тогда для гамильтониана можно подобрать соответствующий функционал.
Так как волновая функция основного состояния симметрична относительно узла j = 0, то при поиске минимума функционала Φ{Ψ} можно вдвое уменьшить число переменных, и тогда $j \in {\text{[0,}}N{\text{]}}{\text{.}}$ В этом случае минимизируемый функционал (4) и условие нормировки приобретают следующий вид:
(8)
$\begin{gathered} \Phi \left\{ \Psi \right\} = - {\text{4}}\sum\limits_{j = {\text{0}}}^N {{{{\Psi }}_{j}}{{{\Psi }}_{{j + {\text{1}}}}}} - {\beta }\sum\limits_{j = {\text{1}}}^N {{\Psi }_{j}^{{\text{4}}}} - \frac{{\beta }}{{\text{2}}}{\Psi }_{{\text{0}}}^{{\text{4}}} - U{\Psi }_{{\text{0}}}^{{\text{2}}}, \\ {\Psi }_{{\text{0}}}^{{\text{2}}} + {\text{2}}\sum\limits_{j = {\text{1}}}^N {{\Psi }_{j}^{{\text{2}}}} = {\text{1}}{\text{.}} \\ \end{gathered} $Слагаемое ${\text{2}}\sum {{\Psi }_{j}^{{\text{2}}}} $ в первой строке (8) опущено, так как по условию нормировки оно равно двум.
Чтобы убедиться в достаточной длине N изучаемых решеток, рассмотрен случай и циклических граничных условий. При этом к
гамильтониану (1) необходимо добавить матричные элементы HN,–N = H–N,N = –1, а к функционалу Φ{Ψ} для соблюдения нормировки нужно добавить член 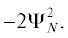
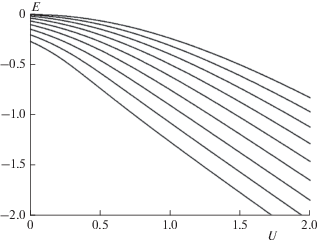
На рис. 2 показана зависимость энергии основного состояния от значений параметров β и U. Вычисления проводились как методом итераций (когда этот метод сходится), так и минимизацией функционала Φ{Ψ}. Совпадение результатов обоих методов составило ~10–15.
Рис. 2.
Энергия основного состояния как функция глубины ловушки U при разных значениях параметра β. Кривые сверху вниз: β = 0, 0.25, 0.5, …, 2.0. Кривая для случая β = 0 построена по формулам (3).
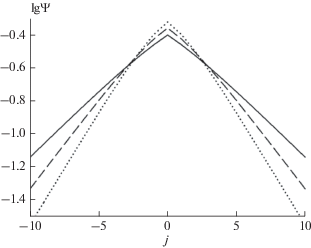
Волновые функции уже на небольшом удалении (|j| ≥ 5) от примесного узла спадают экспоненциально, но на узле j = 0 производные претерпевают излом. На рис. 3 в качестве примера показаны волновые функции для разных значений параметра β при глубине ловушки U = 0.25.
ЗАКЛЮЧЕНИЕ
Задачу решения ДНУШ с ловушкой можно решать численно для уравнения Шредингера, однако итерационный процесс, необходимый для получения решения, сходится не всегда. Предложен оригинальный способ, позволяющий обойти эту проблему. Подход заключается в построении функционала Ω{Ψ}, который в общем случае не является функционалом $\left\langle {\Psi \left| H \right|\Psi } \right\rangle $ исходного гамильтониана. Требование к этому функционалу состоит в том, чтобы производная dΩ/dΨ приводила (с точностью до известных коэффициентов) к правильному уравнению Шредингера. Минимизация полученного функционала, например модифицированным методом наискорейшего спуска, всегда приводит к получению энергии основного состояния и волновой функции. В тех случаях, когда итерационный процесс сходится, достигается совпадение метода итераций и минимизации функционала ~10–15.
Список литературы
Kevrekidis P.G., Rasmussen K.Ø., Bishop A.R. // Intern. J. Mod. Phys. B. 2001. V. 15. P. 2833.
Eisenberg H.S., Silberberg Y., Morandotti R., Boyd A.R., Aitchison J.S. // Phys. Rev. Lett. 1998. V. 81. P. 3383.
Trombettoni A., Smerzi A. // Ibid. 2001. V. 86. P. 2353.
Abdullaev F.Kh., Baizakov B.B., Darmanyan S.A., Konotop V.V., Salerno M. // Phys. Rev. A. 2001. V. 64. P. 043606.
Springer Tracts in Modern Physics / Eds. Fujimori A., Kühn J., Müller Th., Steiner F., Trümper, Wölfle P. V. 232. Berlin-Heidelberg: Springer-Verlag. 2009.
Eilbeck J.C., Johanson M. // Localization and energy transfer in nonlinear systems / Eds. Vázquez L., MacKay R.S., Paz Zorzano M., New Jersey, London, Singapore, Hong Kong: World Scientific, 2003. P. 44.
Ablowitz M.J., Prinari B., Trubatch A.D. Discrete and continuous nonlinear Schrödinger systems. Cambridge University Press. 2004. P. 46.
Scharf R., Bishop A.R. // Phys. Rev. A. 1991. V. 43. P. 6535.
Molkenthin N., Hu S., Niemi A.J. // Phys. Rev. Lett. 2011. V. 106. P. 078102.10.
Астахова Т.Ю., Кашин В.А., Лихачев В.Н., Виноградов Г.А. // Хим. физика. 2016. Т. 35. № 12. С. 1.
Лихачев В.Н., Виноградов Г.А. // Хим. физика. 2018. Т. 37. № 6. С. 63.
Лихачев В.Н., Виноградов Г.А. // Хим. физика. 2018. Т. 37. № 12. С. 42.
Eilbeck J.C., Lomdahl P.S., Scott A.C. // Physica D. 1985. V. 16. P. 318.
Hasegawa A. Optical Solitons in Fibers. Berlin: Springer-Verlag, 1989.
Dmitriev S.V., Kevrekidis P.G., Yoshikawa N., Frantzeskakis D.J. // J. Phys. A: Math. Theor. 2007. V. 40. P. 1727.
Dmitriev S.V., Kevrekidis P.G., Sukhorukov A.A., Yoshikawa N., Takeno S. // Phys. Lett. A 2006. V. 356. P. 324.
Pelinovsky D.E. // Nonlinearity. 2006. V. 19. P. 2695.
Pelinovsky D.E., Melvin T.R.O., Champneys A.R. // Physica D. 2007. V. 236. P. 22.
Pelinovsky D.E., Rothos V.M. // Ibid. 2005. V. 202. P. 16.
Qin W.-X., Xiao X. // Nonlinearity. 2007. V. 20. P. 2305.
Jenkinson M., Weinstein M.I. // Ibid. 2016. V. 29. P. 27.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика