Химическая физика, 2020, T. 39, № 7, стр. 72-81
Поведение атомов лития в плоской силиценовой поре, находящейся на медной подложке. Компьютерный эксперимент
А. Е. Галашев 1, 2, *, О. Р. Рахманова 1, 2, А. В. Исаков 1
1 Институт высокотемпературной электрохимии Уральского отделения
Российской академии наук
Екатеринбург, Россия
2 Уральский федеральный университет имени первого Президента России Б.Н. Ельцина
Екатеринбург, Россия
* E-mail: alexander-galashev@yandex.ru
Поступила в редакцию 13.05.2019
После доработки 11.07.2019
Принята к публикации 22.07.2019
Аннотация
В молекулярно-динамическом эксперименте рассмотрены процессы литизации/делитизации в плоской щелевидной поре, образованной из дефектных листов силицена и находящейся на медной подложке. В зависимости от типа дефектов (моно-, би-, три-, гексавакансии) такая пора, не разрушаясь, может удерживать 67, 86, 60, 23 атома лития на протяжении всего молекулярно-динамического расчета продолжительностью до 1 нс. В результате прохождения цикла интеркаляции/деинтеркаляции структура дефектного силицена изменилась, особенно сильно в присутствии три- и гексавакансий. С ростом размера дефектов усиливается также подвижность атомов лития в силиценовой поре. После делитизации форма листов силицена не восстанавливается, а объем заключенного между ними пространства изменяется незначительно. Результативное применение силицена в литий-ионных батареях предполагает наличие в его листах только моно- и бивакансий.
ВВЕДЕНИЕ
Использование батарей с высокой плотностью энергии, длительным сроком службы и низкой стоимостью является ключевым фактором для бытовой электроники, электромобилей и хранения энергии в сетях [1–3]. Работа литий-ионных батарей основана на явлении интеркаляции лития в материал электрода. При зарядке батареи происходят экстракция лития из материала положительного электрода и его внедрение в материал отрицательного электрода, чаще всего изготавливаемого из графита. При разрядке эти процессы меняются на обратные. Одна из основных характеристик электрода – его интеркаляционная емкость, определяемая как количество электричества, сообщаемое электроду при полной зарядке, в расчете на единицу массы или объема. В частности, при полной зарядке углеродного электрода интеркаляционная емкость составляет 372 мА · ч/г. Эта характеристика для кремниевого электрода имеет значение 4200 мА · ч/г [4]. Скорость реакции интеркаляции/деинтеркаляции определяется скоростью диффузии лития в твердой фазе. Коэффициент диффузии лития в процессе литизации/делитизации, например, в двухслойном графене при комнатной температуре составляет 7 · 10–5 см2/с [5]. Чтобы избежать значительного изменения объема (почти четырехкратного в случае применения кристаллического кремния) при интеркаляции лития, предлагается использовать отрицательные электроды из тонкопленочных материалов [6–10]. Автономный двухслойный силицен не испытывает значительных структурных изменений во время циклов литизации/делитизации, а изменение объема составляет не более 25%, причем энергетический барьер для диффузии лития довольно низкий (<0.6 эВ) [11]. Силицен, находящийся на медной подложке, является полупроводником n-типа. В этом случае гибридизация между двумерной структурой и подложкой настолько сильная, что конус Дирака в зонной структуре силицена пропадает [12]. Однако при интеркаляции в систему атомов щелочного металла дираковские фермионы могут быть восстановлены. Существует достаточно много данных о свойствах силицена, находящегося на серебряной подложке [7, 13, 14], однако другие материалы подложек все еще остаются неосвоенными. Медь является наиболее широко используемым металлом в электрохимических приборах. Она имеет относительно невысокую стоимость и большую распространенность в земной коре (по сравнению с серебром). Эксперимент [15] и молекулярно-динамические (МД) исследования [16] говорят о формировании аморфной структуры на границе Cu/Si(001) двух объемных фаз, причем в зависимости от температуры подложки взаимная диффузия может достигнуть глубины до 10 нм [17]. Свойства силицена, расположенного на Cu-подложке, пока еще малоизучены.
Цели данной работы – молекулярно-динамическое исследование поведения функционализированного двухслойного силицена, находящегося на медной подложке, в ходе процессов литизации/делитизации, определение кинетических и динамических свойств системы и оценка возможности его применения в качестве анода литий-ионной батареи.
МОЛЕКУЛЯРНО-ДИНАМИЧЕСКАЯ МОДЕЛЬ
В качестве многочастичного потенциала взаимодействия атомов кремния в силицине мы выбрали модельный потенциал Терсоффа [18] с параметрами из работы [19]. Для описания межатомных взаимодействий в медной подложке использован потенциал погруженного атома EAM [20]. Между парами Cu–Si, Si–Si (принадлежащими разным листам), Cu–Li, Si–Li, Li–Li действовал потенциал Морзе с параметрами из работ [21–23], а также параметрами, рассчитанными через интерполяционные соотношения [4].
Рассматриваемая модель силицена представляет собой реконструкцию поверхности 4 × 4. Единичная ячейка содержит 18 атомов Si, расположенных в форме ромба. Шесть из них смещены на расстояние 0.074 нм перпендикулярно поверхности вверх для верхнего силиценового листа и вниз – для нижнего. Моделировалась плоская щелевидная пора (ЩП), сформированная двумя листами силицена, находящимися на подложке Cu(111). Величина зазора поры ${{h}_{g}}$ (расстояние между листами) составляла 0.75 нм. Проведенные ранее расчеты по изучению поведения иона лития в силиценовой поре [6] показали, что именно при таком зазоре входящий в пору Li+ может находиться в ней не менее 100 пс, взаимодействуя со стенками поры.
Листы силицена имели прямоугольную форму размером 4.7 × 4.0 нм. При наличии совершенной структуры они содержали по 300 атомов Si. В силицене создавались дефекты различного размера: в девяти местах, приблизительно равномерно размещенных по площади листов, удалялось по 1, 2, 3 и 6 атомов кремния, и таким образом формировались моно-, би-, три- и гексавакансии. Экспериментальные данные свидетельствуют о наличии дефектов в силицене вне зависимости от используемой для его получения подложки [24].
Двухслойный силицен располагался в соответствии с укладкой Бернала (ABAB…) на неподвижной, но взаимодействующей с силиценом подложке Cu(111). Закрепление краев силиценовых листов позволяет избежать их нефизичных поворотов, связанных с присутствием нескомпенсированных локальных вращательных моментов [1, 2]. Рассчитанное согласно теории функционала плотности расстояние ${{r}_{{{\text{Cu}} - {\text{Si}}}}}$ между нижним листом силицена и металлической подложкой составляет 0.2481 нм [25]. Однако предварительные расчеты с использованием такого значения зазора между подложкой и силиценовыми листами показали непрерывное отдаление последних от медной подложки при интеркаляции лития. Поэтому значение ${{r}_{{{\text{Cu}} - {\text{Si}}}}}$ было увеличено до 0.27 нм, что соответствует данным работы [26]. Молекулярно-динамические расчеты всех систем проводились в NVT-ансамбле при температуре 300 K.
Для предотвращения сильного выгибания листов силицена в центре ЩП между ними на равном расстоянии вертикально были размещены два шестизвенных циклических образования (в виде “колонны”), в узлах которых находились атомы Si. Эта стабилизирующая структура была неподвижна, однако взаимодействовала с атомами Li и Si посредством потенциала Морзе [22, 23]. Моделирование заполнения изначально пустотелой силиценовой ЩП, находящейся на медной подложке, показало появление значительного прогиба листов силицена [7]. Введение вертикальной стабилизирующей поддержки между листами силицена позволяет этого избежать [27]. Введение “колонны” в ЩП выразилось в уменьшении деформации листов силицена, особенно содержащих крупные дефекты вакансионного типа. Это позволило сделать наполнение ЩП литием более значительным. В отсутствие “колонны” наполняемость поры снижалась на 20–30%.
Процесс литизации двухслойного силицена на подложке осуществлялся посредством периодического (через каждые 10 пс) попарного добавления в систему ионов лития. Первоначальное положение пары ионов Li+ выбиралось случайным образом на линии, параллельной оси y и находящейся вблизи входа в пору на уровне ${{{{h}_{g}}} \mathord{\left/ {\vphantom {{{{h}_{g}}} 2}} \right. \kern-0em} 2}.$ Предварительно, до реализации процесса интеркаляции, была проведена процедура релаксации системы в течение 200 пс. Затем ионы лития запускались в ЩП через промежутки времени 10 пс, или 105$\Delta t,$ где $\Delta t$ = = 1 ⋅ 10–16 с – величина временнóго шага. Экспериментально установлено, что при интеркаляции ион Li+, проникая в анод, быстро приобретает электрон и становится нейтральным атомом [28]. В ходе обратного процесса (деинтеркаляции) атомы Li захватывают электроны и в виде ионов устремляются к катоду. Такая перезарядка всегда происходит в кремнии, но не происходит в углеродных материалах (например, графите). Продолжительность расчета в 10 пс достаточна для вычисления равновесных свойств системы (полной энергии и тензора напряжений) и коэффициентов подвижности атомов. Кроме того, на таком интервале ионы могут с большой вероятностью найти энергетически выгодные места в ЩП и оставаться в них.
Электрическое поле величиной 103 В/м имело вектор напряженности, направленный вдоль оси x. Заряды (ионы) двигались по поре под действием этого электрического поля, испытывая кулоновское отталкивание по отношению друг к другу. По прошествии 10 пс эти пополнившие ЩП ионы становились атомами и в дальнейшем в ходе интеркаляции оставались электрически нейтральными. Такой временнóй интервал был достаточен для расчета тензора напряжений силицена и коэффициента подвижности атомов Li. Процесс интеркаляции прекращался, когда система начинала разрушаться (при наличии гексавакансий) или ионы и атомы лития начинали активно покидать ЩП. Например, процесс заполнения литием силиценовой поры, сконструированной из листов с моновакансиями, длился 0.75 нс. Кроме визуального наблюдения за системой, индикатором заполнения ЩП служил скачок полной энергии системы.
Процесс делитизации в обратном направлении происходил путем попарного выведения ионов лития из поры. После удаления из рассмотрения ионов Li+, уже покинувших пору на предыдущем этапе, новая пара ионов начинала двигаться под действием электрического поля величиной 105 В/м, направленного в обратном направлении вдоль оси x. Напряженность электрического поля, поддерживающего процесс деинтеркаляции, была увеличена для преодоления ионами энергетического барьера, связанного с их выходом из ЩП. Время наблюдения за выходом пары ионов из ЩП в этом случае было увеличено до 200 000 временны́х шагов (20 пс). В расчетах использовались модифицированные нами коды программного комплекса LAMMPS [29], который запускался на гибридном вычислителе кластерного типа “УРАН” при ИММ УрО РАН.
Коэффициент подвижности (D) атомов лития в ЩП рассчитывался через средний квадрат смещения атомов – $\left\langle {{{{\left[ {\Delta {\mathbf{r}}(t)} \right]}}^{2}}} \right\rangle {\text{:}}$
(1)
$D = \mathop {\lim }\limits_{t \to \infty } \frac{1}{{2\Gamma t}}{{\left\langle {{{{\left[ {\Delta {\mathbf{r}}(t)} \right]}}^{2}}} \right\rangle }_{{{{t}_{0}}}}}.$Для расчета напряжений, возникающих в силицене, листы разбивались на элементарные площадки. Напряжения ${{\sigma }_{{u{\alpha }}}}(l),$ возникающие в направлении действия сил $\alpha $ = x, y, z, вычисляются на каждой площадке с номером l, имеющей ориентацию, определяемую направлением u = x, y, x. В этих расчетах используются произведения проекций скоростей атомов и значения проекции сил $f_{{ij}}^{{\alpha }},$ действующих на l-площадку со стороны других атомов при соблюдении соответствующих условий [30]:
(2)
${{\sigma }_{{u{\alpha }}}}(l) = \left\langle {\sum\limits_i^k {\frac{1}{\Omega }\left( {m{v}_{u}^{i}{v}_{{\alpha }}^{i}} \right)} } \right\rangle + \frac{1}{{{{S}_{l}}}}\left\langle {\sum\limits_i^k {\sum\limits_{j \ne i}^{({{u}_{i}} \leqslant u,\,{{u}_{j}} \geqslant u)} {\left( {f_{{ij}}^{{\alpha }}} \right)} } } \right\rangle .$РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
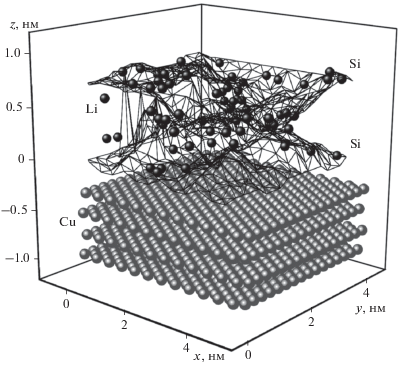
Силиценовая ЩП, находящаяся на подложке Cu(111), после полной интеркаляции литием изображена на рис. 1 в виде тонкой паутины, чтобы показать все осажденные на стенки поры атомы Li. Видно, что размещение атомов Li в поре неравномерное. Первая половина поры по направлению оси x заполнена атомами Li значительно плотнее, чем вторая половина: 33 атома Li имеют координату x ≤ 2.6 нм и только 15 атомов Li размещаются в пространстве с координатой x > 2.6 нм. В средней части нижнего листа силицена наблюдается выпуклость по отношению к подложке, а в той же части верхнего листа – вогнутость. Значительное сужение поры в средней части затрудняет ее прохождение ионами Li+ и ограничивает заполняемость поры литием.
Рис. 1.
Щелевидная пора, образованная силиценовыми листами с моновакансиями и находящаяся на подложке Cu(111), после интеркаляции лития.
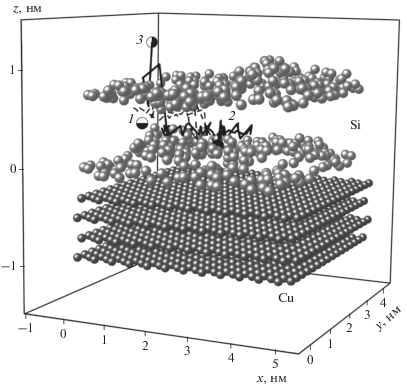
Траектория движения иона лития в щелевидной поре (листы которой заполнены тривакансиями) в процессе литизации (штриховая линия) и делитизации (сплошная линия) показана на рис. 2. Цифрами 1, 2 и 3 обозначены следующие точки: входа иона в пору, закрепления иона в ЩП после литизации и выхода иона из поры после делитизации соответственно. За время литизации (10 пс) ион успевает преодолеть барьер на вход в ЩП [6], продвинуться внутрь поры на расстояние, примерно равное половине длины ЩП (~2.5 нм), и закрепиться в “седловой” точке, чаще всего над центром шестизвенного Si-кольца. При дальнейшей литизации теперь уже атом Li может совершать небольшие колебательные движения в окрестности точки закрепления в поре. Во время делитизации, вновь приобретая заряд, ион лития начинает двигаться по направлению поля к выходу из поры и успевает покинуть ЩП за 20 пс. Следует отметить, что наблюдается корреляция между размером вакансионных дефектов в листах силицена и скоростью делитизации ЩП: чем больше вакансия, тем быстрее ион лития покидает щелевидную пору.
Рис. 2.
Траектория движения иона лития в процессе литизации (штриховая линия) и делитизации (сплошная линия) в силиценовой щелевидной поре, содержащей тривакансии, на подложке Cu(111): 1 – точка начала траектории иона (перед входом в канал) в момент времени t = 0 пс, 2 – конечная точка траектории иона после литизации, 3 – конечная точка траектории иона после делитизации.
Максимальное количество атомов Li, внедренных в силиценовые ЩП с разным типом вакансионных дефектов, приведено в табл. 1. Для сравнения здесь приводятся результаты внедрения лития при нахождении ЩП на подложке Ag(111) в отсутствие “колонны” между листами силицена. Видно, что в пригодных для реального использования случаях, т.е. для совершенного силицена и силицена с моно- и бивакансиями, число внедренных в пору атомов Li заметно больше, когда листы силицена лежат на медной подложке. Расчеты для пор с три- и гексавакансиями показали нежизнеспособность этих конструкций из-за значительных структурных перестроек в силицене и начавшегося разрушения его листов.
Таблица 1.
Максимальное количество атомов лития, вмещаемых в силиценовый канал, содержащий различные типы вакансий и находящийся на серебряной и медной подложках
| Тип вакансии в листах силицена | Тип подложки | |
|---|---|---|
| серебро | медь | |
| Совершенный | 39 | 48 |
| Моновакансии | 51 | 67 |
| Бивакансии | 71 | 86 |
| Тривакансии | 79 | 60 |
| Гексавакансии | 42 | 23 |
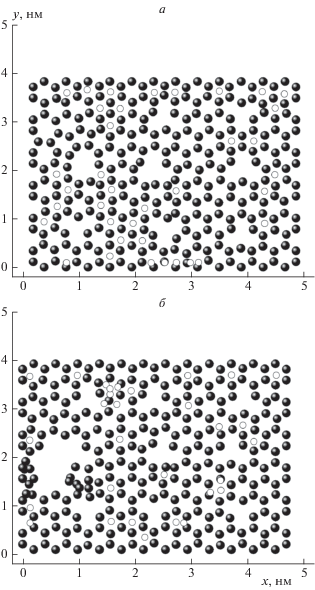
Рассмотрим более подробно поведение дефектов и принадлежность атомов Li к листам силицена на примере полностью заполненной литием силиценовой поры с моновакансиями. Исследуемые конфигурации относятся к моменту времени 0.75 нс (или 7.5 · 106Δt). Xy-проекции верхнего (а) и нижнего (б) слоев разрезанной средней плоскостью (z = ${{{{h}_{g}}} \mathord{\left/ {\vphantom {{{{h}_{g}}} 2}} \right. \kern-0em} 2}$) поры показаны на рис. 3 (вид со стороны плоскости z = ${{{{h}_{g}}} \mathord{\left/ {\vphantom {{{{h}_{g}}} 2}} \right. \kern-0em} 2}$). Одна из моновакансий нижнего листа трансформировалась в большое полое образование, что, по-видимому, есть проявление разрушительного воздействия медной подложки на силицен. В верхнем листе наблюдается трансформация некоторых моновакансий в циклические образования овальной формы, содержащие от 7 до 9 атомов Si. Восемь моновакансий нижнего листа и семь моновакансий верхнего листа деформировались, но сохранили свою первоначальную форму. Верхняя и нижняя части поры имеют равновеликие объемы, однако число атомов Li в них различно: 37 атомов находятся в верхней части и 30 атомов присутствуют в нижней части. Находящиеся в ЩП атомы лития располагаются преимущественно над центрами шестизвенных кремниевых колец.
Рис. 3.
Xy-проекции верхнего (а) и нижнего (б) листов силицена с моновакансиями на подложке Cu(111) в момент полного литиирования (67 атомов лития находятся в поре): ⚫ – атомы Si, ⚪ – атомы Li.
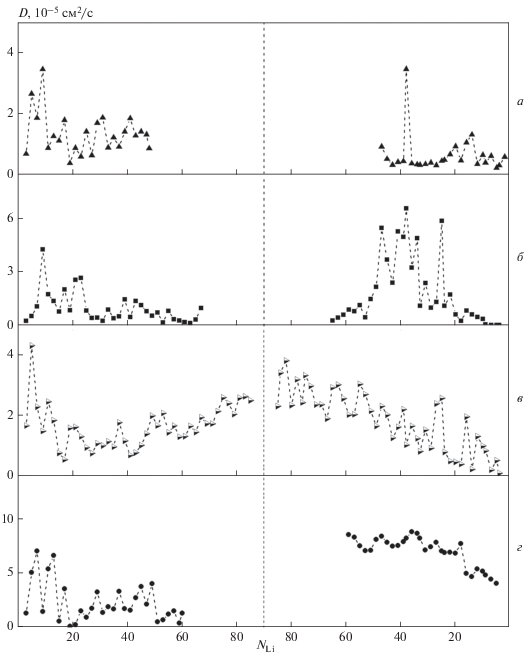
Поведение коэффициента подвижности D атомов Li в ЩП в процессах интеркаляции и деинтеркаляции непредсказуемо (рис. 4). Общей чертой поведения D во всех рассмотренных случаях является его высокие значения на начальном участке интеркаляции. Это естественно, так как при небольшом числе атомов Li в поре им передается от ионов Li+ большее удельное значение импульса, которое и приводит к увеличению значения коэффициента D. Однако, когда число атомов Li в ЩП становится больше 20, рельеф стенок поры начинает оказывать сильное влияние на подвижность атомов Li. В связи с этим величина D может как уменьшаться при наличии моновакансий (рис. 4б), так и увеличиваться в случае бивакансий (рис. 4в). Также коэффициент D достаточно непредсказуемо ведет себя при деинтеркаляции. Эта величина подвержена резким (для совершенного силицена (рис. 4а)) и продолжительным (для силицена с моновакансиями) изменениям в ходе делитизации. Значения D также могут снижаться при деинтеркаляции посредством флуктуаций, как это имеет место в присутствии в силицене бивакансий, или почти непрерывно, когда в силицене присутствуют тривакансии (рис. 4г). В случае силицена с тривакансиями наблюдается достаточно сильная перестройка структуры в обоих листах силицена. Однако в верхнем листе часть дефектов сохраняет свой вид. Вертикальное искажение листов после процесса литизации/делитизации не столь значительное.
Рис. 4.
Зависимость коэффициента подвижности атомов лития (D) в процессе интеркаляции (слева) и деинтеркалирования (справа) в силиценовых щелевидных порах с совершенным силиценом (а) и силиценом, имеющим моно- (б), би- (в) и тривакансии (г), от числа атомов лития (NLi).
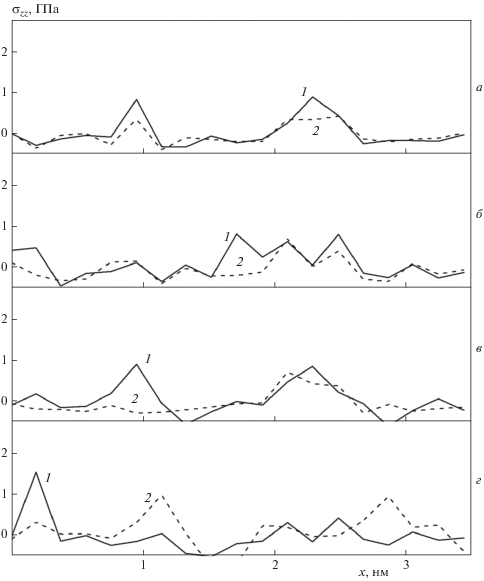
Как для совершенного, так и дефектного силицена напряжения σzx и σzy, связанные с введением в ЩП ионов (атомов) лития, заметно уступают напряжениям σzz, появляющимся в стенках поры. На рис. 5 показаны средние для верхнего (1) и нижнего (2) листов силицена распределения напряжений σzx и σzz, полученные при полном заполнении ЩП литием. Эти распределения относятся к случаю, когда разбивка листов на элементарные площадки продвигалась вдоль направления x (“зиг-заг”), а сами элементарные площадки вытянуты вдоль направления y (“кресло”). При такой разбивке получены наиболее сильные напряжения σzz, обусловленные внедрением лития в ЩП. Эти напряжения вызваны силами вертикального направления. Как видно из рис. 5, при интеркаляции лития сильные локальные напряжения σzz появляются в листах совершенного силицена (а), а также силицена, имеющего бивакансии (в) и тривакансии (г). Распределения напряжений в листах силицена с гексавакансиями (д) в целом похожи на соответствующие распределения в листах с тривакансиями (на рис. 5 не показаны). При деинтеркаляции напряжения σzz остаются более значительными в листах силицена с бивакансиями. Достигнутые максимальные значение σzz при интеркаляции составляют приблизительно 17–19% от предельного напряжения силицена при растяжении (20.45 ГПа) [31] и не являются критичными.
Рис. 5.
Распределение σzz-напряжений в силиценовых листах, образующих плоскую щелевидную пору, находящуюся на подложке Cu(111), когда пора заполняется литием до предела, в зависимости от типа дефектов: а – совершенный силицен, б – моно-, в – би-, г – тривакансии; 1 – верхний и 2 – нижний листы силиценовой ЩП; NLi = 48, 67, 86, 60 (сверху вниз).
ЗАКЛЮЧЕНИЕ
Согласно проведенным расчетам, используемый в литий-ионных батареях силицен должен иметь дефекты только в виде моно- и бивакансий. Применение совершенного силицена и силиценовой структуры с такими дефектами в среднем на 20% увеличивает число адсорбированных атомов Li по сравнению со случаем использования для поддержки силицена серебряной подложки. Применение силицена с дефектами в виде три- и гексавакансий, расположенного на медной подложке, в качестве анодного материала приводит не только к сокращению (по отношению к малоразмерным вакансионным дефектам) числа адсорбированных атомов Li, но также к разрушению материала анода.
В ходе реального физического эксперимента получить дефектную двумерную структуру гораздо проще, чем совершенную. Неконтролируемые дефекты могут образовываться самопроизвольно. Контроль за формированием вакансий определенного размера можно осуществлять с помощью сканирующей зондовой литографии [32] или ионной бомбардировки [33, 34]. В первом случае двумерную структуру можно модифицировать с довольно высокой точностью. А во втором – диаметр сканирующей области, как правило, составляет всего несколько нанометров, что позволяет выполнить быстрое сканирование поверхности и корректировку размера вакансий. Моно- и бивакансии являются энергетически выгодными дефектами и могут быть устойчивыми при достаточно высоких температурах [35].
Ионы и атомы лития, интеркалированные в совершенную силиценовую ЩП и пору с моно- или бивакансиями, расположенную на медной подложке, имеют приблизительно одинаковую скорость диффузии. Скорость диффузии увеличивается более чем на порядок при использовании силицена с три- и гексавакансиями. Однако неустойчивость такой силиценовой структуры не позволяет воспользоваться этим преимуществом. Предпочтительным размещением атома Li в силиценовой поре является местоположение, находящееся над центром гексагонального Si-кольца. На краях силиценовых листов атомы Li расположены преимущественно над (или под) атомами Si. Напряжения σzz, действующие в плоскости листов силицена и вызванные силами межатомного взаимодействия, направленными перпендикулярно этим плоскостям, являются доминирующими при интеркаляции лития в пору. Напряженное состояние стенок силиценовой ЩП не является однородным, но в результате движения атомов и ионов лития в поре появляются всплески напряжений, величина которых не превосходит 19% от предельного растягивающего напряжения силицена.
Исследование проведено в рамках бюджетной тематики Института высокотемпературной электрохимии УрО РАН, номер государственной регистрации темы АААА-А19-119020190046-5.
Список литературы
Галашев А.Е., Зайков Ю.П. // ЖФХ. 2015. Т. 89. № 12. С. 1899; https://doi.org/10.7868/S0044453715120122
Галашев А.Е., Зайков Ю.П. // Электрохимия. 2015. Т. 51. № 9. С. 983; https://doi.org/10.7868/S0424857015090054
Галашев А.Е., Рахманова О.Р. // Теплофизика высоких температур. 2016. Т. 54. № 1. С. 13; https://doi.org/10.7868/S0040364415050129
Галашев А.Е., Зайков Ю.П., Владыкин Р.Г. // Электрохимия. 2016. Т. 52. № 10. С. 1085; https://doi.org/10.7868/S0424857016100042
Kuhne M., Paolucci F., Popovic J., Ostrovsky P.M., Maier J., Smet J.H. // Nature Nanotech. 2017. V. 12. P. 895; https://doi.org/10.1038/nnano.2017.108
Rakhmanova O.R., Galashev A.E. // Rus. J. Phys. Chem. A. 2017. V. 91. № 5. P. 921; https://doi.org/10.1134/S003602441705020X
Галашев А.Е., Иваничкина К.А., Воробьев А.С., Рахманова О.Р. // ФТТ. 2017. Т. 59. № 6. С. 1218;
Galashev A.Y., Ivanichkina K.A. // Phys. Lett. A. 2017. V. 381. P. 3079; https://doi.org/10.1016/j.physleta.2017.07.040
Галашев А.Е., Иваничкина К.А. // ЖФХ. 2017. V. 91. № 12. С. 125; https://doi.org/10.1134/S003602441712007X
Sitinamaluwa H., Nerkar J., Wang M., Zhang S., Yan C. // RSC Adv. 2017. V. 7. № 22. P. 13487; https://doi.org/10.1039/C7RA01399J
Tritsaris G.A., Kaxiras E., Meng S., Wang E. // Nano Lett. 2013. V. 13. № 5. P. 2258; https://doi.org/10.1021/nl400830u
Quhe R., Yuan Y., Zheng J. et al. // Sci. Rep. 2014. V. 4. P. 5476; https://doi.org/10.1038/srep05476
Cahangirov S., Ozcelik V.O., Xian L. et al. // Phys. Rev. B. 2014. V. 90. № 3. P. 035448; https://doi.org/10.1103/PhysRevB.90.035448
Chen L., Li H., Feng B. et al. // Phys. Rev. Lett. 2013. V. 110. № 8. P. 085504; https://doi.org/10.1103/PhysRevLett.110.085504
Echigoya J., Enoki H., Satoh T. et al. // Appl. Surf. Sci. 1992. V. 56. № 8. P. 463; https://doi.org/10.1016/0169-4332(92)90272-Y
Zhang J., Liu C., Shu Y., Fan J. // Appl. Surf. Sci. 2012. V. 261. P. 690; https://doi.org/10.1016/j.apsusc.2012.08.082
Vaz C.A.F., Steinmuller S.J., Moutafis C., Bland J.A.C., Babkevich A.Y. // Surf. Sci. 2007. V. 601. P. 1377; https://doi.org/10.1016/j.susc.2007.01.001
Tersoff J. // Phys. Rev. B. 1988. V. 38. № 14. P. 9902; https://doi.org/10.1103/PhysRevB.38.9902
Tersoff J. // Ibid. 1994. V. 49. № 23. P. 16349; https://doi.org/10.1103/PhysRevB.49.16349
Foiles S.M., Baskes M.I., Daw M.S. // Ibid. 1986. V. 33. № 12. P. 7983; https://doi.org/10.1103/PhysRevB.33.7983
Yu R., Zhai P., Li G., Liu L. // J. Electron. Mater. 2012. V. 41. № 6. P. 1465; https://doi.org/10.1007/s11664-012-1916-x
Das S.K., Roy D., Sengupta S. // J. Phys. F: Metal. Phys. 1977. V. 7. № 1. P. 5; https://doi.org/10.1088/0305-4608/7/1/011
Fang T.-E., Wu J.-H. // Comp. Mater. Sci. 2008. V. 43. № 4. P. 785; https://doi.org/10.1016/j.commatsci.2008.01.066
Pan Y., Zhang L., Huang L. et al. // Small. 2014. V. 10. № 11. 2215; https://doi.org/10.1002/smll.201303698
Berdiyorov G.R., Bahlouli H., Peeters F.M. // J. Appl. Phys. 2015. V. 117. № 22. P. 225101; https://doi.org/10.1063/1.4921877
Kawahara K., Shirasawa T., Arafune R. et al. // Surf. Sci. 2014. V. 623. P. 25; https://doi.org/10.1016/j.susc.2013.12.013
Berdiyorov G.R., Neek-Amal M., Peeters F.M., van Duin A.C.T. // Phys. Rev. B. 2014. V. 89. № 2. P. 024107; https://doi.org/10.1103/PhysRevB.89.024107
Galashev A.Y., Ivanichkina K.A. // J. Electrochem. Soc. 2018. V. 165. № 9. P. A1788; https://doi.org/10.1149/2.0751809jes
Plimpton S. // J. Comp. Phys. 1995. V. 117. № 1. P. 1; https://doi.org/10.1006/jcph.1995.1039
Галашев А.Е. // Физика металлов и металловедение. 2016. Т. 117. № 3. С. 258; https://doi.org/10.7868/S0015323016030050
Roman R.E., Cranford S.W. // Comp. Mater. Sci. 2014. V. 82. P. 50; https://doi.org/10.1016/j.commatsci.2013.09.030
Neubeck S., Freitag F., Yang R., Novoselov K.S. // Phys. Stat. Sol. B. 2010. V. 247. P. 2904; https://doi.org/10.1002/pssb.201000186
Tapaszto L., Dobrik G., Nemes-Incze P., Vertesy G., Lambin Ph., Biró L.P. // Phys. Rev. B. 2008. V. 78. P. 233407; https://doi.org/10.1103/PhysRevB.78.233407
Kowaki Y., Harada A., Shimojo F., Hoshino K. // J. Phys. Condens. Matter. 2009. V. 21. P. 064202; https://doi.org/10.1088/0953-8984/21/6/064202
Галашев А.Е., Рахманова О.Р. // УФН. 2014. Т. 184. С. 1045;
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика


