Химическая физика, 2020, T. 39, № 9, стр. 63-70
Микроструктура металла в откольных пластинах
С. Н. Буравова 1, *, Е. В. Петров 1
1 Институт структурной макрокинетики и проблем материаловедения им. А.Г. Мержанова,
Российской академии наук
Черноголовка, Россия
* E-mail: svburavova@yandex.ru
Поступила в редакцию 11.07.2019
После доработки 27.09.2019
Принята к публикации 21.10.2019
Аннотация
Ультразвуковые колебания откольных пластин с частотой в несколько МГц протекают в форме стоячей волны. Реверберация пластины относится к категории ультразвука с достаточно большими амплитудами колебаний. Периодическая смена циклов сжатие–растяжение, характерная для процессов осцилляции, приводит к локализации пластической деформации в узлах стоячей волны. Следствием процесса локализации деформации является эффект самозалечивания: элементы внедрения и ультрадисперсные частицы легирующей фазы мигрируют из матричного материала в зону растущей откольной повреждаемости. Микроструктура металла в полосах локализованной деформации состоит из сильнодеформированного бесструктурного материала, содержащего чашечные очаги разрушения размером 1–3 мкм с большим количеством микропор. Физико-химические процессы, такие как фрагментация, растворение частиц легирующей фазы, карбидизация, ответственны за формирование микроструктуры полос локализации.
ВВЕДЕНИЕ
Практически во всех взрывных экспериментах наблюдается образование полос локализованной деформации (ПЛД) – предвестников разрушения. Как правило, возникающие осколки ограничены такими полосами. Интенсивное экспериментальное изучение процессов импульсного воздействия на материал, которые сопровождаются образованием ПЛД, нашло отражение в многочисленных обзорах, монографиях и статьях. Несмотря на многочисленные исследования, не удавалось найти корреляцию между образованием ПЛД, физико-механическими свойствами материала и условиями нагружения. В рамках общепринятой термомеханической модели локализации деформации Зенера–Холомона, основанной на механизме потери устойчивости пластического течения в результате перехода работы деформации в тепло, получить ответ на поставленные вопросы невозможно. В настоящее время, как утверждают авторы работ [1, 2], нет представлений о механизме зарождения и развития процесса локализации деформации, отсутствует общее представление о зависимости критических параметров начала локализации от исходных структур. Роль исходной структуры в инициировании процесса локализации признана незначительной [3].
Локализация деформации для всех исследованных образцов в экспериментах по коллапсу толстостенных полых цилиндров характеризуется образованием симметричной системы трещин вблизи внутренней полости образца. Медь и фторопласт, имеющие качественно различные структуры, образуют схожую систему трещин вблизи центральной части образца. В работе [4] впервые была обоснована откольная природа образования полос локализации. В условиях взрывного (динамического) нагружения ПЛД возникают в зоне интерференции волн разгрузки, где растягивающие напряжения по величине не превышают динамическую прочность и материал после деформирования сохраняет свою сплошность. По своей сути, полосы являются незавершенными откольными трещинами (откол – динамическая форма разрушения, образующегося в зонах интерференции волн разгрузки). Таким образом, геометрическая форма образца определяет возникновение ПЛД. Расположение свободных поверхностей, источников волн разгрузки, определяет место зарождения ПЛД в образцах при динамическом нагружении. Геометрический фактор расположения свободных поверхностей является инструментом, позволяющим управлять процессом локализации пластической деформации. Многочисленными экспериментами [5] была доказана откольная природа полос локализации деформации.
Следствием откольной природы образования ПЛД является осцилляция (реверберация) всего образца. Это неожиданный результат для процесса локализации деформации, который требует обоснования. Изучение структуры материала в откольных пластинах, для которых явление реверберации – известный факт, позволит судить о процессах, влияющих на изменение структуры материала в ПЛД. Цель работы – изучение микроструктуры в откольных пластинах и физико-химических процессов, сопровождающих формирование этой структуры.
Особенности реверберации откольных пластин
Образование откольной пластины в классической схеме ударно-взрывного нагружения и ее отделение от образца обусловлены взаимодействием торцевых волн разгрузки, в зоне интерференции которой возникают сильные растягивающие напряжения, равные или превышающие по величине динамическую (откольную) прочность материала. Часть образца перед откольной трещиной отделяется, образуя откольную пластину, или, как часто ее называют, откольную тарелочку. При отрыве от образца в тарелочке сохраняется значительная доля импульса сжатия, близкая по величине к откольной прочности материала σs, что позволяет пластине без действия внешних сил совершать колебательные движения в полете. Факт осцилляции откольной тарелочки хорошо известен [6]. Как отмечается в работе [7], в образце может возникать столько откольных пластин, во сколько раз амплитуда входящей ударной волны превосходит откольную прочность материала.
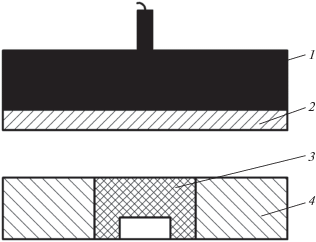
Рисунок 1 демонстрирует схему эксперимента, позволяющую сохранить тарелочку в образце. В момент удара на границе контакта возникают две ударные волны, выход которых на свободные торцевые поверхности образца и пластины-ударника порождает две центрированные волны разгрузки. При этом одна из торцевых граней теряет скорость, а другая приобретает скорость, равную по величине удвоенной массовой скорости. Стаканообразная форма образца препятствует выходу откольной трещины на боковую поверхность. В результате между сформировавшейся откольной тарелочкой и образцом образуется щель и отрыв ее от образца предотвращается.
Рис. 1.
Схема эксперимента, моделирующего образование торцевой откольной повреждаемости: 1 – взрывчатое вещество, разгоняющее пластину-ударник; 2 – пластина-ударник; 3 – образец в форме короткого толстостенного стакана (такая форма позволяет сохранить откольную пластину, образующуюся в процессе удара пластины); 4 – обойма, удерживающая образец от разрушения.
При импульсном нагружении процессы взаимодействия волн (разгрузки или сжатия) между собой и с гранями образца с неизбежностью приводят к его деформированию в результате колебательного движения среды. Действительно, откольный характер повреждения требует наличия по крайней мере двух свободных поверхностей – источников волн растяжения (разгрузки). Интерференция волн на свободных гранях образца, т.е. сложение падающей волны со своей отраженной волной противоположного знака, приводит к образованию стоячей волны и осцилляции пластины [8, 9], что сопровождается изменением знака направления скорости движения граней (волна сжатия преобразуется в волну разгрузки и наоборот). Свободные грани тарелочки, где напряжение всегда равно нулю, являются пучностью стоячей волны. Узлы стоячих волн образуются в местах взаимодействия (интерференции) отраженных от противоположных граней волн. Частицы в узлах неподвижны. Расстояние между двумя соседними узлами или пучностями равно λ/2 – половине длины волны, равной толщине тарелочки. В симметричной стоячей волне частицы среды то приближаются с двух сторон к узлу, то от него удаляются. В результате колебательного движения среды в узлах возникает наиболее резкое изменение плотности и напряжения. Интерференция встречных волн, отраженных от разных граней, создает внутри образца узкую зону (равную ширине падающего импульса), где периодически происходит смена циклов сжатие–растяжение [10].
Теория стоячих волн хорошо известна [8, 9, 11]. Стоячие волны формируются в волноводах многих ультразвуковых приборов. Образование полос адиабатического сдвига в экспериментах на установках Гопкинсона объясняется реверберацией [12]. Колебательная энергия частиц в стоячей волне, заключенных между пучностью, где напряжение равно нулю, и ближайшим узлом, где массовая скорость равна нулю, сохраняется на одной четверти длины стоячей волны. Эта особенность последней приводит к длительной деформации образца после прохождения ударной волны через образец.
Волны Лэмба осуществляют колебательное движение среды. Частота колебаний γ = c0/2δ находится в ультразвуковом диапазоне частот и зависит от толщины тарелочки δ и скорости звука c0. Скорость движения тарелочки в случае ее отделения от образца в 2 раза превышает массовую скорость 2u0 за плоской ударной волной, а каждая следующая тарелочка приобретает меньшую на величину 2us скорость полета, где us – массовая скорость, соответствующая динамической прочности σs. Скорость вибрации свободных граней для новых тарелочек не остается прежней и меняется по величине от ~2us до 0. Особенностью стоячих волн является образование замкнутых областей размером λ/4 (между узлом и пучностью), в которых отсутствует обмен энергией через узловые точки. В отличие от плоской бегущей волны энергия стоячей волны не распространяется. Энергией обладают лишь частицы, колеблющиеся между узлами [9]. Осцилляция продолжается без действия внешних сил, что приводит к длительному деформированию образца.
В отличие от классического ультразвука, генерируемого источниками звуковых волн, узлы стоячих волн при взрывных нагрузках, возникающие в зоне интерференции волн, отраженных от граней откольной тарелочки, имеют конечные размеры. Ширина зоны интерференции волн мала и равна 2bs0, где s0 = u0/c0 – отношение массовой скорости к скорости звука, b – коэффициент в линейной зависимости скорости распространения ударной волны от массовой скорости [13].
Затухание стоячих волн (реверберация)
Процесс осцилляции напряжений в откольных тарелочках продолжается до тех пор, пока волны сжатия и растяжения не затухнут в результате необратимых потерь. Свойство твердых тел превращать механическую энергию в тепло в процессе деформации принято рассматривать как наличие внутреннего трения. Поглощение энергии связано с рассеянием ультразвуковых колебаний на неоднородностях структуры. Диссипативные процессы приводят к необратимому превращению механической энергии в тепло.
Можно оценить время затухания волн, используя геометрическую интерпретацию законов сохранения. Из геометрического представления законов сохранения [14] следует, что энергия ударного нагружения, переходящая в тепло, равна площади на P–V-диаграмме между прямой, соединяющей исходное и конечное состояния (прямая Рэлея), и кривой изэнтропического сжатия. Согласно работе [15], удельная потеря энергии равна e = (1/3)ρ0$c_{0}^{2}$bε3, где ρ0 – плотность металла, ε = s0 = u0/c0 – степень деформации. Коэффициент энергии 2α характеризует долю энергии, перешедшей в тепло, к полной энергии единицы массы:
При выводе формулы (1) авторы работы [15] заменили изэнтропу адиабатой. Более точное значение коэффициента затухания амплитуды с учетом особенности изэнтропы при низких импульсных нагрузках получено в работе [12]. Для идеальной упругопластической среды (модуль упрочнения равен нулю) удельная потеря энергии e зависит от динамического предела текучести σy и степени деформации, соответствующей пределу упругости Гюгонио σG: e = 2σy(ε – εG)/3ρ0. Учитывая, что удельная энергия ударно-сжатого вещества пропорциональна квадрату массовой скорости, а локализация деформации возникает при напряжениях чуть ниже откольной прочности σs, выражение для доли диссипативной энергии, перешедшей в тепло [16], принимает вид
(2)
$2{{\alpha }_{s}} \approx \frac{{{{\sigma }_{y}}\left( {{{\sigma }_{s}} - {{\sigma }_{G}}} \right)}}{{3\sigma _{s}^{2}}}.$В табл. 1 приведены исходные данные, используемые для расчета коэффициента затухания стоячей волны, где С – продольная скорость звука. Коэффициент затухания стоячей волны равен доле энергии, переходящей в тепло, деленной на период колебания Т, а коэффициент затухания амплитуды стоячей волны – половине энергетического коэффициента затухания.
Таблица 1.
| Металл | ρ0, кг/м3 |
σG, ГПа |
σу, ГПа |
σs, ГПа | С, км/с |
с0, км/с |
b, км/с |
us, м/с |
|---|---|---|---|---|---|---|---|---|
| Al | 2780 | 0.6 | 0.29 | 1.22 | 6.36 | 5.33 | 1.36 | 80.7 |
| Cu | 8800 | 0.16 | ~0.08 | 1.64 | 4.729 | 3.90 | 1.52 | 46.9 |
| Ti | 4450 | 2.0 | 0.92 | 3.5 | 6.15 | 5.11 | 2.00 | 145.0 |
| Fe | 7900 | 1.4 | 0.82 | 4.25 | 5.77 | 4.63 | 1.33 | 112.6 |
Интенсивность ультразвуковых волн принято оценивать по максимальной амплитуде колебания в пучностях стоячей волны l = 2usT/2 = usT. Согласно работе [17], в стоячей волне максимальное смещение пульсирующей грани (пучности) для классической ультразвуковой волны составляет несколько десятков микрон. К ультразвуку относятся колебания с большой амплитудой: 50–100 мкм. Ультразвуковые колебания с частотой 1–2 МГц приводят в металлах к необратимым явлениям (изменение структуры материала, упрочнение, повреждаемость). Как отмечает автор работы [17], знакопеременные напряжения вызывают движение дефектов (дислокаций). В отличие от обратимых явлений, когда дислокации колеблются около своих точек закрепления (атомы примесей, узлы дислокационной сетки), при необратимом характере деформации дислокации срываются с точек закрепления и начинают поступательное движение в материале, что приводит к значительному увеличению коэффициентов затухания. Как видно из табл. 2, осцилляцию титановой и стальной откольных тарелочек можно отнести к ультразвуку с большой величиной амплитуды колебания.
Таблица 2.
Характеристики колебательного движения в откольных пластинах
| Металл | δ, мм | T, мкс | γ, МГц | l, мкм | 2αs, 1/мкс | 2αG, 1/мкс | N | td, мкс |
|---|---|---|---|---|---|---|---|---|
| Al | 1.800 | 0.566 | 1.77 | 45.6 | 0.0805 | 0.0069 | 25 | 40 |
| Cu | 1.644 | 0.695 | 1.44 | 32.6 | 0.029 | 0.008 | 67 | 46 |
| Ti | 1.701 | 0.553 | 1.80 | 80.2 | 0.075 | 0.0189 | 27 | 72 |
| Fe | 1.800 | 0.624 | 1.60 | 69.9 | 0.086 | 0.0108 | 23 | 48 |
Примечание: δ – толщина откольной пластины, Т – период, γ – частота ультразвукового колебания, l – максимальное смещение грани тарелочки, 2αs [12] и 2αG [15] – доли энергии, переходящей в тепло, N – число колебаний до затухания амплитуды в е раз, td – время деформирования в области пластической деформации.
Другой характеристикой реверберации является число колебаний N, совершаемых образцом до того, как амплитуда уменьшится в е = 2.718 раз. Затухание амплитуды стоячей волны описывается экспоненциальным законом убывания ее амплитуды: ${{{{\sigma }_{s}}} \mathord{\left/ {\vphantom {{{{\sigma }_{s}}} \sigma }} \right. \kern-0em} \sigma } = \exp {{\alpha }_{s}}T$ = $\exp {{\alpha }_{s}}N = e.$ Откуда число колебаний, необходимое для затухания амплитуды колебания в е раз, равно $N = {1 \mathord{\left/ {\vphantom {1 {{{\alpha }_{s}}}}} \right. \kern-0em} {{{\alpha }_{s}}}}.$ Коэффициенты затухания стоячей волны, рассчитанные по формулам (1) и (2), различаются почти на порядок. В табл. 2 число колебаний N и время затухания амплитуды td оценивались по коэффициентам αs на основе данных из работы [12].
Таким образом, анализ волновой картины образования откольной пластины и особенностей распространения волн в ней совместно с литературными данными показал, что осцилляция откольных тарелочек протекает в форме стоячих волн, которые создают необходимые условия для локализации пластической деформации, поскольку напряжение не превышает откольной прочности материала. Ультразвуковые колебания в откольных пластинах относятся к достаточно сильным осцилляциям и сопровождаются знакопеременной деформацией с периодической сменой циклов сжатие–разгрузка.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В соответствии с откольной природой возникновения полос локализации деформации в работах [4, 5, 18] показано, что при импульсном нагружении пóлосы локализованной деформации возникают в зоне интерференции волн разгрузки, где высокоскоростное растяжение не превышает динамической прочности материала. При взрывном нагружении процесс локализации пластической деформации является следствием осцилляции, которая возникает в образцах ограниченных размеров в результате отражения волн от свободных граней образца и взаимодействия (интерференции) их между собой.
В работе использовалась классическая схема ударного нагружения пластины [6], приведенная на рис. 1. Алюминиевая пластина-ударник диаметром 60 мм и толщиной 2 мм разгонялась до скорости в 1 км/с накладным зарядом гексогена насыпной плотности 0.95 г/см3, скорость детонации которого составляла 5.8 км/с. Образец в форме стакана позволял удерживать откольную тарелочку в образце. Давление, создаваемое ударной нагрузкой в образцах, было порядка 10–15 ГПа, что в несколько раз превышает откольную прочность исследуемых материалов. В качестве материала образцов изучали медный сплав М1 и сплав титана Ti6Al4V. Исследование структуры сохраненных после взрывной обработки образцов проводилось с помощью оптического микроскопа Neophot-30, сканирующего электронного микроскопа LEO 1450 и электронного микроскопа сверхвысокого разрешения Zeiss Ultra plus.
Микроструктура ПЛД в медной откольной пластине
Медь не испытывает фазовых превращений. Ее поведение при взрывном нагружении является классически гидродинамическим, поскольку практически отсутствует упругий предвестник. Длительный отжиг монокристалла меди при температуре 900°С позволил обнаружить предел упругости с амплитудой порядка 0.16 ГПа [6]. Преимущественным механизмом пластической деформации в поликристаллической меди считается скольжение. Двойникование в процессе высокоскоростной пластической деформации играет второстепенную роль. Своеобразное поведение меди проявляется в отсутствии ПЛД при динамическом кручении в процессе высокоскоростной деформации, поэтому медную пластину предварительно упрочняли ударной волной с давлением в 50 ГПа [19]. Взрывное раздутие трубчатого образца меди также не привело к образованию ПЛД [20].
На рис. 2а приведен общий вид откольной пластины в медном образце. Процесс локализации пластической деформации проявляется в образовании двух полос откольной повреждаемости преимущественно в виде откольных микротрещин, переходящих местами в ПЛД. Толщина Cu-тарелочки равна δ = 1.644 мм. Среди изученных металлов медь обладает наименьшим коэффициентом затухания. Видимо, длительная реверберация в мегагерцевом диапазоне колебаний приводит к охрупчиванию меди и, как следствие, преимущественной повреждаемости в форме откольной трещины.
Рис. 2.
Микрофотографии образца из меди: a – общий вид откольной тарелочки; б – микроструктура полосы локализации в откольной тарелочке.

Микроструктура в ПЛД (рис. 2б) характеризуется сильнодеформированным материалом, содержащим большое количество очагов разрушения, представляющих собой вскрытые микропустоты классического ямочного типа размером 1–3 мкм. Во многих очагах обнаруживаются микропоры. Такие же микропоры наблюдаются при квазистатическом растяжении в нагруженных твердых телах [21]. При сравнении микроструктур полос локализации деформации в откольных тарелочках и возникающих в области перехода откольной трещины в полосу локализации [22] обнаруживается их идентичность. Образование в зоне интерференции волн разгрузки очагов разрушения микронного размера предполагает, что мелкие очаги в поликристаллическом материале зарождаются на дислокациях, которые возникают в процессе динамического растяжения, в то время как более крупные очаги разрушения возникают на врожденных неоднородностях, всегда присутствующих в исходном материале. Область перехода откольной трещины в ПЛД содержит огромное количество скоплений дислокаций, которое существенно превышает число скоплений дислокаций, созданных ударной волной [22].
Согласно работе [23], образование микропор в условиях высокоскоростного растяжения происходит за счет конденсации вакансий, избыток которых при динамических нагрузках вызван совместным действием ударной волны и последующей деформации. Авторы работы [23] высказали мнение, что структура деформируемого материала в медном образце, содержащая скопление дислокаций, может быть аморфной.
Микроструктура ПЛД в титановой откольной пластине
Рисунок 3а демонстрирует общий вид откольной пластины в титановом образце. Множество ПЛД, как видно по фотографии шлифа, свидетельствует об образовании дополнительных гармоник стоячей волны, что подтверждает наличие осцилляции образца при формировании ПЛД. Известно, что в условиях реверберации, кроме волны основного тона с λ0/4 = δ/2, возникают сопутствующие гармоники с длинами λn/4 = δ/2n, где λn – длина волны, n – нечетное число [8]. Толщина Ti-тарелочки равна δ = 1.701 мм. Область, где возникла система ПЛД в откольной пластине, занимает 0.508 мм и смещена в сторону откольной трещины. Микроструктура ПЛД в титановом сплаве, приведенная на рис. 3б, состоит из сильно деформированной пластичной β-фазы, обнаружить границы зерен в которой не представляется возможным. Большое количество зародышевых очагов разрушения классического чашечного вида с размером от 200 нм до 3.8 мкм, содержат микропоры, размер которых изменяется от 50 до 300 нм. Такая структура материала характерна для многих изученных металлов (медь, сталь, алюминий) при напряжениях, близких к откольной прочности материала [18]. Осцилляция напряжения в зоне интерференции волн приводит к появлению в структуре фрагментированного металла: раздробленных, деформированных осколков материала, размер которых изменяется в широком диапазоне. Как следует из табл. 2, откольная пластина из титанового сплава характеризуется наибольшей амплитудой смещения пульсирующей грани (пучности) в стоячей волне.
Рис. 3.
Микрофотографии образца из титана: a – общий вид откольной тарелочки; б – микроструктура полосы локализации в образце.

Исходный сплав титана Ti6Al4V – двухфазный: пластины более темной β-фазы оторочены светлой α-фазой, и характеризуется равномерным распределением фаз по всему образцу. Однако вблизи поврежденного металла фазовый состав изменяется.
Анализ структуры ПЛД (рис. 4) показывает, что светлая, более твердая α-фаза раздроблена и в мелкодисперсной форме собирается на местах поврежденного металла, накапливается у краев откольных трещин, создавая видимость белой полосы. Более темные области рядом с откольной повреждаемостью на рис. 4 обеднены частицами твердой α-фазы, что свидетельствует о миграции ультратонких частиц из матричного материала к местам нарушения сплошности. В результате сегрегации α-фазы в зоне интерференции волн происходит перераспределение фазового состава.
Дрейф частиц упрочняющей фазы к местам поврежденного металла наблюдался при квазистатическом холодном деформировании [24]. Авторы [24] отмечают, что активное развитие процесса массопереноса совпадает с образованием областей “некристаллографического” сдвига, что сопровождается генерацией кристаллических дефектов. Часто сегрегация интерметаллидов отмечает наличие таких полос сдвига.
Рис. 4.
Сегрегация ультратонких частиц α-фазы на местах откольной повреждаемости в двухфазном титановом сплаве.
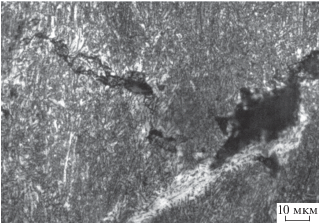
Ранее явление массопереноса ультратонких частиц упрочняющей фазы наблюдалось для дисперсно-упрочненного сплава алюминия [13] и было названо эффектом самозалечивания. Эффект массопереноса частиц, сопровождающий образование ПЛД, есть следствие процесса локализации деформации и наблюдается во многих материалах. В сталях с феррито-перлитной структурой обнаружена миграция углерода [10]. С помощью энерго-дисперсионного анализа стального образца на содержание углерода вблизи области откольной повреждаемости обнаружен слой толщиной 10–40 мкм, обедненный углеродом. В медном образце эффект самозалечивания [23] проявляется в образовании зародышей оксидов на фрагментах меди в ПЛД. Предполагается, что в процессе высокоскоростной деформации кислород, растворенный в материале при его изготовлении, мигрирует к образующейся области поврежденного материала.
Анализ проблемы аномального массопереноса при импульсных нагрузках проведен в работе [25] с учетом сведений о физико-химических процессах, сопровождающих импульсное нагружение. Показано, что массоперенос атомов и частиц легирующей фазы из матричного материала к местам откольной повреждаемости является неотъемлемым свойством процесса локализации деформации. Перераспределение энергии между ударной волной и стоячими волнами, в силу особенностей колебания среды в стоячих волнах, приводит к длительному деформированию образца за счет осцилляции напряжения в стоячих волнах. Значительное увеличение длительности деформирования по сравнению с начальным импульсом и наличие свободного объема, периодически возникающего в ПЛД в результате осцилляции, являются факторами, способствующими увеличению подвижности атомов и миграции дисперсных частиц. Аномальность массопереноса появляется, когда расстояния, на которые перемещаются частицы (атомы, примесь, тонкодисперсные частицы упрочняющей фазы и пр.), определяются длительностью импульсного нагружения, а не временем импульсного деформирования образца. Учет времени затухания стоячих волн снимает проблему аномальности массопереноса при импульсном нагружении [25].
ЗАКЛЮЧЕНИЕ
Реверберация, сопровождающая движение откольной тарелочки, представляет собой затухающую стоячую волну, в узлах которой зарождаются и эволюционируют полосы локализации деформации. Периодическая смена напряжений сжатия и растяжения приводит к фрагментации частиц, растворению упрочняющей фазы, карбидизации перлита в сталях, окислению фрагментов, ускоренному массопереносу атомов внедрения, замещения и ультратонких частиц упрочняющей фазы из матричного материала к местам откольной повреждаемости, а также к изменению фазового состава в ПЛД, что и определяет формирование структуры внутри полос. Особенность стоячей волны – сохранять энергию на участках волны между узлом и пучностью и не обмениваться ею с соседним материалом – обеспечивает длительный процесс деформирования тарелочки после ее отделения от образца.
Список литературы
Нестеренко В.Ф., Бондарь М.П. // Физика горения и взрыва. 1994. № 4. С. 99.
Бондарь М.П. // Физическая мезомеханика. 2000. Т. 3. № 6. С. 75.
Бондарь М.П., Первухина О.Л. // Физика горения и взрыва. 2000. № 2. С. 110.
Беликова А.Ф., Буравова С.Н., Гордополов Ю.А. // ЖТФ. 2013. Т. 83. № 2. С. 153.
Беликова А.Ф., Буравова С.Н., Петров Е.В. // ЖТФ. 2013. Т. 83. № 8. С. 68.
Канель Г.И., Разоренов С.В., Уткин А.В., Фортов В.Е. Ударно-волновые явления в конденсированных средах. М.: “Янус-К”, 1996.
Rinehart J.S., Pearson J. Behavior of Metals under Impulsive Loads. Cleveland, Ohio: Amer. Soc. Metals, 1954.
Викторов И.А. Физические основы применения ультразвуковых волн Рэлея и Лэмба в технике. М.: Наука, 1966.
Горелик Г.С. Колебания и волны. Введение в акустику, радиофизику и оптику. М.: Физматлит, 1959.
Буравова С.Н., Петров Е.В., Алымов М.И. // ДАН. 2016. Т. 469. № 1. С. 34.
Агранат Б.А., Башкиров В.И., Китайгородский Ю.И., Хавский Н.Н. Ультразвуковая технология. М.: Металлургия, 1974.
Степанов Г.В. Упруго-пластическая деформация материалов под действием импульсных нагрузок. Киев: Наук. думка, 1979.
Буравова С.Н. // ЖТФ. 2017. Т. 87. № 10. С. 1502.
Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М.: Физматгиз, 1963.
Grady D.E., Asay J.R. // J. Appl. Phys. 1982. V. 53. P. 7350.
Глушак Б.Л., Куропатенко, В.Ф., Новиков С.А. Исследование прочности материалов при динамических нагрузках. Новосибирск: Наука, 1992.
Кулемин А.В. Ультразвук и диффузия в металлах. М.: Металлургия, 1978.
Буравова С.Н. Этюды на тему локализации динамической деформации: откольная модель локализации пластической деформации. Saarbrücken: Palmarium Acad. Publ., 2014.
Andrade U., Meyers M.A., Vecchio K.S., Chokshi A.H. // Acta Metall. Mater. 1994. V. 42. P. 3183.
Могилевский М.Л., Булгаков В.В., Кормачев А.Д. // Физика горения и взрыва. 1994. № 3. С. 96.
Бетехтин В.И., Кадомцев А.Г. // ФТТ. 2005. Т. 47. № 5. С. 801.
Буравова С.Н., Петров Е.В., Щукин А.С. // Физика горения и взрыва. 2016. Т. 52. № 5. С. 131.
Tang N.-Y., Niessen P., Pick R.J., Worswick M.J. // Mater. Sci. Eng., A. 1991. V. 131. P. 153.
Кузнецов А.Р., Сагарадзе В.В. // Физика металлов и металловедение. 2002. Т. 93. № 5. С. 13.
Буравова С.Н., Петров Е.В. // Хим. физика. 2018. Т. 37. № 2. С. 47.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика


