Химическая физика, 2021, T. 40, № 1, стр. 79-89
Концепция хаотического искажения когерентных структур для интерпретации турбулентности. 1. Влияние неупорядоченных возмущений
А. Ф. Киселёв 1, И. В. Лебедь 2, *
1 Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Жуковский, Россия
2 Институт прикладной механики Российской академии наук
Москва, Россия
* E-mail: lebed-ivl@yandex.ru
Поступила в редакцию 05.02.2020
После доработки 13.03.2020
Принята к публикации 20.03.2020
Аннотация
Уравнения многомоментной гидродинамики привлечены для численного моделирования хаотического искажения регулярных режимов в задаче обтекания покоящейся твердой сферы. Исследуется влияние неупорядоченных возмущений, возникающих в среде за счет внешнего воздействия. После пересечения критического значения числа Рейнольдса стационарное решение уравнений многомоментной гидродинамики теряет устойчивость. Каждое отклонение от потерявшего устойчивость стационарного решения начинает вести себя во времени сугубо индивидуально. Перестает существовать некоторое среднее решение, пригодное для интерпретации всех изначально близких неустойчивых решений. Ансамбль Гиббса распадается. Потеря устойчивости сопровождается качественным изменением в поведении неупорядоченных возмущений. Независимость в их поведении исчезает. Законы сохранения вынуждают неупорядоченные возмущения подстраивать свое поведение во времени и в пространстве под поведение гидродинамических величин.
ВВЕДЕНИЕ
Полуэмпирический подход к расчету турбулентности базируется на предположении О. Рейнолдьса о том, что турбулентное движение строго описывается уравнениями Навье–Стокса. В этом далеко не очевидном предположении заключается основная идея полуэмпирического подхода. Далее гидродинамические величины представляются в виде линейной комбинации некоторой осредненной и пульсационной составляющих. Дифференциальное уравнение сохранения импульса для осредненного движения названо усредненным по Рейнольдсу уравнением Навье–Стокса (RANS) [1]. Идеология осреднения движения получила свое дальнейшее развитие в рамках современного метода моделирования крупных вихрей (LES). В методе LES осреднение поля течения (фильтрация) проводится на некотором характерном масштабе, отождествляемом обычно с размером расчетной сетки. Таким образом, уравнения LES способны сохранить вихревые структуры крупного размера (когерентные структуры [2]), теряя мелкие детали течения. Для приведения уравнений RANS и LES к пригодному для интегрирования виду необходимо сформировать дополнительные эмпирические, а иногда и просто интуитивные модельные представления, позволяющие провести замыкание этих уравнений.
Относительная простота приближенных методов интегрирования уравнений RANS и LES позволила использовать их при попытке воспроизвести турбулентные процессы, происходящие в окружающей среде, на промышленных предприятиях и в экспериментальных установках. Зачастую оказывается, что результаты расчетов имеют значительные количественные и качественные расхождения с данными эксперимента. Несмотря на это, полуэмпирические уравнения RANS и LES по-прежнему широко используются для решения практических задач. Необходимым условием корректности приближенных полуэмпирических методов является совпадение результатов RANS- и LES-расчетов с результатами прямого численного интегрирования уравнений Навье–Стокса. Прямое численное интегрирование есть наиболее точный способ моделирования наблюдаемых явлений, простых и сложных.
Эксперимент [3] дает отчетливое представление о механизме перехода от устойчивого состояния среды к турбулентности при обтекании твердой сферы. В соответствии с [3] после достижения некоторого критического значения числа Рейнольдса $Re_{2}^{*}$ течение теряет свою устойчивость. При $Re \geqslant Re_{2}^{*}$ в следе за сферой появляется дорожка вихревых петель. Периферия зоны закручивания периодически отрывается от ее ядра и устремляется вниз по потоку в форме вихревой петли. Увеличение $Re$ сопровождается появлением первых элементов хаотичности как в зоне закручивания, так и на дорожке вихревых петель. По мере роста $Re$ хаотические искажения увеличиваются, структура зоны закручивания и вихревой петли становится менее отчетливой. При высоких $Re$ структура зоны закручивания и вихревой петли просматривается крайне слабо, ее все труднее отличить от хаотической структуры. Однако хаотические искажения не смогли полностью замаскировать вихревую дорожку. Таким образом, в соответствии с экспериментом [3] нарастание хаотичности происходит постепенно. Хаос накладывается на регулярную структуру зоны закручивания и вихревой дорожки.
Настоящая работа опирается на данные эксперимента [3]. Будем ориентироваться на то, что в соответствии с экспериментом зона закручивания и дорожка вихревых петель (периодическое вихревое испускание) являются регулярной составляющей турбулентного режима. Хаотические искажения, накладываясь на регулярную составляющую, постепенно скрывают ее. Однако хаотические искажения не в состоянии разрушить регулярную составляющую турбулентного режима.
Настоящая работа посвящена исследованию возникновения и развития турбулентности в задаче обтекания твердой сферы. Уравнения многомоментной гидродинамики привлечены для численного моделирования хаотического искажения регулярных режимов обтекания. В разд. 1 первой части исследования представлен первый регулярный режим, возникающий после потери устойчивости основным стационарным решением. В разд. 2 рассматриваются последствия перехода к неустойчивому режиму обтекания, сопровождающегося распадом ансамбля Гиббса. Уравнение сохранения импульса записывается с учетом вклада неупорядоченных возмущений скорости течения. Во второй части исследования выясняется причина роста неупорядоченных возмущений, приводящего к хаотическому искажению ламинарного течения в следе за сферой.
1. ПЕРВЫЙ НЕУСТОЙЧИВЫЙ РЕЖИМ ТЕЧЕНИЯ ЗА СФЕРОЙ
Предположение, именуемое гипотезой молекулярного хаоса, используется при выводе уравнения Больцмана. Уравнения классической гидродинамики следуют непосредственно из уравнения Больцмана, поэтому они неизбежно несут в себе погрешность, допущенную при выводе классического кинетического уравнения. Физический смысл погрешности, вносимой гипотезой молекулярного хаоса в уравнения гидродинамики, раскрывается в работах [4, 5]. Шестимерное фазовое пространство одной частицы способно разместить только три низших из общего бесконечного числа инвариантов бинарного соударения частиц. Однако строгого “выхода в гидродинамику” из 6-мерного фазового пространства не существует. Этот выход закрыт, поскольку первое уравнение иерархии Боголюбова–Борна–Грина–Кирквуда–Итона (ББГКИ) незамкнуто. Гипотеза молекулярного хаоса Больцмана замыкает первое уравнение иерархии. Таким образом, именно гипотеза Больцмана создает возможность приближенного “выхода в гидродинамику” из фазового пространства одной частицы. Именно гипотеза Больцмана позволяет выстроить гидродинамику на трех низших главных гидродинамических величинах, скажем, плотности, скорости и температуре. Все остальные гидродинамические величины выражаются через эти три главные. Именно гипотеза Больцмана исключает объективно существующие высшие главные гидродинамические величины из участия в формировании уравнений гидродинамики [5, гл. 3].
12-Мерное фазовое пространство двух частиц способно разместить полный набор инвариантов бинарного столкновения. Однако “выход в гидродинамику” из 12-мерного пространства тоже закрыт, поскольку второе уравнение иерархии ББГКИ также незамкнуто. В работе [6] предложено разделить все частицы газа на пáры. Две частицы названы парой в том случае, когда эти частицы либо движутся навстречу столкновению между собой, либо разлетаются после столкновения между собой. Далее предлагается пересчитывать пáры, а не отдельные частицы. Идея разделения частиц газа на пáры приводит к замкнутой системе двух линейных кинетических уравнений для парных функций распределения [7].
Уравнения для парных функций распределения являются основой для вывода уравнений многомоментной гидродинамики [5, гл. 5]. В работе [8] последние выстроены на семи главных гидродинамических величинах. Именно эти семь величин задают измеряемые моменты. Это плотность, скорость, температура, отвечающая тепловому движению центров масс пар, и температура, отвечающая относительному движению частиц в паре; одна из составляющих тензора вязких напряжений пропорциональна тензору скоростей деформаций (закон Ньютона), а другая является главной гидродинамической величиной; одна из составляющих теплового потока пропорциональна градиенту температуры (закон Фурье), а две другие являются главными гидродинамическими величинами. Проведенный анализ показывает, что уравнения многомоментной гидродинамики строго сводятся к уравнениям классической гидродинамики лишь в пределе слабого отклонения состояния среды от состояния термодинамического равновесия [9].
Парная функция распределения ${{f}_{p}}(t,x,G,{v})$ определена в работе [5, гл. 4]. В соответствии с основным свойством ${{f}_{p}}(t,x,G,{v})$ сохраняется во времени t вдоль траектории центра масс пары:
(1.1)
$\left( {\frac{\partial }{{\partial t}} + G\frac{\partial }{{\partial x}}} \right){{f}_{p}}(t,x,G,{v}) = 0.$В уравнении (1.1) x есть точка пространства, G – скорость центра масс частиц пары, v – модуль относительной скорости v частиц в паре. Таким образом, столкновения частиц не оказывают влияния на парную функцию распределения ${{f}_{p}}(t,x,G,{v}).$ Функция ${{f}_{p}}(t,x,G,{v})$ формируется под влиянием начальных и граничных условий задачи. Все главные гидродинамические величины являются моментами функции ${{f}_{p}}(t,x,G,{v}).$ Все неглавные гидродинамические величины определены в терминах главных гидродинамических величин в работе [5, гл. 5]. Таким образом, решение уравнения (1.1) позволяет построить распределения всех гидродинамических величин.
Рассмотрим пространство, заполненное термодинамически равновесным газом. Предположим, что твердая сфера радиуса a движется в газе с постоянной скоростью ${{U}_{0}}$ вдоль оси ${{Z}_{0}}$ неподвижной декартовой системы ${{X}_{0}}{{Y}_{0}}{{Z}_{0}}.$ Перейдем от системы ${{X}_{0}}{{Y}_{0}}{{Z}_{0}}$ к декартовой системе $XYZ$ с осями, параллельными ${{X}_{0}}{{Y}_{0}}{{Z}_{0}}$ и началом, совпадающим с центром движущейся сферы. В системе $XYZ$ сфера покоится, скорость набегающего потока газа на бесконечном расстоянии от сферы равна ${{U}_{0}}.$ Эта скорость совпадает с положительным направлением оси Z, поток стационарен.
В соответствии с основным свойством (1.1) в стационарной задаче парная функция не меняется вдоль прямой линии, параллельной вектору G. Функции ${{F}_{{xy}}} = {{G}_{x}}y - {{G}_{y}}x,$ ${{F}_{{zx}}} = {{G}_{z}}x - {{G}_{x}}z$ и ${{F}_{{zy}}} = {{G}_{z}}y - {{G}_{y}}z$ являются первыми интегралами уравнения (1.1) в стационарном случае. Функции ${{F}_{{xy}}},$ ${{F}_{{zy}}}$ и ${{F}_{{zx}}}$ названы в работе [10] траекторными инвариантами. Эти функции сохраняются по величине вдоль прямой линии, параллельной G. В настоящем исследовании рассмотрение ограничено течением газа вокруг сферы, которое инвариантно по отношению к повороту на произвольный угол вокруг оси Z. Образуем комбинации функций ${{F}_{{xy}}},$ ${{F}_{{zy}}}$ и ${{F}_{{zx}}},$ инвариантные по отношению к этому повороту:
(1.2)
$\begin{gathered} {{{\text{Ф}}}_{z}} = - ({{G}_{x}}{{F}_{{zx}}} + {{G}_{y}}{{F}_{{zy}}}), \\ {{{\text{Ф}}}_{r}} = {{\left( {F_{{xy}}^{2} + F_{{zx}}^{2} + F_{{zy}}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $Здесь x, y и z являются декартовыми координатами точки пространства x; $x = r\sin \theta \cos \varphi ,$ y = $ = r\sin \theta \sin \varphi ,$ $z = r\cos \theta ;$ $r,\,\,\theta $ и $\varphi $ – сферические координаты точки. Общий подход к решению уравнений многомоментной гидродинамики в терминах парных функций изложен в работах [10–12]. В соответствии с данными [10–12] в задаче с независящими от времени граничными условиями парная функция ${{f}_{p}}(t,x,G,{v})$ ищется в виде ряда произведений траекторных инвариантов из уравнения (1.2):
(1.3)
$\begin{gathered} {{f}_{p}}(t,x,G,{v}) = 4{\pi }{{\left( {\frac{M}{{2{\pi }k{{T}_{0}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\left( {\frac{\mu }{{2{\pi }k{{T}_{0}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\exp \left( { - \frac{{M{{G}^{2}}}}{{2k{{T}_{0}}}} - \frac{{\mu {{{v}}^{2}}}}{{2k{{T}_{0}}}}} \right)\sum\limits_{k = 0}^{ + \infty } {\sum\limits_{l = - \infty }^{ + \infty } {\sum\limits_{m = 0}^{ + \infty } {\sum\limits_{n = 0}^{ + \infty } {{{c}_{{klmn}}}} } } } \times \\ \times \,\,{{{\gamma }}^{k}}(G,{v}){\text{Ф}}_{r}^{l}{\text{Ф}}_{z}^{m}F_{{xy}}^{n}. \\ \end{gathered} $Пространственная зависимость функции ${{f}_{p}}(t,x,G,{v})$ в уравнении (1.3) контролируется траекторными инвариантами ${{F}_{{xy}}},$ ${{{\text{Ф}}}_{r}}$ и ${{{\text{Ф}}}_{z}},$ коэффициенты ${{c}_{{klmn}}} = {{c}_{{klmn}}}(t)$ не зависят от x. В (1.3) свойство ${{{\gamma }}^{k}}(G,{v})$ является инвариантом бинарного столкновения частиц, ${{T}_{0}}$ – температура невозмущенной среды, k – постоянная Больцмана, $M = 2m,$ $\mu = m{\text{/}}2,$ m – масса частицы. Функция ${{f}_{p}}(t,x,G,{v})$ из (1.3) используется для расчета распределений гидродинамических величин, главных и неглавных [5, гл. 5].
Подстановка рассчитанныx по уравнению (1.3) распределений гидродинамических величин в уравнения многомоментной гидродинамики [5, гл. 5] приводит к замкнутой нелинейной системе дифференциальных уравнений n-порядка для безразмерных коэффициентов ${{\hat {С}}_{i}}(t){\text{:}}$
(1.4)
$\frac{{\partial {{{\hat {С}}}_{i}}}}{{\partial t}} = {{F}_{i}}({{\hat {С}}_{1}},...,{{\hat {С}}_{n}}),\,\,\,\,i = 1,...,n.$Соотношения связи безразмерных коэффициентов ${{\hat {С}}_{i}}$ с коэффициентами ${{c}_{{klmn}}}$ из уравнения (1.3) представлены в работе [12]. Пусть ${{\hat {С}}_{i}}^{{(\alpha )}}(t)$ есть α-решение системы (1.4); тогда $\hat {\bar {С}}_{i}^{{(\alpha )}}$ есть стационарная составляющая $\alpha $-решения, а составляющая $\delta \hat {С}_{i}^{{r(\alpha )}}(t)$ появляется в результате потери устойчивости решения $\hat {\bar {С}}_{i}^{{(\alpha )}}.$ Нестационарное решение $\delta \hat {С}_{i}^{{r(\alpha )}}(t)$ является гидродинамическим отклонением от стационарного решения $\hat {\bar {С}}_{i}^{{(\alpha )}}$ [10]: ${{\hat {С}}_{i}}^{{(\alpha )}}(t)$ $ = \hat {\bar {С}}_{i}^{{(\alpha )}} + \delta \hat {С}_{i}^{{r(\alpha )}}(t),$ $i = 1,...,n.$
Сохранение трех низших членов разложения (1.3), линейных по ${{F}_{{xy}}},$ ${{F}_{{zy}}}$ и ${{F}_{{zx}}},$ дало классическое решение Стокса, справедливое в пределе $Re \ll 1$ [10]. Для увеличения Re помимо стоксовских членов в работе [10] сохранены следующие низшие члены разложения (1.3). Замкнутая нелинейная система из 20-ти дифференциальных уравнений для 20-ти коэффициентов ${{\hat {С}}_{i}},$ $i = 1,...,20,$ обозначена как St2. Решение $\hat {С}_{i}^{{(0)}}(t) = \hat {\bar {С}}_{i}^{{(0)}} + \delta \hat {С}_{i}^{{r(0)}}(t),$ $i = 1,...,20,$ системы St2 позволяет рассчитать распределения всех главных гидродинамических величин. Коэффициенты $\hat {C}_{1}^{{(0)}},$ $\hat {C}_{2}^{{(0)}},$ $\hat {C}_{3}^{{(0)}}$ и $\hat {C}_{4}^{{(0)}}$ ответственны за распределение плотности числа частиц, коэффициенты $\hat {C}_{5}^{{(0)}},$ $\hat {C}_{6}^{{(0)}},$ $\hat {C}_{7}^{{(0)}},$ $\hat {C}_{8}^{{(0)}},$ $\hat {C}_{9}^{{(0)}},$ $\hat {C}_{{18}}^{{(0)}}$ и $\hat {C}_{{19}}^{{(0)}}$ задают распределение давления и напряжений, коэффициенты $\hat {C}_{{10}}^{{(0)}},$ $\hat {C}_{{11}}^{{(0)}},$ $\hat {C}_{{12}}^{{(0)}},$ $\hat {C}_{{13}}^{{(0)}},$ $\hat {C}_{{15}}^{{(0)}},$ $\hat {C}_{{16}}^{{(0)}}$ и $\hat {C}_{{17}}^{{(0)}}$ ответственны за распределения тепловых потоков, коэффициенты $\hat {C}_{{14}}^{{(0)}}$ и $\hat {C}_{{20}}^{{(0)}}$ задают распределение скорости течения. В частности, выражение для плотности потока числа частиц принимает вид
(1.5)
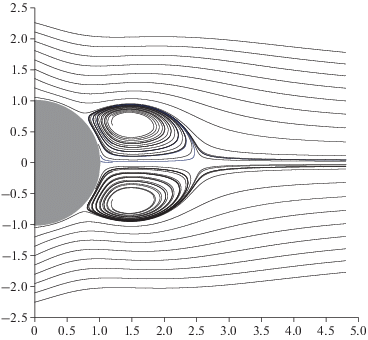
$\begin{gathered} n{{U}_{r}} = {{n}_{0}}{{U}_{0}}\left[ {\cos {\theta }\left( {1 - \frac{3}{2}\frac{a}{r} + \frac{1}{2}\frac{{{{a}^{3}}}}{{{{r}^{3}}}}} \right) + M{{a}^{2}}\hat {C}_{{14}}^{{(0)}} \times } \right. \\ \times \,\,\frac{1}{{15}}(3\cos \theta - 5{{\cos }^{3}}\theta )\frac{a}{r}{{\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right)}^{2}} + \\ \left. { + \,\,\operatorname{Re} \hat {C}_{{20}}^{{(0)}}\left( {3 - 30{{{\cos }}^{2}}{\theta } + 35co{{s}^{4}}{\theta }} \right)\frac{{{{a}^{2}}}}{{{{r}^{2}}}}{{{\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right)}}^{2}}} \right], \\ n{{U}_{{\theta }}} = {{n}_{0}}{{U}_{0}}\left[ {\sin {\theta }\left( { - 1 + \frac{3}{4}\frac{a}{r} + \frac{1}{4}\frac{{{{a}^{3}}}}{{{{r}^{3}}}}} \right) + M{{a}^{2}}\hat {C}_{{14}}^{{(0)}} \times } \right. \\ \times \,\,\frac{1}{{60}}\sin \theta \left( {1 - 5{{{\cos }}^{2}}\theta } \right)\frac{a}{r}\left( { - 1 - 2\frac{{{{a}^{2}}}}{{{{r}^{2}}}} + 3\frac{{{{a}^{4}}}}{{{{r}^{4}}}}} \right) + \\ \left. { + \,\,\operatorname{Re} \hat {C}_{{20}}^{{(0)}}\sin {\theta }\left( {12\cos {\theta } - 28co{{s}^{3}}{\theta }} \right)\frac{{{{a}^{4}}}}{{{{r}^{4}}}}\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right)} \right]. \\ \end{gathered} $В уравнении (1.5) ${{n}_{0}}$ – плотность невозмущенной среды, $\operatorname{Re} = {{m{{n}_{0}}{{U}_{0}}2a} \mathord{\left/ {\vphantom {{m{{n}_{0}}{{U}_{0}}2a} {\eta }}} \right. \kern-0em} {\eta }},$ $M{{a}^{2}} = {{mU_{0}^{2}} \mathord{\left/ {\vphantom {{mU_{0}^{2}} {k{{T}_{0}}}}} \right. \kern-0em} {k{{T}_{0}}}},$ η – коэффициент динамической вязкости. В случае $M{{a}^{2}} \ll 1$ пропорциональная $\hat {C}_{{20}}^{{(0)}}$ составляющая наряду со стоксовской составляющей вносит доминирующий вклад в распределение скорости. В соответствии со стационарным решением $\hat {\bar {С}}_{i}^{{(0)}},$ $i = 1,...,20,$ осесимметричная зона закручивания образуется в следе за сферой при $Re\sim 20$ [10]. Эта зона закручивания обладает формой осесимметричного тороидального кольца. По мере роста Re зона закручивания увеличивается в размерах, сохраняя свою форму (рис. 1).
Рис. 1.
Картина течения, представленная линиями тока: зона закручивания в следе за сферой; $\operatorname{Re} \hat {\bar {C}}_{{20}}^{{(0)}} = 0.488.$
Численное интегрирование системы St2 показало, что стационарное решение $\hat {\bar {C}}_{i}^{{(0)}},$ $i = 1,...,20,$ остается устойчивым вплоть до некоторого критического значения $Re_{0}^{*} = 129.1$ [10]. Это означает, что при $Re < Re_{0}^{*}$ малые отклонения $\delta \hat {C}_{i}^{{r(0)}}(t)$ от решения $\hat {\bar {C}}_{i}^{{(0)}}$ затухают. После достижения $Re_{0}^{*}$ стационарное решение $\hat {\bar {C}}_{i}^{{(0)}}$ теряет устойчивость. А именно, при $Re > Re_{0}^{*}$ затухание малых отклонений $\delta \hat {C}_{i}^{{r(0)}}(t)$ прекращается. Начиная с момента $t = 0$ малые отклонения $\delta \hat {C}_{i}^{{r(0)}}(t)$ от решения $\hat {\bar {C}}_{i}^{{(0)}}$ начинают экспоненциально нарастать. Гидродинамическое отклонение $\delta \hat {C}_{i}^{{r(0)}}(t)$ осесимметрично. Нарастание гидродинамического отклонения $\delta \hat {C}_{i}^{{r(0)}}(t)$ происходит вплоть до момента времени $t = {{t}_{ * }} > 0.$ В момент времени ${{t}_{ * }}$ решение $\delta \hat {C}_{i}^{{r(0)}}(t)$ обрывается. Причина обрыва решения $\hat {С}_{i}^{{(0)}}(t)$ = = $\hat {\bar {С}}_{i}^{{(0)}} + \delta \hat {C}_{i}^{{r(0)}}(t)$ проанализирована в [10].
Оказывается, что в окрестности точки обрыва существует решение ${{\hat {С}}_{i}}^{{*(0)}}(t*)$ = $\hat {\bar {С}}_{i}^{{(0)}} + \delta \hat {С}_{i}^{{*r(0)}}(t*),$ $i = 1,...,20,$ системы так называемых обратных уравнений многомоментной гидродинамики [5, гл. 7]. Замкнутая нелинейная система из 20-ти дифференциальных уравнений для 20-ти коэффициентов $\hat {С}_{i}^{*}(t*)$ обозначена как St*2 [10]. Система St*2 идентична системе St2, время t* отсчитывается в прогрессирующем направлении вдоль временнóй оси, направленной из будущего в прошлое. Соотношение связи времен на разных осях времени имеет вид $t* = t$ [5, гл. 7].
В соответствии с законом больших чисел появление в системе больших спонтанных флуктуаций является чрезвычайно редким событием. Закон больших чисел нарушается в окрестностях сингулярностей (бифуркаций, областей сосуществования нескольких решений и т.д.), и появление больших спонтанных флуктуаций в системе становится вполне вероятным [13]. В соответствии с [13] в момент времени $t = {{t}_{*}}$ большая спонтанная флуктуация вызывает переход системы из точки обрыва решения $\hat {C}_{i}^{{(0)}}(t = {{t}_{*}})$ к решению $\hat {C}_{i}^{{*(0)}}(t* = {{t}_{*}}).$ С момента $t* = {{t}_{*}}$ осесимметричное гидродинамическое отклонение $\delta \hat {C}_{i}^{{*r(0)}}(t*)$ решения $\hat {\bar {C}}_{i}^{{(0)}}$ начинает экспоненциально затухать в соответствии с системой уравнений St*2. К моменту времени $t* = 2{{t}_{*}}$ решение $\hat {C}_{i}^{{*(0)}}(t*)$ достигает окрестности стационарного решения $\hat {\bar {С}}_{i}^{{(0)}}.$ В момент времени $t* = 2{{t}_{*}}$ дальнейшая эволюция решения $\hat {C}_{i}^{{*(0)}}(t*)$ прекращается. То есть начиная с момента $t* = 2{{t}_{*}}$ система St*2 становится непригодной для моделирования дальнейшей эволюции физической системы. Стационарное решение $\hat {\bar {C}}_{i}^{{(0)}}$ системы St2 неустойчиво. Поэтому малые осесимметричные отклонения $\delta \hat {C}_{i}^{{r(0)}}(t)$ от решения $\hat {\bar {C}}_{i}^{{(0)}}$ начинают нарастать с момента времени $t = 2{{t}_{*}}.$ Процесс периодически повторяется. Решение $С_{i}^{{(0)}}(t)$ существует в диапазоне $0 < t < {{t}_{*}}.$ Решение $\hat {C}_{i}^{{*(0)}}(t*)$ существует в диапазоне ${{t}_{*}} < t* < 2{{t}_{*}}.$ Решения $\hat {C}_{i}^{{(0)}}(t)$ и $\hat {C}_{i}^{{*(0)}}(t*),$ $i = 1,...,20,$ обозначены в [12] как Sol0.
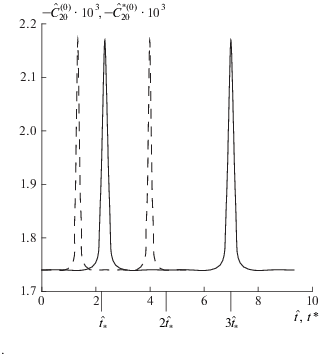
Поведение во времени гидродинамического отклонения ${\delta }\hat {C}_{i}^{{r(0)}}(t)$ и ${\delta }\hat {C}_{i}^{{*r(0)}}(t*),$ $i = 20,$ для Re = 180 представлено на рис. 2 сплошной кривой. Результатом такого поведения являются осесимметричные пульсации периферии зоны закручивания в следе за сферой (см. рис. 1). Тыльная сторона зоны закручивания устойчиво привязана к поверхности сферы. Пульсирующая периферия зоны закручивания не проявляет ни малейших признаков отрыва от ядра зоны закручивания.
2. ПОСЛЕДСТВИЯ РАСПАДА АНСАМБЛЯ ГИББСА В СИСТЕМЕ, ПОТЕРЯВШЕЙ УСТОЙЧИВОСТЬ
Функции $\hat {C}_{{20}}^{{(0)}}(t)$ и $\hat {C}_{{20}}^{{*(0)}}(t*),$ представленные на рис. 2 сплошной кривой, соответствуют начальным отклонениям $\delta \hat {C}_{i}^{{r(0)}}(t = 0)$ ∼ ${{10}^{{ - 9}}} - {{10}^{{ - 10}}},$ $i = 1,...,20.$ Штриховой кривой на рис. 2 представлены функции $\hat {C}_{{20}}^{{(0)}}(t)$ и $\hat {C}_{{20}}^{{*(0)}}(t*),$ рассчитанные при $\delta \hat {C}_{i}^{{r(0)}}(t = 0)$ ∼ ${{10}^{{ - 6}}} - {{10}^{{ - 7}}},$ $i = 1,...,20.$ Таким образом, нелинейные системы St2 и St*2 “разводят” первоначально близкие решения. Такая чувствительность к начальным условиям называется эффектом бабочки Лоренца [14].
Уравнения многомоментной гидродинамики, как и уравнения классической гидродинамики, описывают, вообще говоря, пространственно-временную эволюцию не какой-либо отдельной системы, а целого ансамбля систем (ансамбля Гиббса) [15]. Каждая отдельная система обладает всеми возможными значениями микроскопических параметров, совместимых с изначально заданными значениями макроскопических параметров. При этом макроскопические параметры системы задаются не точно, а в определенных пределах, соответствующих порядку возможных флуктуаций. Таким образом, каждый статистический коэффициент $\hat {C}_{i}^{{(0)}}(t),$ $i = 1,...,20,$ представляется в виде линейной комбинации огромного числа L (в пределе бесконечно большого) динамических коэффициентов $\hat {C}_{{i(j)}}^{{D(0)}}(t),$ $j = 1,...,L,$ $L \gg 1.$ Каждый динамический коэффициент $\hat {C}_{{i(j)}}^{{D(0)}}(t)$ рассчитывается в рамках классической механики. Флуктуация $\delta \hat {C}_{i}^{{(0)}}(t)$ коэффициента $\hat {C}_{i}^{{(0)}}(t)$ определяется в любой момент времени разностью динамического и статистического коэффициентов,
или, что эквивалентно, разностью двух произвольных динамических коэффициентов,
Рассмотрим диапазон параметров системы ($Re < Re_{0}^{*}$), в котором уравнение (1.4) для статистических коэффициентов $\hat {C}_{i}^{{}}(t)$ имеет устойчивое решение: $\hat {\bar {C}}_{i}^{{(0)}},$ $i = 1,...,20,$ В этом диапазоне подавляющее большинство динамических траекторий $\hat {C}_{{i(j)}}^{{D(0)}}(t),$ $j = 1,...,L,$ $L \gg 1,$ находившихся в момент $t = 0$ в непосредственной близости от решения $\hat {\bar {C}}_{i}^{{(0)}}$ ($\delta \hat {C}_{i}^{{(0)}}(t = 0)$ = $\hat {C}_{{i(j)}}^{{D(0)}}(t = 0) - \hat {\bar {C}}_{i}^{{(0)}} \ll 1$), будет и далее сколь угодно долго находиться вблизи $\hat {\bar {C}}_{i}^{{(0)}}$ ($\delta \hat {C}_{i}^{{(0)}}(t)$ ≈ $\delta \hat {C}_{i}^{{(0)}}(t = 0)$). Статистическое решение $\hat {\bar {C}}_{i}^{{(0)}}$ описывает подавляющее большинство динамических траекторий $\hat {C}_{{i(j)}}^{{D(0)}}(t),$ $j = 1,...,L,$ с точностью $\delta \hat {C}_{i}^{{(0)}}(t = 0) \ll 1.$
Совершенно иная ситуация имеет место в неустойчивой области ($Re > Re_{0}^{*}$). В соответствии с рис. 2 изначально близкие траектории расходятся (сплошная и штриховая кривые). Отсюда непосредственно следует, что каждый динамический j-коэффициент $\hat {C}_{{i(j)}}^{{D(0)}}(t)$ ведет себя сугубо индивидуально. Не существует единого для всего ансамбля коэффициента $\hat {C}_{i}^{{(0)}}(t),$ $i = 1,...,20,$ который с флуктуационной точностью $\delta \hat {C}_{i}^{{(0)}}(t = 0) \ll 1$ описал бы любой из совокупности динамических коэффициентов $\hat {C}_{{i(j)}}^{{D(0)}}(t),$ $j = 1,...,L,$ $L \gg 1.$ Ансамбль Гиббса распадается.
Распад ансамбля Гиббса в области неустойчивости означает следующее. Во-первых, любой статистический коэффициент $\hat {C}_{i}^{{(0)}}(t),$ являющийся средним по L динамическим коэффициентам, ведет себя сугубо индивидуально, подобно j-динамическому коэффициенту $\hat {C}_{{i(j)}}^{{D(0)}}(t).$ Разность двух произвольных динамических коэффициентов $\hat {C}_{{i(j)}}^{{D(0)}}(t)$ – $\hat {C}_{{i(k)}}^{{D(0)}}(t)$ дает оценку величины флуктуации коэффициента $\hat {\bar {C}}_{i}^{{(0)}},$ $i = 1,...,20.$ Следовательно, гидродинамическое отклонение $\delta \hat {C}_{i}^{{r(0)}}(t)$ = $\hat {C}_{i}^{{(0)}}(t) - \hat {\bar {C}}_{i}^{{(0)}}$ есть не что иное, как флуктуация стационарного коэффициента $\hat {\bar {C}}_{i}^{{(0)}}.$ Эти флуктуации взаимосвязаны как во времени, так и в пространстве. Вот почему гидродинамические отклонения $\delta \hat {С}_{i}^{{r(0)}}(t)$ названы регулярными флуктуациями стационарного решения $\hat {\bar {С}}_{i}^{{(0)}},$ $\hat {С}_{i}^{{(0)}}(t)$ = $\hat {\bar {С}}_{i}^{{(0)}} + \delta \hat {С}_{i}^{{r(0)}}(t),$ $i = 1,...,20$ [10].
Во-вторых, классическое кинетическое уравнение, а также уравнения для парных функций распределения, используемые для описания ансамбля Гиббса в целом, строго говоря, не справедливы в области, где эти уравнения теряют устойчивость. Закон Ньютона для тензора вязких напряжений ${{p}_{{ij}}}$ и закон Фурье для вектора теплового потока q выведены непосредственно из уравнения Больцмана, справедливого для ансамбля систем в целом [16]. Выражения для диссипативных моментов, тензора вязких напряжений $p_{{ij}}^{{v}}$ и вектора теплового потока ${{q}^{{G{v}}}} - \left( {1{\text{/}}3} \right){{q}^{{v}}},$ в терминах главных гидродинамических величин получены непосредственно из уравнений для парных функций распределения. Выражения для $p_{{ij}}^{{v}}$ и ${{q}^{{G{v}}}} - \left( {1{\text{/}}3} \right){{q}^{{v}}}$ также справедливы для ансамбля систем в целом. Таким образом, ни уравнения многомоментной гидродинамики, ни уравнения Навье–Стокса, вообще говоря, не пригодны для описания пространственно-временного поведения системы, потерявшей устойчивость. Основное свойство парных функций (1.1) также справедливо для ансамбля систем в целом. После потери устойчивости коэффициенты $\hat {C}_{i}^{{(0)}}$ приобретают зависимость от времени. В результате парная функция распределения ${{f}_{p}}(t,x,G,{v})$ утрачивает постоянство на прямой линии, параллельной вектору G. Невыполнение основного свойства (1.1) не позволяет провести разбиение уравнений сохранения импульса и энергии на отдельные составляющие [5, гл. 5].
Для решения задачи моделирования флуктуаций, строго говоря, необходимо перейти от статистического к динамическому уровню описания и использовать уравнения классической механики, описывающие динамику каждой частицы газа. Однако численное интегрирование уравнений классической механики для системы, состоящей из огромного числа частиц (в пределе бесконечно большого), является трудноосуществимой на практике задачей. Более того, этот путь представляется крайне нерациональным. Поэтому решение задачи моделирования флуктуаций следует искать на статистическом уровне, т.е. на основе уравнений многомоментной гидродинамики [5, гл. 5].
В задаче с не зависящими от времени граничными условиями будем строить регулярную составляющую парной функции распределения ${{f}_{p}}(t,x,G,{v})$ в виде ряда (1.3) как в устойчивом поле $\operatorname{Re} < \operatorname{Re} _{0}^{*},$ так и при потере устойчивости ($\operatorname{Re} \geqslant \operatorname{Re} _{0}^{*}$). Ряд (1.3) задает пространственное распределение функции ${{f}_{p}}(t,x,G,{v}),$ зависимость от времени определяется коэффициентами ${{\hat {C}}_{i}}(t).$ Как в устойчивом ($\operatorname{Re} < \operatorname{Re} _{0}^{*}$), так и в неустойчивом поле ($\operatorname{Re} \geqslant \operatorname{Re} _{0}^{*}$) выразим регулярную составляющую неглавных гидродинамических величин $p_{{ij}}^{{v}}$ и ${{q}^{{G{v}}}} - \left( {1{\text{/}}3} \right){{q}^{{v}}}$ в терминах регулярной составляющей главных гидродинамических величин ([5, гл. 5]). Подстановка рассчитанных гидродинамических величин в уравнения многомоментной гидродинамики приводит к замкнутой нелинейной системе дифференциальных уравнений (1.4). После достижения критического значения числа Рейнольдса $\operatorname{Re} _{0}^{*}$ стационарное решение $\hat {\bar {C}}_{i}^{{(0)}},$ $i = 1,...,20,$ системы St2 теряет свою устойчивость. Разделение уравнений сохранения на отдельные составляющие становится некорректным. Потерявшее устойчивость решение уже не может удовлетворить законам сохранения [10]. Причиной этого стала зависимость от времени, которую коэффициенты $\hat {C}_{i}^{{(0)}}$ приобретают после потери устойчивости. Таким образом, учет лишь регулярной составляющей $\delta \hat {C}_{i}^{{r(0)}}(t)$ нестационарного решения $\hat {C}_{i}^{{(0)}}(t)$ не обеспечивает выполнение законов сохранения.
Решение этой проблемы может быть найдено за счет учета неупорядоченных возмущений, существующих в реальной физической системе. Неупорядоченное возмущение появляется в среде за счет внешнего воздействия, оно является случайным событием в каждой точке пространства x. В работе [17] при моделировании индивидуальной системы каждая гидродинамическая величина в уравнениях сохранения дополнялась хаотической флуктуационной компонентой. Следуя представлениям из [17], проведем учет неупорядоченных возмущений. Будем искать флуктуацию $\delta \hat {C}_{{20,i}}^{{(0)}}(t,x)$ статистического коэффициента $\hat {\bar {C}}_{{20}}^{{(0)}},$ который доминирует в распределении скорости течения (1.5), в виде линейной комбинации независимых составляющих:
(2.1)
$\delta \hat {C}_{{20,i}}^{{(0)}}(t,x) = \delta \hat {C}_{{20}}^{{r(0)}}(t) + \delta \hat {C}_{{20,i}}^{{d(0)}}(t,x).$В уравнении (2.1) $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ – регулярная флуктуация стационарного решения $\hat {\bar {C}}_{{20}}^{{(0)}}$ системы уравнений St2, $\delta \hat {C}_{{20,i}}^{{d(0)}}(t,x)$ – неупорядоченное возмущение коэффициента $\hat {\bar {C}}_{{20}}^{{(0)}},$ отвечающее i-компоненте скорости течения, $i = r,\theta .$ Наряду с $\delta \hat {C}_{{20,i}}^{{d(0)}}(t,x)$ зададим модуль неупорядоченного возмущения $\delta \hat {C}_{{20}}^{{d(0)}}(t,x),$ который отвечает модулю скорости течения. Флуктуация $\delta \hat {C}_{{20,i}}^{{(0)}}(t,x)$ стационарного решения $\hat {\bar {C}}_{{20}}^{{(0)}}$ определяет коэффициент $\hat {C}_{{20,i}}^{{(0)}}(t,x){\text{:}}$
(2.2)
$\hat {C}_{{20,i}}^{{(0)}}(t,x) = \hat {\bar {C}}_{{20}}^{{(0)}} + \delta \hat {C}_{{20.i}}^{{(0)}}(t,x).$Подставим выражение (2.2) для коэффициента $\hat {C}_{{20,i}}^{{(0)}}(t,x)$ в доминирующий член распределения плотности потока частиц $nU$ (уравнение (1.5)). Полученное аналитическое распределение учитывает регулярные флуктуации и неупорядоченные возмущения:
(2.3)
$\begin{gathered} n{{U}_{r}} = {{n}_{0}}{{U}_{0}}\cos {\theta }\left( {1 - \frac{3}{2}\frac{a}{r} + \frac{1}{2}\frac{{{{a}^{3}}}}{{{{r}^{3}}}}} \right) + \\ + \,\,{{n}_{0}}M{{a}^{2}}{{U}_{r}}(\hat {C}_{{14}}^{{(0)}}) + {{n}_{0}}{{U}_{0}}\operatorname{Re} \hat {\bar {C}}_{{20}}^{{(0)}} \times \\ \times \,\,\left( {3 - 30{{{\cos }}^{2}}{\theta } + 35co{{s}^{4}}{\theta }} \right)\frac{{{{a}^{2}}}}{{{{r}^{2}}}} \times \\ \times \,\,{{\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right)}^{2}} + {{n}_{0}}\left( {\delta U_{r}^{{(r)}} + \delta U_{r}^{{(d)}}} \right), \\ n{{U}_{{\theta }}} = {{n}_{0}}{{U}_{0}}\sin {\theta }\left( { - 1 + \frac{3}{4}\frac{a}{r} + \frac{1}{4}\frac{{{{a}^{3}}}}{{{{r}^{3}}}}} \right) + \\ + \,\,{{n}_{0}}M{{a}^{2}}{{U}_{{\theta }}}\left( {\hat {C}_{{14}}^{{(0)}}} \right) + {{n}_{0}}{{U}_{0}}\operatorname{Re} \hat {\bar {C}}_{{20}}^{{(0)}}\sin {\theta } \times \\ \times \,\,\left( {12\cos {\theta } - 28co{{s}^{3}}{\theta }} \right)\frac{{{{a}^{4}}}}{{{{r}^{4}}}}\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right) + \\ + \,\,{{n}_{0}}\left( {\delta U_{{\theta }}^{{(r)}} + \delta U_{{\theta }}^{{(d)}}} \right). \\ \end{gathered} $В уравнении (2.3) $U(\hat {C}_{{14}}^{{(0)}})$ – составляющая скорости течения, пропорциональная коэффициенту $\hat {C}_{{14}}^{{(0)}},$ $\delta U_{{}}^{{(r)}}$ – регулярная флуктуация составляющей скорости течения, пропорциональная стационарному решению $\hat {\bar {C}}_{{20}}^{{(0)}}{\text{:}}$
(2.4)
$\begin{gathered} \delta U_{r}^{{(r)}} = {{U}_{0}}\delta \hat {U}_{r}^{{(r)}} = {{U}_{0}}\delta {{{\hat {U}}}^{{r(0)}}}\left( {3 - 30{{{\cos }}^{2}}{\theta }\,{\text{ + }}} \right. \\ \left. { + \,\,35co{{s}^{4}}{\theta }} \right)\frac{{{{a}^{2}}}}{{{{r}^{2}}}}{{\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right)}^{2}},\,\,\,\,\delta U_{{\theta }}^{{(r)}} = {{U}_{0}}\delta \hat {U}_{{\theta }}^{{(r)}} = \\ = {{U}_{0}}\delta {{{\hat {U}}}^{{r(0)}}}\sin {\theta }\left( {12\cos {\theta } - 28co{{s}^{3}}{\theta }} \right)\frac{{{{a}^{4}}}}{{{{r}^{4}}}}\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right), \\ \end{gathered} $где $\delta {{\hat {U}}^{{r(0)}}}$ = $\operatorname{Re} \delta \hat {C}_{{20}}^{{r(0)}};$ $\delta {{U}^{{(d)}}}$ – неупорядоченное возмущение составляющей скорости течения, пропорциональное стационарному решению $\hat {\bar {C}}_{{20}}^{{(0)}}{\text{:}}$
(2.5)
$\begin{gathered} \delta U_{r}^{{(d)}} = {{U}_{0}}\delta \hat {U}_{r}^{{(d)}} = {{U}_{0}}\delta \hat {U}_{r}^{{d(0)}}\left( {3 - 30{{{\cos }}^{2}}{\theta } + } \right. \\ \left. { + \,\,35co{{s}^{4}}{\theta }} \right)\frac{{{{a}^{2}}}}{{{{r}^{2}}}}{{\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right)}^{2}},\,\,\,\,\delta U_{{\theta }}^{{(d)}} = {{U}_{0}}\delta \hat {U}_{{\theta }}^{{(d)}} = \\ = {{U}_{0}}\delta \hat {U}_{{\theta }}^{{d(0)}}\sin {\theta }\left( {12\cos {\theta } - 28co{{s}^{3}}{\theta }} \right)\frac{{{{a}^{4}}}}{{{{r}^{4}}}}\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right). \\ \end{gathered} $Здесь $\delta \hat {U}_{i}^{{d(0)}}$ = $\operatorname{Re} \delta \hat {C}_{{20,i}}^{{d(0)}},$ величина $\delta {{\hat {U}}^{{d(0)}}}$ = $\operatorname{Re} \delta \hat {C}_{{20}}^{{d(0)}}$ есть модуль неупорядоченного возмущения скорости течения. Коэффициенты $\hat {C}_{5}^{{(0)}},$ $\hat {C}_{6}^{{(0)}},$ $\hat {C}_{7}^{{(0)}},$ $\hat {C}_{8}^{{(0)}},$ $\hat {C}_{9}^{{(0)}},$ $\hat {C}_{{18}}^{{(0)}}$ и $\hat {C}_{{19}}^{{(0)}}$ ответственны за распределение давления ${{p}^{G}}$ и тензора напряжений $p_{{kl}}^{G},$ создаваемых в результате движения центров масс пар частиц [10]. По аналогии с уравнением (2.1) будем искать флуктуацию статистического коэффициента $\hat {\bar {C}}_{i}^{{(0)}},$ $i = 5,\,\,...,\,\,9,\,\,18,\,\,19,$ в виде
(2.6)
$\begin{gathered} \delta \hat {C}_{i}^{{(0)}}(t,x) = \delta \hat {C}_{i}^{{r(0)}}(t) + \delta \hat {C}_{i}^{{d(0)}}(t,x), \\ \hat {C}_{i}^{{(0)}}(t,x) = \hat {\bar {C}}_{i}^{{(0)}} + \delta \hat {C}_{i}^{{(0)}}(t,x),\,\,\,\,i = 5,\,\,6,\,\,7,\,\,19, \\ \delta \hat {C}_{{i,kl}}^{{(0)}}(t,x) = \delta \hat {C}_{i}^{{r(0)}}(t) + \delta \hat {C}_{{i,kl}}^{{d(0)}}(t,x), \\ \hat {C}_{{i,kl}}^{{(0)}}(t,x) = \hat {\bar {C}}_{i}^{{(0)}} + \delta \hat {C}_{{i,kl}}^{{(0)}}(t,x),\,\,\,\,i = 5,\,\,...,\,\,9,\,\,18,\,\,19. \\ \end{gathered} $В уравнении (2.6) $\delta \hat {C}_{i}^{{r(0)}}(t)$ есть регулярная флуктуация коэффициента $\hat {\bar {C}}_{i}^{{(0)}},$ $\delta \hat {C}_{i}^{{d(0)}}(t,x)$ и $\delta \hat {C}_{{i,kl}}^{{d(0)}}(t,x)$ являются неупорядоченными возмущениями коэффициента $\hat {\bar {C}}_{i}^{{(0)}}.$ Коэффициенты $\hat {C}_{i}^{{(0)}}(t,x)$ ответственны за давление ${{p}^{G}},$ а коэффициенты $\hat {C}_{{i,kl}}^{{(0)}}(t,x)$ – за тензор напряжений $p_{{kl}}^{G}{\text{:}}$
(2.7)
$\begin{gathered} {{p}^{G}} = {{n}_{0}}k{{T}_{0}}M{{a}^{2}}\sum\limits_i {\hat {\bar {C}}_{i}^{{(0)}}{{f}^{{(i)}}}(r,\theta )} + {{n}_{0}}k{{T}_{0}} \times \\ \times \,\,\left( {\delta {{{\hat {p}}}^{{G(r)}}} + \delta {{{\hat {p}}}^{{G(d)}}}} \right),\,\,i = 5,\,\,6,\,\,7,\,\,19, \\ p_{{kl}}^{G} = {{n}_{0}}k{{T}_{0}}M{{a}^{2}}\sum\limits_i {\hat {\bar {C}}_{{i,kl}}^{{(0)}}f_{{kl}}^{{(i)}}(r,\theta )} + {{n}_{0}}k{{T}_{0}} \times \\ \times \,\,\left( {\delta \hat {p}_{{kl}}^{{G(r)}} + \delta \hat {p}_{{kl}}^{{G(d)}}} \right),\,\,\,\,i = 5,\,\,...,\,\,9,\,\,18,\,\,19. \\ \end{gathered} $В уравнении (2.7) $\delta {{\hat {p}}^{{G(r)}}}$ и $\delta {{\hat {p}}^{{G(d)}}}$ – соответственно регулярная флуктуация и неупорядоченное возмущение давления ${{p}^{G}}{\text{:}}$
(2.8)
$\begin{gathered} \delta {{{\hat {p}}}^{{G(r)}}} = M{{a}^{2}}\sum\limits_i {\delta \hat {C}_{i}^{{r(0)}}{{f}^{{(i)}}}(r,\theta )} ,\, \\ \delta {{{\hat {p}}}^{{G(d)}}} = M{{a}^{2}}\sum\limits_i {\delta \hat {C}_{i}^{{d(0)}}{{f}^{{(i)}}}(r,\theta )} ,\,\,\,\,i = 5,\,\,6,\,\,7,\,\,19; \\ \end{gathered} $$\delta \hat {p}_{{kl}}^{{G(r)}}$ и $\delta \hat {p}_{{kl}}^{{G(d)}}$ – соответственно регулярные флуктуации и неупорядоченные возмущения тензора напряжений $p_{{kl}}^{G}{\text{:}}$
(2.9)
$\begin{gathered} \delta \hat {p}_{{kl}}^{{G(r)}} = M{{a}^{2}}\sum\limits_i {\delta \hat {C}_{i}^{{r(0)}}f_{{kl}}^{{(i)}}(r,\theta )} ,\, \\ \delta \hat {p}_{{kl}}^{{G(d)}} = M{{a}^{2}}\sum\limits_i {\delta \hat {C}_{{i,kl}}^{{d(0)}}f_{{kl}}^{{(i)}}(r,\theta )} ,\,\,i = 5,\,...,\,9,\,\,18,\,\,19. \\ \end{gathered} $Пространственную структуру безразмерных функций $f_{{}}^{{(i)}}(r,\theta )$ и $f_{{kl}}^{{(i)}}(r,\theta )$ определяют произведения ${{(a{\text{/}}r)}^{j}}{{\cos }^{m}}\theta {{\sin }^{n}}\theta $ с нечетными j и четными $m + n$ или четными j и нечетными $m + n$ (см. уравнения (4.6) и (4.7) в [12]).
Гидродинамические величины U, $p_{{}}^{G}$ и $p_{{kl}}^{G}$ являются составляющими уравнения сохранения импульса [5, гл. 5]:
(2.10)
$\begin{gathered} \frac{{\partial n{{U}_{k}}}}{{\partial t}} + \frac{\partial }{{\partial {{x}_{l}}}}\left( {n{{U}_{k}}{{U}_{l}} + \frac{{{{p}^{G}}{{\delta }_{{kl}}} + p_{{kl}}^{G}}}{{2m}} + } \right. \\ \left. { + \,\,\frac{{{{p}^{{v}}}{{\delta }_{{kl}}} + p_{{kl}}^{{v}}}}{{2m}}} \right) = 0. \\ \end{gathered} $В уравнении (2.10) ${{p}^{{v}}}$ и $p_{{kl}}^{{v}}$ – соответственно давление и тензор напряжений, создаваемых в результате относительного движения частиц в паре. Следуя представлениям [17], учтем неупорядоченные возмущения давления ${{p}^{{v}}}$ в порядке величины ${{n}_{0}}k{{T}_{0}}M{{a}^{2}}$ (см. уравнение (4.5) из [12]):
(2.11)
$\begin{gathered} {{p}^{{v}}} = - 40{{n}_{0}}k{{T}_{0}}M{{a}^{2}}\hat {\bar {C}}_{{20}}^{{(0)}}\left( {3{{{\cos }}^{2}}\theta - 1} \right)\frac{{{{a}^{3}}}}{{{{r}^{3}}}} + \\ + \,\,{{n}_{0}}k{{T}_{0}}\left( {\delta {{{\hat {p}}}^{{{v}(r)}}} + \delta {{{\hat {p}}}^{{{v}(d)}}}} \right). \\ \end{gathered} $В уравнении (2.11) $\delta {{\hat {p}}^{{{v}(r)}}}$ и $\delta {{\hat {p}}^{{{v}(d)}}}$ – соответственно регулярная флуктуация и неупорядоченное возмущение давления ${{p}^{{v}}}.$ Выполнение уравнения сохранения импульса позволило выразить регулярные составляющие давления ${{p}^{{v}}}$ в терминах коэффициентов $\hat {\bar {C}}_{{20}}^{{(0)}}$ и $\hat {C}_{{20}}^{{r(0)}}(t).$ Однако разбиение уравнений сохранения импульса и энергии на отдельные составляющие становится некорректным после распада ансамбля Гиббса. Поэтому при построении неупорядоченного возмущения $\delta {{p}^{{{v}(d)}}}$ используются безразмерные функции ${{f}^{{(i)}}}(r,\theta )$ (уравнение (2.8)), которые определяют пространственную структуру давления ${{p}^{{v}}}$ (см. уравнение (П.2) в [10]):
(2.12)
$\begin{gathered} \delta {{{\hat {p}}}^{{{v}(r)}}} = - 40M{{a}^{2}}\delta \hat {C}_{{20}}^{{r(0)}}\left( {3{{{\cos }}^{2}}\theta - 1} \right)\frac{{{{a}^{3}}}}{{{{r}^{3}}}}, \\ \delta {{{\hat {p}}}^{{{v}(d)}}} = M{{a}^{2}}\sum\limits_i {\delta \hat {C}_{i}^{{d(0)}}{{f}^{{(i)}}}(r,\theta )} ,\,\,\,\,i = 23,\,\,...,\,\,26. \\ \end{gathered} $Неупорядоченное возмущение $\delta \hat {C}_{i}^{{d(0)}},$ $i = 23,\,\,...,\,\,26,$ интерпретирующее давление ${{p}^{{v}}}$ (уравнения (2.11) и (2.12)), вообще говоря, не связано с неупорядоченным возмущением $\delta \hat {C}_{{20}}^{{d(0)}}(t,x)$ статистического коэффициента $\hat {\bar {C}}_{{20}}^{{(0)}},$ интерпретирующего скорость течения U (уравнение (2.1)).
Решение уравнений для парных функций распределения дает выражение для тензора напряжений $p_{{kl}}^{{v}}$ ([5, гл. 5]),
(2.13)
$\begin{gathered} p_{{kl}}^{{v}} = - \eta \left( {\frac{{\partial {{U}_{k}}}}{{\partial {{x}_{l}}}} + \frac{{\partial {{U}_{l}}}}{{\partial {{x}_{k}}}} - \frac{2}{3}{{\delta }_{{kl}}}\frac{{\partial {{U}_{n}}}}{{\partial {{x}_{n}}}}} \right) - \\ - \,\,\frac{{2{\eta }}}{{3{{p}^{{v}}}}}\left( {\frac{{\partial q_{k}^{{v}}}}{{\partial {{x}_{l}}}} + \frac{{\partial q_{l}^{{v}}}}{{\partial {{x}_{k}}}} - \frac{2}{3}{{\delta }_{{kl}}}\frac{{\partial q_{n}^{{v}}}}{{\partial {{x}_{n}}}}} \right). \\ \end{gathered} $В уравнении (2.13) ${{q}^{{v}}}$ – тепловой поток, создаваемый в результате относительного движения частиц в паре. Запишем (2.13) в сферических координатах $r,\theta .$ Подставим распределение скорости течения U из уравнения (1.2) в первый член уравнения (2.13). Составляющая скорости течения U, пропорциональная ${{\hat {C}}_{{20}}},$ ответственна за порядок ${{n}_{0}}k{{T}_{0}}M{{a}^{2}}$ в уравнении (2.13) для $p_{{kl}}^{{v}}.$ Второй член в правой части (2.13) не вносит вклада в рассматриваемый порядок. Следуя представлениям из работы [17], учтем неупорядоченные возмущения тензора напряжений $p_{{kl}}^{{v}}$ в порядке величины ${{n}_{0}}k{{T}_{0}}M{{a}^{2}}{\text{:}}$
(2.14)
$p_{{kl}}^{{v}} = {{n}_{0}}k{{T}_{0}}M{{a}^{2}}\hat {\bar {C}}_{{20}}^{{(0)}}A_{{kl}}^{{v}} + {{n}_{0}}k{{T}_{0}}\left( {\delta \hat {p}_{{kl}}^{{{v}(r)}} + \delta \hat {p}_{{kl}}^{{{v}(d)}}} \right).$В уравнении (2.14) $\delta \hat {p}_{{kl}}^{{{v}(r)}}$ и $\delta \hat {p}_{{kl}}^{{{v}(d)}}$ – соответственно регулярная флуктуация и неупорядоченное возмущение тензора напряжений, пространственная структура безразмерных функций $A_{{kl}}^{{v}}$ определена в [10].
Однако представление диссипативных моментов в терминах главных гидродинамических величин становится некорректным после распада ансамбля Гиббса. В частности, уравнение (2.13) становится непригодным для интерпретации неупорядоченных возмущений. Будем строить неупорядоченные возмущения $\delta p_{{kl}}^{{{v}(d)}}$ тензора напряжений $p_{{kl}}^{{v}}$ (уравнение (2.14)) в терминах безразмерных функций $f_{{kl}}^{{(i)}}(r,\theta ),$ $i = 5,\,\,...,\,\,9,\,\,18,\,\,19,$ определяющих пространственную структуру тензора напряжений $p_{{kl}}^{G}$ (см. уравнение (4.7) в [12]). В этом случае функции $\delta \hat {p}_{{kl}}^{{{v}(r)}}$ и $\delta \hat {p}_{{kl}}^{{{v}(d)}}$ принимают вид
(2.15)
$\begin{gathered} \delta \hat {p}_{{kl}}^{{{v}(r)}} = M{{a}^{2}}\delta \hat {C}_{{20}}^{{r(0)}}A_{{kl}}^{{v}}, \\ \delta \hat {p}_{{kl}}^{{{v}(d)}} = M{{a}^{2}}\sum\limits_i {\delta \hat {C}_{{i,kl}}^{{d(0)}}f_{{kl}}^{{(i)}}(r,\theta )} ,\,\,\,\,i = 27,\,\,...,\,\,33. \\ \end{gathered} $Неупорядоченные возмущения $\delta \hat {C}_{{i,kl}}^{{d(0)}},$ $i = 27,...,33,$ являющиеся составляющими тензора напряжений $p_{{kl}}^{{v}}$ (уравнение (2.14)), вообще говоря, не связаны с неупорядоченным возмущением $\delta \hat {C}_{{20}}^{{d(0)}}(t,x)$ статистического коэффициента $\hat {\bar {C}}_{{20}}^{{(0)}},$ интерпретирующего скорость течения U (уравнение (2.1)).
Подставим выражение (2.3) для плотности потока частиц $nU,$ выражения (2.8) и (2.11) для давлений ${{p}^{G}}$ и ${{p}^{{v}}}$ и выражения (2.9) и (2.14) для тензоров напряжений $p_{{kl}}^{G}$ и $p_{{kl}}^{{v}}$ в уравнение сохранения импульса (2.10). Следуя общей идеологии решения уравнений многомоментной гидродинамики, приравняем к нулю выражения при каждом произведении ${{(a{\text{/}}r)}^{j}}{{\cos }^{m}}\theta {{\sin }^{n}}\theta $ с четными j и четными $m + n$ отдельно [10]. В результате получаем
(2.16)
$\begin{gathered} \frac{{\partial \delta C_{{20}}^{{r(0)}}(t)}}{{\partial t}} + \frac{{\partial \delta C_{{20,i}}^{{d(0)}}(t,x)}}{{\partial t}} + \\ + \,\,\frac{1}{{{{n}_{0}}ma}}F_{{20}}^{{(j,m + n)}}(t,x) = 0; \\ \end{gathered} $здесь
(2.17)
$\begin{gathered} \delta C_{{20}}^{{r(0)}}(t) = {{U}_{0}}\operatorname{Re} \delta \hat {C}_{{20}}^{{r(0)}}(t), \\ \delta C_{{20,i}}^{{d(0)}}(t,x) = {{U}_{0}}\operatorname{Re} \delta \hat {C}_{{20,i}}^{{d(0)}}(t,x). \\ \end{gathered} $В уравнении (2.17) функция $F_{{20}}^{{(j,m + n)}}(t,x)$ – линейная комбинация неупорядоченных возмущений $\delta C_{i}^{{d(0)}},$ $\delta C_{{i,kl}}^{{d(0)}}{\text{:}}$
(2.18)
$\begin{gathered} \delta C_{i}^{{d(0)}}(t,x) = {{n}_{0}}k{{T}_{0}}M{{a}^{2}}\delta \hat {C}_{i}^{{d(0)}}(t,x), \\ i = 5,\,\,6,\,\,7,\,\,19,\,\,23,\,\,...,\,\,26, \\ \delta C_{{i,kl}}^{{d(0)}}(t,x) = {{n}_{0}}k{{T}_{0}}M{{a}^{2}}\delta \hat {C}_{{i,kl}}^{{d(0)}}(t,x), \\ i = 5,\,\,...,\,\,9,\,\,18,\,\,19,\,\,27,\,\,...,\,\,33. \\ \end{gathered} $Функция $F_{{20}}^{{(j,m + n)}}(t,x)$ не содержит пространственных производных коэффициентов из (2.18).
Уравнения многомоментной гидродинамики (1.4) диктуют характерный временнóй масштаб изменения гидродинамических величин τh = $ = {{\operatorname{Re} a} \mathord{\left/ {\vphantom {{\operatorname{Re} a} {2{{U}_{0}}}}} \right. \kern-0em} {2{{U}_{0}}}},$ т.е. временнóй интервал ${{\tau }_{h}}$ является характерным масштабом изменения регулярной флуктуации $\delta C_{{20}}^{{r(0)}}$ [10]. Крупномасштабные неупорядоченные возмущения скорости течения ($\delta C_{{20,i}}^{{d(0)}}$ ∼ ${{{{U}_{0}}} \mathord{\left/ {\vphantom {{{{U}_{0}}} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}$) также обладают характерным масштабом изменения ${{\tau }_{h}}.$ Мелкомасштабные неупорядоченные возмущения скорости течения ($\delta C_{{20,i}}^{{d(0)}} \ll {{{{U}_{0}}} \mathord{\left/ {\vphantom {{{{U}_{0}}} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}$) изменяются на масштабе ${{\tau }_{d}} \ll {{\tau }_{h}}$. Мелкомасштабные неупорядоченные возмущения вносят пренебрежимо малый вклад в распределения гидродинамических величин, однако, вообще говоря, их производные по времени имеют основной порядок величины. Таким образом, учет неупорядоченных возмущений (крупномасштабных и мелкомасштабных) позволяет, в принципе, обеспечить выполнение закона сохранения импульса (2.16).
ЗАКЛЮЧЕНИЕ
Эксперимент регистрирует три устойчивых состояния среды при обтекании покоящейся твердой сферы. Основное устойчивое стационарное течение $U_{0}^{{exp}}(x)$ обладает осесимметричной торообразной зоной закручивания в ближнем следе за сферой. Устойчивые течения $U_{1}^{{exp}}(x)$ и $U_{2}^{{exp}}(t,x)$ имеют несимметричные зоны закручивания.
Нестационарная система уравнений двадцатого порядка St2 (уравнение (1.4)) корректно воспроизводит процесс потери устойчивости течения в следе за сферой. Стационарное решение $\hat {\bar {С}}_{i}^{{(0)}},$ $i = 1,\,\,...,\,\,20,$ системы St2 корректно воспроизводит осесимметричную зону закручивания $U_{0}^{{exp}}(x)$ (рис. 1). Потеряв устойчивость, нестационарное решение Sol0 системы St2 не только сохраняет осевую симметрию, но и воспроизводит экспериментально наблюдаемые периодические осесимметричные пульсации зоны закручивания в следе за сферой, $V_{0}^{{exp}}(t,x)$ [18, 19].
Стационарное решение уравнений Навье–Стокса $U_{0}^{{NS}}(x)$ также успешно воспроизводит осесимметричную зону закручивания в следе за сферой $U_{0}^{{exp}}(x).$ Однако задача воспроизведения первого неустойчивого режима течения $V_{0}^{{exp}}(t,x)$ оказалась непосильной для решений уравнений Навье–Стокса. Потеряв устойчивость, решение $U_{0}^{{NS}}(x)$ испытало бифуркацию к стационарному неосесимметричному решению $U_{1}^{{NS}}(x).$ Потеря осевой симметрии, сопровождающая потерю устойчивости решением $U_{0}^{{NS}}(x),$ создает непреодолимую преграду для интерпретации наблюдаемых неустойчивых режимов в терминах решений уравнений классической гидродинамики [20, 21].
Оказалось, что в потерявшей устойчивость зоне закручивания каждое из отклонений от стационарного решения $\hat {\bar {C}}_{i}^{{(0)}},$ $i = 1,\,\,...,\,\,20,$ системы St2 повело себя во времени сугубо индивидуально. Перестало существовать некоторое среднее решение, пригодное для интерпретации всех изначально близких регулярных решений (рис. 2). Ансамбль Гиббса распался. Такое поведение решений называется эффектом бабочки Лоренца [14]. Потерявшее устойчивость решение системы St2 уже не может удовлетворить закону сохранения импульса. Для выполнения закона сохранения потребовался учет неупорядоченных возмущений, возникающих в среде за счет внешнего воздействия.
Список литературы
Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1987.
Townsend A.A. The structure of turbulent shear flow. Cambridge University Press, 1956.
Sakamoto H., Haniu H. // J. Fluid Mech. 1995. V. 287. P. 151.
Лебедь И.В., Уманский С.Я. // Хим. физика. 2012. Т. 31. № 2. С. 70.
Lebed I.V. The foundations of multimoment hydrodynamics. Pt. 1: ideas, methods and equations. N.Y.: Nova Science Publishers, 2018.
Lebed I.V. // Chem. Phys. Lett. 1990. V. 165. № 1–2. P. 226.
Лебедь И.В. // Хим. физика. 1995. Т. 14. № 5. С. 3.
Лебедь И.В. // Хим. физика. 1996. Т. 15. № 6. С. 64.
Лебедь И.В. // Хим. физика. 1996. Т. 15. № 12. С. 3.
Лебедь И.В. // Хим. физика. 1997. Т. 16. № 7. С. 72.
Лебедь И.В. // Хим. физика. 1998. Т. 17. № 3. С. 25.
Lebed I.V. // Open J. Fluid Dynam. 2014. V. 4. P. 163.
Glansdorff P., Prigogine I. Thermodynamic theory of structure, stability, and fluctuations. N.Y.: Willey, 1971.
Schuster H.G. Deterministic chaos. Weinheim: Physik Verlag, 1984.
Liboff R.L. Introduction to the theory of kinetic equations. N.Y.: Willey, 1969.
Ferziger J.H., Kaper H.G. Mathematical theory of transport processes in gases. Amsterdam: North-Holland Publishing Company, 1972.
Лифшиц Е.М., Питаевский Л.П. Статистическая физика Ч. 2. М.: Наука, 1978.
Taneda S. // J. Phys. Soc. Jpn. 1956. V. 11. № 10. P. 1104.
Chomaz J.M., Bonneton P., Hopfinger E.J. // J. Fluid Mech. 1993. V. 234. P. 1.
Лебедь И.В., Уманский С.Я. // Хим. физика. 2007. Т. 26. № 1. С. 65.
Лебедь И.В. // Хим. физика. 2014. Т. 33. № 4. С. 1.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика