Химическая физика, 2021, T. 40, № 1, стр. 24-29

ВВЕДЕНИЕ

Обеспечение устойчивого перехода волны горения через границу раздела малогазовых систем необходимо для решения важной практической задачи – сокращения времени переходного процесса и повышения предела горения многослойных систем [1]. Под областью устойчивого переходного процесса горения подразумевается область параметров, при которых переход волны горения через границу контакта завершается выходом на установившийся режим ее распространения по поджигаемому составу [1–4].

Теоретический и экспериментальный анализы зажигания волной горения для термитных составов на основе сопоставления “избытков энтальпий” ΔH (т.е. запасов тепла в зоне прогрева перед фронтом экзотермической реакции) был проведен в работах [1, 2], а для порохов и металлизированных гетерогенных составов – в [3, 4]. Аналитическое исследование режимов инициирования составных гетерогенных систем в предположении, что температура на границе раздела к моменту полного выгорания воспламенителя – известная величина, представлено в работе [5].

В работах [6, 7] предложены критерии для оценки устойчивости перехода фронта горения через границу раздела химически активных составов с различными теплофизическими параметрами. В [7] для анализа зажигания слоя многослойной системы волной горения использовался метод критического условия, который дает хорошие результаты при нарастающих тепловых потоках в поджигаемый состав. Исследования прохождения волны горения систем с конденсированными продуктами реакции через плоскую преграду с учетом ее толщины и теплофизических свойств проведены в [8, 9]. В работе [9] экспериментально исследовано влияние разрушающейся плоской инертной преграды на переход горения между слоями. Был сделан вывод, что срыв горения в переходной зоне зависит не только от энергокинетических параметров воспламенителя и поджигаемой системы, но и от тепловой активности преграды. В работах [10, 11] теоретически и экспериментально исследовано горение безгазовых систем, разделенных инертной газовой прослойкой. В [11] представлены приближенные критерии для оценки осуществимости переходного процесса для конденсированных составов с различными теплофизическими параметрами в условиях конкурирующих механизмов теплопередачи в газовом зазоре – кондуктивного и лучистого.

Нестационарный выход на установившийся волновой режим в поджигаемом слое в зависимости от формы преграды, внешних тнеплопотерь, теплофизических и энергокинетических параметров слоев является нетривиальной, ранее неисследованной задачей. Целью работы было изучение распространения волны горения по слоевой системе, состоящей из экзотермически реагирующих безгазовых конденсированных слоев, разделенных внедренной инертной преградой, имеющей клинообразную форму. С помощью двумерной математической модели проведен анализ динамики перехода волны горения между слоями через инертную преграду с учетом влияния геометрических характеристик элементов преграды и теплопотерь.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

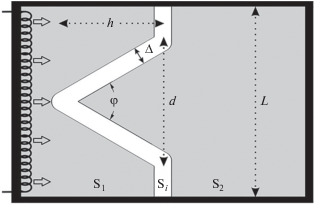
На рис. 1 представлена схема системы, состоящей из двух химически активных слоев, разделенных фигурной преградой. Преграда толщиной Δ имеет форму клина с “плечиками”, угол клина направлен навстречу фронту горения. Предполагалось, что как реагенты, так и продукты экзотермической реакции представляют собой конденсированные вещества и превращаются по безгазовому механизму. Двумерная нестационарная математическая модель описывает горение тонких слоев с конденсированными продуктами реакции. Для учета теплопотерь в окружающую среду с поверхности слоя вводится эффективный коэффициент теплообмена α. Распределением температуры по толщине слоя и теплопотерями через боковую поверхность пренебрегаем.

Рис. 1.

Схема модели для расчета переходных режимов горения через фигурную (“клиновидную”) преграду. Стрелками указано направление движения фронта горения от торца – места его инициирования.

Безразмерная система уравнений, описывающая горение химически активных слоев S₁ и S₂, разделенных преградой S_i, имеет следующий вид:

Уравнение теплопереноса для инертного слоя S_i:

Уравнения макрокинетики экзотермического превращения химически активных слоев:

Начальные условия для химически активных слоев S₁ и S₂ –

для инертного слоя S_i –

Граничные условия на боковой поверхности:

Инициирование горения осуществляется с торца слоя (граница области S₁) постоянным источником тепла при

На границе инициирующего химически активного и инертного слоев используются законы непрерывности потоков тепла и температуры:

Непрерывность потоков тепла и температуры на границе контакта инертного и второго химически активного слоев имеет вид

В приведенных выше уравнениях η – глубина превращения конденсированных реагентов, $\bar {n}$ – нормаль к границе преграды, θ – температура, $\;{{\theta }_{{ign}}}$ – температура инициирования, τ – время, ξ и ζ – пространственные переменные; γ, β, δ_i – параметры, связанные с размерными переменными и параметрами системы следующими соотношениями: ${{t}_{*}} = RT_{*}^{2}{{k}^{{ - 1}}}\exp {{\left( {{E \mathord{\left/ {\vphantom {E {R{{T}_{*}}}}} \right. \kern-0em} {R{{T}_{*}}}}} \right)c} \mathord{\left/ {\vphantom {{\left( {{E \mathord{\left/ {\vphantom {E {R{{T}_{*}}}}} \right. \kern-0em} {R{{T}_{*}}}}} \right)c} {QE}}} \right. \kern-0em} {QE}}$ – время, ${{x}_{*}} = {{\left[ {({\lambda \mathord{\left/ {\vphantom {\lambda {c\rho }}} \right. \kern-0em} {c\rho }}){{t}_{*}}} \right]}^{{0.5}}}$ – масштаб длины, ${{T}_{*}} = {{{{T}_{0}} + Q} \mathord{\left/ {\vphantom {{{{T}_{0}} + Q} c}} \right. \kern-0em} c}$ – характерная температура процесса,

Параметры: $\gamma = {{RT_{*}^{2}c} \mathord{\left/ {\vphantom {{RT_{*}^{2}c} {EQ}}} \right. \kern-0em} {EQ}}$ – отношение ширины зоны реакции к ширине зоны прогрева в волне горения в первом слое; $\beta = {{R{{T}_{*}}} \mathord{\left/ {\vphantom {{R{{T}_{*}}} E}} \right. \kern-0em} E}$ – температурная чувствительность скорости реакции; ${{T}_{0}}$ – начальная температура; R – универсальная газовая постоянная; k, E и Q – предэкспонент, энергия активация и тепловой эффект реакции; c_i, c, ρ_i, ρ, λ_i, λ – соответственно теплоемкости, плотности, коэффициенты теплопроводности инертного и реагирующих слоев; ${{\delta }_{{{\lambda }i}}} = {{{{\lambda }_{i}}} \mathord{\left/ {\vphantom {{{{\lambda }_{i}}} \lambda }} \right. \kern-0em} \lambda },$ α – коэффициент внешних теплопотерь. При проведении расчетов теплофизические характеристики слоев принимались постоянными.

Переход фронта горения через границу раздела составов в общем случае целесообразно рассматривать состоящим из нескольких этапов. Первый этап – приближение горения к преграде, при котором происходит тепловое взаимодействие фронта горения с инертной преградой и поджигаемым слоем. Второй этап – зажигание химически активного слоя за преградой. Третий этап – формирование и распространение установившегося фронта за преградой. Срыв горения может произойти на каждом из этапов (на первом и третьем этапах реализуется предел по горению, нa втором – предел по зажиганию).

При переходе горения между слоями форма преграды определяет направление вектора теплового потока от раскаленных продуктов горения в глубь поджигаемого слоя. При зажигании слоя через инертную преграду плотность теплового потока, передаваемая поджигаемому слою, зависит от геометрических параметров инертной преграды: формы и соотношения размеров ее элементов.

ЧИСЛЕННЫЙ АНАЛИЗ

Горение многослойной системы исследовалось в параметрической области устойчивого распространения горения в химически активных слоях [12, 13] без учета возможности формирования неоднородных волновых структур [14]. На переход волны горения между слоями могут оказать влияние и фазовые превращения в области контакта слоев [15]. Влияние фактора устойчивости горения к бесконечно малым возмущениям в данной работе не рассматривалось.

Переход горения через инертную преграду исследовался при постоянной длине основания d и варьируемом угле φ, а также при изменяющемся d и постоянной высоте клина $h = ({d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}){\text{ctg}}({\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-0em} 2})$ – все величины безразмерные. В первом случае угол острия клина изменялся в пределах значений $30^\circ \leqslant \varphi \leqslant 180^\circ ,$ во втором –

Теплофизические параметры слоев удовлетворяли условию ${{\lambda c\rho } \mathord{\left/ {\vphantom {{\lambda c\rho } {{{\lambda }_{i}}{{c}_{i}}{{\rho }_{i}}}}} \right. \kern-0em} {{{\lambda }_{i}}{{c}_{i}}{{\rho }_{i}}}} < 1,$ что соответствует переходу волны горения через преграду с высокой теплопроводностью и плотностью, например металлическую. При указанном соотношении параметров по мере приближения фронта реакции к преграде температура и скорость горения снижаются. Падение скорости тепловыделения в окрестности границы раздела может привести к срыву горения (потуханию) перед преградой. Зажигание слоя за преградой реализуется в индукционном режиме, прогрев поджигаемой системы за счет теплового потока от продуктов горения происходит фактически по законам инертного теплообмена.

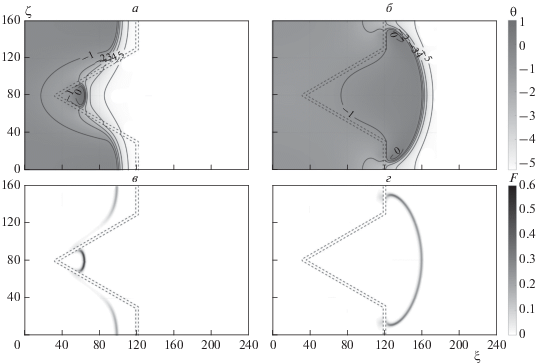
На рис. 2 представлены поля температуры θ и тепловыделения $F(\theta ,\eta )$ в различные моменты времени τ переходного процесса. Прогрев слоя после достижения фронтом горения преграды приводит к воспламенению в области S₂. За преградой в области острия клина формируется высокотемпературный фронт, распространяющийся в направлении основания клина (рис. 2а, в). Кривизна зоны реакции зависит от интенсивности и характера теплообмена с преградой и изменяется по ходу распространения горения.

Рис. 2.

Поля температуры θ (а, б) и тепловыделения F (в, г) в различные моменты времени. Параметры системы: β = = 0.1667, γ = 0.1894, θ₀ = –5.28, Δ = 3, δ_λi = 5, δ_i = 1.667, α = 1.5 ⋅ 10^–4, L = 160, d = 100, φ = 60°, τ = 800 для случаев а и в, τ = 1550 для случаев б и г.

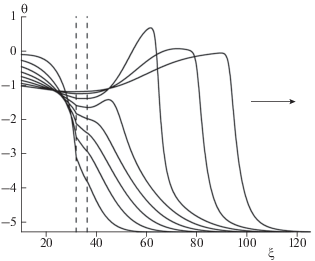
Для анализа перехода горения через инертную преграду на рис. 3 представлено одномерное пространственно-временное распределение температуры в осевом сечении клина. Вертикальные штриховые линии обозначают инертную преграду. Индукционный прогрев во время депрессии и аккумуляция энергии с учетом геометрического фактора приводят к резкому ускорению химической реакции за преградой и росту температуры горения до сверхадиабатических значений.

Рис. 3.

Пространственно-временное распределение температуры на оси клина (ζ = 80) для системы со следующими параметрами: β = 0.1667, γ = 0.1894, θ₀ = = –5.28, Δ = 3, δ_λi = 5, δ_i = 1.667, α = 1.5 ⋅ 10^–4, L = 160, d = 100, φ = 60°. Временной шаг между кривыми Δτ = 100. Стрелкой указано направление движения фронта.

По мере движения фронта горения в клине в силу геометрического фактора происходит постоянное увеличение оттока тепла из зоны реакции в зону прогрева, что приводит к уменьшению скорости распространения фронта. При выходе горения из клина формируется дугообразный фронт (рис. 2б, г). В дальнейшем горение распространяется по всей ширине образца L. При данных теплопотерях развитие горения за преградой приводит к формированию устойчивого плоского фронта.

Важным параметром, характеризующим переходный процесс горения, является время задержки зажигания, ${{\tau }_{{ign}}}$ – интервал времени от достижения нулевого градиента температуры за преградой до достижения значения глубины превращения $\eta = 0.5$ перед преградой.

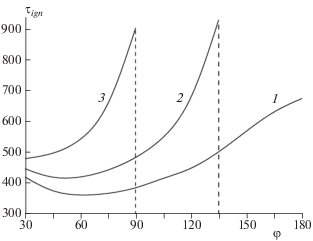
На рис. 4 представлена зависимость времени задержки зажигания ${{\tau }_{{ign}}}$ от угла клиновидной преграды φ при различных значениях теплопотерь α. Время ${{\tau }_{{ign}}}$ рассчитывалось для процесса горения в осевой части клина, так как именно здесь наблюдались первые вспышки за преградой. Численный анализ перехода горения за преграду проводился при постоянном значении основания клина d и ширине слоя L. В адиабатических условиях (рис. 4, кривая 1, α = 0) время задержки зажигания максимально при $\varphi = 180^\circ ,$ т.е. при переходе горения через плоскую преграду. При $\alpha = 1.5 \cdot {{10}^{{ - 4}}}$ и $\varphi > 135^\circ $ (кривая 2) или при $\alpha = 3.0 \cdot {{10}^{{ - 4}}}$ и $\varphi > 90^\circ $ (кривая 3) переход горения через преграду не реализуется.

Рис. 4.

Зависимости времени задержки зажигания τ_ign от угла φ при разных значениях теплопотерь: α = 0 (кривая 1), α = 1.5 ⋅ 10^–4 (кривая 2), α = 3 ⋅ 10^–4 (кривая 3). Параметры системы: β = 0.1667, γ = 0.1894, θ₀ = = –5.28, Δ = 3, δ_λi = 5, δ_i = 1.667, L = 160, d = 100.

Из численного анализа установлено, что для каждого угла φ существуют критические теплопотери ${{\alpha }_{{cr.i}}},$ при которых достигаются пределы по зажиганию слоя за преградой. Для углов φ, равных 30°, 60°, 90°, 120°, 150°, 180°, критические значения ${{\alpha }_{{cr.i}}}$ составили $4.7 \cdot {{10}^{{ - 4}}},$ $4.0 \cdot {{10}^{{ - 4}}},$ $3.0 \cdot {{10}^{{ - 4}}},$ $2.1 \cdot {{10}^{{ - 4}}},$ $1.5 \cdot {{10}^{{ - 4}}},$ $1.2 \cdot {{10}^{{ - 4}}}$ соответственно.

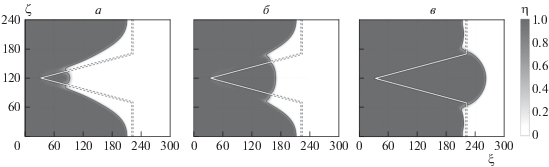
На рис. 5 представлены поля и изолинии глубины превращения η = 0.5, положение которых соответствует границам распространения экзотермической реакции при различных значениях α. Рисунок 5a соответствует случаю, когда зажигание внутри клина не завершилось распространением фронта горения. С уменьшением теплопотерь α срыв горения происходит на значительном расстоянии от острия клина (рис. 5б). Причина срыва в обоих случаях связана с изменением условий теплообмена с инертной преградой в процессе инициирования и распространения фронта горения в клине, расширением и изменением кривизны зоны реакции [16] и внешними теплопотерями. По той же причине происходит срыв пламени при выходе фронта горения из клина (рис. 5в). При дальнейшем уменьшении уровня теплопотерь α формируется устойчивый фронт горения в поджигаемом слое.

Рис. 5.

Поля глубины превращения после срыва горения для различных значений α. Изолиния соответствует значению η = 0.5. Параметры системы: β = 0.1667, γ = 0.1894, θ₀ = –5.28, Δ = 3, δ_λi = 5, δ_i = 1.667, L = 240, φ = 30°, α = = 5.328 ⋅ 10^–4 (а), 5.3275 ⋅ 10^–4 (б); 4.8 ⋅ 10^–4 (в).

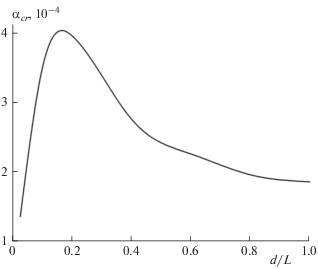
Критические теплопотери, связанные с зажиганием состава за преградой в области острия клина, ${{\alpha }_{{cr.i}}},$ и формированием фронта горения при выходе горения из клина, ${{\alpha }_{{cr}}},$ различаются при выбранных параметрах незначительно. Проведено численное исследование переходных процессов горения при изменении характерных размеров клина d и угла φ при постоянной высоте клина h. На рис. 6 представлена зависимость критических теплопотерь ${{\alpha }_{{cr}}}$ от отношения $d{\text{/}}L.$ Параметрическая область, ограниченная зависимостью ${{\alpha }_{{сr}}}(d{\text{/}}L),$ соответствует области устойчивого перехода горения через инертную преграду, т.е. теплопотерям, при которых после инициирования горения формируется фронт в поджигаемом слое. Существует оптимальное значение $d{\text{/}}L,$ при котором горение переходит через клинообразную преграду при максимальных значениях ${{\alpha }_{{cr}}}$ (см. рис. 6).

Рис. 6.

Зависимость критических значений теплопотерь α от отношения длины d “плеча” клиновидной преграды к ширине кюветы. Параметры системы: β = = 0.1667, γ = 0.1894, θ₀ = –5.28, Δ = 3, L = 600, h = 86.5.

Таким образом, сопоставление критических теплопотерь в переходном процессе горения для клинообразной и плоской преград свидетельствует об эффективности аккумуляции тепла для обеспечения выхода горения на установившийся волновой режим.

ЗАКЛЮЧЕНИЕ

Аккумуляция тепловой энергии с использованием инертной преграды клиновидного типа может применяться в безгазовых слоевых системах для повышения устойчивости переходных процессов горения плоских образцов и увеличения их устойчивости к теплопотерям во внешнюю среду. Численный анализ с помощью двумерной модели выявил зависимость параметров области устойчивого перехода горения через инертную преграду от ее геометрических характеристик. Существуют оптимальные геометрические характеристики инертной клиновидной преграды для устойчивого перехода безгазового горения между химически активными слоями.