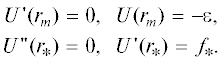Химическая физика, 2021, T. 40, № 12, стр. 3-17
Импульсная модель бимолекулярной рекомбинации тяжелых ионов
В. М. Азриель 1, В. М. Акимов 1, Е. В. Ермолова 1, Д. Б. Кабанов 1, Л. И. Колесникова 1, Л. Ю. Русин 1, *, М. Б. Севрюк 1
1 Федеральный исследовательский центр химической физики им. Н.Н. Семёнова
Российской академии наук
Москва, Россия
* E-mail: rusin@chph.ras.ru
Поступила в редакцию 31.05.2021
После доработки 10.06.2021
Принята к публикации 21.06.2021
Аннотация
Предложена импульсная модель бимолекулярной рекомбинации RM+ + X– → MX + R, где M+ – ион щелочного металла, X– – ион галогена, а R – нейтральный атом инертного газа или ртути. Проведены расчеты для M+ = Cs+, X– = Br–, R = Ar, Kr, Xe, Hg, энергий столкновения в диапазоне от 1 до 10 эВ и распределений внутренней энергии комплекса RM+, отвечающих температурам 500, 1000 и 2000 K. В импульсном приближении найдены функции возбуждения и функции прозрачности бимолекулярной рекомбинации и рассмотрена классификация столкновений по последовательностям попарных соударений частиц. В более чем половине всех случаев рекомбинация осуществляется за счет однократного удара иона Br– по атому R. Для рекомбинации XeCs+ + Br– импульсная модель позволяет воспроизвести важнейшие характеристики зависимости вероятности рекомбинации от энергии столкновения, полученные в рамках квазиклассических траекторных расчетов.
1. ВВЕДЕНИЕ
Реакции ионной диссоциации молекул и обратные реакции рекомбинации ионов являются важной составляющей многих сложных химических процессов, происходящих в различных неравновесных естественных или технологических средах. В частности, концентрация ионов в плазме определяется прежде всего конкуренцией указанных реакций [1, 2]. Простейшие примеры этих реакций – столкновительно-индуцированная диссоциация (СИД) двухатомных молекул на однозарядные ионы и рекомбинация однозарядных атомных ионов. Изучение процессов СИД занимает большое место в химической физике. Например, имеется обширная литература, посвященная исследованиям динамики ионной диссоциации молекул галогенидов щелочных металлов (прежде всего галогенидов цезия) в столкновениях с атомами инертных газов и ртути (а также с молекулой гексафторида серы) в скрещенных молекулярных пучках, см. обзоры [3–7] и подробную библиографию [8]. Эти реакции СИД протекают по схемам
где M+ – ион щелочного металла, X– – ион галогена, а R – нейтральный атом инертного газа или ртути. Канал СИД R + MX → RX– + M+ наблюдался в экспериментах со скрещенными молекулярными пучками только для системы Xe + CsI [9, 10]. Отметим, что галогениды цезия практически не диссоциируют на нейтральные атомы [11]. Основным средством теоретического изучения реакций (1) и (2) является квазиклассическое траекторное моделирование на адекватной поверхности потенциальной энергии (см. обзоры [4–7]).Экспериментальные исследования динамики реакций рекомбинации
обратных реакциям СИД (1) и (2), отсутствуют. Более того, экспериментальное изучение динамики прямой трехтельной рекомбинации (3) в настоящее время вообще не представляется возможным, что связано прежде всего с тем, что экспериментально осуществить пересечение трех достаточно интенсивных пучков или двух пучков и плотной газовой мишени чрезвычайно сложно. С другой стороны, различные динамические характеристики реакций (3) с M+ = Cs+ подробно исследованы в рамках метода квазиклассических траекторий [2, 7, 12–23]. В статье [22] приведены результаты квазиклассического траекторного моделирования одной из реакций (4), а именно, реакции XeCs+ + Br–. Отметим, что бимолекулярная реакция (4) является заключительной стадией одного из непрямых механизмов рекомбинации, известного как механизм связанного комплекса (bound complex mechanism) [2, 13, 24, 25].Моделирование элементарных атомно-молекулярных процессов в рамках метода квазиклассических траекторий, как правило, более наглядно, чем полуклассический или квантовомеханический расчет (и полностью оправдано, если все частицы, участвующие в процессе, достаточно тяжелые). Однако использование импульсных приближений иногда позволяет добиться еще большей наглядности в изучении атомно-молекулярных столкновений. В рамках импульсных моделей (моделей жестких сфер, hard sphere models) описание движения частиц в зоне сильного отталкивательного взаимодействия подвергается радикальному упрощению: эти частицы считаются шарами, которые при контакте обмениваются энергией и импульсом по закону упругого удара [4, 26–30] (иногда рассматриваются и неупругие соударения шаров). Кроме того, резко упрощено моделирование движения частиц вне зоны сильного отталкивательного взаимодействия. “Идеология” импульсного приближения, а также достоинства и недостатки импульсных моделей по сравнению с полным траекторным счетом подробно обсуждаются в работах [26–28, 31] и отчасти в работах [4, 32]. Первая попытка исследования химических реакций в импульсном приближении была, насколько известно авторам, предпринята в статье [33]. В отчете [28] приведен аннотированный список 209 работ (до 1991 г. включительно), в которых используется тот или иной вариант импульсного приближения для изучения различных явлений в химической или атомной физике. Импульсные модели реакций СИД (1) рассматривались во многих работах [4, 9, 10, 26, 28, 34–38]. Импульсные модели находят применение в теории атомно-молекулярных столкновений в газовой фазе вплоть до последнего времени [29–32, 39–43].
В работах [31, 32] предложена импульсная модель прямой трехтельной рекомбинации (3) и представлены результаты расчетов для реакций
(5)
${\text{C}}{{{\text{s}}}^{ + }} + {\text{B}}{{{\text{r}}}^{ - }} + {\text{R}} \to {\text{CsBr}} + {\text{R}}$(6)
${\text{RC}}{{{\text{s}}}^{ + }} + {\text{B}}{{{\text{r}}}^{ - }} \to {\text{CsBr}} + {\text{R}}$В случае СИД (2) модель должна включать тот или иной критерий образования молекулярного иона (комплекса) RM+. Различные варианты импульсной модели реакций (2) использовались в работах [4, 26, 45, 46] (см. также [10, 36]). Критерии образования молекулярного иона (в случае диссоциации молекулы соли MX) в этих работах сводятся, грубо говоря, к (возможно, неоднократной) проверке неравенства $W < \varepsilon ,$ где W – энергия относительного движения частиц R и M+, а $\varepsilon $ – глубина потенциальной ямы потенциала взаимодействия M+–R, т.е. энергия диссоциации комплекса. Выполнение неравенства $W < \varepsilon $ или какого-либо его аналога сразу после выхода системы из зоны сильного отталкивательного взаимодействия (т.е. непосредственно после прекращения серии упругих ударов между частицами R, M+, X–) является критерием формирования комплекса, а выполнение этого неравенства после разлета ионов в поле кулоновского потенциала на большое расстояние – критерием “выживания” комплекса. Импульсная модель реакций (2), включающая только критерий формирования комплекса, рассматривалась в работах [4, 26, 46], а импульсная модель, включающая оба критерия, – в работах [26, 45, 46].
Импульсная модель бимолекулярной рекомбинации (4), предложенная в настоящей статье, основана на следующем идеализированном представлении о сближении комплекса RM+ и иона X–. Обозначим через r межъядерное расстояние в комплексе. Реалистический потенциал $U(r)$ взаимодействия M+–R с $U( + \infty ) = 0$ характеризуется равновесным расстоянием ${{r}_{m}},$ глубиной $\varepsilon $ потенциальной ямы и расстоянием ${{r}_{*}} > {{r}_{m}},$ на котором сила притяжения между частицами R и M+ максимальна и равна ${{f}_{*}}{\text{:}}$
При $r = {{r}_{*}}$ график функции $U(r)$ имеет точку перегиба. В нашей модели предполагается, что комплекс RM+ и ион X– сближаются следующим образом: центр тяжести комплекса и ион X– движутся как две материальные точки соответствующих масс, связанные кулоновским притяжением, а атом R и ион M+ движутся вокруг центра тяжести комплекса как две материальные точки, связанные потенциалом $U(r)$ в отсутствие иона X–. Такое сближение комплекса RM+ и иона X– происходит до тех пор, пока расстояние d между центром тяжести комплекса и ионом X– не станет равным величине ${{d}_{*}},$ которая находится из уравнения (здесь и дальше, если не оговорено противное, используется атомная система единиц). Соотношение (7) означает, что сила кулоновского притяжения между комплексом RM+ и ионом X– равна максимальной силе притяжения между атомом R и ионом M+ в комплексе. После этого атом R начинает двигаться по инерции, а ионы M+ и X– – как два шара, связанные кулоновским притяжением. Потенциал $U(r)$ после достижения равенства $d = {{d}_{*}}$ уже не учитывается при рассмотрении движения частиц. Потенциал взаимодействия X––R мы не учитывали ни на каком этапе движения частиц.Прообразом такой модели является метод сопряженных (или склеенных) конических сечений (method of patched conics) в космодинамике [47–49]. В рамках этого метода пассивное (без тяги двигателей) движение космического аппарата C в поле тяготения двух небесных тел A и B масс ${{m}_{{\text{A}}}} < {{m}_{{\text{B}}}}$ (например, планеты и звезды́) рассматривается внутри так называемой сферы действия (sphere of influence) тела A как кеплерово относительно этого тела, а вне сферы действия тела A – как кеплерово относительно тела B. На границе сферы действия кеплеровы траектории “склеиваются” по достаточно простым правилам. Сама сфера действия тела A относительно тела B определяется как область местоположений космического аппарата C, где выполнено неравенство
Буквальный аналог метода сопряженных конических сечений для частиц R = A, X– = B и M+ = C при учете потенциала $U(r)$ взаимодействия M+–R = = C–A и кулоновского потенциала взаимодействия M+–X– = C–B выглядит следующим образом. Так как взаимодействием X––R = B–A мы пренебрегаем, то “сфера действия” атома R на ион M+ относительно иона X– совпадает со “сферой притяжения” и задается неравенством
где, как и выше, r – межъядерное расстояние M+–R, а s – межъядерное расстояние M+–X–. Внутри такой “сферы действия” ион M+ и атом R движутся вокруг общего центра тяжести как две материальные точки, связанные потенциалом $U(r).$ Вне “сферы действия” (8) ионы M+ и X– движутся вокруг общего центра тяжести как две материальные точки, связанные кулоновским притяжением.Отличия между нашей моделью и этим точным аналогом метода склеенных конических сечений состоят в следующем. В неравенстве (8) расстояние s между ионами мы заменяем на расстояние d между ионом X– и центром тяжести системы M+–R, а правую часть заменяем ее максимальным (при $r > {{r}_{m}}$) значением ${{f}_{*}}.$ Таким образом, уравнение “сферы действия” атома R на ион M+ относительно иона X– в нашей модели имеет вид ${{d}^{{ - 2}}} < {{f}_{*}}.$ Кроме того, когда ион M+ находится внутри такой “сферы действия”, мы считаем, что центр тяжести системы M+–R и ион X– движутся как пара материальных точек, связанных кулоновским притяжением.
2. ОПИСАНИЕ МОДЕЛИ
Как и в импульсной модели прямой трехтельной рекомбинации (5) [31, 32], каждая из частиц Cs+, Br–, Ar, Kr, Xe, Hg представлялась однородным шаром с массой, отвечающей реальному атомному весу соответствующего элемента. В качестве радиусов шаров использовались ионные радиусы ионов Cs+ и Br– (1.67 и 1.96 Å соответственно [50]) и атомные радиусы нейтральных атомов Ar, Kr, Xe, Hg (1.92 [51], 1.98 [52], 2.18 [52] и 1.55 Å [53] соответственно). Мы использовали те же потенциалы взаимодействия Cs+–R, что и в работах [2, 7, 12–23], посвященных траекторному моделированию рекомбинации (3) и (4) с M+ = Cs+.
Потенциалы взаимодействия Cs+–R с R = Ar, Kr, Xe задавались моделью [4, 34, 35]
(9)
$U(r) = A{{e}^{{{{ - r} \mathord{\left/ {\vphantom {{ - r} {{\rho }}}} \right. \kern-0em} {{\rho }}}}}} - {{{{\alpha }_{{\text{R}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{\text{R}}}}} {2{{r}^{4}}}}} \right. \kern-0em} {2{{r}^{4}}}} - {C \mathord{\left/ {\vphantom {C {{{r}^{6}}}}} \right. \kern-0em} {{{r}^{6}}}},$Потенциал взаимодействия Cs+–Hg мы, следуя работам [26, 38, 46], представляли как сумму потенциала взаимодействия изоэлектронной системы Xe–Hg (в форме Леннард-Джонса) и слагаемого ${{ - {{\alpha }_{{{\text{Hg}}}}}} \mathord{\left/ {\vphantom {{ - {{\alpha }_{{{\text{Hg}}}}}} {2{{r}^{4}}}}} \right. \kern-0em} {2{{r}^{4}}}},$ где ${{\alpha }_{{{\text{Hg}}}}} = 34.4$ а.е. [54] – поляризуемость атома ртути:
(10)
$U(r) = {{D}_{0}}[{{({{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} r}} \right. \kern-0em} r})}^{{12}}} - 2{{({{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} r}} \right. \kern-0em} r})}^{6}}] - {{{{\alpha }_{{{\text{Hg}}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{{\text{Hg}}}}}} {2{{r}^{4}}}}} \right. \kern-0em} {2{{r}^{4}}}}.$Значения всех параметров потенциалов (9) и (10) собраны в табл. 1 вместе с равновесным расстоянием ${{r}_{m}},$ глубиной $\varepsilon $ потенциальной ямы и расстояниями ${{r}_{*}}$ и ${{d}_{*}} = f_{*}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}$ (см. уравнение (7)). Отметим, что подробная аннотированная библиография работ (вплоть до 2016 г.) по потенциалам взаимодействия во всех двухчастичных системах M+–X–, M+–R, X––R и R–Hg (M+ – ион щелочного металла, X– – ион галогена, а R – атом инертного газа) приведена в отчете [64].
Таблица 1.
Параметры потенциалов взаимодействия Cs+–R (в атомной системе единиц)
| R | A | $\rho $ | C | ${{r}_{0}}$ | ${{D}_{0}}$ | ${{\alpha }_{{\text{R}}}}$ | ${{r}_{m}}$ | $\varepsilon $ | ${{r}_{ * }}$ | ${{d}_{ * }}$ |
|---|---|---|---|---|---|---|---|---|---|---|
| Ar | 450.19 | 0.51773 | 89 | – | – | 11.1 | 6.52 | 0.002702 | 7.354 | 33.3 |
| Kr | 796 | 0.5281 | 247.1 | – | – | 16.8 | 6.642 | 0.004448 | 7.478 | 25.8 |
| Xe | 318.5 | 0.6494 | 490 | – | – | 27.2 | 7.568 | 0.003987 | 8.578 | 29.72 |
| Hg | – | – | – | 7.75 | 0.0011 | 34.4 | 6.836 | 0.007588 | 7.651 | 20.1 |
Примечания. 1. То, что глубина потенциальной ямы $\varepsilon $ для системы Cs+–Xe меньше, чем для системы Cs+–Kr, может вызвать удивление, однако это неравенство согласуется с данными [60, 62] (см. также [58]). 2. В статье [21] мы использовали другие значения параметров A, $\rho $ и C для потенциала взаимодействия Cs+–Ar. 3. В работах [2, 13, 19, 38, 46] мы полагали ${{\alpha }_{{{\text{Hg}}}}} = 34$ а.е. [55].
Мы предполагали, что колебательные и вращательные уровни комплекса RM+ до сближения с ионом X– на критическое расстояние ${{d}_{*}}$ имеют больцмановские распределения, отвечающие некоторой температуре T. Процедура розыгрыша начальных условий столкновения реагентов RM+ и X– в нашей модели при фиксированной температуре T и энергии столкновения ${{E}_{{col}}}$ состояла в следующем.
В соответствии с краткой характеристикой модели, данной во введении, мы полагали, что в начальный момент времени $t = 0$ расстояние между центром тяжести комплекса RM+ и ионом X– равно ${{d}_{*}},$ а энергия относительного движения комплекса и иона равна ${{E}_{*}} = {{E}_{{col}}} + d_{*}^{{ - 1}}.$ Точнее, мы считали, что при $t = 0$ центр тяжести комплекса совпадает с началом неподвижной системы координат $xyz$ и имеет нулевую скорость, а ядро иона X– имеет координаты $\left( {{{{\left( {d_{*}^{2} - b_{*}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},{{b}_{*}},0} \right)$ и скорость $( - {{({{2{{E}_{*}}} \mathord{\left/ {\vphantom {{2{{E}_{*}}} {{{\mu }_{{col}}}}}} \right. \kern-0em} {{{\mu }_{{col}}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},0,0),$ где ${{\mu }_{{col}}}$ – приведенная масса комплекса RM+ и иона X–, а расстояние ${{b}_{*}} \leqslant {{d}_{*}}$ разыгрывается по правилу ${{b}_{*}} = {{d}_{*}}{{\xi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ (здесь $\xi $ – случайная величина, равномерно распределенная между 0 и 1). Из закона сохранения момента количества движения вытекает, что прицельный параметр b такого столкновения и расстояние ${{b}_{*}}$ связаны соотношением $bE_{{col}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} = {{b}_{*}}E_{*}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}},$ так что
(11)
$\begin{gathered} b = {{b}_{*}}{{({{{{E}_{*}}} \mathord{\left/ {\vphantom {{{{E}_{*}}} {{{E}_{{col}}}}}} \right. \kern-0em} {{{E}_{{col}}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{b}_{{max}}}{{\xi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ {{b}_{{max}}} = {{d}_{*}}{{({{{{E}_{*}}} \mathord{\left/ {\vphantom {{{{E}_{*}}} {{{E}_{{col}}}}}} \right. \kern-0em} {{{E}_{{col}}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $При прицельных параметрах, бо́льших ${{b}_{{max}}},$ рекомбинация в нашей модели невозможна. Отметим, что в подавляющем большинстве случаев при моделировании элементарных процессов значения прицельных параметров, при превышении которых данная реакция не реализуется, устанавливаются путем тестовых расчетов и не могут быть, строго говоря, указаны априори. Такая ситуация имеет место и для импульсной модели прямой трехтельной рекомбинации (3), предложенной в работах [31, 32]. В импульсной модели бимолекулярной рекомбинации (4), описанной в настоящей статье, предельное значение ${{b}_{{max}}}$ прицельного параметра вычисляется априори, хотя и через такую не имеющую явного физического смысла величину, как производная ${{f}_{ * }}$ потенциала взаимодействия в комплексе RM+ в точке перегиба (см. уравнение (7)). Когда энергия столкновения ${{E}_{{col}}}$ возрастает от нуля до бесконечности, коэффициент ${{({{{{E}_{*}}} \mathord{\left/ {\vphantom {{{{E}_{*}}} {{{E}_{{col}}}}}} \right. \kern-0em} {{{E}_{{col}}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ в (11) монотонно убывает от бесконечности до единицы, а значение ${{b}_{{max}}}$ монотонно убывает от бесконечности до ${{d}_{*}}.$
После определения ${{b}_{ * }}$ координаты и скорости иона M+ и атома R в комплексе RM+ при $t = 0$ разыгрывались, исходя из больцмановских распределений (при температуре T) колебательной энергии ${{E}_{{{v}ib}}} = \omega ({v} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})$ и вращательной энергии ${{E}_{{rot}}} = Bj(j + 1),$ где  B = $ = {{\left( {2{{\mu }_{{lex}}}r_{m}^{2}} \right)}^{{ - 1}}},$ ${{\mu }_{{lex}}}$ – приведенная масса иона M+ и атома R, а v и j – колебательное и вращательное квантовые числа. Иначе говоря, мы считали, что ${{E}_{{{v}ib}}}$ и ${{E}_{{rot}}}$ – это энергии гармонического осциллятора и жесткого ротатора соответственно с параметрами,
отвечающими потенциалу взаимодействия $U(r)$ в комплексе в окрестности точки минимума $r = {{r}_{m}},$ где $U(r) \approx {{{{\mu }_{{lex}}}{{\omega }^{2}}{{{(r - {{r}_{m}})}}^{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{{lex}}}{{\omega }^{2}}{{{(r - {{r}_{m}})}}^{2}}} {2 - \varepsilon }}} \right. \kern-0em} {2 - \varepsilon }}.$ Конечно, подобная процедура розыгрыша энергий ${{E}_{{{v}ib}}}$ и ${{E}_{{rot}}}$ не очень точна, особенно для потенциалов с такими “мелкими” потенциальными ямами,
как потенциалы взаимодействия M+–R, но связанная с этим погрешность заведомо меньше, чем погрешности самого́ импульсного
приближения. Если для данных значений v и j сумма энергий ${{E}_{{{v}ib}}} + {{E}_{{rot}}}$ превышала глубину $\varepsilon $ потенциальной ямы в комплексе, то такие значения v и j отвергались и колебательное и вращательное квантовые числа комплекса разыгрывались
снова. Весь розыгрыш состояния комплекса при $t = 0$ осуществлялся с помощью компьютерной программы, приведенной в отчете [65, стр. 59–61]
(с небольшими изменениями, связанными с необходимостью проверки неравенства ${{E}_{{{v}ib}}} + {{E}_{{rot}}} < \varepsilon $ и с другой формой потенциала).
B = $ = {{\left( {2{{\mu }_{{lex}}}r_{m}^{2}} \right)}^{{ - 1}}},$ ${{\mu }_{{lex}}}$ – приведенная масса иона M+ и атома R, а v и j – колебательное и вращательное квантовые числа. Иначе говоря, мы считали, что ${{E}_{{{v}ib}}}$ и ${{E}_{{rot}}}$ – это энергии гармонического осциллятора и жесткого ротатора соответственно с параметрами,
отвечающими потенциалу взаимодействия $U(r)$ в комплексе в окрестности точки минимума $r = {{r}_{m}},$ где $U(r) \approx {{{{\mu }_{{lex}}}{{\omega }^{2}}{{{(r - {{r}_{m}})}}^{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{{lex}}}{{\omega }^{2}}{{{(r - {{r}_{m}})}}^{2}}} {2 - \varepsilon }}} \right. \kern-0em} {2 - \varepsilon }}.$ Конечно, подобная процедура розыгрыша энергий ${{E}_{{{v}ib}}}$ и ${{E}_{{rot}}}$ не очень точна, особенно для потенциалов с такими “мелкими” потенциальными ямами,
как потенциалы взаимодействия M+–R, но связанная с этим погрешность заведомо меньше, чем погрешности самого́ импульсного
приближения. Если для данных значений v и j сумма энергий ${{E}_{{{v}ib}}} + {{E}_{{rot}}}$ превышала глубину $\varepsilon $ потенциальной ямы в комплексе, то такие значения v и j отвергались и колебательное и вращательное квантовые числа комплекса разыгрывались
снова. Весь розыгрыш состояния комплекса при $t = 0$ осуществлялся с помощью компьютерной программы, приведенной в отчете [65, стр. 59–61]
(с небольшими изменениями, связанными с необходимостью проверки неравенства ${{E}_{{{v}ib}}} + {{E}_{{rot}}} < \varepsilon $ и с другой формой потенциала).
Если для данного набора значений расстояния ${{b}_{*}}$ и координат и скоростей иона M+ и атома R при $t = 0$ расстояние между ядрами каких-либо двух частиц из M+, X–, R оказывалось меньше суммы радиусов этих частиц, то такой набор отвергался и начальные условия столкновения разыгрывались снова.
Итак, потенциал $U(r)$ взаимодействия M+–R в нашей процедуре розыгрыша начальных условий столкновения используется двояким образом: для определения расстояния ${{d}_{*}}$ и при розыгрыше координат и скоростей иона M+ и атома R.
Зная координаты иона X– при $t = 0,$ указанные выше, и координаты иона M+, можно найти начальное межъядерное расстояние ${{s}_{*}}$ между ионами. Сумма H начальной энергии относительного движения комплекса RM+ и иона X– (равной ${{E}_{{col}}} + d_{*}^{{ - 1}}$) и начальной энергии кулоновского взаимодействия ионов (равной $ - s_{*}^{{ - 1}}$) в нашей модели не обязательно равна ${{E}_{{col}}}$ и меняется от одного набора начальных условий к другому. Однако в среднем H мало отличается от ${{E}_{{col}}}.$ Действительно, положение иона M+ при $t = 0$ определяется его расстоянием ${{\ell }_{*}}$ до начала координат (центра тяжести комплекса) и положением на сфере с центром в начале координат и радиусом ${{\ell }_{*}}$, при этом плотность вероятности нахождения ядра иона M+ в любой точке сферы постоянна и равна ${{\left( {4\pi \ell _{*}^{2}} \right)}^{{ - 1}}}$ (если пренебречь тем условием, что шары, представляющие частицы M+, X–, R, не должны “перекрываться”). С другой стороны, расстояние от иона X– до начала координат при $t = 0$ всегда равно ${{d}_{*}},$ а внешнее электростатическое поле равномерно заряженной сферы такое же, как и у точечного заряда, равного полному заряду сферы и помещенного в центр сферы [66] (внутреннее электростатическое поле такой сферы равно нулю). Поэтому значение $ - s_{*}^{{ - 1}},$ усредненное по всем возможным положениям иона M+ с ${{\ell }_{*}} < {{d}_{*}},$ равно $ - d_{*}^{{ - 1}}.$
После определения начальных условий столкновения RM+ + X– дальнейшее моделирование движения частиц, как уже отмечалось во введении, проводилось в точности так же, как в импульсной модели прямой трехтельной рекомбинации (3) [31, 32]. Предполагалось, что при контакте любых двух шаров, представляющих частицы, их скорости мгновенно меняются по закону упругого удара [4, 26–30]. В промежутках между соударениями шаров атом R и центр тяжести ионной пары движутся по инерции, а относительное движение ионов мы определяли путем численного решения ньютоновых уравнений движения, отвечающих материальной точке в поле кулоновского потенциала на плоскости, перпендикулярной сохраняющемуся вектору момента количества движения ${\mathbf{L}} = {{\mu }_{{ion}}}[{\mathbf{s}},{\mathbf{\dot {s}}}]$ системы M+–X– (масса точки равна приведенной массе ионов ${{\mu }_{{ion}}};$ через ${\mathbf{s}}$ обозначен вектор, соединяющий ядра ионов).
Интегрирование уравнений движения проводилось методом Адамса–Башфорта (Adams–Bashforth) шестого порядка, при этом первые пять шагов интегрирования (после розыгрыша начальных условий или после очередного соударения двух частиц) выполнялись методом Рунге–Кутта (Runge–Kutta) четвертого порядка. Шаг интегрирования полагался равным 10 а.е., что оказалось достаточным для сохранения полной внутренней энергии ${{E}_{{tot}}} = {{{{\mu }_{{ion}}}{{{{\mathbf{\dot {s}}}}}^{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{{ion}}}{{{{\mathbf{\dot {s}}}}}^{2}}} 2}} \right. \kern-0em} 2} - {1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}$ и момента количества движения L ионной пары M+–X– между двумя последовательными соударениями с точностью до $ \approx 15$ значащих цифр. Момент удара определялся с помощью серии пробных одношаговых интегрирований уравнений движения назад методом Рунге–Кутта четвертого порядка. В статье [32] подробно объясняется, почему мы предпочли численное интегрирование уравнений движения аналитическому решению задачи Кеплера о движении материальной точки в кулоновском потенциале.
Интегрирование уравнений движения прекращалось и мы переходили к розыгрышу начальных условий следующего столкновения RM+ + X–, как только минимальное из двух межъядерных расстояний M+–R и X––R становилось больше 250 а.е. Если в этот момент времени полная внутренняя энергия ${{E}_{{tot}}}$ ионной пары оказывалась отрицательной, рекомбинация ионов M+ и X– считалась состоявшейся (независимо от текущего межъядерного расстояния s между ионами). Априорно минимально возможная энергия ${{E}_{{tot}}}$ отвечает неподвижным касающимся шарам, представляющим ионы M+ и X–, и в случае ионов Cs+ и Br– равна $ - 3.96684$ эВ.
Отметим, что при использовании импульсной модели следует четко различать столкновение (collision) частиц, под которым понимается весь процесс взаимодействия ионов M+ и X– и атома R от начального момента времени $t = 0$ до прекращения интегрирования уравнений движения, и попарные упругие соударения (encounters) частиц, которых в рамках одного акта столкновения может быть много. Соударение ионов между собой не влияет на полную внутреннюю энергию ${{E}_{{tot}}}$ ионной пары; энергия ${{E}_{{tot}}}$ может измениться только при соударении одного из ионов с атомом R.
3. РЕЗУЛЬТАТЫ РАСЧЕТОВ
Для каждого из четырех атомов R = Ar, Kr, Xe, Hg, для каждого из трех значений температуры $T = 500$, 1000, 2000 K и для каждого значения энергии столкновения ${{E}_{{col}}}$ от 1 до 10 эВ с шагом в 1 эВ мы разыграли $N = 500{\kern 1pt} 000$ столкновений RCs+ + Br–. Для каждого из 120 наборов $({\text{R}},T,{{E}_{{col}}})$ вероятность рекомбинации равна $P = {{{{N}_{0}}} \mathord{\left/ {\vphantom {{{{N}_{0}}} N}} \right. \kern-0em} N},$ где ${{N}_{0}}$ – число столкновений, заканчивающихся рекомбинацией ионов Cs+ и Br– (такие столкновения мы будем называть рекомбинационными). Из правила (11) розыгрыша прицельных параметров b столкновений вытекает, что сечение рекомбинации $\sigma $ можно вычислить по формуле
Стандартная ошибка (известная также как средняя ошибка или статистическая погрешность) вероятности P оценивается как ${{[{{P(1 - P)} \mathord{\left/ {\vphantom {{P(1 - P)} N}} \right. \kern-0em} N}]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ [67, 68].
Расчеты показывают, что динамика рекомбинации (6) в нашей модели слабо зависит от температуры T (т.е. от начальной внутренней энергии комплекса). Никакой тенденции возрастания или убывания вероятности рекомбинации P с увеличением температуры T мы не обнаружили. Для каждого из 40 наборов $({\text{R}},{{E}_{{col}}})$ обозначим через $\bar {P}$ среднее арифметическое трех значений P, полученных при $T = 500$, 1000 и 2000 K, а через $\Delta P$ – разность между максимальным и минимальным из этих трех значений. Отношение ${{\Delta P} \mathord{\left/ {\vphantom {{\Delta P} {\bar {P}}}} \right. \kern-0em} {\bar {P}}}$ не превышает 0.0238, 0.0196, 0.0374 и 0.0861 для R = Ar, Kr, Xe и Hg соответственно. Более того, отношение $\zeta = {{\Delta P} \mathord{\left/ {\vphantom {{\Delta P} {{{{[{{\bar {P}(1 - \bar {P})} \mathord{\left/ {\vphantom {{\bar {P}(1 - \bar {P})} N}} \right. \kern-0em} N}]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{{[{{\bar {P}(1 - \bar {P})} \mathord{\left/ {\vphantom {{\bar {P}(1 - \bar {P})} N}} \right. \kern-0em} N}]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}$ в наших вычислениях не превосходит 4.3 (а во многих случаях в несколько раз меньше); другими словами, разница в значениях вероятности P при разных температурах T находится в рамках статистической погрешности. Исключениями являются лишь случаи R = Hg, ${{E}_{{col}}} = 1$ эВ ($\zeta = 25.4$) и R = Hg, ${{E}_{{col}}} = 2$ эВ ($\zeta = 9.3$). Это, возможно, связано с тем, что расстояние ${{d}_{*}}$ для потенциала взаимодействия Cs+–Hg заметно меньше, чем для потенциалов взаимодействия Cs+–Ar, Cs+–Kr и Cs+–Xe (см. табл. 1).
Для каждого из четырех атомов R (и для каждого из трех значений температуры T) вероятность рекомбинации P и ее сечение $\sigma ,$ как и следовало ожидать, монотонно убывают с ростом энергии столкновения ${{E}_{{col}}}.$ На рис. 1 показаны зависимости вероятности рекомбинации P от ${{E}_{{col}}}$ при $T = 1000$ K, а на рис. 2 – зависимости сечения рекомбинации $\sigma $ от ${{E}_{{col}}}$ (т.е. функции возбуждения) при $T = 1000$ K. Благодаря наличию множителя ${{d}_{*}} + E_{{col}}^{{ - 1}}$ в формуле (12) сечение $\sigma $ уменьшается с ростом энергии ${{E}_{{col}}}$ несколько быстрее, чем вероятность P, что особенно заметно при малых ${{E}_{{col}}}.$ При $T = 1000$ K отношение
Рис. 1.
Зависимости вероятности P рекомбинации (6) от энергии столкновения ${{E}_{{col}}}$ при $T = 1000$ K. Кривые 1, 2, 3 и 4 отвечают R = Ar, Kr, Xe и Hg соответственно.

Рис. 2.
Функции возбуждения рекомбинации (6) при $T = 1000$ K. Кривые 1, 2, 3 и 4 отвечают R = Ar, Kr, Xe и Hg соответственно. Кривая 5 представляет (в относительных единицах) функцию возбуждения рекомбинации (6) с R = Xe, полученную в траекторном счете [22].

Представляет интерес сравнение вероятностей P бимолекулярной рекомбинации (6) и вероятностей ${{P}_{3}}$ трехтельной рекомбинации (5) в импульсном приближении. На рис. 3 показаны зависимости ${{P}_{3}}$ от энергии третьего тела ${{E}_{{\text{R}}}}$ при фиксированной энергии сближения ионов ${{E}_{{\text{i}}}} = 1$ эВ для импульсной модели [32] рекомбинации (5) в случае максимальных значений прицельных параметров ${{b}_{{\text{i}}}}$ и ${{b}_{{\text{R}}}},$ равных 80 и 40 а.е. соответственно. Для каждого из четырех атомов R (в особенности для R = Ar) зависимость ${{P}_{3}}$ от ${{E}_{{\text{R}}}}$ характеризуется более медленным уменьшением вероятности рекомбинации с ростом энергии, чем зависимость P от ${{E}_{{col}}}.$ Отношение
Рис. 3.
Зависимости вероятности ${{P}_{3}}$ трехтельной рекомбинации (5) от энергии третьего тела ${{E}_{{\text{R}}}}$ при фиксированной энергии сближения ионов ${{E}_{{\text{i}}}} = 1$ эВ для ${{b}_{{{\text{i}},max}}} = 80$ а.е. и ${{b}_{{{\text{R}},max}}} = 40$ а.е. в импульсном приближении [32]. Кривые 1, 2, 3 и 4 отвечают R = Ar, Kr, Xe и Hg соответственно.

Функции прозрачности реакций (6) в нашей модели, т.е. зависимости вероятности рекомбинации от прицельного параметра b при фиксированных значениях T и ${{E}_{{col}}},$ показаны на рис. 4 при $T = 1000$ K для минимальной (1 эВ) и максимальной (10 эВ) энергии столкновения ${{E}_{{col}}}.$ Эти функции прозрачности получены следующим образом: интервал $0 \leqslant b \leqslant {{b}_{{max}}}$ изменения параметра b делился на подынтервалы длины 1 а.е. (последний подынтервал был меньшей длины), значение функции прозрачности в центре данного подынтервала $\Xi $ равно отношению числа рекомбинационных столкновений, для которых b лежит в $\Xi ,$ к общему числу столкновений, для которых b лежит в $\Xi .$ Мелкие осцилляции на кривых рис. 4 вызваны статистическими погрешностями; отличие функций прозрачности при $T = 500$ и 2000 K от функций прозрачности при $T = 1000$ K не превышает этих погрешностей.
Рис. 4.
Функции прозрачности рекомбинации (6) при $T = 1000$ K. Кривые 1, 2, 3 и 4 отвечают R = Ar, Kr, Xe и Hg соответственно при ${{E}_{{col}}} = 1$ эВ. Кривые 5, 6, 7 и 8 отвечают R = Ar, Kr, Xe и Hg соответственно при ${{E}_{{col}}} = 10$ эВ.

Как видно из рис. 4, функции прозрачности для R = Kr, Xe и Hg в целом монотонно убывают с увеличением параметра b (если не считать небольшого начального участка возрастания при ${{E}_{{col}}} = 10$ эВ). Таково же поведение функций прозрачности для этих атомов R и при промежуточных значениях $2 \leqslant {{E}_{{col}}} \leqslant 9$ эВ энергии столкновения. С другой стороны, для са́мого легкого атома R = Ar (которому, кроме того, соответствует самое большое расстояние ${{d}_{*}},$ см. табл. 1) функция прозрачности при ${{E}_{{col}}} = 1$ эВ (а также при ${{E}_{{col}}} = 2$ эВ) характеризуется достаточно длинным начальным участком, где вероятность рекомбинации постоянна, а при ${{E}_{{col}}} = 10$ эВ (а также при $3 \leqslant {{E}_{{col}}} \leqslant 9$ эВ) – достаточно длинным начальным участком, где вероятность рекомбинации возрастает. Функции прозрачности реакции (6) с R = Xe, полученные в рамках траекторного моделирования, имеют совершенно другую форму. Например, траекторная функция прозрачности этой реакции при ${{E}_{{col}}} = 1$ эВ, изображенная на рис. 5 статьи [22], имеет резкий (хотя и “расщепленный”) максимум при $b \approx 20$ а.е.
Рис. 5.
Число различных типов столкновений RCs+ + + Br– среди $500{\kern 1pt} 000$ столкновений, разыгранных для данного атома R и данной энергии столкновения ${{E}_{{col}}}$ при $T = 1000$ K. Кривые 1, 2, 3 и 4 показывают число типов рекомбинационных столкновений для R = Ar, Kr, Xe и Hg соответственно. Кривые 5, 6, 7 и 8 показывают число типов нерекомбинационных столкновений для R = Ar, Kr, Xe и Hg соответственно.

Интересной особенностью рассматриваемой модели бимолекулярной рекомбинации (4) является то, что полная внутренняя энергия ${{E}_{{tot}}}$ ионной пары M+–X– может быть отрицательной уже в начальный момент времени $t = 0.$ В импульсной модели трехтельной рекомбинации (3) [31, 32] при энергиях сближения ионов ${{E}_{{\text{i}}}}$ порядка 1 эВ = = 0.03675 а.е. и выше это невозможно, потому что в [31, 32] начальное межъядерное расстояние между ионами равно ${{d}_{{\text{i}}}} = 250$ а.е., так что начальная полная внутренняя энергия ${{{{E}_{{\text{i}}}} - 1} \mathord{\left/ {\vphantom {{{{E}_{{\text{i}}}} - 1} {{{d}_{{\text{i}}}}}}} \right. \kern-0em} {{{d}_{{\text{i}}}}}}$ ионной пары всегда положительна. Конечно, неравенство ${{E}_{{tot}}}(t = 0) < 0$ в модели, предложенной в настоящей статье, не означает, что соответствующее столкновение обязательно является рекомбинационным: последующие соударения ионов с атомом R могут изменить знак ${{E}_{{tot}}}.$ В наших расчетах, относящихся к реакциям рекомбинации (6), нам встречались столкновения с ${{E}_{{tot}}}(t = 0) < 0$ только для R = Kr, Xe, Hg и только при ${{E}_{{col}}} \leqslant 3$ эВ. В табл. 2 указано число столкновений с ${{E}_{{tot}}}(t = 0) < 0$ для различных атомов R и разных значений температуры T и энергии столкновения ${{E}_{{col}}}.$
Таблица 2.
Число N0 столкновений RCs+ + Br– с Etot(t = 0) < 0 (из общего числа N = 500 000 всех столкновений), число N1 столкновений с Etot(t = 0) < 0 без соударений ионов с атомом R и число N2 столкновений с Etot(t = 0) < 0 вообще без соударений частиц (через точку с запятой приведены данные для Ecol = 1, 2 и 3 эВ)
| R | T, K | ${{N}_{0}}$ | ${{N}_{1}}$ | ${{N}_{2}}$ |
|---|---|---|---|---|
| Kr | 500 | 0; 0; 0 | 0; 0; 0 | 0; 0; 0 |
| 1000 | 2; 0; 0 | 1; 0; 0 | 1; 0; 0 | |
| 2000 | 1; 0; 0 | 1; 0; 0 | 0; 0; 0 | |
| Xe | 500 | 1; 0; 0 | 1; 0; 0 | 1; 0; 0 |
| 1000 | 10; 0; 0 | 9; 0; 0 | 3; 0; 0 | |
| 2000 | 11; 0; 0 | 7; 0; 0 | 3; 0; 0 | |
| Hg | 500 | 13 056; 6; 0 | 8646; 6; 0 | 6270; 0; 0 |
| 1000 | 19 383; 22; 3 | 13 233; 21; 3 | 9162; 7; 0 | |
| 2000 | 22 436; 29; 4 | 15 577; 26; 4 | 10 712; 9; 2 |
Как видно из табл. 2, для R = Kr и Xe мы наблюдали лишь единичные столкновения с Etot(t = = 0) < 0 (причем только при ${{E}_{{col}}} = 1$ эВ). В то же время для R = Hg число столкновений с ${{E}_{{tot}}}(t = 0) < 0$ при ${{E}_{{col}}} = 1$ эВ оказалось значительным даже для $T = 500$ K. Чтобы объяснить эту исключительную особенность ртути, оценим минимальное начальное межъядерное расстояние между ионом Cs+ и атомом R, при котором возможно неравенство ${{E}_{{tot}}}(t = 0) < 0$ (напомним, что ${{\mu }_{{ion}}},$ ${{\mu }_{{lex}}}$ и ${{\mu }_{{col}}}$ – это соответственно приведенная масса ионов, приведенная масса иона Cs+ и атома R и приведенная масса комплекса RCs+ и иона Br–). Будем считать, что энергия относительного движения иона Cs+ и атома R в комплексе RCs+ при $t = 0$ равна ${{E}_{T}} = {{k}_{B}}T,$ где ${{k}_{B}}$ – постоянная Больцмана. Скорость иона Br– при $t = 0$ в используемой нами системе координат равна ${{V}_{{{\text{Br}}}}} = {{({{2{{E}_{*}}} \mathord{\left/ {\vphantom {{2{{E}_{*}}} {{{\mu }_{{col}}}}}} \right. \kern-0em} {{{\mu }_{{col}}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ а скорость иона Cs+ равна ${{V}_{{{\text{Cs}}}}} = \lambda {{({{2{{E}_{T}}} \mathord{\left/ {\vphantom {{2{{E}_{T}}} {{{\mu }_{{lex}}}}}} \right. \kern-0em} {{{\mu }_{{lex}}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ где $\lambda $ – отношение масс ${{{{m}_{{\text{R}}}}} \mathord{\left/ {\vphantom {{{{m}_{{\text{R}}}}} {({{m}_{{\text{R}}}} + {{m}_{{{\text{Cs}}}}})}}} \right. \kern-0em} {({{m}_{{\text{R}}}} + {{m}_{{{\text{Cs}}}}})}}.$ Конечно, даже при ${{E}_{{col}}} = 1$ эВ и $T = 2000$ K энергия ${{E}_{T}}$ существенно меньше энергии ${{E}_{*}},$ а скорость ${{V}_{{{\text{Cs}}}}}$ – скорости ${{V}_{{{\text{Br}}}}}.$ Энергия относительного движения ионов при $t = 0$ не может быть меньше Ecrit = $ = {{{{\mu }_{{ion}}}{{{({{V}_{{{\text{Cs}}}}} - {{V}_{{{\text{Br}}}}})}}^{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{{ion}}}{{{({{V}_{{{\text{Cs}}}}} - {{V}_{{{\text{Br}}}}})}}^{2}}} 2}} \right. \kern-0em} 2},$ так что для реализации неравенства ${{E}_{{tot}}}(t = 0) < 0$ начальное межъядерное расстояние ${{s}_{*}}$ между ионами должно быть меньше ${{s}_{{crit}}} = {1 \mathord{\left/ {\vphantom {1 {{{E}_{{crit}}}}}} \right. \kern-0em} {{{E}_{{crit}}}}}$ (и при этом ${{s}_{{crit}}}$ должно быть не меньше суммы ${{s}_{0}}$ радиусов ионов, равной 6.85971 а.е.).
Начальное расстояние между центром тяжести комплекса RCs+ и ионом Br– равно ${{d}_{*}}.$ Поэтому для реализации неравенства ${{E}_{{tot}}}(t = 0) < 0$ начальное межъядерное расстояние между ионом Cs+ и атомом R должно быть больше величины ${{r}_{{crit}}},$ которая находится из уравнения $\lambda {{r}_{{crit}}} + {{s}_{{crit}}} = {{d}_{*}},$ т.е. больше величины ${{r}_{{crit}}} = {{({{d}_{*}} - {{s}_{{crit}}})} \mathord{\left/ {\vphantom {{({{d}_{*}} - {{s}_{{crit}}})} \lambda }} \right. \kern-0em} \lambda }.$ Простые вычисления показывают, что от температуры T значения ${{s}_{{crit}}}$ и ${{r}_{{crit}}}$ зависят мало, причем расстояние ${{s}_{{crit}}}$ мало зависит и от атома R. Так, при ${{E}_{{col}}} = 1$ эВ и $T = 1000$ K расстояние ${{s}_{{crit}}}$ равно 18.84, 18.48, 21.64 и 18.57 а.е. для R = Ar, Kr, Xe и Hg соответственно. Но для R = Hg расстояние ${{d}_{*}}$ заметно меньше, чем для трех других атомов R (см. табл. 1), а отношение $\lambda ,$ наоборот, больше. В силу этого расстояние ${{r}_{{crit}}}$ при ${{E}_{{col}}} = 1$ эВ для R = Hg оказывается малым (например, при $T = 1000$ K оно равно 2.54 а.е.), а для R = Ar, Kr, Xe – довольно значительным: при $T = 1000$ K оно равно 62.56, 18.92, 16.27 а.е. соответственно (начальное межъядерное расстояние между ионом Cs+ и атомом Ar, превышающее 62.56 а.е., разумеется, неосуществимо). С другой стороны, уже при ${{E}_{{col}}} = 2$ эВ расстояние ${{r}_{{crit}}}$ для R = Hg становится существенно больше; так, при $T = 1000$ K получаем ${{s}_{{crit}}} = 12.56$ а.е. и ${{r}_{{crit}}} = 12.54$ а.е. Мы наблюдали большое количество столкновений с Etot(t = 0) < 0 только для R = Hg и ${{E}_{{col}}} = 1$ эВ (см. табл. 2) именно потому, что это единственная пара $({\text{R}},{{E}_{{col}}}),$ характеризующаяся малыми расстояниями ${{r}_{{crit}}}.$
4. ТИПЫ СТОЛКНОВЕНИЙ
Для каждого акта столкновения RM+ + X– импульсная модель позволяет однозначно определить последовательность попарных соударений шаров, представляющих частицы M+, X– и R. Считая ион M+ первой частицей, ион X– – второй, а атом R – третьей, каждое такое соударение мы будем кодировать одним из шести чисел 12, ‒12, 13, –13, 23 и –23 по следующему правилу [31, 32]: соударение частицы № i и частицы № j (где $j > i$) обозначается одним из чисел $ \pm (10i + j),$ а знак числа совпадает со знаком полной внутренней энергии ${{E}_{{tot}}}$ ионной пары после соударения. Как уже отмечалось в конце разд. 2, соударения вида ±12 значение ${{E}_{{tot}}}$ не меняют.
В рамках рекомбинационного столкновения после всех соударений атома R с ионами остается связанная ионная пара M+–X–. Параметры эллипса, который при этом описывает вектор ${\mathbf{s}},$ соединяющий ядра ионов, легко вычисляются по энергии ${{E}_{{tot}}} < 0$ и моменту количества движения L ионной пары [48, 49]. Обозначим через ${{s}_{{{\pi }}}}$ радиус перицентра эллипса (минимальное расстояние от точки эллипса до его фокуса), а через ${{s}_{0}}$ – сумму радиусов шаров, представляющих ионы. В зависимости от того, какое из двух неравенств ${{s}_{{{\pi }}}} > {{s}_{0}}$ или ${{s}_{{{\pi }}}} < {{s}_{0}}$ выполнено, в изолированной связанной ионной паре M+–X– либо соударений ионов между собой вообще не происходит, либо же ионы испытывают бесконечно много соударений вида –12. В наших расчетах, относящихся к реакциям рекомбинации (6), до прекращения интегрирования уравнений движения в соответствии с алгоритмом разд. 2 успевало произойти лишь конечное число (обычно не превышающее десятка) таких соударений вида –12. Наибольшее количество подобных финальных соударений вида –12 мы наблюдали для одного из столкновений KrCs+ + Br– при $T = 1000$ K и ${{E}_{{col}}} = 1$ эВ. В этом рекомбинационном столкновении после двух соударений вида 12 и –23 до прекращения интегрирования уравнений движения произошло 892 соударения ионов между собой. В рамках нерекомбинационного столкновения после всех соударений атома R с ионами возможно еще одно соударение ионов между собой вида 12.
Как и в импульсной модели трехтельной рекомбинации (5) [31, 32], мы будем сопоставлять каждому столкновению RCs+ + Br– последовательность чисел, кодирующих попарные соударения частиц, не учитывая при этом финальные соударения ионов между собой (происходящие после всех соударений атома R с ионами). Получившуюся последовательность чисел, заключенную в круглые скобки, назовем типом столкновения. Например, столкновение типа (12, –23) является рекомбинационным и включает соударение ионов между собой с ${{E}_{{tot}}} > 0,$ соударение иона Br– с атомом R, меняющее знак энергии ${{E}_{{tot}}},$ и, возможно, еще несколько соударений ионов между собой вида –12 (как в упомянутом выше столкновении KrCs+ + Br– с 894 соударениями частиц). Рекомбинационные столкновения, не включающие ни одного соударения атома R с ионами, образуют отдельный тип, который мы будем условно обозначать как $( - \Omega )$. Для таких столкновений ${{E}_{{tot}}}(t = 0) = {{E}_{{tot}}}(t = {{t}_{{end}}}) < 0;$ они либо вообще не включают соударений частиц, либо включают несколько соударений вида –12 (${{t}_{{end}}}$ обозначает момент прекращения интегрирования уравнений движения). Числа ${{N}_{1}}$ в предпоследнем столбце табл. 2 – это количества столкновений типа $( - \Omega )$ в наших расчетах для разных наборов $({\text{R}},T,{{E}_{{col}}}).$ В импульсной модели трехтельной рекомбинации (5) [31, 32] столкновений типа $( - \Omega )$ мы не встречали (см. объяснение в конце разд. 3). Нерекомбинационные столкновения, не включающие ни одного соударения атома R с ионами, мы будем относить к типу $(\Omega ).$ Для таких столкновений ${{E}_{{tot}}}(t = 0) = {{E}_{{tot}}}(t = {{t}_{{end}}}) > 0;$ они либо вообще не включают соударений частиц, либо включают единственное соударение вида 12.
Самый “длинный” тип, который нам встретился, представлял собой последовательность 58 чисел 13. Мы наблюдали единственное столкновение такого типа. Это было одно из нерекомбинационных столкновений KrCs+ + Br– при $T = 1000$ K и ${{E}_{{col}}} = 1$ эВ. Оно включало 58 соударений иона Cs+ с атомом Kr без финального соударения ионов Cs+ и Br–.
В рамках импульсного моделирования прямой трехтельной рекомбинации (5) мы наблюдали 34 типа рекомбинационных столкновений (все эти типы перечислены в [31, 32]) и 61 тип нерекомбинационных столкновений (эти типы перечислены в [31]). В импульсной модели бимолекулярной рекомбинации (6), описанной в настоящей статье, мы встретили существенно больше различных типов столкновений.
Общее число актов столкновения RCs+ + Br– в наших вычислениях было равно 4 × 3 × 10 × $ \times \,\,500{\kern 1pt} 000 = 6 \cdot {{10}^{7}};$ здесь учтены четыре разных атома R, три значения температуры T и десять значений энергии ${{E}_{{col}}}.$ Из этих $6 \cdot {{10}^{7}}$ столкновений рекомбинационными оказались ${\text{1}}{\kern 1pt} {\text{863}}{\kern 1pt} {\text{030}}$ столкновений (3.10505%) 64 различных типов. Число типов нерекомбинационных столкновений в наших расчетах было равно 172 – в 2.6875 раза больше, чем число типов рекомбинационных столкновений. Впрочем, такое “разнообразие” типов бимолекулярных столкновений обеспечивается в значительной степени за счет очень небольшого числа столкновений (как рекомбинационных, так и нерекомбинационных), включающих длинные серии соударений вида 13, т.е. соударений иона Cs+ с атомом R, оставляющих положительной полную внутреннюю энергию ${{E}_{{tot}}}$ ионной пары. В рамках таких столкновений частицы Cs+ и R, вначале составлявшие комплекс RCs+, еще на протяжении некоторого времени испытывают много соударений между собой под влиянием иона Br–, притягивающего ион Cs+. По-видимому, атом R при этом оказывается “зажатым” между ионами. Подчеркнем, что такие столкновения очень редки. Мы встретили всего 4725 столкновений (66 рекомбинационных и 4659 нерекомбинационных), типы которых начинаются с пяти или более чисел 13, однако эти столкновения распределяются по 16 рекомбинационным и 53 нерекомбинационным типам. Еще у 9 нерекомбинационных столкновений тип заканчивается пятью или более числами 13, причем эти столкновения распределяются по семи различным типам.
В табл. 3 перечислены двадцать наиболее часто встречающихся типов рекомбинационных столкновений (в порядке убывания числа столкновений, относящихся к данному типу). Эти 20 типов покрывают 99.9204% всех рекомбинационных столкновений. Подавляющее большинство (69.9872%) рекомбинационных столкновений относится к типам (–23) и (13, –23). В рамках этих столкновений полная внутренняя энергия ${{E}_{{tot}}}$ ионной пары становится отрицательной за счет соударения атома R с ионом Br–, причем этому соударению может предшествовать соударение атома R с ионом Cs+, оставляющее энергию ${{E}_{{tot}}}$ положительной. В импульсной модели прямой трехтельной рекомбинации (5) [31, 32] двумя наиболее часто встречающимися типами рекомбинационных столкновений были (–23) и (–13), а тип (13, –23) был лишь на третьем месте. В импульсной модели бимолекулярной рекомбинации (6), как видно из табл. 3, мы также наблюдали рекомбинационные столкновения типа (–13), но этот тип стои́т по частоте встречаемости на 11‑м месте. Так как при $t = 0$ частицы Cs+ и R составляют комплекс RCs+, их относительная скорость мала (и остается не очень большой еще в течение какого-то времени), так что единичное соударение между атомом R и ионом Cs+ с высокой вероятностью лишь мало меняет скорость иона Cs+ и оставляет знак энергии ${{E}_{{tot}}}$ неизменным.
Таблица 3.
Двадцать наиболее часто встречающихся типов рекомбинационных столкновений
| Число столкновений | В % | Тип |
|---|---|---|
| 1 083 402 | 58.1527 | (–23) |
| 220 481 | 11.8345 | (13, –23) |
| 178 398 | 9.5757 | (12, –13) |
| 151 216 | 8.1167 | (–23, –13) |
| 60 194 | 3.2310 | (13, –23, –13) |
| 42 661 | 2.2899 | (23, –13) |
| 37 535 | 2.0147 | $( - \Omega )$ |
| 35 487 | 1.9048 | (12, –23) |
| 16 214 | 0.8703 | (13, 12, –13) |
| 11 002 | 0.5905 | (13, 23, –13) |
| 8898 | 0.4776 | (–13) |
| 6122 | 0.3286 | (–12, –13) |
| 2947 | 0.1582 | (13, 12, –23) |
| 2348 | 0.1260 | (–23, –13, –23) |
| 1559 | 0.0837 | (13, –23, –13, –23) |
| 1246 | 0.0669 | (13, 13, –23, –13) |
| 754 | 0.0405 | (13, 13, –23) |
| 487 | 0.0261 | (–13, –23) |
| 353 | 0.0189 | (23, –13, –23) |
| 243 | 0.0130 | (–12, –23) |
Двадцать наиболее часто встречающихся типов нерекомбинационных столкновений перечислены в табл. 4 (снова в порядке убывания числа столкновений, относящихся к данному типу). Эти 20 типов покрывают 99.9709% всех нерекомбинационных столкновений. Три самых частых типа нерекомбинационных столкновений – это те же типы $(\Omega ),$ (13), (23), что и в случае импульсной модели прямой трехтельной рекомбинации (5) [31, 32] (впрочем, доли встречаемости этих типов в импульсной модели трехтельной рекомбинации были совсем другими). Вместе эти три типа охватывают 94.8824% всех нерекомбинационных столкновений.
Таблица 4.
Двадцать наиболее часто встречающихся типов нерекомбинационных столкновений
| Число столкновений | В % | Тип |
|---|---|---|
| 39 249 419 | 67.5120 | $(\Omega )$ |
| 14 471 835 | 24.8927 | (13) |
| 1 440 518 | 2.4778 | (23) |
| 1 040 504 | 1.7897 | (12, 13) |
| 606 526 | 1.0433 | (23, 13) |
| 288 572 | 0.4964 | (13, 13) |
| 249 744 | 0.4296 | (13, 23) |
| 203 080 | 0.3493 | (12, 23) |
| 172 042 | 0.2959 | (13, 23, 13) |
| 146 189 | 0.2515 | (–23, 13) |
| 125 150 | 0.2153 | (13, 12, 13) |
| 41 349 | 0.0711 | (13, –23, 13) |
| 25 024 | 0.0430 | (13, 12, 23) |
| 24 355 | 0.0419 | (13, 13, 13) |
| 12 004 | 0.0206 | (23, 13, 23) |
| 6746 | 0.0116 | (13, 23, 13, 23) |
| 6020 | 0.0104 | (13, 13, 13, 13) |
| 4081 | 0.0070 | (–23, 13, 23) |
| 3576 | 0.0062 | (–23, –13, 23) |
| 3324 | 0.0057 | (–12, 13) |
Если от всего массива $6 \cdot {{10}^{7}}$ столкновений, разыгранных в наших расчетах, перейти к $500{\kern 1pt} 000$ столкновений, разыгранных для отдельных наборов $({\text{R}},T,{{E}_{{col}}}),$ то для некоторых наборов пара наиболее часто встречающихся типов рекомбинационных столкновений и тройка наиболее часто встречающихся типов нерекомбинационных столкновений будут другими.
Для всех наборов $({\text{R}},T,{{E}_{{col}}})$ самым частым типом рекомбинационных столкновений является тип (–23). Однако для R = Ar и ${{E}_{{col}}} = 10$ эВ при всех трех значениях температуры T, а также для R = Ar, $T = 1000$ K и ${{E}_{{col}}} = 9$ эВ вторым по частоте оказывается тип (23, –13), а тип (13, –23) переходит на третье место. Для R = Hg тип (13, –23) никогда не занимает второго места и отодвигается на третье, четвертое или пятое место в зависимости от T и ${{E}_{{col}}}.$ На втором же месте для R = Hg почти всегда стои́т тип (12, –13). Исключениями являются два набора $({\text{Hg}},T,\,\,1\,\,{\text{эВ}})$ с $T = 1000$ и 2000 K, для этих наборов вторым по частоте типом рекомбинационных столкновений оказывается тип $( - \Omega ).$ Отметим вероятную причину этой особенности ртути. Как объясняется в конце разд. 3, для R = Hg возможны меньшие начальные межъядерные расстояния ${{s}_{*}}$ между ионами, чем для R = Ar, Kr и Xe. По-видимому, в силу этого для ртути имеет больше шансов реализоваться следующий сценарий. Первым соударением частиц является соударение ионов между собой вида 12, которое сохраняет энергию ${{E}_{{tot}}}$, но сильно меняет скорости обоих ионов, так что скорость частиц R и Cs+ начинает заметно различаться. Затем происходит соударение этих частиц между собой, которое опять-таки сильно меняет их скорости (в частности, скорость иона Cs+), и энергия ${{E}_{{tot}}}$ становится отрицательной, т.е. соударение R и Cs+ оказывается соударением вида –13.
Самым частым типом нерекомбинационных столкновений для всех наборов $({\text{R}},T,{{E}_{{col}}})$ является тип $(\Omega )$, а вторым по частоте – тип (13). В то же время для 24 наборов $({\text{R}},T,{{E}_{{col}}})$ с низкими энергиями столкновения ${{E}_{{col}}} \leqslant 4$ эВ тип (23) оказывается не третьим по частоте, а четвертым, пятым или даже шестым. На третьем же месте для этих наборов стоя́т типы (12, 13) или (13, 13). Для других 24 наборов $({\text{R}},T,{{E}_{{col}}})$ с ${{E}_{{col}}} \leqslant 4$ эВ тип (23) занимает третье место.
Число ${{n}_{1}}$ различных типов рекомбинационных и число ${{n}_{2}}$ различных типов нерекомбинационных столкновений среди $500{\kern 1pt} 000$ столкновений, разыгранных для каждого набора $({\text{R}},T,{{E}_{{col}}}),$ мало зависят от температуры T и в целом уменьшаются с ростом энергии столкновения ${{E}_{{col}}}.$ На рис. 5 показаны зависимости этих чисел от ${{E}_{{col}}}$ при $T = 1000$ K. Отношение ${{{{n}_{2}}} \mathord{\left/ {\vphantom {{{{n}_{2}}} {{{n}_{1}}}}} \right. \kern-0em} {{{n}_{1}}}}$ для всех наборов $({\text{R}},T,{{E}_{{col}}})$ лежит в интервале от 1.416 до 3.75, в частности, для любого набора число типов нерекомбинационных столкновений больше числа типов рекомбинационных столкновений. В целом, как видно из рис. 5, больше всего типов как рекомбинационных, так и нерекомбинационных столкновений наблюдается для R = Kr, далее идут Ar, Xe и Hg.
5. ЗАКЛЮЧЕНИЕ
Как показали проведенные вычисления, предложенная импульсная модель реакций бимолекулярной рекомбинации (6) позволяет воспроизвести важнейшую черту динамики этих реакций – убывание вероятности и сечения рекомбинации с ростом энергии столкновения, причем убывание более быстрое, чем убывание вероятности трехтельной рекомбинации (5) с ростом энергии третьего тела при фиксированной энергии сближения ионов. С другой стороны, импульсные функции прозрачности реакций (6) с R = Xe сильно отличаются от функций прозрачности, полученных при траекторных расчетах [22].
Другими значимыми динамическими аспектами реакций рекомбинации (3) и (4) являются распределения продукта MX по колебательным и вращательным энергиям, а также минимально возможная полная внутренняя энергия продукта, характеризующая (в случае трехтельной рекомбинации) эффективность третьего тела R как акцептора избыточной энергии ионной пары [7, 14, 17, 19, 20, 40]. Однако в рамках импульсных моделей реакций (3) и (4), предложенных в работах [31, 32] и в настоящей статье, продуктом реакции считается не молекула соли MX, а пара ионов M+ и X–, связанная кулоновским потенциалом. Для такой пары полная внутренняя энергия ${{E}_{{tot}}}$ отрицательна, но полуоси эллипса, который описывает вектор ${\mathbf{s}},$ соединяющий ядра ионов, могут быть сколь угодно больши́ми. Поэтому рассматривать распределение энергии ${{E}_{{tot}}},$ раскладывать ${{E}_{{tot}}}$ на колебательную и вращательную компоненты и вычислять минимально возможное значение ${{E}_{{tot}}}$ при импульсном моделировании реакций (3) и (4) не имеет особого смысла.
В то же время одной из целей использования импульсных моделей в теории атомно-молекулярных столкновений является отделение эффектов масс частиц от эффектов структуры поверхностей потенциальной энергии (ППЭ) [4, 26–28, 31, 40]. Результаты настоящей статьи дают основание предполагать, что энергетические зависимости вероятностей трехтельной и бимолекулярной рекомбинации в существенно меньшей степени, чем особенности функций прозрачности, связаны с рельефом ППЭ. Для более подробного исследования этого вопроса необходимо проведение траекторного моделирования реакций (6) с R = Ar, Kr, Hg, а также расчеты в рамках импульсной модели с варьированием деталей потенциалов взаимодействия Cs+–R (а также при формальном изменении масс и радиусов частиц, ср. [19–21]).
Построение импульсных моделей прямой трехтельной рекомбинации ионов (3) в работах [31, 32] и бимолекулярной рекомбинации ионов (4) в настоящей статье позволяет предположить, что импульсные представления могут быть использованы при описании таких сложных рекомбинационных процессов, как реакции ион-ионной рекомбинации в атмосфере [69, 70], гибель атомов кислорода в атмосфере в результате рекомбинации с участием молекул O2 и N2 в качестве третьих тел [71] или рекомбинация радикалов в полимерной “клетке” и в объеме полимеров [72].
Работа выполнена в рамках темы “Фундаментальные физико-химические процессы воздействия энергетических объектов на окружающую среду и живые системы” Программы фундаментальных научных исследований государственных академий наук. Регистрационный номер темы в ЦИТиС АААА-А20-120011390097-9.
Список литературы
Князев Б.А. Низкотемпературная плазма и газовый разряд. Новосибирск: Изд-во НГУ, 2003.
Азриель В.М. Дис. … д-ра физ.-мат. наук. М.: ИНЭПХФ РАН, 2008.
Wexler S., Parks E.K. // Annu. Rev. Phys. Chem. 1979. V. 30. P. 179; https://doi.org/10.1146/annurev.pc.30.100179.001143
Маергойз А.И., Никитин Е.Е., Русин Л.Ю. // Химия плазмы. Вып. 12 / Под ред. Смирнова Б.М. М.: Энергоатомиздат, 1985. С. 3.
Rusin L.Yu. // J. Chem. Biochem. Kinetics. 1991. V. 1. № 3. P. 205.
Русин Л.Ю. // Изв. АН. Энергетика. 1997. № 1. С. 41.
Азриель В.М., Акимов В.М., Ермолова Е.В. и др. // Прикл. физика и математика. 2018. № 2. С. 30.
Русин Л.Ю., Севрюк М.Б., Акимов В.М., Кабанов Д.Б. Отчет в ЦИТиС. Рег. номер АААА-Б16-216100670036-8. М.: ИНЭПХФ РАН им. В.Л. Тальрозе, 2016.
Parks E.K., Inoue M., Wexler S. // J. Chem. Phys. 1982. V. 76. № 3. P. 1357; https://doi.org/10.1063/1.443129
Parks E.K., Pobo L.G., Wexler S. // Ibid. 1984. V. 80. № 10. P. 5003; https://doi.org/10.1063/1.446523
Ewing J.J., Milstein R., Berry R.S. // Ibid. 1971. V. 54. № 4. P. 1752; https://doi.org/10.1063/1.1675082
Азриель В.М., Кабанов Д.Б., Колесникова Л.И., Русин Л.Ю. // Изв. АН. Энергетика. 2007. № 5. С. 50.
Азриель В.М., Русин Л.Ю. // Хим. физика. 2008. Т. 27. № 7. С. 5.
Azriel V.M., Kolesnikova E.V., Rusin L.Yu., Sevryuk M.B. // J. Phys. Chem. A. 2011. V. 115. № 25. P. 7055; https://doi.org/10.1021/jp112344j
Kabanov D.B., Rusin L.Yu. // Chem. Phys. 2012. V. 392. № 1. P. 149; https://doi.org/10.1016/j.chemphys.2011.11.009
Кабанов Д.Б., Русин Л.Ю. // Хим. физика. 2012. Т. 31. № 7. С. 16.
Колесникова Е.В., Русин Л.Ю. // Хим. физика. 2012. Т. 31. № 9. С. 3.
Azriel V.M., Rusin L.Yu., Sevryuk M.B. // Chem. Phys. 2013. V. 411. P. 26; https://doi.org/10.1016/j.chemphys.2012.11.016
Ермолова Е.В. Дис. … канд. физ.-мат. наук. М.: ИНЭПХФ РАН им. В.Л. Тальрозе, 2013.
Ермолова Е.В., Русин Л.Ю. // Хим. физика. 2014. Т. 33. № 5. С. 3; https://doi.org/10.7868/S0207401X14050045
Азриель В.М., Колесникова Л.И., Русин Л.Ю. // Хим. физика. 2016. Т. 35. № 8. С. 3; https://doi.org/10.7868/S0207401X16080045
Азриель В.М., Акимов В.М., Ермолова Е.В. и др. // Хим. физика. 2018. Т. 37. № 12. С. 11; https://doi.org/10.1134/S0207401X18120038
Akimov V.M., Azriel V.M., Ermolova E.V. et al. // Phys. Chem. Chem. Phys. 2021. V. 23. № 13. P. 7783; https://doi.org/10.1039/d0cp04183a
Pack R.T., Walker R.B., Kendrick B.K. // J. Chem. Phys. 1998. V. 109. № 16. P. 6701; https://doi.org/10.1063/1.477348
Parker G.A., Walker R.B., Kendrick B.K., Pack R.T. // Ibid. 2002. V. 117. № 13. P. 6083; https://doi.org/10.1063/1.1503313
Ленин Л.В., Русин Л.Ю., Севрюк М.Б. Процессы диссоциации и комплексообразования при столкновениях молекул галогенидов цезия с атомами инертных газов и ртути: импульсная модель. Деп. в ВИНИТИ 10.12.91, № 4561-В91.
Севрюк М.Б. Дис. … д-ра физ.-мат. наук. М.: ИНЭПХФ РАН, 2003.
Русин Л.Ю., Севрюк М.Б. Отчет в ЦИТиС. Рег. номер 215100170008. М.: ИНЭПХФ РАН им. В.Л. Тальрозе, 2015.
Polewczak J., Soares A.J. // Kinetic Related Models. 2017. V. 10. № 2. P. 513; https://doi.org/10.3934/krm.2017020
Carvalho F., Polewczak J., Silva A.W., Soares A.J. // Physica A. 2018. V. 505. P. 1018; https://doi.org/10.1016/j.physa.2018.03.082
Ермолова Е.В., Русин Л.Ю., Севрюк М.Б. // На стыке наук. Физико-химическая серия. III Междунар. науч. интернет-конф. Т. 1. Казань: Индив. предпр. Синяев Д.Н., 2015. С. 111.
Ермолова Е.В., Русин Л.Ю., Севрюк М.Б. // Хим. физика. 2014. Т. 33. № 11. С. 12; https://doi.org/10.7868/S0207401X1411003X
Libby W.F. // J. Amer. Chem. Soc. 1947. V. 69. № 10. P. 2523; https://doi.org/10.1021/ja01202a079
Tully F.P., Cheung N.H., Haberland H., Lee Y.T. // J. Chem. Phys. 1980. V. 73. № 9. P. 4460; https://doi.org/10.1063/1.440683
Зембеков А.А., Маергойз А.И., Никитин Е.Е., Русин Л.Ю. // Теорет. и экспер. хим. 1981. Т. 17. № 5. С. 579.
Зембеков А.А., Маергойз А.И. // Хим. физика. 1984. Т. 3. № 4. С. 495.
Акимов В.М., Маергойз А.И., Русин Л.Ю. // Хим. физика. 1986. Т. 5. № 11. С. 1514.
Lenin L.V., Rusin L.Yu. // Chem. Phys. Lett. 1990. V. 175. № 6. P. 608; https://doi.org/10.1016/0009-2614(90)85589-5
Pérez-Ríos J., Ragole S., Wang J., Greene C.H. // J. Chem. Phys. 2014. V. 140. № 4. P. 044307; https://doi.org/10.1063/1.4861851
Русин Л.Ю., Севрюк М.Б. // Физико-химическая кинетика в газовой динамике. 2016. Т. 17. № 3; http://chemphys.edu.ru/issues/2016-17-3/articles/667/
Luo H., Alexeenko A.A., Macheret S.O. // J. Thermophys. Heat Transfer. 2018. V. 32. № 4. P. 861; https://doi.org/10.2514/1.T5375
Luo H., Sebastião I.B., Alexeenko A.A., Macheret S.O. // Phys. Rev. Fluids. 2018. V. 3. № 11. P. 113401; https://doi.org/10.1103/PhysRevFluids.3.113401
Luo H., Alexeenko A.A., Macheret S.O. // Phys. Fluids. 2019. V. 31. № 8. P. 087105; https://doi.org/10.1063/1.5110162
Jepsen D.W., Hirschfelder J.O. // J. Chem. Phys. 1959. V. 30. № 4. P. 1032; https://doi.org/10.1063/1.1730079
Akimov V.M., Lenin L.V., Rusin L.Yu. // Chem. Phys. Lett. 1991. V. 180. № 6. P. 541; https://doi.org/10.1016/0009-2614(91)85006-I
Русин Л.Ю., Севрюк М.Б. // Хим. физика. 1993. Т. 12. № 6. С. 839.
Левантовский В.И. Механика космического полета в элементарном изложении. М.: Наука, 1980.
Curtis H.D. Orbital Mechanics for Engineering Students. Amsterdam: Elsevier Butterworth-Heinemann, 2005.
Суханов А.А. Астродинамика. М.: Изд-во ИКИ РАН, 2010.
Brumer P. // Phys. Rev. A. 1974. V. 10. № 1. P. 1; https://doi.org/10.1103/PhysRevA.10.1
Кнунянц И.Л. (гл. ред.). Химическая энциклопедия. Т. 1. М.: Советская энциклопедия, 1988.
Кнунянц И.Л. (гл. ред.). Химическая энциклопедия. Т. 2. М.: Советская энциклопедия, 1990.
Зефиров Н.С. (гл. ред.). Химическая энциклопедия. Т. 4. М.: Большая Российская энциклопедия, 1995.
Радциг А.А., Смирнов Б.М. Справочник по атомной и молекулярной физике. М.: Атомиздат, 1980.
Радциг А.А., Смирнов Б.М. Параметры атомов и атомных ионов. М.: Энергоатомиздат, 1986.
Patil S.H. // J. Chem. Phys. 1987. V. 86. № 12. P. 7000; https://doi.org/10.1063/1.452348
Patil S.H. // Ibid. 1988. V. 89. № 10. P. 6357; https://doi.org/10.1063/1.455403
Koutselos A.D., Mason E.A., Viehland L.A. // Ibid. 1990. V. 93. № 10. P. 7125; https://doi.org/10.1063/1.459436
Gilbert T.L., Simpson O.C., Williamson M.A. // Ibid. 1975. V. 63. № 9. P. 4061; https://doi.org/10.1063/1.431848
Gatland I.R., Thackston M.G., Pope W.M. et al. // Ibid. 1978. V. 68. № 6. P. 2775; https://doi.org/10.1063/1.436069
Inouye H., Noda K., Kita S. // Ibid. 1979. V. 71. № 5. P. 2135; https://doi.org/10.1063/1.438586
Viehland L.A. // Chem. Phys. 1984. V. 85. № 2. P. 291; https://doi.org/10.1016/0301-0104(84)85040-5
Grycuk T., Findeisen M. // J. Phys. B. 1983. V. 16. № 6. P. 975; https://doi.org/10.1088/0022-3700/16/6/014
Русин Л.Ю., Севрюк М.Б. Отчет в ЦИТиС. Рег. номер АААА-Б16-216092340017-7. М.: ИНЭПХФ РАН им. В.Л. Тальрозе, 2016.
Русин Л.Ю., Севрюк М.Б., Азриель В.М., Акимов В.М., Кабанов Д.Б. Отчет в ЦИТиС. Рег. номер 216032240003. М.: ИНЭПХФ РАН им. В.Л. Тальрозе, 2016.
Савельев И.В. Курс общей физики. Т. 2. Электричество и магнетизм, волны, оптика. М.: Наука, 1982.
Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. М.: ИНФРА‑М, 2002.
Елисеева И.И., Егорова И.И., Курышева С.В. и др. Статистика. М.: Проспект, 2010.
Голубков Г.В., Бычков В.Л., Арделян Н.В., Космачевский К.В., Голубков М.Г. // Хим. физика. 2019. Т. 38. № 7. С. 23; https://doi.org/10.1134/S0207401X19070045
Голубков Г.В., Бычков В.Л., Готовцев В.О. и др. // Хим. физика. 2020. Т. 39. № 4. С. 51; https://doi.org/10.31857/S0207401X2004007X
Голубков Г.В., Маслов Т.А., Бычков В.Л. и др. // Хим. физика. 2020. Т. 39. № 10. С. 47; https://doi.org/10.31857/S0207401X20100052
Левин П.П., Ефремкин А.Ф., Худяков И.В. // Хим. физика. 2020. Т. 39. № 6. С. 59; https://doi.org/10.31857/S0207401X20060059
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика