Химическая физика, 2021, T. 40, № 2, стр. 29-32

ВВЕДЕНИЕ

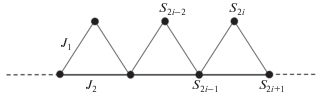
Низкоразмерные квантовые магнетики на геометрически фрустрированных решетках вызывают значительный интерес как с экспериментальной, так и с теоретической точек зрения [1–3]. Важным классом таких объектов являются соединения, состоящие из треугольных кластеров магнитных ионов. К ним, например, относятся магнетики на двумерных и квазиодномерных решетках кагоме, решетках пирохлора и ряде других. Простейшим и типичным примером такой системы является так называемая дельта-цепочка, представляющая собой линейную цепь треугольников с магнитными ионами со спином 1/2 в их узлах (рис. 1 ). Магнитные свойства такой системы описываются моделью Гейзенберга, имеющей вид

Рис. 1.

Спиновая модель дельта-цепочки.

Квантовая дельта-цепочка, со спином s = 1/2 с обоими антиферромагнитными (AF) взаимодействиями: J₁ > 0, J₂ > 0, достаточно хорошо изучена и обладает рядом интересных свойств [2, 4–7]. В частности, при J₂ = J₁/2 и магнитном поле, близком к насыщению, кривая намагниченности имеет плато со скачком намагниченности, а теплоемкость наряду с широким высокотемпературным максимумом имеет дополнительный низкотемпературный пик.

В то же время дельта-цепочка с s = 1/2, ферромагнитным взаимодействием J₁ и антиферромагнитным взаимодействием J₂ (J₁ < 0, J₂ > 0) (F–AF-модель) также весьма интересна, но до недавнего времени была изучена существенно меньше. Особый интерес вызывает изучение ее магнитных свойств в зависимости от значения параметра фрустрации α = J₂/|J₁|. Ранее было лишь известно, что основное состояние F–AF-цепочки ферромагнитно, если параметр фрустрации α < 1/2, но структура основного состояния при α > 1/2 до конца оставалась невыясненной, хотя и предполагалось, что основное состояние магнитоупорядоченно (ферримагнитно) при α > 1/2. Критическое значение параметра фрустрации α_сr = = 1/2 разделяет эти две фазы.

Дополнительной мотивацией для изучения F–AF-дельта-цепочки стало появление реальных соединений, описываемых этой моделью. Примером такого рода соединений являются комплексы [CuH₂O] ⋅ [Cu(mal)H₂O](ClO₄)₂, содержащие магнитные ионы Cu²⁺ со спином 1/2 [8, 9]. Из анализа экспериментальных данных было установлено, что параметр фрустрации α в этом соединении примерно равен единице.

Другим очень интересным примером соединений, описываемых F–AF-моделью, являются недавно синтезированные циклические комплексы, содержащие магнитные молекулы Fe₁₀Gd₁₀ с рекордным значением спина основного состояния молекулы: S = 60 [10]. Оценка значения параметра фрустрации для этой молекулы показывает, что α = 0.46 [10]. Имеются также и другие примеры ферримагнитных молекулярных магнетиков [11].

Как было отмечено выше, при α < 1/2 основное состояние s = 1/2 F–AF-цепочки является ферромагнитным, т.е. спин основного состояния S = N/2 (N – число спинов цепочки). Значение параметра фрустрации α_cr = 1/2 соответствует квантовой критической точке; F–AF-модель при α = α_сr была детально исследована в наших работах [12–14]. В частности, подробный анализ этой весьма нетривиальной модели был недавно приведен в работе [15]. Напомним кратко об основных особенностях F–AF-цепочки при α = α_сr. Точными основными состояниями модели (1) являются как локализованные многомагнонные состояния, так и связанные состояния магнонов специального класса. Основное состояние реализуется при любом значении полного спина, и число всех основных состояний экспоненциально велико. Вследствие этого энтропия, приходящаяся на один спин, при нулевой температуре конечна и равна ln(2)/2. Спектр возбуждений имеет экспоненциально малую щель, что приводит к необычному поведению низкотемпературной термодинамики. Эти свойства модели представляют несомненный интерес. Однако едва ли можно ожидать, что в настоящее время возможен синтез соединений, описываемых F–AF-моделью с параметром фрустрации, в точности равным критическому. (Заметим, тем не менее, что в магнитной молекуле Fe₁₀Gd₁₀ параметр фрустрации близок к критическому значению.) Поэтому возникает вопрос о свойствах модели при произвольных значениях параметра α. Свойства модели в ферромагнитной фазе при α < 1/2 исследованы достаточно подробно. В частности, было изучено низкотемпературное поведение модели в этой фазе [14, 15], и был проведен анализ экспериментально наблюдаемых свойств магнитной молекулы Fe₁₀Gd₁₀, параметр фрустрации которой α < 1/2.

В настоящей работе мы остановимся на изучении F–AF-дельта-цепочки при α > 1/2. Как мы отмечали выше, вопрос о природе основного состояния в этой фазе остается открытым, хотя есть определенные основания ожидать, что основное состояние при α > 1/2 ферримагнитно, т.е. величина магнитного момента, приходящегося на один узел, отлична от нуля, но меньше максимального значения, равного 1/2. Например, в нашей работе [13] по изучению F–AF-дельта-цепочки в случае предельной величины анизотропии обменных взаимодействий показано, что фазовая диаграмма основного состояния состоит из ферромагнитной и ферримагнитной фаз с критической линией между ними, и такая картина может также сохраниться и для изотропной модели (1). Тем не менее, этот вопрос требует дополнительного исследования.

ФЕРРИМАГНИТНАЯ ФАЗА

Для начала интересно рассмотреть этот вопрос для классической версии модели (1). В классическом приближении операторы спина s = 1/2 заменяются векторами с длиной s: S_i = sn_i (n_i – единичный вектор), и квантовый гамильтониан (1) сводится к классическому. Для дальнейшего рассмотрения удобно представить этот гамильтониан в виде суммы гамильтонианов отдельных треугольников:

где H_i – гамильтониан i-того треугольника, имеющий вид (с заменой S на n)

где мы приняли, что J₁ = –1, а J₂ = α.

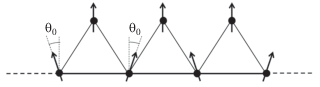
Легко убедиться, что для α ≤ 1/2 основное состояние гамильтониана (2) является тривиальным ферромагнитным с параллельной ориентацией всех спинов. При α > 1/2 минимальная энергия (3) отдельного треугольника соответствует ферримагнитной конфигурации, показанной на рис. 2 , в которой все спины треугольника, n₁, n₂, n₃, лежат в одной плоскости и угол между спинами n₁, n₃ и вершинным спином n₂ равен θ₀, где

Рис. 2.

Ферримагнитное состояние классической дельта-цепочки.

Согласно (4), магнитный момент m каждого треугольника равен

и параллелен спину n₂.

На первый взгляд кажется, что полный магнитный момент цепочки равен nm, где n – число треугольников. Этот результат был бы справедлив, если бы все треугольники цепочки лежали в одной плоскости и все вершинные спины были бы параллельны. В действительности, конфигурация основного состояния необязательно должна быть компланарной. Рассмотрим, например, два соседних треугольника со спинами (n₁, n₂, n₃) и (n₃, n₄, n₅). Спины треугольника (n₁, n₂, n₃) лежат в одной плоскости, и их конфигурация удовлетворяет условию (4). Спины соседнего треугольника (n₃, n₄, n₅) также образуют ферримагнитную конфигурацию, но они могут лежать в любой плоскости, полученной в результате вращения этого треугольника вокруг спина n₃ на произвольный угол, так что основное состояние второго треугольника вырождено по углу между плоскостями (n₁, n₂, n₃) и (n₃, n₄, n₅). Затем плоскость третьего треугольника – (n₅, n₆, n₇) может быть повернута на произвольный угол вокруг спина n₅ и т.д. В результате основное состояние классической дельта-цепочки при α > 1/2 бесконечно вырождено. Все конфигурации основного состояния могут быть описаны как случайные блуждания конечной длины на поверхности сферы. Усреднение по всем конфигурациям основного состояния приводит к нулевой намагниченности, несмотря на конечную намагниченность каждого треугольника. Магнитный момент в слабом магнитном поле (h $ \ll $ T) растет линейно с увеличением напряженности поля [14]:

В отличие от классической модели, которая допускает аналитическое рассмотрение, квантовая F–AF-дельта-цепочка при α > 1/2 может быть изучена лишь на основе приближенных методов или численных расчетов конечных цепочек. В проведенных нами численных расчетах спина основного состояния мы использовали как точную диагонализацию (exact diagonalization (ED)) соответствующих матриц, так и высокоэффективные приближенные методы, основанные на ренормгрупповой процедуре (DMRG), позволяющие существенно увеличить размеры цепочки по сравнению с доступными для ED-вычислений.

Оказалось, однако, что результаты расчетов основного состояния зависят от граничных условий (т.е. от того, являются ли цепочки циклическими или открытыми) и от четности числа треугольников в цепочке. Например, спин основного состояния S_tot циклической цепочки с четным числом треугольников уменьшается постепенно или скачками от S_tot = (N/4 + 1) до S_tot = 0 при увеличении α от 1/2 до величины α₀, зависящей от N. Согласно численным расчетам, α₀ ~ 1, ~2, ~3 для N = 20, 24 и 36 соответственно. Такая же ситуация наблюдается и для открытых цепочек с нечетным числом треугольников. С другой стороны, для открытых цепочек с четным числом треугольников спин S_tot был равен (N + 1)/4 при всех значениях параметра α > 1/2 и для рассчитанных нами цепочек (до N ~ 60). (Заметим, что подобное различие в поведении спина основного состояния было обнаружено ранее в работе [16].) Как будет обсуждено ниже, это различие в поведении S_tot обусловлено эффектом конечномерности, и при N $ \gg $ 1 полный спин S_tot не должен зависеть от типа цепочки. Для решения этого вопроса полезно рассмотреть дельта-цепочку при больших значениях параметра фрустрации. В пределе α = ∞ модель распадается на две несвязанные подсистемы: антиферромагнитную цепочку и подсистему невзаимодействующих спинов на вершинах треугольников. При больших, но конечных значениях α взаимодействие между подсистемами можно учесть в рамках теории возмущений по величине 1/α. В этом случае удобно принять J₂ = 1, J₁ = –1/α, и гамильтониан (1) будет иметь вид

где H₀ – гамильтониан антиферромагнитной цепочки спинов основания, а V – их взаимодействие со спинами вершин. Пусть циклическая цепочка содержит n треугольников и n спинов основания (n = N/2) и n четно. Тогда основное состояние H₀ является синглетом, и в силу его симметрии поправка первого порядка равна нулю. При этом вершинная подсистема вырождена по спину. Однако для триплета с S_tot = 1 поправка первого порядка отлична от нуля. Она равна среднему 〈V〉 по триплету, которое имеет вид

Среднее $\left\langle {S_{{2i}}^{z} + S_{{2i + 1}}^{z}} \right\rangle $ по триплетному состоянию равно 2/n, и минимум (9) достигается при $S_{{2i}}^{z} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ т.е. подсистема вершинных спинов находится в ферромагнитном состоянии и S_tot = (n/2 + 1). (Заметим, что именно такое значение S_tot имеют циклические цепочки с n ~ 10 при α ~ 1.) При этом $\left\langle V \right\rangle = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} \alpha }} \right. \kern-0em} \alpha }.$ Разность энергий ΔE нижайшего триплета и синглета AF-цепочки Гейзенберга, как известно, равна ΔE = π²/n, и переход из состояния с S_tot = 0 в состояние с S_tot = (n/2 + 1) при большом значении α происходит при n > π²α. Для α = 10 соответствующее n ~ 100 (N ~ 200), но численные расчеты таких больших цепочек пока нельзя провести. Что касается открытых дельта-цепочек с четным числом треугольников, то AF-подсистема имеет нечетное число спинов, ее основное состояние имеет спин 1/2 и вклад первого порядка отличен от нуля. Подсистема вершинных спинов находится в ферромагнитном состоянии, и S_tot = = n/2 + 1/2, как и наблюдается в численных расчетах таких цепочек. Таким образом, при больших значениях α спин основного состояния открытых и достаточно больших циклических цепочек равен N/4. Необходимо, однако, отметить, что выше мы рассматривали вклады первого порядка по V для состояний антиферромагнитной цепочки с S = 1 и S = 1/2 для циклической и открытой цепочек соответственно. Это правильно, когда число спинов составляет сотни или тысячи. Если, однако, цепочка имеет макроскопические размеры, стартовым является состояние с также макроскопическим спином S AF-цепочки. В этом случае $\left\langle V \right\rangle $ = –S/α и полная энергия равна

где E  (S) – энергия нижайшего состояния со спином S AF-цепочки Гейзенберга, которая при S $ \ll $ n равна [17]

Здесь E₀ – энергия основного состояния AF-цепочки.

Минимизация (10) по S дает оптимальное значение спина AF-подсистемы:

и полный спин S_tot равен

Таким образом, при больших значениях α спин основного состояния составляет половину от максимального значения, равного N/2. При этом магнитные моменты, приходящиеся на один узел антиферромагнитной цепочки и вершинной подсистемы, равны 1/π²α и 1/2 соответственно. Хотя полученный результат относится к области больших значений α, можно ожидать, что спин основного состояния S_tot будет описываться формулой (13) при всех α > 1/2, и это имеет место как для открытых цепочек с четным числом треугольников, так и для достаточно больших циклических цепочек.

ЗАКЛЮЧЕНИЕ

Мы изучили модель дельта-цепочки с ферро- и антиферромагнитными обменными взаимодействиями. Основное внимание уделено области значений параметра фрустрации α > 1/2. Показано, что некоторые противоречия в результатах численных расчетов обусловлены эффектом конечности рассчитываемых цепочек. На основании анализа модели при больших значениях α сделан вывод о том, что основное состояние при α > 1/2 ферримагнитно и его полный спин S_tot зависит от α и превышает N/4. Недавние численные расчеты, проведенные в работе [18], подтверждают этот вывод. Таким образом, основное состояние квантовой F–AF-модели при α > 1/2 является магнитоупорядоченным в отличие от классической модели, где оно бесконечно вырождено и разупорядоченно. Таким образом, рассматриваемая модель принадлежит к классу систем, в которых реализуется явление “порядок из беспорядка” (“order by disorder”), когда квантовые флуктуации формируют упорядоченное состояние из разупорядоченного.