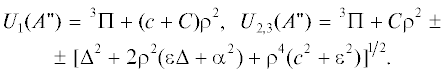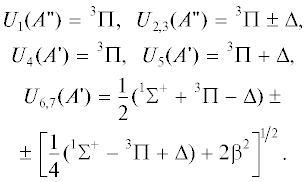1. На главную
  2. Электронные версии
  3. Химическая физика
  4. T. 40, № 3, 2021

Химическая физика, 2021, T. 40, № 3, стр. 3-9

Синглет-триплетное взаимодействие состояний 3Π и 1Σ+ в линейных трехатомных молекулах

В. М. Волохов 1, *, Л. В. Полуянов 1

1 Институт проблем химической физики Российской академии наук
Черноголовка, Россия

* E-mail: vvm@icp.ac.ru

Поступила в редакцию 19.11.2019
После доработки 23.12.2019
Принята к публикации 20.01.2020

Полный текст (PDF)

Аннотация

В работе предложена двухэлектронная модель, описывающая синглет-триплетное взаимодействие состояний 1Σ+ и 3Π в линейных трехатомных молекулах. Анализ основан на учете спин-орбитального взаимодействия в электронном гамильтониане, а также на использовании его свойств симметрии. Показано, что операторы симметрии электронного гамильтониана содержат как пространственные (действующие на координаты электронов), так и матричные операции (действующие на электронные спины). В работе учитываются только деформационные π-моды, и полученная вибронная матрица 7 × 7 фактически описывает релятивистский псевдо-эффект Реннера (3Π + 1Σ+) × π. Собственные значения вибронной матрицы (т.е. поверхности потенциальной энергии) являются аксиально-симметричными. Вибронная матрица содержит девять параметров. Три из них имеют электростатическое происхождение, а шесть параметров обусловлены спин-орбитальным взаимодействием.

Ключевые слова: спин-орбитальное взаимодействие, релятивистский эффект псевдо-Реннера, группа симметрии, пространственно-матричные операторы симметрии, электронный гамильтониан, электронный базис спин-орбиталей, вибронная матрица, вибронные операторы симметрии.

ВВЕДЕНИЕ

В нерелятивистской теории потенциальные поверхности электронных состояний 3Π и 1Σ+ линейной трехатомной молекулы имеют различную пространственную симметрию и мультиплетность и могут пересекаться вдоль одной или нескольких кривых [1]. При учете спин-орбитального взаимодействия молекулярный спин и проекция орбитального углового момента на молекулярную ось не сохраняются, и упомянутые электронные состояния начинают взаимодействовать. В результате возможное пересечение нерелятивистских термов 3Π и 1Σ+ заменяется более сложной его конфигурацией.

В данной работе предложена двухэлектронная модель взаимодействия термов 3Π и 1Σ+ с учетом только деформационных π-мод и спин-орбитального взаимодействия в электронном гамильтониане [2]. Поскольку функциональный вид результирующей вибронной матрицы определяется только свойствами симметрии системы и соответствующими квантовыми числами [3], то двухэлектронная модель взаимодействия термов 3Π и 1Σ+ может быть применена и к многоэлектронным линейным трехатомным молекулам с четным числом электронов и тремя различными атомами. От числа электронов будут зависеть только значения постоянных параметров вибронной матрицы [4].

Взаимодействие термов 3Π и 1Σ+ проявляется наиболее существенно, когда в молекулярном спектре электронные состояния 3Π и 1Σ+ являются соседними и разделены сравнительно небольшим энергетическим интервалом. В этом случае взаимодействие 3Π и 1Σ+ фактически представляет собой релятивистский псевдо-эффект Реннера типа (3Π + 1Σ+) × π.

Полученная в работе вибронная матрица может быть применена к изучению интеркомбинационных переходов типа 3Π ← 1Σ+ в линейных трехатомных молекулах.

СИММЕТРИЯ ДВУХЭЛЕКТРОННОГО ГАМИЛЬТОНИАНА

Основным релятивистским эффектом в реннеровских системах является спин-орбитальное взаимодействие. С учетом последнего электронный гамильтониан представим в виде суммы двух операторов – электростатического гамильтониана ${{\hat {H}}_{{es}}}$ и спин-орбитального взаимодействия ${{\hat {H}}_{{so}}}{\text{:}}$

(1)
$\hat {H} = {{\hat {H}}_{{es}}} + {{\hat {H}}_{{so}}}.$

Мы не приводим здесь конкретный вид операторов ${{\hat {H}}_{{es}}}$ и ${{\hat {H}}_{{so}}},$ которые представлены во многих публикациях и хорошо известны [3–6].

Если молекула имеет линейную форму, то электронный гамильтониан (1) характеризуется точечной группой симметрии ${{C}_{{\infty {v}}}}.$ Операторы этой группы, коммутирующие с гамильтонианом $\hat {H},$ имеют вид

(2)
$\hat {G}_{z}^{{\varepsilon }} = {{\hat {C}}_{1}}(\varepsilon ){{\hat {C}}_{2}}(\varepsilon ){{\left( {\begin{array}{*{20}{c}} {{{e}^{{{{i{\varepsilon }} \mathord{\left/ {\vphantom {{i{\varepsilon }} 2}} \right. \kern-0em} 2}}}}}&0 \\ 0&{{{e}^{{{{ - i{\varepsilon }} \mathord{\left/ {\vphantom {{ - i{\varepsilon }} 2}} \right. \kern-0em} 2}}}}} \end{array}} \right)}_{1}}{{\left( {\begin{array}{*{20}{c}} {{{e}^{{{{i{\varepsilon }} \mathord{\left/ {\vphantom {{i{\varepsilon }} 2}} \right. \kern-0em} 2}}}}}&0 \\ 0&{{{e}^{{{{ - i{\varepsilon }} \mathord{\left/ {\vphantom {{ - i{\varepsilon }} 2}} \right. \kern-0em} 2}}}}} \end{array}} \right)}_{2}}$

единичный оператор,

(3)
${{\hat {Z}}_{{\sigma }}} = \hat {\sigma }_{{xz}}^{{(1)}}\hat {\sigma }_{{xz}}^{{(2)}}{{\left( {\begin{array}{*{20}{c}} 0&1 \\ { - 1}&0 \end{array}} \right)}_{1}}{{\left( {\begin{array}{*{20}{c}} 0&1 \\ { - 1}&0 \end{array}} \right)}_{2}}.$

В формулах (2), (3) индексы “1” и “2” указывают, на какой электрон в электронном гамильтониане действует данный оператор. Пространственно-матричные двухэлектронные операторы $\hat {G}_{z}^{{\varepsilon }}$ и ${{\hat {Z}}_{{\sigma }}}$ соответствуют повороту на угол ε вокруг молекулярной оси $z\left( {\hat {G}_{z}^{{\varepsilon }}} \right)$ и отражению в вертикальной плоскости $xz({{\hat {Z}}_{{\sigma }}}).$ Они действуют как на координаты электронов, так и на операторы электронных спинов (матрицы Паули) в электронном гамильтониане $\hat {H}.$

Помимо этих пространственно-матричных операторов симметрии, электронный гамильтониан $\hat {H}$ характеризуется еще одним оператором симметрии – оператором обращения времени [7, 8]; в частности, $\hat {H}$ коммутирует с оператором $\hat {T}{\text{:}}$

(4)
$\hat {T} = {{\left( {\begin{array}{*{20}{c}} 0&{ - i} \\ i&0 \end{array}} \right)}_{1}}{{\left( {\begin{array}{*{20}{c}} 0&{ - i} \\ i&0 \end{array}} \right)}_{2}}\widehat {{\text{c}}{\text{.c}}{\text{.}}},$

где $\widehat {{\text{c}}{\text{.c}}{\text{.}}}$ – оператор комплексного сопряжения. Отметим, что оператор обращения времени $\hat {T}$ является антиунитарным [8]. Для рассматриваемой модели с четным числом электронов имеет место равенство ${{\hat {T}}^{2}} = + 1$.

РАЗЛОЖЕНИЕ ЭЛЕКТРОННОГО ГАМИЛЬТОНИАНА В РЯД ТЕЙЛОРА

Разложение электронного гамильтониана в ряд Тейлора по π-модам удобно вести в терминах величин, принадлежащих неприводимым представлениям группы молекулярной симметрии ${{C}_{{\infty {v}}}}.$ В табл. 1 мы приводим соответствующие симметризованные комбинации вплоть до вкладов второго порядка по π-модам. Разложение электростатического гамильтониана в ряд Тейлора имеет вид

(5)
${{\hat {H}}_{{es}}} = {{\hat {H}}_{0}} + {{\hat {H}}_{1}} + {{\hat {H}}_{2}} + ...,$
Таблица 1.  

Симметризованные комбинации нормальных мод и матриц Паули

Степени нормальных мод Номера симметризованных комбинаций Симметрия Тип нормальной моды и матриц Паули Симметризованные комбинации
1-й орбитальный 1 π q ${{q}_{ + }} = {{q}_{x}} + i{{q}_{y}},$${{q}_{ - }} = {{q}_{x}} - i{{q}_{y}}$
2-й орбитальный 2 σ+ qq  ${{q}_{ + }}{{q}_{ - }}$
3 δ qq $q_{ + }^{2},$$q_{ - }^{2}$
0-й спин-орбитальный 4, 5 σ– σ $\hat {\sigma }_{z}^{{(1)}},$$\hat {\sigma }_{z}^{{(2)}}$
6 π σ $\hat {\sigma }_{ + }^{{(1)}} = {{\left( {\hat {\sigma }_{y}^{{(1)}} - i\hat {\sigma }_{x}^{{(1)}}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {\sigma }_{y}^{{(1)}} - i\hat {\sigma }_{x}^{{(1)}}} \right)} 2}} \right. \kern-0em} 2},$$\hat {\sigma }_{ - }^{{(1)}} = {{\left( {\hat {\sigma }_{y}^{{(1)}} + i\hat {\sigma }_{x}^{{(1)}}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {\sigma }_{y}^{{(1)}} + i\hat {\sigma }_{x}^{{(1)}}} \right)} 2}} \right. \kern-0em} 2}$
7 $\hat {\sigma }_{ + }^{{(2)}} = {{\left( {\hat {\sigma }_{y}^{{(2)}} - i\hat {\sigma }_{x}^{{(2)}}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {\sigma }_{y}^{{(2)}} - i\hat {\sigma }_{x}^{{(2)}}} \right)} 2}} \right. \kern-0em} 2},$$\hat {\sigma }_{ - }^{{(2)}} = {{\left( {\hat {\sigma }_{y}^{{(2)}} + i\hat {\sigma }_{x}^{{(2)}}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {\sigma }_{y}^{{(2)}} + i\hat {\sigma }_{x}^{{(2)}}} \right)} 2}} \right. \kern-0em} 2}$
1-й спин-орбитальный 8, 9 k = 1, 2 σ+ qσ ${{q}_{ - }}\hat {\sigma }_{ + }^{{(k)}} + {{q}_{ + }}\hat {\sigma }_{ - }^{{(k)}}$
10, 11 k = 1, 2 σ– qσ ${{q}_{ - }}\hat {\sigma }_{ + }^{{(k)}} - {{q}_{ + }}\hat {\sigma }_{ - }^{{(k)}}$
12, 13 k = 1, 2 π qσ ${{q}_{ + }}\hat {\sigma }_{z}^{{(k)}},$$ - {{q}_{ - }}\hat {\sigma }_{z}^{{(k)}}$
14, 15 k = 1, 2 δ qσ ${{q}_{ + }}\hat {\sigma }_{ + }^{{(k)}},$${{q}_{ - }}\hat {\sigma }_{ - }^{{(k)}}$
2-й спин-орбитальный 16, 17 k = 1, 2 σ– q2σ ${{q}_{ + }}{{q}_{ - }}\hat {\sigma }_{z}^{{(k)}}$
18, 19 k = 1, 2 π q2σ ${{q}_{ + }}{{q}_{ - }}\hat {\sigma }_{ + }^{{(k)}},$${{q}_{ + }}{{q}_{ - }}\hat {\sigma }_{ - }^{{(k)}}$
20, 21 k = 1, 2 π q2σ $q_{ + }^{2}\hat {\sigma }_{ - }^{{(k)}},$$q_{ - }^{2}\hat {\sigma }_{ + }^{{(k)}}$
22, 23 k = 1, 2 δ q2σ $q_{ + }^{2}\hat {\sigma }_{z}^{{(k)}},$$ - q_{ - }^{2}\hat {\sigma }_{z}^{{(k)}}$
24, 25 k = 1, 2 Φ q2σ $q_{ + }^{2}\hat {\sigma }_{ + }^{{(k)}},$$q_{ - }^{2}\hat {\sigma }_{ - }^{{(k)}}$

где ${{\hat {H}}_{0}}$ – нерелятивистский (электростатический) гамильтониан линейной молекулы,

(6)
${{\hat {H}}_{1}} = {{\hat {H}}_{ + }}({{\pi }_{ - }}){{q}_{ + }} + {{\hat {H}}_{ - }}({{\pi }_{ + }}){{q}_{ - }},$
(7)
${{\hat {H}}_{2}} = {{\hat {H}}_{{ + + }}}({{\delta }_{ - }})q_{ + }^{2} + {{\hat {H}}_{{ - - }}}({{\delta }_{ + }})q_{ - }^{2} + {{\hat {H}}_{{ + - }}}({{\sigma }^{ + }}){{q}_{ + }}{{q}_{ - }}.$

В терминах симметризованных комбинаций из табл. 1 ряд Тейлора для спин-орбитального взаимодействия выглядит следующим образом:

(8)
${{\hat {H}}_{{so}}} = {{\hat {h}}_{0}} + {{\hat {h}}_{1}} + {{\hat {h}}_{2}} + ...,$

где

(9)
${{\hat {h}}_{0}} = \sum\limits_{k = 1,2} {\left[ {{}^{k}{{{\hat {h}}}_{ + }}({{\pi }_{ - }})\hat {\sigma }_{ + }^{{(k)}} + {}^{k}{{{\hat {h}}}_{ - }}({{\pi }_{ + }})\hat {\sigma }_{ - }^{{(k)}} + {}^{k}{{{\hat {h}}}_{z}}({{\sigma }^{ - }})\hat {\sigma }_{z}^{{(k)}}} \right]} ,$
(10)
$\begin{gathered} {{{\hat {h}}}_{1}} = \sum\limits_{k = 1,2} {\left[ {{}^{k}\hat {h}_{ + }^{ + }\left( {{{\delta }_{ - }}} \right){{q}_{ + }}\hat {\sigma }_{ + }^{{(k)}} + {}^{k}\hat {h}_{ - }^{ - }\left( {{{\delta }_{ + }}} \right){{q}_{ - }}\hat {\sigma }_{ - }^{{(k)}} + } \right.} \\ + \,\,{}^{k}{{{\hat {h}}}^{ + }}\left( {{{\sigma }^{ + }}} \right)\left( {{{q}_{ - }}\hat {\sigma }_{ + }^{{(k)}} + {{q}_{ + }}\hat {\sigma }_{ - }^{{(k)}}} \right) + {}^{k}{{{\hat {h}}}^{ - }}\left( {{{\sigma }^{ - }}} \right) \times \\ \times \,\,\left( {{{q}_{ - }}\hat {\sigma }_{ + }^{{(k)}} - {{q}_{ + }}\hat {\sigma }_{ - }^{{(k)}}} \right) + {}^{k}\hat {h}_{z}^{ + }\left( {{{\pi }_{ - }}} \right){{q}_{ + }}\hat {\sigma }_{z}^{{(k)}} - \\ \left. { - \,\,{}^{k}\hat {h}_{z}^{ - }\left( {{{\pi }_{ + }}} \right){{q}_{ - }}\hat {\sigma }_{z}^{{(k)}}} \right], \\ \end{gathered} $
(11)
$\begin{gathered} {{{\hat {h}}}_{2}} = \sum\limits_{k = 1,2} {\left\{ {\left[ {{}^{k}\hat {h}_{ + }^{{ + + }}({{\Phi }_{ - }})q_{ + }^{2} + {}^{k}\hat {h}_{ + }^{{ - - }}\left( {{{\pi }_{ + }}} \right)q_{ - }^{2} + } \right.} \right.} \\ \left. { + \,\,{}^{k}\hat {h}_{ + }^{{ + - }}\left( {{{\pi }_{ - }}} \right){{q}_{ + }}{{q}_{ - }}} \right]\hat {\sigma }_{ + }^{{(k)}} + \left[ {{}^{k}\hat {h}_{ - }^{{ + + }}\left( {{{\pi }_{ - }}} \right)q_{ + }^{2} + } \right. \\ \left. { + \,\,{}^{k}\hat {h}_{ - }^{{ - - }}({{\Phi }_{ + }})q_{ - }^{2} + {}^{k}\hat {h}_{ - }^{{ + - }}\left( {{{\pi }_{ + }}} \right){{q}_{ + }}{{q}_{ - }}} \right]\hat {\sigma }_{ - }^{{(k)}} + \\ \left. { + \left[ {{}^{k}\hat {h}_{z}^{{ + + }}({{\delta }_{ - }})q_{ + }^{2} - {}^{k}\hat {h}_{z}^{{ - - }}({{\delta }_{ + }})q_{ - }^{2} + {}^{k}\hat {h}_{z}^{{ + - }}\left( {{{\sigma }^{ - }}} \right){{q}_{ + }}{{q}_{ - }}} \right]\hat {\sigma }_{z}^{{(k)}}} \right\} \\ \end{gathered} $

Каждый операторный коэффициент рядов Тейлора (5)–(11) преобразуется по неприводимому представлению и его строчке, указанных в качестве аргумента этого оператора. Подчеркнем, что все операторные коэффициенты рядов Тейлора (5)–(11) преобразуются по неприводимым представлениям, которые комплексно сопряжены неприводимым представлениям соответствующих симметризованных комбинаций. В соответствии с изложенным в §102 из работы [7] данная симметрия операторных коэффициентов обеспечивает необходимую инвариантность в симметрии ${{C}_{{\infty {v}}}}$ операторов ${{\hat {H}}_{i}}\,(i = 1,2)$ и ${{\hat {h}}_{j}}\,(j = 0,1,2).$

ДИАБАТИЧЕСКИЙ БАЗИС ЭЛЕКТРОННЫХ СОСТОЯНИЙ

Ниже будем использовать цилиндрические координаты, в которых ось z совпадает с осью симметрии линейной молекулы, r – цилиндрический радиус и ϕ – угол поворота вокруг оси z. Введем одну электронную молекулярную орбиталь, Q(r, z), с симметрией Σ+ и две молекулярные Π‑орбитали, $P(r,z)\exp ( \pm i\varphi ).$

Диабатический базис двухэлектронных спин-орбиталей ${{\psi }_{{{{J}_{z}}}}}({{L}_{z}},{{S}_{z}})$ записываем в порядке уменьшения квантового числа проекции полного углового момента ${{J}_{z}} = {{L}_{z}} + {{S}_{z}}{\text{:}}$

(12)
$\left\{ \begin{gathered} {{\psi }_{2}}(1,1) = \frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left[ {Q(2)P(1){{e}^{{i{{{\varphi }}_{1}}}}} - Q(1)P(2){{e}^{{i{{{\varphi }}_{2}}}}}} \right]{{\alpha }_{1}}{{\alpha }_{2}}, \hfill \\ {{\psi }_{1}}(1,0) = \frac{1}{2}\left[ {Q(2)P(1){{e}^{{i{{{\varphi }}_{1}}}}} - Q(1)P(2){{e}^{{i{{{\varphi }}_{2}}}}}} \right]\left( {{{\alpha }_{1}}{{\beta }_{2}} + {{\alpha }_{2}}{{\beta }_{1}}} \right), \hfill \\ {{\psi }_{0}}(1, - 1) = \frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left[ {Q(2)P(1){{e}^{{i{{{\varphi }}_{1}}}}} - Q(1)P(2){{e}^{{i{{{\varphi }}_{2}}}}}} \right]{{\beta }_{1}}{{\beta }_{2}}, \hfill \\ {{{\bar {\psi }}}_{0}}(0,0) = \frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}Q(1)Q(2)\left( {{{\alpha }_{1}}{{\beta }_{2}} - {{\alpha }_{2}}{{\beta }_{1}}} \right), \hfill \\ {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } }}_{0}}( - 1, + 1) = \frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left[ {Q(2)P(1){{e}^{{ - i{{{\varphi }}_{1}}}}} - Q(1)P(2){{e}^{{ - i{{{\varphi }}_{2}}}}}} \right]{{\alpha }_{1}}{{\alpha }_{2}}, \hfill \\ {{\psi }_{{ - 1}}}( - 1,0) = \frac{1}{2}\left[ {Q(2)P(1){{e}^{{ - i{{{\varphi }}_{1}}}}} - Q(1)P(2){{e}^{{ - i{{{\varphi }}_{2}}}}}} \right]\left( {{{\alpha }_{1}}{{\beta }_{2}} + {{\alpha }_{2}}{{\beta }_{1}}} \right), \hfill \\ {{\psi }_{{ - 2}}}( - 1, - 1) = \frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left[ {Q(2)P(1){{e}^{{ - i{{{\varphi }}_{1}}}}} - Q(1)P(2){{e}^{{ - i{{{\varphi }}_{2}}}}}} \right]{{\beta }_{1}}{{\beta }_{2}}, \hfill \\ \end{gathered} \right.$

где

$Q(k) = Q({{r}_{k}},{{z}_{k}}),$ $P(k) = P({{r}_{k}},{{z}_{k}});$ $k = 1,2.$

Для вычисления электронного гамильтониана в представлении диабатического базиса (12) целесообразно найти матричные представления операторов симметрии (2)–(4) с последующей формулировкой вибронных операторов симметрии [2, 9]. С учетом ортогональности и нормированности базисных состояний (12) мы приходим к следующим ниже результатам.

А. Вибронный оператор симметрии, соответствующий повороту системы вокруг оси z на угол ε, можно представить в виде

(13)
$\hat {G}_{z}^{{{v}ib}}(\varepsilon ) = \left| {\begin{array}{*{20}{c}} {{{e}^{{2i{\varepsilon }}}}}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {} \\ {}&\vline & {{{e}^{{i{\varepsilon }}}}}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {} \\ {}&\vline & {}&\vline & 1&\vline & {}&\vline & {}&\vline & {}&\vline & {} \\ {}&\vline & {}&\vline & {}&\vline & 1&\vline & {}&\vline & {}&\vline & {} \\ {}&\vline & {}&\vline & {}&\vline & {}&\vline & 1&\vline & {}&\vline & {} \\ {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {{{e}^{{ - i{\varepsilon }}}}}&\vline & {} \\ {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {{{e}^{{ - 2i{\varepsilon }}}}} \end{array}} \right|\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{\psi }_{2}}} \\ {{{\psi }_{1}}} \\ {{{\psi }_{0}}} \end{array}} \\ {\begin{array}{*{20}{c}} {{{{\bar {\psi }}}_{0}}} \\ {{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } }}_{0}}} \\ {{{\psi }_{{ - 1}}}} \\ {{{\psi }_{{ - 2}}}} \end{array}} \end{array}{{\hat {C}}_{q}}(\varepsilon ),$

где ${{\hat {C}}_{q}}(\varepsilon ){{q}_{ \pm }} = {{e}^{{ \pm i{\varepsilon }}}}{{q}_{ \pm }}.$

Б. Вибронный оператор симметрии, соответствующий отражению в вертикальной плоскости xz, имеет вид

(14)
$\hat {Z}_{\sigma }^{{{v}ib}} = \left| {\begin{array}{*{20}{c}} {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & 1 \\ {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & { - 1}&\vline & {} \\ {}&\vline & {}&\vline & {}&\vline & {}&\vline & 1&\vline & {}&\vline & {} \\ {}&\vline & {}&\vline & {}&\vline & 1&\vline & {}&\vline & {}&\vline & {} \\ {}&\vline & {}&\vline & 1&\vline & {}&\vline & {}&\vline & {}&\vline & {} \\ {}&\vline & { - 1}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {} \\ 1&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {} \end{array}} \right|\begin{array}{*{20}{c}} {{{\psi }_{2}}} \\ {{{\psi }_{1}}} \\ {{{\psi }_{0}}} \\ {{{{\bar {\psi }}}_{0}}} \\ {{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } }}_{0}}} \\ {{{\psi }_{{ - 1}}}} \\ {{{\psi }_{{ - 2}}}} \end{array}{{\hat {\sigma }}_{q}},$

где ${{\hat {\sigma }}_{q}}{{q}_{ \pm }} = {{q}_{ \mp }}.$

В. Оператор обращения времени:

(15)
$\hat {T} = \left| {\begin{array}{*{20}{c}} {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & { - 1} \\ {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & { + 1}&\vline & {} \\ {}&\vline & {}&\vline & {}&\vline & {}&\vline & { - 1}&\vline & {}&\vline & {} \\ {}&\vline & {}&\vline & {}&\vline & { - 1}&\vline & {}&\vline & {}&\vline & {} \\ {}&\vline & {}&\vline & { - 1}&\vline & {}&\vline & {}&\vline & {}&\vline & {} \\ {}&\vline & { + 1}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {} \\ { - 1}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {} \end{array}} \right|\begin{array}{*{20}{c}} {{{\psi }_{2}}} \\ {{{\psi }_{1}}} \\ {{{\psi }_{0}}} \\ {{{{\bar {\psi }}}_{0}}} \\ {{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } }}_{0}}} \\ {{{\psi }_{{ - 1}}}} \\ {{{\psi }_{{ - 2}}}} \end{array}\widehat {{\text{c}}{\text{.c}}{\text{.}}}$

Вибронная матрица 7 × 7, которую мы стремимся найти, должна будет коммутировать с операторами симметрии (13)–(15). Эти требования сокращают число независимых параметров, которые должна содержать искомая вибронная матрица 7 × 7.

РЕЛЯТИВИСТСКИЙ ПСЕВДО-ЭФФЕКТ РЕННЕРА (3Π + 1Σ+) × π

В данной работе мы исходили из того, что матричные элементы блоков 3 × 3, соответствующих вибронному взаимодействию 3Π-состояний, уже получены и описаны в работах [10, 11]. Целью настоящего исследования являются 12 матричных элементов, соответствующих взаимодействию состояний 3Π и 1Σ+. Получив их, мы сможем представить полную вибронную матрицу 7 × 7 для релятивистского псевдо-эффекта Реннера в виде (3Π + 1Σ+) × π. Результаты, полученные в [10, 11], и групповые правила отбора по Jz позволяют представить искомую вибронную матрицу 7 × 7 в следующем виде:

(16)
$\begin{gathered} \hat {H} = ({}^{3}\Pi + C{{\rho }^{2}}){\text{diag}}(1,1,1,0,1,1,1) + ({}^{1}{{\Sigma }^{ + }} + D{{\rho }^{2}}){\text{diag}}(0,0,0,1,0,0,0) + \hfill \\ + \,\,\begin{array}{*{20}{c}} {\left| {\begin{array}{*{20}{c}} {\Delta + \varepsilon {{\rho }^{2}}}&\vline & {\alpha {{q}_{ - }}}&\vline & {}&\vline & {\delta q_{ - }^{2}}&\vline & {cq_{ - }^{2}}&\vline & {}&\vline & {} \\ {\alpha {{q}_{ + }}}&\vline & {}&\vline & {\alpha {{q}_{ - }}}&\vline & {\gamma {{q}_{ - }}}&\vline & {}&\vline & {cq_{ - }^{2}}&\vline & {} \\ {}&\vline & {\alpha {{q}_{ + }}}&\vline & { - \Delta - \varepsilon {{\rho }^{2}}}&\vline & \beta &\vline & {}&\vline & {}&\vline & {cq_{ - }^{2}} \\ {\delta {\text{*}}q_{ + }^{2}}&\vline & {\gamma {\text{*}}{{q}_{ + }}}&\vline & {\beta {\text{*}}}&\vline & {}&\vline & {\beta {\kern 1pt} '\,*}&\vline & {\gamma {\kern 1pt} '\,*{{q}_{ - }}}&\vline & {\delta {\kern 1pt} '\,*q_{ - }^{2}} \\ {cq_{ + }^{2}}&\vline & {}&\vline & {}&\vline & {\beta {\kern 1pt} '}&\vline & { - \Delta - \varepsilon {{\rho }^{2}}}&\vline & { - \alpha {{q}_{ - }}}&\vline & {} \\ {}&\vline & {cq_{ + }^{2}}&\vline & {}&\vline & {\gamma {\kern 1pt} '{{q}_{ + }}}&\vline & { - \alpha {{q}_{ + }}}&\vline & {}&\vline & { - \alpha {{q}_{ - }}} \\ {}&\vline & {}&\vline & {cq_{ + }^{2}}&\vline & {\delta {\kern 1pt} 'q_{ + }^{2}}&\vline & {}&\vline & { - \alpha {{q}_{ + }}}&\vline & {\Delta + \varepsilon {{\rho }^{2}}} \end{array}} \right|} \\ {\begin{array}{*{20}{c}} {{{\psi }_{2}}}{ {{\psi }_{1}}}{ {{\psi }_{0}}}{ {{{\bar {\psi }}}_{0}}}{ {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } }}_{0}}}{ {{\psi }_{{ - 1}}}}{ {{\psi }_{{ - 2}}}} \end{array} } \end{array}\begin{array}{*{20}{c}} {{{\psi }_{2}}} \\ {{{\psi }_{1}}} \\ {{{\psi }_{0}}} \\ {{{{\bar {\psi }}}_{0}}} \\ {{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } }}_{0}}} \\ {{{\psi }_{{ - 1}}}} \\ {\begin{array}{*{20}{c}} {{{\psi }_{{ - 2}}}} \\ {} \end{array}} \end{array}, \hfill \\ \end{gathered} $

где параметры β, β', γ, γ', δ, δ' считаются пока комплексными, тогда как α, ε, c, C, D, согласно результатам [10, 11], являются вещественными. Требование коммутации матрицы (16) с оператором обращения времени (15) ведет к следующим соотношениям между параметрами:

$\beta {\kern 1pt} ' = \beta *,\,\,\,\,\gamma {\kern 1pt} ' = - \gamma *,\,\,\,\,\delta {\kern 1pt} ' = \delta {\text{*}}.$

Коммутация с оператором отражения в вертикальной плоскости (14) дает три соотношения:

$\beta * = \beta ,\,\,\,\,\gamma * = \gamma ,\,\,\,\,\delta * = \delta ,$

которые означают вещественность параметров β, γ, δ.

Коммутация с оператором поворота (13) не ведет к дополнительным соотношениям между параметрами и удовлетворяется автоматически. В итоге мы приходим к следующей вибронной матрице релятивистского псевдо-эффекта Реннера (3Π + 1Σ+) × π:

(17)
$\begin{gathered} \hat {H} = ({}^{3}\Pi + C{{\rho }^{2}}){\text{diag}}(1,1,1,0,1,1,1) + ({}^{1}{{\Sigma }^{ + }} + D{{\rho }^{2}}){\text{diag}}(0,0,0,1,0,0,0) + \\ + \,\,\begin{array}{*{20}{c}} {\left| {\begin{array}{*{20}{c}} {\Delta + \varepsilon {{\rho }^{2}}}&\vline & {\alpha {{q}_{ - }}}&\vline & {}&\vline & {\delta q_{ - }^{2}}&\vline & {cq_{ - }^{2}}&\vline & {}&\vline & {} \\ {\alpha {{q}_{ + }}}&\vline & {}&\vline & {\alpha {{q}_{ - }}}&\vline & {\gamma {{q}_{ - }}}&\vline & {}&\vline & {cq_{ - }^{2}}&\vline & {} \\ {}&\vline & {\alpha {{q}_{ + }}}&\vline & { - \Delta - \varepsilon {{\rho }^{2}}}&\vline & \beta &\vline & {}&\vline & {}&\vline & {cq_{ - }^{2}} \\ {\delta q_{ + }^{2}}&\vline & {\gamma {{q}_{ + }}}&\vline & \beta &\vline & {}&\vline & \beta &\vline & { - \gamma {{q}_{ - }}}&\vline & {\delta q_{ - }^{2}} \\ {cq_{ + }^{2}}&\vline & {}&\vline & {}&\vline & \beta &\vline & { - \Delta - \varepsilon {{\rho }^{2}}}&\vline & { - \alpha {{q}_{ - }}}&\vline & {} \\ {}&\vline & {cq_{ + }^{2}}&\vline & {}&\vline & { - \gamma {{q}_{ + }}}&\vline & { - \alpha {{q}_{ + }}}&\vline & {}&\vline & { - \alpha {{q}_{ - }}} \\ {}&\vline & {}&\vline & {cq_{ + }^{2}}&\vline & {\delta q_{ + }^{2}}&\vline & {}&\vline & { - \alpha {{q}_{ + }}}&\vline & {\Delta + \varepsilon {{\rho }^{2}}} \end{array}} \right|} \\ {\begin{array}{*{20}{c}} {{{\psi }_{2}}}{{{\psi }_{1}}}{{{\psi }_{0}}}{{{{\bar {\psi }}}_{0}}}{ {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } }}_{0}}}{ {{\psi }_{{ - 1}}}}{ {{\psi }_{{ - 2}}}} \end{array} } \end{array}\begin{array}{*{20}{c}} {{{\psi }_{2}}} \\ {{{\psi }_{1}}} \\ {{{\psi }_{0}}} \\ {{{{\bar {\psi }}}_{0}}} \\ {{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } }}_{0}}} \\ {{{\psi }_{{ - 1}}}} \\ {\begin{array}{*{20}{c}} {{{\psi }_{{ - 2}}}} \\ {} \end{array}} \end{array} , \\ \end{gathered} $

где ${{\rho }^{2}} = {{q}_{ + }}{{q}_{ - }};$ электростатические параметры c, C, D и спин-орбитальные параметры α, β, γ, δ, ∆, ε являются вещественными постоянными. Эти параметры не определяются по свойствам симметрии электронного гамильтониана и для их определения требуется проведение ab initio расчетов точек потенциальных поверхностей молекулы.

ПРЕОБРАЗОВАНИЕ ВИБРОННОЙ МАТРИЦЫ К БАЗИСУ ТИПА BODY-FIXED. ПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ

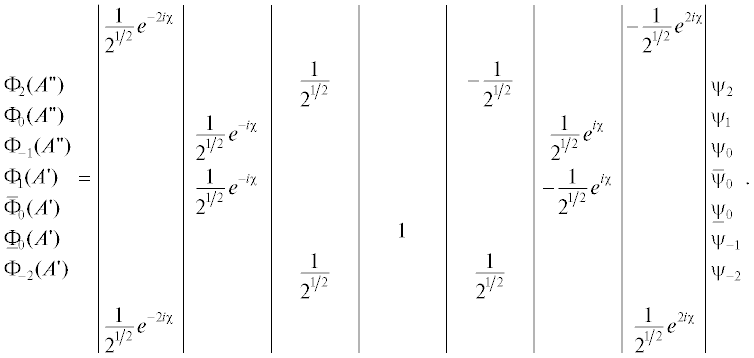
Вибронная матрица (17) представлена в диабатическом базисе (12) типа space-fixed. При ${{q}_{ \pm }} \ne 0$ молекулярной группой симметрии является группа Cs, содержащая тождественную операцию и отражение в плоскости изогнутой трехатомной молекулы и характеризующаяся неприводимыми представлениями A' и A". Поэтому вибронная матрица (17) приобретает наиболее простой вид в базисе электронных состояний A'- и A"-симметрии. Этот базис связан с плоскостью изогнутой молекулы и в международных терминах имеет наименование “body-fixed”. В рассматриваемом случае унитарное преобразование подобия к новому базису осуществляется с помощью матрицы $\hat {S},$ которая имеет следующий вид:

$\hat {S} = \left| {\begin{array}{*{20}{c}} {\frac{1}{{{{2}^{{1/2}}}}}{{e}^{{ - 2i\chi }}}}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {\frac{1}{{{{2}^{{1/2}}}}}{{e}^{{ - 2i\chi }}}} \\ {}&\vline & {}&\vline & {\frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{e}^{{ - i{\chi }}}}}&\vline & {\frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{e}^{{ - i{\chi }}}}}&\vline & {}&\vline & {}&\vline & {} \\ {}&\vline & {\frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}}&\vline & {}&\vline & {}&\vline & {}&\vline & {\frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}}&\vline & {} \\ {}&\vline & {}&\vline & {}&\vline & {}&\vline & 1&\vline & {}&\vline & {} \\ {}&\vline & { - \frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}}&\vline & {}&\vline & {}&\vline & {}&\vline & {\frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}}&\vline & {} \\ {}&\vline & {}&\vline & {\frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{e}^{{i{\chi }}}}}&\vline & { - \frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{e}^{{i{\chi }}}}}&\vline & {}&\vline & {}&\vline & {} \\ {\frac{{ - 1}}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{e}^{{2i{\chi }}}}}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {}&\vline & {\frac{1}{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{e}^{{2i{\chi }}}}} \end{array}} \right|.$

Преобразованная вибронная матрица имеет блочно-диагональный вид и не зависит от угла χ:

(18)
$\begin{gathered} \hat {\tilde {H}} = {{{\hat {S}}}^{ + }}\hat {H}\hat {S} = \\ = \begin{array}{*{20}{c}} {\left| {\begin{array}{*{20}{c}} {\Delta + \varepsilon {{\rho }^{2}}}&\vline & { - c{{\rho }^{2}}}&\vline & {\alpha \rho }&\vline & {}&\vline & {}&\vline & {}&\vline & {} \\ { - c{{\rho }^{2}}}&\vline & { - \Delta - \varepsilon {{\rho }^{2}}}&\vline & {\alpha \rho }&\vline & {}&\vline & {}&\vline & {}&\vline & {} \\ {\alpha \rho }&\vline & {\alpha \rho }&\vline & {c{{\rho }^{2}}}&\vline & {}&\vline & {}&\vline & {}&\vline & {} \\ {}&\vline & {}&\vline & {}&\vline & { - c{{\rho }^{2}}}&\vline & {{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\gamma \rho }&\vline & {\alpha \rho }&\vline & {\alpha \rho } \\ {}&\vline & {}&\vline & {}&\vline & {{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\gamma \rho }&\vline & {}&\vline & {{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\beta }&\vline & {{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\delta {{\rho }^{2}}} \\ {}&\vline & {}&\vline & {}&\vline & {\alpha \rho }&\vline & {{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\beta }&\vline & { - \Delta - \varepsilon {{\rho }^{2}}}&\vline & {c{{\rho }^{2}}} \\ {}&\vline & {}&\vline & {}&\vline & {\alpha \rho }&\vline & {{{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\delta {{\rho }^{2}}}&\vline & {c{{\rho }^{2}}}&\vline & {\Delta + \varepsilon {{\rho }^{2}}} \end{array}} \right|\begin{array}{*{20}{c}} {{{\Phi }_{2}}} \\ {{{\Phi }_{0}}} \\ {{{\Phi }_{{ - 1}}}} \\ {{{\Phi }_{1}}} \\ {{{{\bar {\Phi }}}_{0}}} \\ {{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Phi } }}_{0}}} \\ {{{\Phi }_{{ - 2}}}} \end{array} } \\ {\begin{array}{*{20}{l}} {{{\Phi }_{2}}}&{{{\Phi }_{0}}}&{ {{\Phi }_{{ - 1}}}}&{ {{\Phi }_{1}}}&{ {{{\bar {\Phi }}}_{0}}}&{ {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Phi } }}_{0}}}&{ {{\Phi }_{{ - 2}}}} \end{array}} \end{array} + \\ + \,\,({}^{3}\Pi + C{{\rho }^{2}}){\text{diag}}(1,1,1,1,0,1,1) + ({}^{1}{{\Sigma }^{ + }} + D{{\rho }^{2}}){\text{diag}}(0,0,0,0,1,0,0). \\ \end{gathered} $

В вибронной матрице (18) блок 3 × 3 соответствует базису состояний A "-симметрии, блок 4 × 4 – базису состояний A'-симметрии. Функции нового электронного базиса определяются матрицей $\hat {S}$ и имеют следующий вид:

(19)

Очевидно, что базисные состояния (19) не соответствуют каким-либо определенным проекциям полного углового момента Jz на молекулярную ось симметрии z. Базисные состояния (19) не являются диабатическими, так как зависят от угла χ, определяющего положение плоскости изогнутой молекулы. Собственные значения вибронных матриц (17) и (18) совпадают, так как эти матрицы связаны унитарным преобразованием подобия.

Для системы в состоянии A "-симметрии собственные значения (поверхности потенциальной энергии) могут быть представлены аналитическими выражениями:

(20)

Как следует из соотношений (20), параметры 1Σ+-состояния не влияют на потенциальные поверхности A "-симметрии. Потенциальные поверхности A'-состояний являются собственными значениями блока 4 × 4 вибронной матрицы (18). В рассматриваемом случае эти потенциальные поверхности U4(A '), …, U7(A') имеют чрезвычайно громоздкий вид и должны быть исследованы численно при определенных параметрах вибронного взаимодействия.

При линейной конфигурации молекулы (ρ → 0) семь электронных уровней имеют следующие значения:

(21)

Как следует из соотношений (21), при ρ → 0 имеются две пары двукратно вырожденных уровне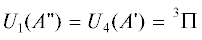й: и 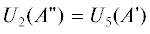= $ = {}^{3}\Pi + \Delta ,$ и три невырожденных уровня – 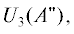${{U}_{6}}(A{\kern 1pt} '),$ ${{U}_{7}}(A{\kern 1pt} ').$

Отметим, что при отсутствии спин-орбитального взаимодействия (т.е. при ρ = 0), имелся бы один шестикратно вырожденный уровень 3Π и один простой уровень 1Σ+. Когда ρ ≠ 0, то при наличии спин-орбитального взаимодействия все уровни являются невырожденными, за исключением некоторых точек, соответствующих пересечению адиабатических термов A'- и A"-состояний.

ЗАКЛЮЧЕНИЕ

Группами симметрии электронного гамильтониана линейной и изогнутой молекул являются соответственно группы C∞v и Cs как в чисто орбитальном анализе, так и с учетом спин-орбитального взаимодействия. Роль последнего заключается в усложнении групповых операторов симметрии, которые обретают матричные факторы и действуют на спиновые операторы гамильтониана.

Для двухэлектронной модели минимальный электронный диабатический базис релятивистского псевдо-эффекта Реннера (3Π + 1Σ+) × π включает в себя семь базисных функций. Линейные электростатические вклады в вибронную матрицу 7 × 7 отсутствуют; имеются только постоянные и квадратичные по π-модам вклады (вклады более высоких порядков не рассматривались).

Спин-орбитальное взаимодействие дает постоянные, линейные и квадратичные вклады в вибронную матрицу. Вибронное взаимодействие между 3Π- и 1Σ+-состояниями обусловлено только спин-орбитальной частью электронного гамильтониана.

Отметим, что вибронное Π–Σ-взаимодействие состояний одинаковой мультиплетности является в основном электростатическим [12]. В базисе состояний A "- и A'-симметрии вибронная матрица и ее собственные значения (поверхности потенциальной энергии) являются аксиально-симметричными, т.е. зависят только от $\rho = {{({{q}_{ + }}{{q}_{ - }})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ При этом вибронная матрица имеет блочный вид с блоками 3 × 3 (A"-состояния) и 4 × 4 (A'-состояния).

Если линейная конфигурация молекулы устойчива, то потенциальные кривые возрастают при увеличении ρ. При этом возможны пересечения A'- и A"-состояний. Точки такого типа (наряду с ρ = 0) ответственны за неадиабатические переходы, генерируемые колебательным угловым моментом [10, 13].

Работа выполнена в рамках госзадания (регистрационные номера АААА-А19-119071190017-7 и АААА-А19-119120690042-9).

Список литературы

  1. Ошеров В.И., Полуянов Л.В. // Теорет. и эксперим. химия. 1978. Т. 14. № 5. С. 590.

  2. Osherov V.I., Osherov M.V., Poluyanov L.V. // Chem. Phys. Lett. 2018. V. 692. P. 232.

  3. Poluyanov L.V., Domcke W. // Adv. Ser. Phys. Chem. 2011. V. 17. P. 117.

  4. Poluyanov L.V., Domcke W. // Springer Ser. Chem. Phys. 2009. V. 97. P. 77.

  5. Ошеров В.И., Полуянов Л.В., Ушаков В.Г. // Хим. физика. 2018. Т. 37. № 1. С. 3.

  6. Банкер Ф., Йенсен П. Симметрия молекул и спектроскопия. Пер. с англ. / Под ред. Степанова Н.Ф. М.: Мир, Научный мир, 2004.

  7. Ландау Л.Д., Лифшиц Е.М. Квантовая механика. М.: Наука, 1974.

  8. Вигнер Е. Теория групп. М.: Изд-во иностр. лит., 1961.

  9. Poluyanov L.V., Domcke W. // J. Chem. Phys. 2012. V. 137. № 13. 114101.

  10. Mishra S., Poluyanov L.V., Domcke W. // J. Chem. Phys. 2007. V. 126. № 13. P. 134312.

  11. Mishra S., Domcke W., Poluyanov L.V. // Chem. Phys. Lett. 2007. V. 446. P. 256.

  12. Köppel H., Domcke W., Cederbau L.S. // J. Chem. Phys. 1981. V. 74. № 5. P. 2945.

  13. Poluyanov L.V., Domcke W. // Chem. Phys. 2004. V. 301. P. 111.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Химическая физика

Архивы выпусков Информация о журнале Отправить рукопись в журнал