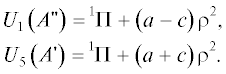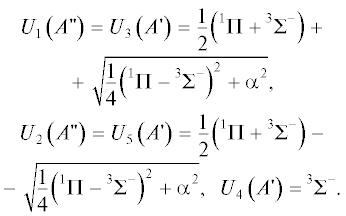Химическая физика, 2021, T. 40, № 5, стр. 3-8
Синглет-триплетное взаимодействие термов 1Π и 3Σ– в линейных трехатомных молекулах
Л. В. Полуянов 1, В. Г. Ушаков 1, *
1 Институт проблем химической физики Российской академии наук
Черноголовка, Россия
* E-mail: uvg@icp.ac.ru
Поступила в редакцию 24.07.2020
После доработки 04.08.2020
Принята к публикации 20.08.2020
Аннотация
В работе получена вибронная матрица, описывающая синглет-триплетное взаимодействие термов 1Π и 3Σ– в линейных трехатомных молекулах. Анализ проведен с учетом спин-орбитального взаимодействия в электронном гамильтониане и основан на использовании его свойств симметрии. Показано, что операторы симметрии электронного гамильтониана содержат как пространственные операции (действующие на координаты электронов), так и матричные (действующие на электронные спины). В работе учитываются только деформационные π-моды, и полученная вибронная матрица $5 \times 5$ фактически описывает релятивистский псевдо-эффект Реннера $\left( {^{1}{{\Pi }}{{ + }^{3}}{{{{\Sigma }}}^{ - }}} \right) \times \pi .$ Собственные значения вибронной матрицы (т.е. поверхности потенциальной энергии) являются инвариантами группы ${{C}_{{\infty {v}}}}.$ Вибронная матрица содержит пять параметров, имеющих электростатическое происхождение, и пять параметров, обусловленных спин-орбитальным взаимодействием.
ВВЕДЕНИЕ
Потенциальные поверхности электронных состояний, имеющих различную пространственную симметрию и мультиплетность, могут пересекаться в симметричных конфигурациях молекулы. При учете спин-орбитального взаимодействия молекулярный спин и проекция орбитального углового момента на молекулярную ось (в случае линейных молекул) не сохраняются, и упомянутые электронные состояния взаимодействуют. В результате поведение потенциальных поверхностей и характер вырождения в окрестности пересечения нерелятивистских термов качественным образом изменяются [1–4].
В данной работе мы рассматриваем модель взаимодействия изолированных по энергии термов 1Π и 3Σ– в линейных трехатомных молекулах, учитывающую спин-орбитальное взаимодействие и описывающую зависимость потенциальных поверхностей от деформационных π-мод [5]. Целью работы было определение общего вида вибронной матрицы. Структура этой матрицы и правила отбора для матричных элементов определяются только свойствами симметрии системы и соответствующими квантовыми числами [6]. Это обстоятельство позволяет упростить анализ, заменив реальную молекулу модельной системой с такой же молекулярной симметрией. В нашей работе мы применяем двухэлектронную модель со специальным выбором диабатических базисных функций, описанных ниже. Полученная в результате двухэлектронная модель взаимодействия термов 1Π и 3Σ– может быть применена и к многоэлектронным линейным трехатомным молекулам с четным числом электронов. При этом вибронные матрицы для различных конкретных молекул отличаются только значениями входящих в эти матрицы постоянных параметров [7].
Рассматриваемая в работе модель спин-орбитального взаимодействия термов 1Π и 3Σ– в пренебрежении взаимодействием с другими электронными состояниями молекулы описывает релятивистский псевдо-эффект Реннера $\left( {^{1}{{\Pi }}{{ + }^{3}}{\kern 1pt} {{{{\Sigma }}}^{ - }}} \right) \times \pi .$ Полученная вибронная матрица может быть применена к изучению интеркомбинационных переходов типа $^{1}{{\Pi }} \leftrightarrows {{\,}^{3}}{\kern 1pt} {{{{\Sigma }}}^{ - }}$ в линейных трехатомных молекулах XCN (X = Cl, Br, I) [8].
ДВУХЭЛЕКТРОННЫЙ ГАМИЛЬТОНИАН И ЕГО СИММЕТРИЯ
Основным релятивистским эффектом в реннеровских системах является спин-орбитальное взаимодействие. С учетом последнего электронный гамильтониан представляем в виде суммы двух операторов – электростатического гамильтониана ${{\hat {H}}_{{es}}}$ и гамильтониана спин-орбитального взаимодействия ${{\hat {H}}_{{so}}}$ [6, 7, 9, 10]:
где
(2)
${{\hat {H}}_{{es}}} = - \frac{{{{\hbar }^{2}}}}{{2{{m}_{e}}}}\nabla _{1}^{2} - \frac{{{{\hbar }^{2}}}}{{2{{m}_{e}}}}\nabla _{2}^{2} - \sum\limits_{\unicode{230} = 1}^3 {\sum\limits_{k = 1}^2 {\frac{{e{{Z}_{\unicode{230} }}}}{{{{R}_{{k\unicode{230} }}}}} + \frac{{{{e}^{2}}}}{{{{R}_{{12}}}}}} } $и
(3)
$\begin{gathered} {{{\hat {H}}}_{{so}}} = - ig{{\mu }^{2}}\sum\limits_{k,\unicode{230} } {\frac{{{{Z}_{\unicode{230} }}}}{{R_{{k\unicode{230} }}^{3}}}} {{{{\mathbf{\hat {S}}}}}_{k}}\left[ {{{{\mathbf{R}}}_{{k\unicode{230} }}} \times {{\nabla }_{k}}} \right] + \frac{{ig{{\mu }^{2}}}}{{2R_{{12}}^{3}}} \times \\ \times \,\,\left\{ {{{{\mathbf{S}}}_{1}}\left[ {{{{\mathbf{R}}}_{{12}}}\left( {{{\nabla }_{1}} - 2{{\nabla }_{2}}} \right)} \right] + {{{\mathbf{S}}}_{2}}\left[ {{{{\mathbf{R}}}_{{21}}}\left( {{{\nabla }_{2}} - 2{{\nabla }_{1}}} \right)} \right]} \right\}. \\ \end{gathered} $В формулах (2) и (3) номера ядер обозначены индексом “$\unicode{230} $”, номера электронов – индексом “k”, либо числами 1 и 2; ${{{\mathbf{R}}}_{{k\unicode{230} }}} = {{{\mathbf{R}}}_{k}} - {{{\mathbf{R}}}_{\unicode{230} }},$ ${{{\mathbf{R}}}_{{12}}} = {{{\mathbf{R}}}_{1}} - {{{\mathbf{R}}}_{2}};$ $g = 2.0023$ – g-фактор свободного электрона, $\mu = {{e\hbar } \mathord{\left/ {\vphantom {{e\hbar } {2{{m}_{e}}c}}} \right. \kern-0em} {2{{m}_{e}}c}}$ – магнетон Бора.
В линейной конфигурации молекулы электронный гамильтониан (1) характеризуется точечной группой симметрии ${{C}_{{\infty {v}}}}.$ Операторы этой группы, коммутирующие с гамильтонианом $\hat {H},$ имеют вид
(5)
$\hat {G}_{z}^{{{\varepsilon }}} = {{\hat {C}}_{1}}\left( \varepsilon \right){{\hat {C}}_{2}}\left( \varepsilon \right){{\left( {\begin{array}{*{20}{c}} {{{e}^{{{{i{{\varepsilon }}} \mathord{\left/ {\vphantom {{i{{\varepsilon }}} 2}} \right. \kern-0em} 2}}}}}&0 \\ 0&{{{e}^{{{{ - i{{\varepsilon }}} \mathord{\left/ {\vphantom {{ - i{{\varepsilon }}} 2}} \right. \kern-0em} 2}}}}} \end{array}} \right)}_{1}}{{\left( {\begin{array}{*{20}{c}} {{{e}^{{{{i{{\varepsilon }}} \mathord{\left/ {\vphantom {{i{{\varepsilon }}} 2}} \right. \kern-0em} 2}}}}}&0 \\ 0&{{{e}^{{{{ - i{{\varepsilon }}} \mathord{\left/ {\vphantom {{ - i{{\varepsilon }}} 2}} \right. \kern-0em} 2}}}}} \end{array}} \right)}_{2}},$(6)
${{\hat {Z}}_{{{\sigma }}}} = \hat {\sigma }_{{xz}}^{{\left( 1 \right)}}\hat {\sigma }_{{xz}}^{{\left( 2 \right)}}{{\left( {\begin{array}{*{20}{c}} 0&1 \\ { - 1}&0 \end{array}} \right)}_{1}}{{\left( {\begin{array}{*{20}{c}} 0&1 \\ { - 1}&0 \end{array}} \right)}_{2}}.$В формулах (4)–(6) индексы “1” и “2” у операторов указывают, на какой электрон в электронном гамильтониане действует данный оператор. Пространственно-матричные двухэлектронные операторы $\hat {G}_{z}^{{{\varepsilon }}}$ и ${{\hat {Z}}_{{{\sigma }}}}$ соответствуют повороту системы координат на угол $\varepsilon $ вокруг молекулярной оси $z$ $\left( {\hat {G}_{z}^{{{\varepsilon }}}} \right)$ и отражению в плоскости $xz$ $\left( {{{{\hat {Z}}}_{{{\sigma }}}}} \right).$ Они действуют как на координаты электронов, так и на операторы электронных спинов (на матрицы Паули) в электронном гамильтониане $\hat {H}.$ Помимо этих пространственно-матричных операторов симметрии, электронный гамильтониан $\hat {H}$ характеризуется еще одним оператором симметрии – антиунитарным оператором обращения времени $\hat {T}$ [11, 12], коммутирующим с $\hat {H}{\text{:}}$
(7)
$\hat {T} = {{\left( {\begin{array}{*{20}{c}} 0&{ - i} \\ i&0 \end{array}} \right)}_{1}}{{\left( {\begin{array}{*{20}{c}} 0&{ - i} \\ i&0 \end{array}} \right)}_{2}}\widehat {{\text{c}}{\text{.c}}},$где $\widehat {{\text{c}}{\text{.c}}}$ – оператор комплексного сопряжения. Для рассматриваемой модели с четным числом электронов имеет место соотношение ${{\hat {T}}^{2}} = 1.$
РАЗЛОЖЕНИЕ ЭЛЕКТРОННОГО ГАМИЛЬТОНИАНА В РЯД ТЕЙЛОРА
Разложение электронного гамильтониана в ряд Тейлора по π-модам удобно вести в терминах величин, принадлежащих неприводимым представлениям группы молекулярной симметрии ${{C}_{{\infty {v}}}}$ с групповыми операциями (4)–(6). В табл. 1 приведены соответствующие симметризованные комбинации нормальных мод и матриц Паули вплоть до вкладов второго порядка по π-модам. Разложение электростатического гамильтониана в ряд Тейлора имеет вид
Таблица 1.
Симметризованные комбинации нормальных мод и матриц Паули
| Порядок | Номера симметризованных комбинаций | Симметрия | Тип нормальной моды и матриц Паули | Симметризованные комбинации |
|---|---|---|---|---|
| Первый орбитальный | 1 | $\pi $ | $q$ | ${{q}_{ + }} = {{q}_{x}} + i{{q}_{y}},$${{q}_{ - }} = {{q}_{x}} - i{{q}_{y}}$ |
| Второй орбитальный | 2 | ${{\sigma }^{ + }}$ | $qq$ | ${{q}_{ + }}~{{q}_{ - }}$ |
| 3 | $\delta $ | $qq$ | $q_{ + }^{2},$$q_{ - }^{2}$ | |
| Нулевой спин-орбитальный | 4, 5 | ${{\sigma }^{ - }}$ | $\sigma $ | $\hat {\sigma }_{z}^{{\left( 1 \right)}},$$\hat {\sigma }_{z}^{{\left( 2 \right)}}$ |
| 6 | $\pi $ | $\sigma $ | $\hat {\sigma }_{ + }^{{\left( 1 \right)}} = {{\left( {\hat {\sigma }_{y}^{{\left( 1 \right)}} - i\hat {\sigma }_{x}^{{\left( 1 \right)}}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {\sigma }_{y}^{{\left( 1 \right)}} - i\hat {\sigma }_{x}^{{\left( 1 \right)}}} \right)} 2}} \right. \kern-0em} 2},$$\hat {\sigma }_{ - }^{{\left( 1 \right)}} = {{\left( {\hat {\sigma }_{y}^{{\left( 1 \right)}} + i\hat {\sigma }_{x}^{{\left( 1 \right)}}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {\sigma }_{y}^{{\left( 1 \right)}} + i\hat {\sigma }_{x}^{{\left( 1 \right)}}} \right)} 2}} \right. \kern-0em} 2}$ | |
| 7 | $\hat {\sigma }_{ + }^{{\left( 2 \right)}} = {{\left( {\hat {\sigma }_{y}^{{\left( 2 \right)}} - i\hat {\sigma }_{x}^{{\left( 2 \right)}}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {\sigma }_{y}^{{\left( 2 \right)}} - i\hat {\sigma }_{x}^{{\left( 2 \right)}}} \right)} 2}} \right. \kern-0em} 2},$$\hat {\sigma }_{ - }^{{\left( 2 \right)}} = {{\left( {\hat {\sigma }_{y}^{{\left( 2 \right)}} + i\hat {\sigma }_{x}^{{\left( 2 \right)}}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {\sigma }_{y}^{{\left( 2 \right)}} + i\hat {\sigma }_{x}^{{\left( 2 \right)}}} \right)} 2}} \right. \kern-0em} 2}$ | |||
| Первый спин-орбитальный, $k = 1,2$ | 8, 9 | ${{\sigma }^{ + }}$ | $q\sigma $ | ${{q}_{ - }}\hat {\sigma }_{ + }^{{\left( k \right)}} + {{q}_{ + }}\hat {\sigma }_{ - }^{{\left( k \right)}}$ |
| 10, 11 | ${{\sigma }^{ - }}$ | $q\sigma $ | ${{q}_{ - }}\hat {\sigma }_{ + }^{{\left( k \right)}} - {{q}_{ + }}\hat {\sigma }_{ - }^{{\left( k \right)}}$ | |
| 12, 13 | $\pi $ | $q\sigma $ | ${{q}_{ + }}\hat {\sigma }_{z}^{{\left( k \right)}},$$ - {{q}_{ - }}\hat {\sigma }_{z}^{{\left( k \right)}}$ | |
| 14, 15 | $\delta $ | $q\sigma $ | ${{q}_{ + }}\hat {\sigma }_{ + }^{{\left( k \right)}},$${{q}_{ - }}\hat {\sigma }_{ - }^{{\left( k \right)}}$ | |
| Второй спин-орбитальный, $k = 1,2$ | 16, 17 | ${{\sigma }^{ - }}$ | ${{q}^{2}}\sigma $ | ${{q}_{ + }}{{q}_{ - }}\hat {\sigma }_{z}^{{\left( k \right)}}$ |
| 18, 19 | $\pi $ | ${{q}^{2}}\sigma $ | ${{q}_{ + }}{{q}_{ - }}\hat {\sigma }_{ + }^{{\left( k \right)}},$${{q}_{ + }}{{q}_{ - }}\hat {\sigma }_{ - }^{{\left( k \right)}}$ | |
| 20, 21 | $\pi $ | ${{q}^{2}}\sigma $ | $q_{ + }^{2}\hat {\sigma }_{ - }^{{\left( k \right)}},$$q_{ - }^{2}\hat {\sigma }_{ + }^{{\left( k \right)}}$ | |
| 22, 23 | $\delta $ | ${{q}^{2}}\sigma $ | $q_{ + }^{2}\hat {\sigma }_{z}^{{\left( k \right)}},$$q_{ - }^{2}\hat {\sigma }_{z}^{{\left( k \right)}}$ | |
| 24, 25 | ${{\Phi }}$ | ${{q}^{2}}\sigma $ | $q_{ + }^{2}\hat {\sigma }_{ + }^{{\left( k \right)}},$$q_{ - }^{2}\hat {\sigma }_{ - }^{{\left( k \right)}}$ |
где ${{\hat {H}}_{0}}$ – электростатический гамильтониан линейной молекулы,
(9)
${{\hat {H}}_{1}} = {{\hat {H}}_{ + }}\left( {{{\pi }_{ - }}} \right){{q}_{ + }} + {{\hat {H}}_{ - }}\left( {{{\pi }_{ + }}} \right){{q}_{ - }},$(10)
${{\hat {H}}_{2}} = {{\hat {H}}_{{ + + }}}\left( {{{\delta }_{ - }}} \right)q_{ + }^{2} + {{\hat {H}}_{{ - - }}}\left( {{{\delta }_{ + }}} \right)q_{ - }^{2} + {{\hat {H}}_{{ + - }}}\left( {{{\sigma }^{ + }}} \right){{q}_{ + }}{{q}_{ - }},$${{q}_{ \pm }} = \rho ~{\text{exp}}\left( { \pm i\chi } \right)$ – нормальные π-моды, записанные в симметричной комплексной форме.
В терминах симметризованных комбинаций из табл. 1 ряд Тейлора для спин-орбитального взаимодействия выглядит следующим образом:
где
(12)
$\begin{gathered} {{{\hat {h}}}_{0}} = \sum\limits_{k = 1,2} {\left[ {{}^{k}{{{\hat {h}}}_{ + }}\left( {{{\pi }_{ - }}} \right)\hat {\sigma }_{ + }^{{\left( k \right)}} + {{\,}^{k}}{{{\hat {h}}}_{ - }}\left( {{{\pi }_{ + }}} \right)\hat {\sigma }_{ - }^{{\left( k \right)}} + } \right.} \\ \left. { + {{\,}^{k}}{{{\hat {h}}}_{z}}\left( {{{\sigma }^{ - }}} \right)\hat {\sigma }_{z}^{{\left( k \right)}}} \right], \\ \end{gathered} $(13)
$\begin{gathered} {{{\hat {h}}}_{1}} = \sum\limits_{k = 1,2} {\left[ {^{k}\hat {h}_{ + }^{ + }\left( {{{\delta }_{ - }}} \right){{q}_{ + }}\hat {\sigma }_{ + }^{{\left( k \right)}} + {{\,}^{k}}\hat {h}_{ - }^{ - }\left( {{{\delta }_{ + }}} \right){{q}_{ - }}\hat {\sigma }_{ - }^{{\left( k \right)}} + } \right.} \\ + \,{{\,}^{k}}{{{\hat {h}}}^{ + }}\left( {{{\sigma }^{ + }}} \right)\left( {{{q}_{ - }}\hat {\sigma }_{ + }^{{\left( k \right)}} + {{q}_{ + }}\hat {\sigma }_{ - }^{{\left( k \right)}}} \right) + {{\,}^{k}}{{{\hat {h}}}^{ - }}\left( {{{\sigma }^{ - }}} \right) \times \\ \left. { \times \,\,\left( {{{q}_{ - }}\hat {\sigma }_{ + }^{{\left( k \right)}} - {{q}_{ + }}\hat {\sigma }_{ - }^{{\left( k \right)}}} \right) + {{\,}^{k}}\hat {h}_{z}^{ + }\left( {{{\pi }_{ - }}} \right){{q}_{ + }}\hat {\sigma }_{z}^{{\left( k \right)}} - {{\,}^{k}}\hat {h}_{z}^{ - }\left( {{{\pi }_{ + }}} \right){{q}_{ - }}\hat {\sigma }_{z}^{{\left( k \right)}}} \right], \\ \end{gathered} $(14)
$\begin{gathered} {{{\hat {h}}}_{2}} = \sum\limits_{k = 1,2} {\left\{ {\left[ {{}_{{}}^{k}\hat {h}_{ + }^{{ + + }}\left( {{{{{\Phi }}}_{ - }}} \right)q_{ + }^{2} + {}_{{}}^{k}\hat {h}_{ + }^{{ - - }}\left( {{{{{\pi }}}_{ + }}} \right)q_{ - }^{2} + } \right.} \right.} \\ \left. { + \,{{\,}^{k}}\hat {h}_{ + }^{{ + - }}\left( {{{{{\pi }}}_{ - }}} \right){{q}_{ + }}{{q}_{ - }}} \right]\hat {\sigma }_{ + }^{{\left( k \right)}} + \left[ {^{k}\hat {h}_{ - }^{{ + + }}\left( {{{{{\pi }}}_{ - }}} \right)q_{ + }^{2} + {{\,}^{k}}\hat {h}_{ - }^{{ - - }} \times } \right. \\ \times \,\,\left. {\left( {{{{{\Phi }}}_{ + }}} \right)q_{ - }^{2} + {{\,}^{k}}\hat {h}_{ - }^{{ + - }}\left( {{{{{\pi }}}_{ + }}} \right){{q}_{ + }}{{q}_{ - }}} \right]\hat {\sigma }_{ - }^{{\left( k \right)}} + \\ + \,\,\left[ {^{k}\hat {h}_{z}^{{ + + }}\left( {{{{{\delta }}}_{ - }}} \right)q_{ + }^{2} - {{\,}^{k}}\hat {h}_{z}^{{ - - }}\left( {{{{{\delta }}}_{ + }}} \right)q_{ - }^{2} + {{\,}^{k}}\hat {h}_{z}^{{ + - }}\left( {{{\sigma }^{ - }}} \right){{q}_{ + }}{{q}_{ - }}} \right]\hat {\sigma }_{z}^{{\left( k \right)}}. \\ \end{gathered} $Каждый операторный коэффициент рядов Тейлора (8)–(11) преобразуется по неприводимому представлению и его строчке, которые указаны в качестве аргументов этих коэффициентов. Подчеркнем, что все операторные коэффициенты рядов Тейлора (8)–(11) преобразуются по неприводимым представлениям, которые комплексно сопряжены неприводимым представлениям соответствующих симметризованных комбинаций. В соответствии с [11] данная симметрия операторных коэффициентов обеспечивает необходимую инвариантность в группе ${{C}_{{\infty {v}}}}$ операторов ${{\hat {H}}_{i}}$ ($i = 1,~2$) и ${{\hat {h}}_{j}}$ ($j = 1,~2,~3$).
ДИАБАТИЧЕСКИЙ БАЗИС ЭЛЕКТРОННЫХ СОСТОЯНИЙ
Ниже мы используем цилиндрические координаты, в которых ось $z$ направлена вдоль оси линейной молекулы, $r$ – цилиндрический радиус и $\varphi $ – угол поворота вокруг оси z. Введем далее две молекулярные Π-орбитали $P\left( {r,z} \right){\text{exp}}\left( { \pm i\varphi } \right)$ и одну Σ+-орбиталь $Q\left( {r,z} \right).$ Диабатический базис двухэлектронных спин-орбиталей ${{{{\Psi }}}_{i}},$ $i = 1, \ldots ,5,$ записываем в порядке неувеличения проекции на ось $z$ полного углового момента ${{J}_{z}} = {{L}_{z}} + {{S}_{z}}{\text{:}}$
(15)
$\begin{gathered} {{{{\Psi }}}_{1}} = \frac{1}{2}\left[ {P\left( 1 \right)Q\left( 2 \right){{e}^{{i{{{{\varphi }}}_{1}}}}} + P\left( 2 \right)Q\left( 1 \right){{e}^{{i{{{{\varphi }}}_{2}}}}}} \right]\left( {{{\alpha }_{1}}{{\beta }_{2}} - {{\alpha }_{2}}{{\beta }_{1}}} \right), \\ {{{{\Psi }}}_{2}} = \frac{1}{{\sqrt 2 }}P\left( 1 \right)P\left( 2 \right)\left[ {{{e}^{{i{{{{\varphi }}}_{1}} - i{{{{\varphi }}}_{2}}}}} - {{e}^{{ - i{{{{\varphi }}}_{1}} + i{{{{\varphi }}}_{2}}}}}} \right]{{\alpha }_{1}}{{\alpha }_{2}}, \\ {{{{\Psi }}}_{3}} = \frac{1}{2}P\left( 1 \right)P\left( 2 \right)\left[ {{{e}^{{i{{{{\varphi }}}_{1}} - i{{{{\varphi }}}_{2}}}}} - {{e}^{{ - i{{{{\varphi }}}_{1}} + i{{{{\varphi }}}_{2}}}}}} \right]\left( {{{\alpha }_{1}}{{\beta }_{2}} + {{\alpha }_{2}}{{\beta }_{1}}} \right), \\ {{{{\Psi }}}_{4}} = \frac{1}{{\sqrt 2 }}P\left( 1 \right)P\left( 2 \right)\left[ {{{e}^{{i{{{{\varphi }}}_{1}} - i{{{{\varphi }}}_{2}}}}} - {{e}^{{ - i{{{{\varphi }}}_{1}} + i{{{{\varphi }}}_{2}}}}}} \right]{{\beta }_{1}}{{\beta }_{2}}, \\ {{{{\Psi }}}_{5}} = \frac{1}{2}\left[ {P\left( 1 \right)Q\left( 2 \right){{e}^{{ - i{{{{\varphi }}}_{1}}}}} + P\left( 2 \right)Q\left( 1 \right){{e}^{{ - i{{{{\varphi }}}_{2}}}}}} \right]\left( {{{\alpha }_{1}}{{\beta }_{2}} - {{\alpha }_{2}}{{\beta }_{1}}} \right). \\ \end{gathered} $Здесь использованы следующие обозначения:
Для вычисления электронного гамильтониана в представлении диабатического базиса (15) целесообразно найти матричные представления операторов симметрии (4)–(7) с последующим определением вибронных операторов симметрии [5, 13]. С учетом ортогональности и нормированности базисных состояний (15) мы приходим к представленным ниже результатам.
А. Единичный двухэлектронный оператор (4) в базисе (15) приобретает форму единичной матрицы $5 \times 5.$
Б. Вибронный оператор поворота вокруг оси $z$ на угол $\varepsilon - $
(16)
$\begin{gathered} \hat {G}_{z}^{{{v}ib}}\left( \varepsilon \right) = \\ = \left\| {\begin{array}{*{20}{c}} {{\text{exp}}\left( {i\varepsilon } \right)}&{}&{}&{}&{} \\ {}&{{\text{exp}}\left( {i\varepsilon } \right)}&{}&{}&{} \\ {}&{}&1&{}&{} \\ {}&{}&{}&{{\text{exp}}\left( { - i\varepsilon } \right)}&{} \\ {}&{}&{}&{}&{{\text{exp}}\left( { - i\varepsilon } \right)} \end{array}} \right\|{{{\hat {C}}}_{q}}\left( \varepsilon \right), \\ \end{gathered} $где ${{\hat {C}}_{q}}\left( \varepsilon \right)~{{q}_{ \pm }}$ = $\exp \left( { \pm i\varepsilon } \right){{q}_{ \pm }}.$
В. Вибронный оператор отражения в плоскости $xz - $
(17)
$\hat {Z}_{{{\sigma }}}^{{{v}ib}} = \left\| {\begin{array}{*{20}{c}} {}&{}&{}&{}&1 \\ {}&{}&{}&{ - 1}&{} \\ {}&{}&1&{}&{} \\ {}&{ - 1}&{}&{}&{} \\ 1&{}&{}&{}&{} \end{array}} \right\|{{\hat {\sigma }}_{q}},$где ${{\hat {\sigma }}_{q}}{{q}_{ \pm }} = {{q}_{ \mp }}.$
Г. Оператор обращения времени –
(18)
$\hat {T} = \left\| {\begin{array}{*{20}{c}} {}&{}&{}&{}&{ - 1} \\ {}&{}&{}&1&{} \\ {}&{}&{ - 1}&{}&{} \\ {}&1&{}&{}&{} \\ { - 1}&{}&{}&{}&{} \end{array}} \right\|\widehat {{\text{c}}{\text{.c}}}.$Вибронная матрица $5 \times 5$ гамильтониана должна коммутировать с операторами симметрии (16)–(18). Эти требования уменьшают число независимых параметров, которые остаются в искомой вибронной матрице после применения групповых правил отбора для матричных элементов.
РЕЛЯТИВИСТСКИЙ ПСЕВДО-ЭФФЕКТ РЕННЕРА $\left( {^{1}{\mathbf{\Pi }} + {{\,}^{3}}{{\Sigma }^{ - }}} \right) \times \pi $
Правила отбора для электронного гамильтониана в базисе (15) по квантовому числу проекции полного углового момента ${{J}_{z}} = {{L}_{z}} + {{S}_{z}},$ а также требования коммутации вибронной матрицы с операторами симметрии (16)–(18) приводят к вибронной матрице следующего вида:
(19)
$\hat {H} = \left\| {\begin{array}{*{20}{c}} {^{1}{{\Pi }} + a{{\rho }^{2}}}&\alpha &{\beta {{q}_{ - }}}&{\delta q_{ - }^{2}}&{cq_{ - }^{2}} \\ \alpha &{^{3}{{{{\Sigma }}}^{ - }} + b{{\rho }^{2}}}&{\gamma {{q}_{ - }}}&{\varepsilon q_{ - }^{2}}&{ - \delta q_{ - }^{2}} \\ {\beta {{q}_{ + }}}&{\gamma {{q}_{ + }}}&{^{3}{{{{\Sigma }}}^{ - }} + b{{\rho }^{2}}}&{ - \gamma {{q}_{ - }}}&{\beta {{q}_{ - }}} \\ {\delta q_{ + }^{2}}&{\varepsilon q_{ + }^{2}}&{ - \gamma {{q}_{ + }}}&{^{3}{{{{\Sigma }}}^{ - }} + b{{\rho }^{2}}}&{ - \alpha } \\ {cq_{ + }^{2}}&{ - \delta q_{ + }^{2}}&{\beta {{q}_{ + }}}&{ - \alpha }&{^{1}{{\Pi }} + a{{\rho }^{2}}} \end{array}} \right\|,$где $^{1}{{\Pi ,}}$ $^{3}{{{{\Sigma }}}^{ - }},$ $a,b,c$ – электростатические параметры; $\alpha ,\beta ,\gamma ,\delta ,\varepsilon $ – параметры, обусловленные спин-орбитальным взаимодействием. Отметим, что в двухэлектронной модели параметры $\alpha ,\delta ,\varepsilon $ оказываются равными нулю, что является специфичным именно для этой модели. Поэтому мы сохраняем эти параметры в вибронной матрице (19), имея в виду приложения этой матрицы к изучению многоэлектронных систем, содержащих тяжелые, существенно релятивистские атомы.
Вибронная матрица (19) представлена в диабатическом базисе (15), функции которого
соответствуют определенным значениям проекции полного момента на ось линейной молекулы.
При отклонении от линейности, т.е. при ${{q}_{ \pm }} \ne 0,$ молекулярной группой симметрии является группа ${{C}_{s}},$ содержащая тождественную операцию и операцию отражения в плоскости изогнутой трехатомной
молекулы и характеризующаяся неприводимыми представлениями $A{\kern 1pt} '$ и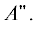 
Поэтому при ${{q}_{ \pm }} \ne 0$ вибронная матрица приобретает наиболее простой вид в базисе электронных состояний
симметрии $A{\kern 1pt} '$ и 
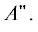Этот базис связан с диабатическим базисом (15) унитарным преобразованием подобия,
зависящим от пространственного положения (от угла $\chi $) плоскости изогнутой молекулы и имеющим вид [14]
где вектор-столбцы ${\mathbf{\Phi }}$ и ${\mathbf{\Psi }}$ связаны транспонированной матрицей $\hat {S}{\text{:}}$
При этом преобразованная вибронная матрица не зависит от угла $\chi $ и имеет блок-диагональный вид (с блоками $2 \times 2$ и $3 \times 3$):
(20)
$\hat {\tilde {H}} = {{\hat {S}}^{T}}\hat {H}\hat {S} = \left\| {\begin{array}{*{20}{c}} {^{1}{{\Pi }} + \left( {a - c} \right){{\rho }^{2}}}&{\alpha + \delta {{\rho }^{2}}}&0&0&0 \\ {\alpha + \delta {{\rho }^{2}}}&{^{3}{{{{\Sigma }}}^{ - }} + \left( {b + \varepsilon } \right){{\rho }^{2}}}&0&0&0 \\ 0&0&{^{3}{{{{\Sigma }}}^{ - }} + \left( {b - \varepsilon } \right){{\rho }^{2}}}&{\sqrt 2 \gamma \rho }&{\alpha - \delta {{\rho }^{2}}} \\ 0&0&{\sqrt 2 \gamma \rho }&{^{3}{{{{\Sigma }}}^{ - }} + b{{\rho }^{2}}}&{\sqrt 2 \beta \rho } \\ 0&0&{\alpha - \delta {{\rho }^{2}}}&{\sqrt 2 \beta \rho }&{^{1}{{\Pi }} + \left( {a + c} \right){{\rho }^{2}}} \end{array}} \right\|.$Действуя оператором отражения ${{\hat {Z}}_{{{\sigma }}}}$ (уравнение (6)) на функции ${{{{\Phi }}}_{k}},$ $k = 1, \ldots ,5,$ находим, что базисные функции ${{{{\Phi }}}_{1}}$ и ${{{{\Phi }}}_{2}}$ имеют симметрию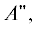 
тогда как состояния ${{{{\Phi }}}_{3}},$ ${{{{\Phi }}}_{4}}$ и ${{{{\Phi }}}_{5}}$ характеризуются симметрией $A{\kern 1pt} '.$ Собственные значения (поверхности потенциальной энергии) блока 2 × 2 электронных
состояний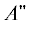 
представляются простыми аналитическими выражениями, в то время как собственные значения
блока 3 × 3 электронных состояний $A{\kern 1pt} '$ являются решениями кубического уравнения и представляются выражениями громоздкого
вида, которые мы здесь не приводим.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
В пренебрежении спин-орбитальным взаимодействием вибронная матрица (20) имеет диагональный вид:
При этом имеется трехкратно вырожденный по проекции спина уровень орбитальной симметрии
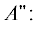
в то время как двукратно вырожденный в линейной конфигурации Π-терм благодаря орбитальному
эффекту Реннера расщепляется на два состояния с орбитальной симметрией $A{\kern 1pt} '$ и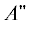 
[8]:
Таким образом, четыре состояния имеют орбитальную симметрию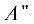 
и одно состояние – симметрию $A{\kern 1pt} '.$ При учете спин-орбитального взаимодействия операторы симметрии (5)–(7) необходимо
включают в себя матричные факторы, и в системе имеется два состояния спин-орбитальной
симметрии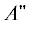 
и три – $A{\kern 1pt} '.$
Как следует из соотношений (21) и (22), электростатические уровни энергии системы
в линейной конфигурации включают в себя двукратно вырожденный уров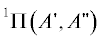ень 
и трехкратный уровень $^{3}{{{{\Sigma }}}^{ - }}\left( {3A{\kern 1pt} ''} \right).$ Спин-орбитальное взаимодействие приводит к частичному снятию вырождения, и в линейной
конфигурации имеется два двукратно вырожденных уровня и один однократный уровень:
При отклонении от линейной конфигурации термы, имеющие в ней значения, определяемые
уравнениями (23), расщепляются, и вырождение снимается полностью. При этом потенциальные кривые состояний
различной симметрии, $A{\kern 1pt} '$ и 
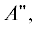могут пересекаться, а состояния одинаковой симметрии могут испытывать квазипересечения.
Колебательный угловой момент π-мод обуславливает вращение плоскости молекулы, смешивает
состояния симметрий $A{\kern 1pt} '$ и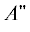 
и генерирует неадиабатические переходы между ними в точках вырождения как при $\rho = 0,$ так и при $\rho > 0$ [15, 16].
Работа выполнена по теме госзадания (регистрационный номер АААА-А19-119071190017-7).
Список литературы
Волохов В.М., Полуянов Л.В. // Хим. физика. 2020. Т. 39. № 3. С. 9; https://doi.org/10.31857/S0207401X20030140
Полуянов Л.В., Волохов В.М. // Хим. физика. 2018. Т. 37. № 11. С. 3; https://doi.org/10.1134/S0207401X18100096
Полуянов Л.В., Волохов В.М. // Хим. физика. 2017. Т. 36. № 11. С. 10; https://doi.org/10.7868/S0207401X17110061
Ошеров В.И., Полуянов Л.В. // Теорет. и эксперим. химия. 1978. Т. 14. № 5. С. 590.
Osherov V.I., Osherov M.V., Poluyanov L.V. // Chem. Phys. Let. 2018. V. 692. P. 232.
Poluyanov L.V., Domcke W. // Conical Intersections / Eds. Domcke W., Yarkony D.R., Köeppel H. Adv. Ser. Phys. Chem. 2011. V. 17. P. 117.
Poluyanov L.V., Domcke W. // The Jahn-Teller effect / Eds. Koeppel H., Yarkony D.R., Barentzen H. Springer Ser. Chem. Phys. 2009. V. 97. P. 77.
Герцберг Г. Электронные спектры и строение многоатомных молекул. М.: Мир, 1969.
Ошеров В.И., Полуянов Л.В., Ушаков В.Г. // Хим. физика. 2018. Т. 37. № 1. С. 3; https://doi.org/10.7868/S0207401X18010107
Банкер Ф. Симметрия молекул и молекулярная спектроскопия. М.: Мир, 1981.
Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нерелятивистская теория. М.: Наука, 1974.
Вигнер Е. Теория групп. М.: Изд-во иностр. лит., 1961.
Poluyanov L.V., Domcke W. // J. Chem. Phys. 2012. V. 137. P. 114101.
Koeppel H., Domcke W., Cederbaum L.S. // Ibid. 1981. V. 74. № 5. P. 2945.
Mishra S., Poluyanov L.V., Domcke W. // Ibid. 2007. V. 126. P. 134312.
Poluyanov L.V., Domcke W. // Chem. Phys. 2004. V. 301. P. 111.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика
Пн.-пт.: 10.00-19.00