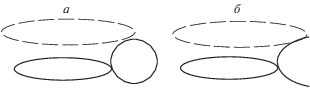Химическая физика, 2021, T. 40, № 7, стр. 85-90

1. ВВЕДЕНИЕ

Точность позиционирования глобальных навигационных спутниковых систем (GNSS) определяется различными источниками ошибок, приводящих к сбою в работе GNSS. В первую очередь к ним относятся: ошибка определения орбиты спутника, ошибка часов спутника и ионосферная задержка сигнала. Для уменьшения влияния этих ошибок широко используются системы внешней коррекции (SBAS) [1], которые передают исправления ошибок в реальном времени с геостационарных спутников. Системы SBAS используют сигналы, совместимые с глобальной системой позиционирования (GPS), что упрощает добавление возможностей приема сигнала SBAS к приемникам GPS без значительных модификаций оборудования. Современные алгоритмы, используемые в SBAS, достаточно хорошо справляются с ошибками орбиты/часов спутника. В то же время проблема корректного учета ионосферной задержки вплоть до настоящего времени остается открытой [1].

Ранее традиционно считалось, что основной вклад в задержку спутникового сигнала дают рассеяние и дифракция спутникового сигнала на ионосферных неоднородностях в F-слое ионосферы [2]. Однако последние теоретические исследования резонансных квантовых свойств D- и E-слоев ионосферы [3–5] показали, что ключевую роль в задержке сигналов GPS играют вибронные автоионизационные состояния ридберговских комплексов. В работе [6] было установлено, что частоты оптических переходов между состояниями орбитально вырожденных ридберговских комплексов являются резонансными по отношению к несущим частотам GPS и ответственны за задержки сигналов GPS. Квантовый механизм задержки сигнала в D- и E-слоях ионосферы был подробно рассмотрен в работе [4]. Прямые измерения с помощью баллистических ракет [7] и радиозатменным методом [8] подтвердили, что слой атмосферы, где преимущественно происходит деградация сигнала, расположен на высоте от 60 до 110 км над поверхностью Земли, т.е. в D- и E-слоях ионосферы. В этой связи возникает нетривиальная проблема адекватного теоретического описания квантовой динамики временнóй задержки спутниковых сигналов. Именно этому посвящено проведенное нами исследование, в котором проанализированы возможности геометрической интерпретации квантовой механики и установлен смысл “скрытых параметров” теории.

Под интерпретацией квантовой механики подразумевается объяснение необычных свойств микромира, хорошо описываемых ее математическим аппаратом, на языке привычных понятий. Подробное обсуждение проблемы и исчерпывающий список публикаций на эту тему представлены в работе [9]. Заметим, что В.Л. Гинзбург считал такую интерпретацию одной из “трех великих задач”, стоящих перед физикой (наряду с объяснением феномена жизни и необратимой стрелы времени) [10]. Возникает вопрос: зачем нужна какая-то интерпретация математического аппарата теории, хорошо согласующейся с экспериментом? Главная причина заключается в том, что новые физические модели всегда открывали новые возможности для развития теории. По этой причине, например, было предпринято много попыток (Эйнштейном, Вейлем, Калуцей и др.) найти геометрическую интерпретацию классической электродинамики, хотя она очень хорошо согласуется с экспериментом [11, 12]. Так и в данном случае, хорошее согласие квантовой механики с опытом не означает, что она способна ответить на все вопросы, а ее аппарат не нуждается в усовершенствовании.

В рамках существующего аппарата определение спектра простейшего многоэлектронного атома, атома гелия, уже требует значительных усилий. Трудности вычисления спектров многоэлектронных атомов и молекул усложняют решение многих практически важных задач – например, задачи о прохождении электромагнитных сигналов через атмосферу. С другой стороны, ранее было показано, что геометрические модели могут оказаться полезными при вычислении атомных спектров [13]. Другая причина – это не получившая окончательного разрешения полемика Эйнштейна и Бора о том, является ли квантовая механика полной теорией [14, 15]. В отличие от Бора Эйнштейн считал квантовую механику неполной теорией, поскольку в ее формализме не отражены элементы физической реальности, ответственные за статистический характер теории (так называемые “скрытые параметры”). Что касается физических моделей, то к настоящему времени известна лишь одна интерпретация квантовой механики, в которой ее математический аппарат не подвергается изменению. Это “теория множественных миров Эверетта”, где вероятностный характер наблюдений за квантовыми объектами объясняется одновременным существованием бесконечного числа “параллельных” Вселенных, соответствующих различным возможным реализациям наблюдаемых событий [16]. Несмотря на экзотический характер и серьезную критику, эта интерпретация имеет своих сторонников [10].

В прошлом столетии значительное внимание исследователей было уделено и проблеме “скрытых параметров”. Тем не менее окончательно к единому мнению им прийти не удалось (см., например, [17, 18]). В настоящей работе предлагается интерпретация математического аппарата квантовой механики на языке понятий, доступных нашему сознанию, а именно, показана возможность интерпретировать волновую функцию свободной частицы как описание микроскопического искажения геометрии пространства-времени. Определенные характеристики этого геометрического объекта описывают существующие до измерения свойства физической реальности, ответственные за стохастическое поведение отдельной частицы. Другие геометрические характеристики объекта объясняют корпускулярно-волновой дуализм этой частицы. Можно сказать, что в рамках предложенной геометрической интерпретации квантовая механика удовлетворяет критерию полноты теории, сформулированному в свое время Эйнштейном. Следует указать также на предварительные результаты, которые были опубликованы ранее в работах [13, 19–21].

2. ВОЛНОВАЯ ФУНКЦИЯ КАК ОПИСАНИЕ МИКРОСКОПИЧЕСКОГО ИСКАЖЕНИЯ ГЕОМЕТРИИ ПРОСТРАНСТВА-ВРЕМЕНИ

Рассмотрим теперь движение свободной нейтральной частицы с массой $m$ и нулевым спином. Покажем, что волновую функцию такой частицы можно проинтерпретировать как математическое описание определенного геометрического объекта. Волновая функция рассматриваемой частицы описывается уравнением Клейна–Фока–Гордона и имеет вид [22]

В рамках существующей интерпретации квантовой механики такая функция описывает состояние, в котором частица обладает определенной энергией $~E~$ и импульсом p. В этом состоянии положение частицы в пространстве до измерения не определено, т.е. с равной вероятностью она может быть обнаружена в любой точке. Это обстоятельство отражает статистический характер квантовой механики – одно из ее необычных свойств с точки зрения классической физики. Другое свойство квантовой теории – это интерпретация волновой функции как описания наблюдаемых на опыте корпускулярно-волновых свойств частицы (дифракция и интерференция), которые определяются фазой, длиной волны и частотой этой функции, связанными с энергией и импульсом частицы соотношениями [22, 23]

После подстановки (2) в (1) волновая функция (если вектор p направлен вдоль оси x) принимает вид

Функции такого вида (плоская волна) широко используются в классической физике (например, при описании плоской бегущей звуковой волны). В рамках существующей (копенгагенской) интерпретации квантовой механики вопрос о происхождении описываемого функцией (3) волнового процесса на языке понятий, доступных сознанию (что же именно колеблется?), считается вопросом, не имеющим смысла, как и вопрос о происхождении статистических свойств квантовых частиц.

Запишем функцию (1) не в пространственно-временных координатах $x,y,z,t,$ а только в пространственных координатах ${{x}^{1}},~{{x}^{2}},{{x}^{3}},{{x}^{4}}$ пространства событий специальной теории относительности – четырехмерного псевдоевклидового пространства индекса 1 (пространства Минковского [24, 25]). В этом пространстве время, умноженное на скорость света, играет роль четвертой пространственной координаты указанного пространства: $ct = {{x}^{4}}.$ С этой целью, используя релятивистские обозначения и единицы ($\hbar = c = 1$), перепишем (1) в виде

Здесь ${{p}_{{{\mu }}}}$ – 4-импульс частицы (${{p}_{1}} = E,$ ${{p}_{{2,3,4}}} = {{p}_{{x,y,z}}}$). По повторяющимся индексам в (4) проводится суммирование с сигнатурой ($ + - - - $). В релятивистском случае [22]

Запишем окончательно (4) так, чтобы это выражение содержало только величины с размерностью длины, т.е.

где

В отличие от (1) и (3) функция (6) не имеет вида плоской волны, а представляет собой периодическую функцию четырех пространственных декартовых координат в пространстве Минковского.

Функцию (6) можно рассматривать как функцию, реализующую представление группы, элементами которой являются дискретные трансляции вдоль четырех координатных направлений в пространстве Минковского. Действительно, функция (6) переходит в саму себя при трансляциях вида

где ${{n}_{{{\mu }}}}$ – целые числа (μ = 1, 2, 3, 4). Эта группа эквивалентна (изоморфна) группе, элементами которой являются произведения целых чисел ${{n}_{{{\mu }}}}$ (в топологии эта группа обозначается как ${{\mathbb{Z}}^{4}},$ где $\mathbb{Z}~$обозначает группу целых чисел). Известно, что группа ${{\mathbb{Z}}^{4}}~$ эквивалентна (изоморфна) так называемой фундаментальной группе замкнутого четырехмерного многообразия, гомеоморфного четырехмерному тору ${{T}^{4}}$ [26, 27]. Понятие “гомеоморфно” означает, что этот геометрический объект задан с точностью до любых деформаций тора ${{T}^{4}}$ без разрывов и склеиваний [26, 27]. Фундаментальная группа – это группа замкнутых путей на многообразии, начинающихся и оканчивающихся в одной и той же точке многообразия [26, 27] (ниже мы разъясним эти понятия подробнее).

Изложенное выше позволяет сформулировать следующую гипотезу. Описываемую волновой функцией (6) квантовую частицу можно рассматривать на геометрическом языке как замкнутое четырехмерное топологическое многообразие, гомеоморфное четырехмерному тору, вложенному в пятимерное псевдоевклидово пространство индекса 1. Соотношение (7) накладывает метрическое ограничение на допустимые при деформациях дли́ны путей ${{\lambda }_{i}}~$ (i = 1, 2, 3, 4). Соотношение (7) определяет также геометрическую интерпретацию массы и 4-импульса. Далее будет показано, что в трехмерном евклидовом пространстве такой геометрический объект реализуется как двигающийся топологический дефект этого пространства, обладающий статистическими и корпускулярно-волновыми свойствами квантовой частицы. Здесь необходимо отметить, что геометрия четырехмерных замкнутых топологических многообразий находится в стадии развития: даже для трехмерных замкнутых многообразий полного алгоритма их распознавания до сих пор не построено [27]. Поэтому единственный возможный способ пояснить, что означает представление квантовой частицы как “замкнутого” 4-многообразия, является использование низкомерных аналогий.

Коротко напомним о понятиях замкнутого топологического многообразия и его фундаментальной группы. Главное отличие замкнутого топологического многообразия от “обычных” геометрических фигур заключается в том, что такое многообразие определено с точностью до произвольной его деформации без разрывов и склеиваний [26, 27]. Окружность и квадрат – это одно и то же замкнутое многообразие: две из бесконечного множества замкнутых фигур, которые можно получить деформацией окружности. Можно условно сказать, что замкнутое многообразие “существует одновременно” в виде всех его возможных деформаций (его гомеоморфизмов). Несмотря на произвольность формы, замкнутые многообразия обладают специфическим видом симметрии, проявляющейся в том, что число различных типов замкнутых путей, начинающихся и оканчивающихся в одной и той же точке, на различных многообразиях может быть различным. Например, у всех деформаций окружности один тип замкнутых путей, а у всех деформаций обычного двухмерного тора два типа замкнутых путей (соответствующих “меридианам” и “параллелям” тора). Для сложных многообразий эти различные типы путей при сложении снова дают замкнутые пути, т.е. они образуют группу, которая называется фундаментальной группой замкнутых многообразий [26, 27].

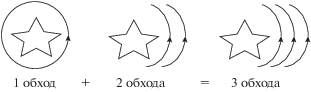
На рис. 1 в рамках одномерной аналогии объясняется смысл фундаментальной группы замкнутого многообразия, гомеоморфного окружности. На этом рисунке изображен один из бесчисленного множества возможных гомеоморфизмов окружности, при этом результат не зависит от конкретного выбора. Замкнутые пути на этом одномерном многообразии образуют группу целых чисел – фундаментальную группу одномерного замкнутого многообразия, гомеоморфного окружности. В данном случае различные классы замкнутых путей фундаментальной группы – это n-кратные обходы по замкнутой кривой, которые можно складывать как целые числа (строгое доказательство дано в работе [26]). Фиксированная длина обхода является дополнительным метрическим ограничением на возможную длину замкнутого пути данного одномерного многообразия, и такая длина была бы аналогом параметров ${{\lambda }_{{{\mu }}}}$ в выражении (7).

Рис. 1.

Одномерное замкнутое топологическое многообразие, гомеоморфное окружности, и его фундаментальная группа.

Таким образом, представление частицы замкнутым топологическим многообразием означает, что такую частицу до измерения можно рассматривать как “смесь” всех ее возможных геометрических представлений, и только взаимодействие с прибором фиксирует одну из возможных форм. Это означает, что волновая функция описывает не отдельную частицу, а статистический ансамбль всех ее возможных геометрических реализаций, что и объясняет статистический характер квантовой механики. Таким образом, ансамбль всех возможных гомеоморфизмов играет роль “скрытых параметров”, ответственных за стохастическое поведение частицы.

3. КВАНТОВАЯ ЧАСТИЦА КАК ТОПОЛОГИЧЕСКИЙ ДЕФЕКТ ЕВКЛИДОВОГО ПРОСТРАНСТВА

Перейдем к “расшифровке” представления квантовой частицы как замкнутого топологического 4-многообразия, т.е. покажем, как такой геометрический объект выглядит с точки зрения наблюдателя в евклидовом пространстве. Воспользуемся низкомерной аналогией и рассмотрим многообразие, гомеоморфное 2-мерному тору в 3-мерном псевдоевклидовом пространстве индекса 1. Для получения конкретного результата возьмем только один из бесконечного множества возможных гомеоморфизмов этого многообразия, а именно тот, которому соответствует обычный 2 мерный тор ${{T}^{2}} = {{S}^{1}} \times {{S}^{1}},$ где ${{S}^{1}}$ – окружность.

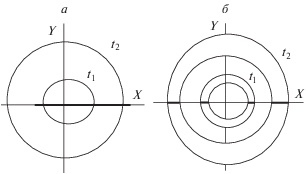
В 3-мерном пространстве такой тор можно рассматривать как поверхность, полученную вращением окружности вокруг вертикальной оси, лежащей в плоскости этой окружности и не пересекающей ее (см. рис. 2а). В 3-мерном псевдоевклидовом пространстве эта окружность расположена в псевдоевклидовой плоскости и на евклидовой плоскости рисунка изображается равнобочной гиперболой [28], т.е. в 3-мерном евклидовом пространстве представляющий частицу 2-мерный тор изображается гиперболоидом (см. рис. 2б). Физическим пространством-временем (пространством событий) в рамках рассматриваемой низкомерной системы является псевдоевклидово 2-мерное пространство, и положения наблюдаемой частицы в разные моменты времени в евклидовом (одномерном) пространстве определяются точками пересечения с этим пространством проекций временны́х сечений гиперболоида (перпендикулярных вертикальной оси времени на рис. 2б). Эти сечения являются расширяющимися окружностями в двумерной евклидовой плоскости XY (см. рис. 3а).

Рис. 2.

Двухмерный тор, вложенный в трехмерное эвклидово и псевдоевклидово пространства.

Рис. 3.

Топологический дефект одномерного евклидового пространства (ось $~X)$.

Эти окружности можно рассматривать как двигающийся топологический дефект одномерного физического пространства, т.е. искажение его геометрии, которое невозможно устранить непрерывным преобразованием координат. Именно принадлежность точки пересечения к топологическому дефекту отличает ее на рис. 3а от соседних точек евклидового одномерного пространства, превращая ее в физическую “материальную” точку.

В предыдущем разделе было отмечено, что в рамках предлагаемого подхода стохастические свойства частицы обусловлены ее представлением в виде “смеси” бесконечного числа возможных гомеоморфизмов топологического многообразия. В рамках рассматриваемой 2-мерной аналогии можно понять, что это означает с точки зрения наблюдателя в евклидовом пространстве. На рис. 3а положение частицы в евклидовом (одномерном) пространстве определяется точкой его пересечения с окружностью, соответствующей лишь одному из бесконечного числа возможных гомеоморфизмов обычного 2-мерного тора. Учет всех возможных гомеоморфизмов приведет, очевидно, к “размазыванию” этой окружности и превращению одной точки пересечения в конечную область евклидового пространства (на рис. 3б эта область пересечения дефекта с евклидовым пространством обозначена жирными отрезками на оси $X$). Сама область имеет конечный размер, так как диапазон возможных гомеоморфизмов задан метрическим условием (7), ограничивающим максимально возможные размеры замкнутого многообразия. В результате наблюдатель в евклидовом пространстве будет обнаруживать частицу с равной вероятностью в одной из точек вышеуказанной области. Это означает, что волновая функция описывает не положение отдельной частицы, а статистический ансамбль ее возможных положений, что объясняет статистический характер квантовой механики. Роль “скрытых параметров”, стохастическая природа которых является причиной статистического описания частицы, играют, как мы видим, все возможные гомеоморфизмы представляющего частицу многообразия, каждому из которых соответствует определенное положение частицы в евклидовом пространстве. Гиперболическая зависимость координаты точки пересечения в евклидовом пространстве от времени означает, что область всех точек пересечения будет, расширяясь, перемещаться на рис. 3б в бесконечность, заполняя все одномерное евклидово пространство. В результате вероятность обнаружить свободную частицу в любой точке пространства окажется одинаковой, как это и должно быть, согласно правилам квантовой механики, для частицы, описываемой волновой функцией (1).

Тот факт, что квантовую частицу можно представить в евклидовом пространстве как точку, “принадлежащую” топологическому дефекту, позволяет объяснить ее корпускулярно-волновые свойства. Для этого достаточно предположить, что в 5-мерном пространстве дефект при движении изменяет свое положение относительно евклидова пространства по периодическому закону, описываемому волновой функцией (1); строгое доказательство этого предположения не представляется возможным в рамках существующей многомерной топологии. Можно сказать, что фаза периодического движения топологического дефекта является дополнительной степенью свободы двигающейся частицы, от которой зависит воздействие частицы на измерительный прибор. Этим и объясняются присущие частице волновые свойства. Корпускулярные свойства частицы (ее 4-импульс) определяются через характеристики периодического движения топологического дефекта известными соотношениями [22, 23]:

Эти соотношения тождественны известному выражению (2) длины волны частицы через ее импульс, но теперь они имеют “обратный” смысл определения импульса через длину волны, как это и должно быть в последовательной теории, где менее общие понятия (классический импульс) определяются через более глубокие квантовые понятия (длина волны колебаний дефекта).

4. РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Проведенный анализ позволяет перейти к обсуждению перспективы использования релятивистской квантовой теории для определения деградации и времени задержки спутниковых сигналов GNNS. Прямым указанием на эту возможность служит работа [29], в которой дано подробное обсуждение особенностей излучения D- и E-слоев ионосферы и формирования ошибок позиционирования приемников спутниковых сигналов. Было показано, что релятивистские ошибки, как правило, не превышают ошибок ионосферных и надежно оцениваются.

Для построения последовательной квантовой теории временнóй задержки следует воспользоваться выражениями (4)–(7) и рассчитать матричные элементы радиационных переходов в электромагнитном поле передатчика между закрытыми каналами автоионизационных вибронных состояний и дискретными состояниями ридберговских комплексов на несущих GNNS-частотах. В результате, согласно [4], задержка сигнала будет определяться характерным временем динамики вибронного обмена между автоионизационными состояниями ридберговских комплексов.

Следующим важным обстоятельством является стохастичность спектров излучения ридберговских комплексов в интересующих нас областях частот [30]. Физическая причина этого обусловлена наличием сильной неадиабатической связи электронного и ядерного движений в ридберговских состояниях молекул [31]. Поскольку эти вопросы выходят за рамки настоящей работы, их исследование планируется выполнить в дальнейшем.

5. ЗАКЛЮЧЕНИЕ

В рамках предложенной геометрической интерпретации показано, что волновая функция свободной частицы (1) играет двоякую роль. Во-первых, она является функцией, реализующей представление группы симметрии “замкнутого” 4-многообразия, представляющего свободную частицу как определенный геометрический объект. Во-вторых, эта функция описывает периодическое движение во внешнем пространстве топологического дефекта, пересечение которого с евклидовым пространством определяет возможные положения частицы. Указанные свойства волновой функции позволяют объяснить корпускулярно-волновой дуализм частицы и ее стохастическое поведение. Роль “скрытых параметров”, ответственных за стохастическое поведение частицы, здесь играют все возможные гомеоморфизмы представляющего частицу замкнутого топологического 4-многообразия.

Работа выполнена в рамках госзадания Министерства науки и высшего образования Российской Федерации (регистрационный номер АААА-А19-119010990034-5).