Химическая физика, 2022, T. 41, № 10, стр. 84-90

1. ВВЕДЕНИЕ

Ионосфера является средой распространения радиоволн. Через ионосферу осуществляются наземная радиосвязь, навигация воздушных и морских судов, радиолокация и пеленгация. Поэтому необходимо предвидеть те, иногда катастрофические, изменения параметров ионосферы, которые приводят к нарушению, а иногда и к полному исчезновению радиосвязи [1]. Электрические поля и токи оказывают значительное влияние на тепловой баланс, динамику и структуру верхней атмосферы на всех широтах [2–5]. Особенно их роль возрастает в периоды магнитосферных возмущений, когда ионосфера испытывает значительные изменения [6–9].

Для того чтобы получить пространственно-временную картину вариаций электрического поля в ионосфере, в каждом конкретном случае данных наблюдений не хватает ни в спокойных условиях, ни тем более во время геомагнитных бурь. Ликвидировать этот недостаток в настоящее время нам помогают самосогласованные модели верхней атмосферы Земли [10, 11]. Одним из основных механизмов переноса плазмы в ионосфере Земли является электромагнитный дрейф, который важно правильно учитывать при моделировании ионосферы, особенно верхней. Для исследования пространственно-временного распределения электрического поля в ионосфере Земли и физических механизмов его генерации разрабатываются численные модели электрического поля в ионосфере. В связи с существованием в ионосфере двух основных типов электрических полей (ионосферного и магнитосферного происхождения) имеется два вида численных моделей: электрического динамо-поля в ионосфере Земли [12–15] и электрического поля магнитосферной конвекции [3, 16–19]. Заметим, что иногда следует учитывать третий источник, а именно глобальную электрическую цепь, связанную с грозовой активностью [20] и полями подземных генераторов [21], электрическое поле которых принимается в расчет только в отдельных случаях, хотя в ночное время оно может иметь важное значение.

В существующих глобальных численных моделях потенциал крупномасштабного электрического поля находится из решения двумерного уравнения электропроводности, которое получается из трехмерного уравнения баланса полного тока в ионосфере интегрированием его вдоль силовых линий геомагнитного поля в предположении, что продольная проводимость бесконечна. Так, например, организован блок расчета потенциала электрического поля в глобальной самосогласованной модели термосферы – ионосферы – протоносферы (ГСМ ТИП) [22–24]. Результаты расчетов по этой модели использовались для интерпретации вариаций ионосферных параметров в спокойных геомагнитных условиях и во время геомагнитных бурь [25–27]. Следует отметить, что в блоке расчета электрического поля модели ГСМ ТИП используется метод решения эллиптического двумерного уравнения для электрического потенциала в ионосфере, который обладает недостаточно высокой точностью и скоростью сходимости. Предварительные оценки показали, что вследствие этого в значительной мере увеличиваются временны́е затраты при проведении численных расчетов по модели ГСМ ТИП. В данной статье мы приводим результаты сравнения точности и быстродействия двух численных алгоритмов расчета электрического потенциала в ионосфере Земли.

2. ПОСТАНОВКА ЗАДАЧИ МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Основными уравнениями для стационарного электрического поля E и плотности тока j в ионосфере Земли, которые мы используем в своих численных моделях, являются уравнения, описывающие закон Фарадея, закон сохранения заряда и закон Ома:

где $\hat {\sigma }$ – тензор проводимости, $q$ – это локальная производная по времени от плотности электрического заряда, приносимого сторонним током, который в стационарном процессе должен быть скомпенсирован током проводимости [28]. Поскольку векторная функция $E$ удовлетворяет уравнению (1), может быть введен электрический потенциал $V,$ такой что

Тогда система уравнений (1)–(3) сводится к уравнению электропроводности:

Трехмерное уравнение (5) приводится к двумерному виду интегрированием по толщине токопроводящего слоя ионосферы вдоль силовых линий геомагнитного поля, проводимость вдоль которых много больше поперечных проводимостей. Решение этого двумерного уравнения мы осуществляем с использованием двух моделей. В первой модели (далее – модель 1 [23]), используемой в модели ГСМ ТИП, решение эллиптического уравнения (5), записанного в разностном виде, осуществляется методом последовательной нижней релаксации при параметре релаксации, равном 0.9. Итерационный процесс осуществляется с наперед заданной точностью 10^–6. Эта модель электрического поля использовалась для исследования влияния атмосферных приливов [29] и магнитосферно-ионосферных токовых систем [24] на распределение электрического потенциала в ионосфере.

Другая модель (далее – модель 2) представлена в работах [30, 31]. В статье [32] описано, как заменить краевую задачу для электрического потенциала в ионосфере задачей с самосопряженным положительно определенным оператором для специальных потенциалов, и доказан принцип минимума квадратичного функционала энергии. Это позволяет минимизировать функционал вместо решения краевой задачи. Этот вариационный принцип полезен для получения приближенного или численного решения, поскольку позволяет использовать многие классические алгоритмы. Численный метод для такой задачи подробно описан в книге [33], включая новую постановку краевой задачи, метод конечных элементов, многосеточный метод и некоторые тестовые расчеты. В методе конечных элементов используются регулярные неоднородные сетки и кусочно-линейные аппроксимирующие функции. Уравнения метода конечных элементов получены в качестве условий минимума функционала энергии. Для решения этой системы линейных алгебраических уравнений используется многосеточный метод Федоренко. Эффективность разработанного многосеточного метода показана при тестировании и расчетах электрических полей и токов в ионосфере Земли, включая модель, представленную в работе [34]. Типичные примеры рассмотрены далее.

3. ОПИСАНИЕ ТЕСТОВЫХ КРАЕВЫХ ЗАДАЧ

Для сравнения численных результатов двух описанных выше моделей с аналитическими решениями нами рассмотрены несколько идеализированных случаев. При моделировании электрического поля в ионосфере Земли чаще всего используются сферические геомагнитные координаты: коширота и долгота, ${{\theta }_{m}},{{\varphi }_{m}};$ при этом геомагнитная широта ${{\lambda }_{m}} = \left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right) - {{\theta }_{m}}.$ Построим некоторую опорную область на плоскости с декартовыми координатами $x,y,$ точки которой идентифицируют все интересующие нас линии магнитного поля [30]. Преобразуем северную полусферу в единичную окружность с полярными координатами (радиус $\rho < 1$ и угол $0 < \alpha < 2\pi $):

Конформно преобразуем полученный круг в полосу $0 < x < 2\pi ,$ $y > 0{\text{:}}$

Поскольку $x = \alpha = {{\varphi }_{m}},$ нас интересует решение, которое является периодическим по $x.$ Построенная полоса не имеет физического смысла, однако она удобна для численного решения и помогает избежать трудностей, связанных с особенностью проводимости в экваториальной ионосфере [35]. В такой полосе после необходимого геометрического преобразования двумерное уравнение электропроводности, полученное из уравнения (5), выглядит следующим образом:

где ${{{{\Sigma }}}_{P}}$ и ${{{{\Sigma }}}_{H}}$ – интегральные проводимости Педерсена и Холла [28], а $Q$ в общем виде определяется тремя источниками. Во-первых, это дивергенция стороннего тока внутри ионосферы, т.е. правая часть уравнения (2), проинтегрированная вдоль магнитной силовой линии. Во-вторых, атмосферные токи $J_{{atm}}^{N}$ и $J_{{atm}}^{S},$ входящие в ионосферу через концы магнитной силовой линии в Северном и Южном полушариях. В-третьих, магнитосферно-ионосферные продольные токи. В рассматриваемых тестовых задачах атмосферные и магнитосфернно-ионосферные токи отсутствуют.

Граница $y$ = 0 соответствует самым низким магнитным силовым линиям, которые рассматриваются как ионосферные. Их вершины находятся на высоте ${{h}_{{eq}}} = 90$ км на геомагнитном экваторе, в то время как их самые низкие точки находятся на высоте ${{h}_{1}} = 80$ км. Это позволяет избежать нулевой длины этих последних линий и связанных с ними нулевых коэффициентов в уравнении (6). Это также делает ненулевой правую часть в граничном условии, полученном из закона сохранения заряда:

где $J_{{eq}}^{0}\left( x \right)$ включает в себя атмосферные токи $J_{{atm}}^{N},$ $J_{{atm}}^{S},$ входящие в ионосферу через самые нижние магнитные силовые лини. Рассмотрение проводников в магнитосфере [31] показывает, что авроральные зоны эквивалентны почти идеальным проводникам, поскольку они соединены параллельно с хорошими магнитосферными проводниками. Мы аппроксимируем их как идеальные проводники с заданным распределением электрического потенциала $V.$ Поэтому граничное условие имеет вид

Дифференциальное уравнение в частных производных (6) является уравнением эллиптического типа, и краевая задача (6)–(8) имеет единственное решение [32].

Интегральные проводимости, рассчитанные на полуденном меридиане при низкой солнечной активности в день весеннего равноденствия, аппроксимируем с помощью следующих формул:

где ${{{{\Sigma }}}_{0}},~\mu ,\beta ,{{\beta }_{e}},{{{{\Sigma }}}_{e}}$ – заданные константы. Для упрощения выкладок предполагаем непрерывность проводимости Холла: $\beta {{{{\Sigma }}}_{0}} = {{\beta }_{e}}{{{{\Sigma }}}_{e}}.$ Слой, соответствующий $y < {{y}_{e}},$ представляет собой узкую полосу вблизи границы $y = 0$ и соответствует области экваториальных электроструй. Мы полагаем ${{y}_{e}} = 0.00615$ и ${{y}_{a}}$ = 1.6265, что соответствует высоте $h = 120$ км и широте 75°, и задаем следующие значения: ${{{{\Sigma }}}_{0}} = 200$ См, β = 1.5, μ = 2, ${{{{\Sigma }}}_{e}} = 10$ См, ${{\beta }_{e}} = 30.$ Последние дают значение проводимости Каулинга ${{{{\Sigma }}}_{C}} = 9010$ См, интеграл которой в области электроструи $90 < h < 120$ км составляет около $270$ МСм · м, как в реальной полуденной ионосфере. Граничные условия (7) и (8) в тесте имеют вид где ${{V}_{0}} = 25$ кВ.

Точное решение задачи (6), (10) мы находим как действительную часть комплексной функции $V\left( {x,y} \right).$

При $0 < y < {{y}_{e}}{\text{:}}$

где i – мнимая единица.

При ${{y}_{e}} < y < {{y}_{a}}$

где

Если исключить область электроструи и определить во всей области

получается более простой тест. Для тех же граничных условий (см. (10)) точное решение имеет вид (11) с теми же ${{\lambda }_{{1,2}}},$ но

Несложно проверить, что это решение получается из предыдущего при ${{y}_{e}} \to 0.$

4. РЕЗУЛЬТАТЫ

Для тестирования двух выбранных нами методов решения уравнения электропроводности для электрического потенциала в ионосфере Земли на точность и быстродействие были рассмотрены пять задач, имеющих точные аналитические решения. Решение двух простейших задач, в первой из которой в формулах (9) используются следующие значения: ${{{{\Sigma }}}_{0}} = 1\,\,{\text{См}},$ $\mu = 0,$ $\beta = 0$ при $0 < y < {{y}_{a}}$ (т.е. Σ_P = 1 См, а Σ_H = 0 См), а во второй ${{{{\Sigma }}}_{0}} = 1\,\,{\text{См}},$ $\mu = 0,$ $\beta = 1.5$ при $0 < y < {{y}_{a}}$ (т.е. Σ_P = 1 См, а Σ_H = = 1.5 См), в данной статье не приводится. Мы лишь отмечаем высокую точность обоих методов при решении этих двух идеализированных задач. При этом точность в методе, используемом в модели 2 выше вблизи экватора в 4–6 раз, а время счета в 3 раза меньше, чем в методе, используемом в модели 1.

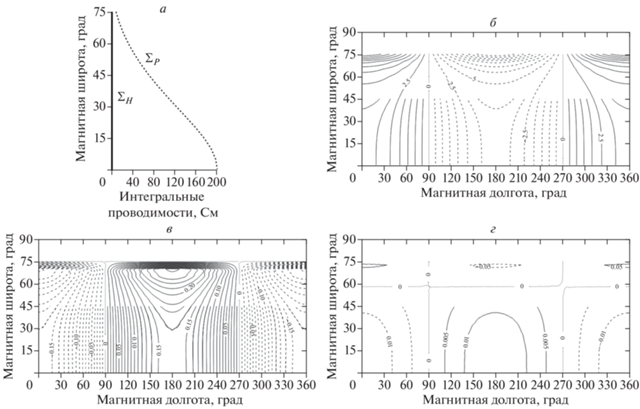
В третьей задаче в формулах (9) рассматривалась область $0 < y < {{y}_{a}}$ при ${{{{\Sigma }}}_{0}} = 200\,\,{\text{См}},$ $\mu = 2,$ $\beta = 0$ (т.е. ${{{{\Sigma }}}_{P}} = 200\exp \left( { - 2y} \right)$, а Σ_H = 0). На рис. 1 показаны для случая 3-ей задачи широтные профили проводимостей Холла и Педерсена и аналитическое решение в отсутствие холловской проводимости и при проводимости Педерсена, изменяющейся по экспоненте от экватора к высоким широтам и постоянной по долготе. На этом же рисунке показаны погрешности моделей 2 и 1 в виде разностей между аналитическим и модельными решениями. Видно, что точность модели 2 в 5–15 раз выше, чем модели 1. Максимальная погрешность модели 1 вблизи экватора составила 0.15 кВ, а в высоких широтах – 0.3 кВ, тогда как погрешность модели 2 там же составила 0.01 кВ и 0.05 кВ соответственно. При этом время счета в 3–5 раз меньше для модели 2 по сравнению с моделью 1.

В четвертой задаче так же, как и в трех предыдущих, в формулах (9) рассматривалась область $0 < y < {{y}_{a}}$ при ${{{{\Sigma }}}_{0}} = 200\,\,{\text{См}},$ $\mu = 2,$ $\beta = 1.5$ (т.е. ${{{{\Sigma }}}_{P}} = 200\exp \left( { - 2y} \right),$ а Σ_H = $~300\exp \left( { - 2y} \right)$). На рис. 2 для четвертой задачи показаны широтные профили проводимостей Холла и Педерсена и аналитическое решение при проводимостях Педерсена и Холла, изменяющихся по экспоненте от экватора к высоким широтам и постоянных по долготе. Также на этом рисунке показаны погрешности моделей 2 и 1. Видно, что точность модели 2 в 8–20 раз выше, чем модели 1. Максимальная погрешность модели 1 вблизи экватора составила 0.2 кВ, а в высоких широтах – 0.4 кВ, тогда как погрешность модели 2 там же составила 0.01 и 0.05 кВ соответственно. При этом время счета в 3 раза меньше для модели 2 по сравнению с моделью 1.

Пятая, наиболее общая задача подробно описана в разд. 2. Она отличается от предыдущих тем, что в ней учитывается область экваториальной электроструи с высокими значениями проводимости Каулинга ${{{{\Sigma }}}_{C}}.$ На рис. 3 для пятой задачи показаны широтные профили проводимостей Холла, Педерсена и Каулинга, фрагмент их высотных профилей на геомагнитном экваторе и аппроксимирующие их функции, позволяющие получить аналитическое решение. Следует отметить, что заданные высотные профили проводимостей близки к среднеклиматическим профилям, полученным с использованием справочной модели ионосферы IRI [36] и представленным на рис. 3. На этом же рисунке показаны распределения электрического потенциала и погрешности, полученные для этого случая в моделях 2 и 1. Различия аналитического и модельных распределений электрического потенциала для этого случая в высоких и средних широтах практически не видны. Вблизи экватора эти различия возрастают. Точность модели 2 в 3–5 раз выше, чем модели 1. Максимальная погрешность модели 1 вблизи экватора составила 0.1 кВ (~8%), а в высоких широтах – 0.15 кВ (~0.6%), тогда как погрешность модели 2 там же составила 0.015 кВ (~1.5%) и 0.05 кВ (~0.2%) соответственно. При этом время счета в 3 раза меньше для модели 2.

Поскольку слой экваториальных электроструй, соответствующий $0 < y < {{y}_{e}},$ соответствующий магнитным силовым линиям, вершины которых находятся в интервале высот 90–120 км, в тысячи раз тоньше, чем длина границы (40 000 км), его можно эффективно изучать как пограничный слой. Такая теория была разработана Ричмондом [37]. Соответствующее моделирование пограничного слоя со специальным граничным условием, заменяющим условие (7), было представлено в книге [33], включая постановку задачи с самосопряженным положительно определенным оператором и ее численную версию. При использовании такой модификации нашего численного метода время вычислений для анализируемого теста сокращается примерно в 7 раз, при этом погрешность остается прежней.

5. ЗАКЛЮЧЕНИЕ

В статье представлены результаты тестовых расчетов двух численных моделей потенциала электрического поля в ионосфере Земли. Погрешности моделей, полученные при решении различных задач, показали, что обе модели могут быть использованы для расчета электрического потенциала в моделях верхней атмосферы, в том числе в области экваториальной электроструи. Однако совместное использование метода конечных элементов и многосеточного метода Федоренко с предварительным переходом к задаче для специальных потенциалов приводит к значительно более точному и быстрому решению двумерного уравнения электропроводности в ионосфере, чем метод конечных разностей, используемый в блоке расчета электрического потенциала модели ГСМ ТИП.

Работа выполнена при финансовой поддержке грантом Российского научного фонда № 21-17-00208.