1. На главную
  2. Электронные версии
  3. Химическая физика
  4. T. 41, № 10, 2022

Химическая физика, 2022, T. 41, № 10, стр. 3-9

Релятивистский эффект Яна–Теллера 2Tg × eg в октаэдрических молекулах с тяжелым центральным атомом

В. М. Волохов 1, *, Л. В. Полуянов 1

1 Институт проблем химической физики Российской академии наук
Черноголовка, Россия

* E-mail: vvm@icp.ac.ru

Поступила в редакцию 09.11.2021
После доработки 16.12.2021
Принята к публикации 20.12.2021

Полный текст (PDF)

Аннотация

Анализ основан на учете спин-орбитального взаимодействия в форме оператора Брейта–Паули в электронном гамильтониане молекулы. В качестве последнего мы рассматриваем гамильтониан октаэдрической молекулы ${{\tilde {Y}}}{{{\text{X}}}_{6}}$ с нечетным числом электронов и тяжелым центральным атомом ${{\tilde {Y},}}$ находящимся в орбитальном 2D-состоянии с одним внешним электроном, и шестью атомами-лигандами X, образующими замкнутую электронную оболочку. Ключевым элементом анализа является построение симметризованных комбинаций произведений eg-мод и матриц Паули с последующим разложением электронного гамильтониана в ряд Тейлора по упомянутым симметризованным комбинациям. При этом были учтены вклады основного, первого и второго порядков по степеням eg-мод нормальных колебаний. Вибронная матрица 6 × 6, зависящая от двух eg-мод, была рассчитана в диабатическом электронном базисе, сконструированном из произведений компонент орбитального D-состояния и электронных спиновых функций. Вибронная матрица включает четыре электростатических параметра и четыре параметра спин-орбитального происхождения. Собственные значения вибронной матрицы (т.е. поверхности потенциальной энергии) инвариантны относительно операций группы молекулярной симметрии $O_{h}^{'}.$

Ключевые слова: электронный гамильтониан, оператор спин-орбитального взаимодействия, молекулярная группа симметрии, двойная группа симметрии, симметризованные комбинации, разложение электронного гамильтониана, ряд Тейлора, диабатический базис электронных состояний, групповые правила отбора, вибронная матрица, поверхности потенциальной энергии.

ВВЕДЕНИЕ

Комплексные (координационные) соединения широко распространены в живой и неживой природе, применяются в промышленности, сельском хозяйстве, науке, медицине. Способность веществ образовывать комплексные соединения используется для разработки эффективных методов получения химически чистых металлов из руд, редких металлов, сверхчистых полупроводниковых материалов, катализаторов, красителей, лекарственных препаратов, очистки природных и сточных вод, растворения накипи в парогенераторах и т.п.

Комплексные соединения [MeF6], где Me – тяжелый металл (возможно, ион), а F – атом фтора, часто встречаются как объект синтеза или составляющая технологического процесса. Поэтому исследование их физико-химических свойств как аналитическими, так и расчетными ab initio методами [1–4] представляет значительный интерес.

В данной работе мы рассматриваем релятивистский эффект Яна–Теллера 2Tg × eg в октаэдрических молекулах ${{\tilde {Y}}}{{{\text{X}}}_{{\text{6}}}}$ с тяжелым центральным атомом ${{\tilde {Y},}}$ находящимся в состоянии 2D, имеющим один внешний неспаренный d-электрон, при том что все остальные электронные оболочки (как в ${{\tilde {Y},}}$ так и в лигандном комплексе X6) являются замкнутыми. Примерами молекул такого типа могут служить Ti3+F6, Zr3+F6, Sc2+F6, Y2+F6 и др. [5–7].

В данной постановке физическая проблема является в основном одноэлектронной. Ниже мы упростим эту ситуацию и будем рассматривать модельную систему: один d-электрон центрального атома в октаэдрическом окружении шести равных электростатических зарядов. Неискаженная нормальными колебаниями октаэдрическая конфигурация рассматриваемой модели показана на рис. 1.

Рис. 1.

Октаэдрическая молекула ${{\tilde {Y}}}{{{\text{X}}}_{{\text{6}}}}$ во внешнем кубе. Центральный атом ${{\tilde {Y}}}$ находится в начале системы координат x, y, z.

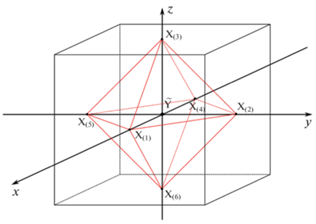
Семиатомная октаэдрическая молекула ${{\tilde {Y}}}{{{\text{X}}}_{{\text{6}}}}$ характеризуется совокупностью Ω пятнадцати мод нормальных колебаний11:

(1)
${{\Omega }} = \left\{ {{{a}_{{1g}}},~{{e}_{g}},~{{t}_{{2g}}},~2{{t}_{{1u}}},~{{t}_{{2u}}}} \right\}.$

В данной работе мы считаем, что из всего множества (1) активирована только пара eg-мод нормальных колебаний.

Геометрической группой симметрии молекулы ${{\tilde {Y}}}{{{\text{X}}}_{{\text{6}}}}$ является группа $~{{O}_{h}}$. Некоторые неприводимые представления этой группы характеризуют симметрию нормальных колебаний в (1). Для проектирования eg-мод из межатомных расстояний условимся обозначать через $\left| {{{\tilde {Y}}}{{{\text{X}}}_{{\left( k \right)}}}} \right|$ расстояние от атома-лиганда X(k) до центрального атома 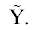Пользуясь результатами работы [6], мы можем представить координаты eg-мод в следующей форме:

(2)
$\left\{ {\begin{array}{*{20}{l}} \begin{gathered} u = \frac{1}{{2\sqrt 3 }}\left( {2\left| {{{\tilde {Y}}}{{{\text{X}}}_{{\left( 3 \right)}}}} \right| + 2\left| {{{\tilde {Y}}}{{{\text{X}}}_{{\left( 6 \right)}}}} \right| - \left| {{{\tilde {Y}}}{{{\text{X}}}_{{\left( 1 \right)}}}} \right| - } \right. \hfill \\ - \,\,\left. {\left| {{{\tilde {Y}}}{{{\text{X}}}_{{\left( 4 \right)}}}} \right| - \left| {{{\tilde {Y}}}{{{\text{X}}}_{{\left( 2 \right)}}}} \right| - \left| {{{\tilde {Y}}}{{{\text{X}}}_{{\left( 5 \right)}}}} \right|} \right), \hfill \\ \end{gathered} \\ {v = \frac{1}{2}\left( {\left| {{{\tilde {Y}}}{{{\text{X}}}_{{\left( 1 \right)}}}} \right| + \left| {{{\tilde {Y}}}{{{\text{X}}}_{{\left( 4 \right)}}}} \right| - \left| {{{\tilde {Y}}}{{{\text{X}}}_{{\left( 2 \right)}}}} \right| - \left| {{{\tilde {Y}}}{{{\text{X}}}_{{\left( 5 \right)}}}} \right|} \right).} \end{array}} \right.$

Инвариантность eg-мод u и v относительно операции инверсии (т.е. их четность) очевидна: как следует из рис. 1, при инверсии в выражениях (2) меняются местами только слагаемые с одинаковыми знаками.

Полученная в этой работе вибронная матрица 6 × 6 может быть применена для расчета или интерпретации фотоэлектронных спектров октаэдрических молекул (с тяжелым центральным атомом) в спиновом состоянии S = 1/2. Для этого наш анализ должен быть дополнен расчетом упомянутых выше восьми постоянных параметров для реальных исследуемых молекул с нечетным числом электронов в спиновом состоянии S = 1/2. Рассмотренная в данной работе одноэлектронная модель, разумеется, неприменима для этой цели. Расчет постоянных параметров требует полноформатного применения релятивистской квантовой химии с вычислением ab initio точек потенциальных поверхностей. Эта модель оставляет параметры неопределенными, но позволяет найти зависимость вибронной матрицы от колебательных мод, так как эта зависимость определяется только свойствами симметрии электронного гамильтониана, симметрией нормальных мод и квантовыми числами исследуемых электронных состояний.

ОДНОЭЛЕКТРОННЫЙ ГАМИЛЬТОНИАН И ЕГО СВОЙСТВА СИММЕТРИИ

Мы рассматриваем одноэлектронный гамильтониан, в котором центральный атом с электроном в d-состоянии находится в окружении шести одинаковых электростатических зарядов, расположенных в вершинах октаэдра:

(3)
$\hat {H} = {{\hat {H}}_{{es}}} + {{\hat {H}}_{{so}}},$
где
(4)
${{\hat {H}}_{{es}}} = - \frac{{{{\hbar }^{2}}}}{{2{{m}_{e}}}}{{\nabla }^{2}} - eQ{{\Phi }}\left( r \right) - \frac{{e{{Q}_{0}}}}{{{{r}_{0}}}}$
– электростатическая часть гамильтониана,
(5)
${{\hat {H}}_{{so}}} = ig\beta _{e}^{2}S\left[ {\nabla \left( {Q{{\Phi }} + \frac{{{{Q}_{0}}}}{{{{r}_{0}}}}} \right)\nabla } \right]$
– оператор спин-орбитального взаимодействия Брейта–Паули [8].

В формулах (4), (5) использованы следующие обозначения:

(6)
${{\Phi }}\left( r \right) = \sum\limits_{k = 1}^6 {\frac{1}{{\left| {r - {{R}_{k}}} \right|}}} ;$
r – радиус-вектор электрона; Rk – радиус-векторы атомов-лигандов; ${{r}_{0}} = \left| {r - {{R}_{0}}} \right|,~\,{{R}_{0}}$ – радиус-вектор центрального атома (который может быть смещён из центра октаэдра); ${{\beta }_{e}} = {{e\hbar } \mathord{\left/ {\vphantom {{e\hbar } {2{{m}_{e}}c}}} \right. \kern-0em} {2{{m}_{e}}c}}$ – магнетон Бора [8]; $g = 2.0023$ – g-фактор свободного электрона; $S = \frac{1}{2}\left( {{{{\hat {\sigma }}}_{x}},{{{\hat {\sigma }}}_{y}},{{{\hat {\sigma }}}_{z}}} \right)$ – вектор операторов электронного спина, ${{\hat {\sigma }}_{x}},{{\hat {\sigma }}_{y}},{{\hat {\sigma }}_{z}}$ – матрицы Паули; ${{Q}_{0}}$ – заряд центрального ядра; $Q$ – заряд ядер-лигандов.

Операции геометрической группы симметрии ${{O}_{h}}$ не коммутируют с гамильтонианом (3) из-за наличия спин-орбитального взаимодействия ${{\hat {H}}_{{so}}}.$ Модельный одноэлектронный гамильтониан, представленный соотношениями (3)–(6), характеризуется двойной группой симметрии $O_{h}^{'}$ (в силу нечетного числа электронов в системе). Упомянутая двойная группа $O_{h}^{'}$ имеет 16 неприводимых представлений. Десять из них являются однозначными –

$\frac{{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{A}_{{1g}}},}&{{{A}_{{2g}}},}&{{{E}_{g}},} \end{array}}&{\begin{array}{*{20}{c}} {{{T}_{{1g}}},}&{{{T}_{{2g}}};} \end{array}} \end{array}}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{A}_{{1u}}},}&{{{A}_{{2u}}},} \end{array}}&{\begin{array}{*{20}{c}} {{{E}_{u}},}&{{{T}_{{1u}}},}&{{{T}_{{2u}}}} \end{array}} \end{array}} \end{array}}}{{~~\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {1~~~}&{~~1~~~}&{~~2~~~} \end{array}}&{~~\begin{array}{*{20}{c}} {3~~~}&{~~3~~~} \end{array}} \end{array}}&{~~\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {1~~~}&{~~1~~~} \end{array}}&{\begin{array}{*{20}{c}} {~~2~~~}&{~~3~~~}&{~~3~~~} \end{array}} \end{array}} \end{array}}},$
и еще шесть неприводимых представлений являются двузначными –

$\frac{{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{E}_{g}}\left( {\frac{1}{2}} \right),}&{{{E}_{g}}\left( {\frac{5}{2}} \right),}&{{{G}_{g}}\left( {\frac{3}{2}} \right);} \end{array}}&{\begin{array}{*{20}{c}} {{{E}_{u}}\left( {\frac{1}{2}} \right),}&{{{E}_{u}}\left( {\frac{5}{2}} \right),}&{{{G}_{u}}\left( {\frac{3}{2}} \right)} \end{array}} \end{array}}}{{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {~~\,\,2~~~}&{~~~~~\,\,2~}&{~~~~\,\,~~4~~} \end{array}}&{\begin{array}{*{20}{c}} {~~~~\,\,~~2~~~~}&{~~~~~~2~~~~}&{~~~~\,\,\,~4~~} \end{array}} \end{array}}}.$

Цифры под обозначениями неприводимых представлений указывают их размерности. Двойная группа симметрии $O_{h}^{'}$ включает 96 операторов, коммутирующих с гамильтонианом (3)–6). Методы вычисления этих операторов симметрии подробно изложены в работах [6, 9, 10]. Опуская детали расчета этих операторов, мы приводим их полный набор в Приложении. Характерной чертой операторов $O_{h}^{'}$ является их мультипликативная структура: каждый из операторов (кроме единицы и инверсии) представляет собой произведение унитарной матрицы (действующей на компоненты электронного спина) на пространственную операцию (действующую на координаты электрона).

Помимо операторов симметрии, составляющих группу $O_{h}^{'},$ одноэлектронный гамильтониан (3)–(6) коммутирует с антиунитарным оператором обращения времени [11, 12]:

(7)
$\hat {T} = \left( {\begin{array}{*{20}{c}} 0&{ - 1} \\ 1&0 \end{array}} \right)\widehat {{\text{c}}{\text{.c}}{\text{.}}},\,\,\,\,{{\hat {T}}^{2}} = - 1,$
где оператор $\widehat {{\text{c}}{\text{.c}}{\text{.}}}$ обозначает комплексное сопряжение.

Оператор симметрии $\hat {T}$ коммутирует с операторами из двойной группы $O_{h}^{'}.$ Полная группа симметрии является прямым произведением:

(8)
$G = O_{h}^{'} \times \left( {\hat {E},\hat {T}} \right),$
где – E – единичный оператор, и включает в себя 192 элемента.

РАЗЛОЖЕНИЕ ОДНОЭЛЕКТРОННОГО ГАМИЛЬТОНИАНА В РЯД ТЕЙЛОРА

Мы считаем, что нормальные колебания являются относительно малыми по сравнению с межъядерными расстояниями в симметричной молекуле и не искажают существенно ее симметричную конфигурацию. По этой причине электронный гамильтониан (3)–(6) мы разлагаем в ряд Тейлора по eg-модам u и v с удержанием членов основного, первого и второго порядков.

Наиболее очевидным является разложение электронного гамильтониана по степеням и произведениям u и v и по произведениям u и v на матрицы Паули. Однако этот метод имеет тот очевидный недостаток, что упомянутые выше степени и произведения не обладают должной симметрией и не принадлежат неприводимым представлениям молекулярной группы симметрии. Имея в виду применение в дальнейшем групповых правил отбора при вычислении матричного представления электронного гамильтониана, мы будем ниже использовать для разложения в ряд Тейлора такие симметризованные комбинации произведений u, v и матриц Паули, которые принадлежат неприводимым представлениям группы молекулярной симметрии. Все упомянутые выше симметризованные комбинации приведены в табл. 1.

Таблица 1.  

Симметризованные комбинации произведений нормальных мод и матриц Паули

Порядок Номера симметризованных комбинаций Симметрия Симметризованные комбинации
Нулевой спин-орбитальный 1, 2, 3 ${{t}_{{1g}}}$ ${{\hat {\sigma }}_{x}},~{{\hat {\sigma }}_{y}},~{{\hat {\sigma }}_{z}}$
Первый орбитальный 4, 5 ${{e}_{g}}$ u, v
Первый спин-орбитальный 6, 7, 8 ${{t}_{{1g}}}$ ${{\hat {y}}_{1}} = {{w}^{ - }}{{\hat {\sigma }}_{x}}$, ${{\hat {y}}_{2}} = {{w}^{ + }}{{\hat {\sigma }}_{y}}$, ${{\hat {y}}_{3}} = - u{{\hat {\sigma }}_{z}}$
9, 10, 11 ${{t}_{{2g}}}$ ${{\hat {x}}_{1}} = - {{w}_{ + }}{{\hat {\sigma }}_{x}}$, ${{\hat {x}}_{2}} = {{w}_{ - }}{{\hat {\sigma }}_{y}}$, ${{\hat {x}}_{3}} = v{{\hat {\sigma }}_{z}}$
Второй орбитальный 12 ${{a}_{{1g}}}$ $I_{2}^{{ee}} = \frac{1}{{\sqrt 2 }}\left( {{{u}^{2}} + {{v}^{2}}} \right)$
13, 14 ${{e}_{g}}$ ${{Z}_{1}} = \frac{1}{{\sqrt 2 }}\left( {{{u}^{2}} - {{v}^{2}}} \right)$
${{Z}_{2}} = - \sqrt 2 uv$
Второй спин-орбитальный 15, 16, 17 ${{t}_{{1g}}}$ $\hat {Y}_{1}^{{\left( 1 \right)}} = I_{2}^{{ee}}{{\hat {\sigma }}_{x}}$, $\hat {Y}_{2}^{{\left( 1 \right)}} = I_{2}^{{ee}}{{\hat {\sigma }}_{y}}$, $\hat {Y}_{3}^{{\left( 1 \right)}} = I_{2}^{{ee}}{{\hat {\sigma }}_{z}}$
18, 19, 20 ${{t}_{{1g}}}$ $\hat {Y}_{1}^{{\left( 2 \right)}} = {{Z}^{ - }}{{\hat {\sigma }}_{x}}$, $\hat {Y}_{2}^{{\left( 2 \right)}} = {{Z}^{ + }}{{\hat {\sigma }}_{y}}$, $\hat {Y}_{3}^{{\left( 2 \right)}} = - {{Z}_{1}}{{\hat {\sigma }}_{z}}$
21, 22, 23 ${{t}_{{2g}}}$ ${{\hat {X}}_{1}} = - {{Z}_{ + }}{{\hat {\sigma }}_{x}}$, ${{\hat {X}}_{2}} = {{Z}_{ - }}{{\hat {\sigma }}_{y}}$, ${{\hat {X}}_{3}} = {{Z}_{2}}{{\hat {\sigma }}_{z}}$

Примечания: ${{Z}_{ \pm }} = \frac{{\sqrt 3 }}{2}{{Z}_{1}} \pm \frac{1}{2}{{Z}_{2}},$ ${{Z}^{ \pm }} = \frac{1}{2}{{Z}_{1}} \pm \frac{{\sqrt 3 }}{2}{{Z}_{2}},$ ${{w}_{ \pm }} = \frac{{\sqrt 3 }}{2}u \pm \frac{1}{2}~v,$ ${{w}^{ \pm }} = \frac{1}{2}u \pm \frac{{\sqrt 3 }}{2}~v.$

Стоит подчеркнуть, что число симметризованных комбинаций в точности равно числу учтенных степеней нормальных мод и их произведений друг на друга и на матрицы Паули. В данной работе число используемых симметризованных комбинаций равно 23. Ряды Тейлора для электронного гамильтониана мы записываем раздельно для ${{\hat {H}}_{{es}}}$ и ${{\hat {H}}_{{so}}}{\text{:}}$

(9)
${{\hat {H}}_{{es}}} = {{\hat {H}}_{0}}\left( {{{T}_{{2g}}}} \right) + {{\hat {H}}_{1}} + {{\hat {H}}_{2}} + \ldots ,$
(10)
${{\hat {H}}_{{so}}} = {{\hat {h}}_{0}} + {{\hat {h}}_{1}} + {{\hat {h}}_{2}} + \ldots $
где ${{\hat {H}}_{k}}$ и ${{\hat {h}}_{k}}$ включают в себя только члены k-го порядка по степеням нормальных мод (k = 0, 1, 2). Ниже мы приводим более подробную форму операторов ${{\hat {H}}_{k}}$ и ${{\hat {h}}_{k}}{\text{:}}$

${{\hat {H}}_{0}}\left( {{{T}_{{2g}}}} \right)$ – собственное значение оператора (4) на собственной функции симметрии ${{T}_{{2g}}},$

(11)
${{\hat {H}}_{1}} = {{\hat {H}}^{{\left( 1 \right)}}}~\left( {{{e}_{g}}} \right)u + {{\hat {H}}^{{\left( 2 \right)}}}~\left( {{{e}_{g}}} \right)v,$
(12)
${{\hat {H}}_{2}} = \hat {H}\left( {{{a}_{{1g}}}} \right)I_{2}^{{ee}} + \,{{\,}_{1}}\hat {H}\left( {{{e}_{g}}} \right){{Z}_{1}} + \,{{\,}_{2}}\hat {H}\left( {{{e}_{g}}} \right){{Z}_{2}}.$
Ряды Тейлора для оператора ${{\hat {H}}_{{so}}}$ имеют следующий вид:

(13)
${{\hat {h}}_{0}} = {{\hat {h}}_{1}}\left( {{{t}_{{1g}}}} \right){{\hat {\sigma }}_{x}} + {{\hat {h}}_{2}}\left( {{{t}_{{1g}}}} \right){{\hat {\sigma }}_{y}} + {{\hat {h}}_{3}}\left( {{{t}_{{1g}}}} \right){{\hat {\sigma }}_{z}},$
(14)
$\begin{gathered} {{{\hat {h}}}_{1}} = \hat {h}_{1}^{{\left( 1 \right)}}\left( {{{t}_{{1g}}}} \right){{{\hat {y}}}_{1}} + \hat {h}_{2}^{{\left( 1 \right)}}\left( {{{t}_{{1g}}}} \right){{{\hat {y}}}_{2}} + \hat {h}_{3}^{{\left( 1 \right)}}\left( {{{t}_{{1g}}}} \right){{{\hat {y}}}_{3}} + \\ + \,\,\hat {h}_{1}^{{\left( 2 \right)}}\left( {{{t}_{{2g}}}} \right){{{\hat {x}}}_{1}} + \hat {h}_{2}^{{\left( 2 \right)}}\left( {{{t}_{{2g}}}} \right){{{\hat {x}}}_{2}} + \hat {h}_{3}^{{\left( 2 \right)}}\left( {{{t}_{{2g}}}} \right){{{\hat {x}}}_{3}}, \\ \end{gathered} $
(15)
$\begin{gathered} {{{\hat {h}}}_{2}} = \hat {h}_{1}^{{\left( 3 \right)}}\left( {{{t}_{{1g}}}} \right)\hat {Y}_{1}^{{\left( 1 \right)}} + \hat {h}_{2}^{{\left( 3 \right)}}\left( {{{t}_{{1g}}}} \right)\hat {Y}_{2}^{{\left( 1 \right)}} + \hat {h}_{3}^{{\left( 3 \right)}}\left( {{{t}_{{1g}}}} \right)\hat {Y}_{3}^{{\left( 1 \right)}} + \\ + \,\,\hat {h}_{1}^{{\left( 4 \right)}}\left( {{{t}_{{1g}}}} \right)\hat {Y}_{1}^{{\left( 2 \right)}} + \hat {h}_{2}^{{\left( 4 \right)}}\left( {{{t}_{{1g}}}} \right)\hat {Y}_{2}^{{\left( 2 \right)}} + \hat {h}_{3}^{{\left( 4 \right)}}\left( {{{t}_{{1g}}}} \right)\hat {Y}_{3}^{{\left( 2 \right)}} + \\ + \,\,\hat {h}_{1}^{{\left( 5 \right)}}\left( {{{t}_{{2g}}}} \right){{{\hat {X}}}_{1}} + \hat {h}_{2}^{{\left( 5 \right)}}\left( {{{t}_{{2g}}}} \right){{{\hat {X}}}_{2}} + \hat {h}_{3}^{{\left( 5 \right)}}\left( {{{t}_{{2g}}}} \right){{{\hat {X}}}_{3}}. \\ \end{gathered} $

В рядах Тейлора (11)–15) использованы симметризованные комбинации (${{\hat {y}}_{{1,2,3}}};$ ${{\hat {x}}_{{1,2,3}}};$ $I_{2}^{{ee}};$ ${{Z}_{{1,2}}};$ $\hat {Y}_{{1,2,3}}^{{\left( {1,2} \right)}};$ ${{\hat {X}}_{{1,2,3}}}$), представленные в табл. 1. Коэффициенты рядов $_{ \ldots }\hat {H},$ ${{\hat {H}}^{ \ldots }}$и $\hat {h}_{ \ldots }^{ \ldots }$ обладают определенной симметрией в группе $O_{h}^{'}.$ В частности, они преобразуются в $O_{h}^{'}$ по однозначным неприводимым представлениям, которые указаны в круглых скобках как аргументы этих коэффициентов. Данная конструкция симметризованных комбинаций и соответствующих им симметричных коэффициентов обеспечивает инвариантность в группе $O_{h}^{'}$ каждой строчки в рядах Тейлора (11)–(15).

МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ЭЛЕКТРОННОГО ГАМИЛЬТОНИАНА

Как уже отмечалось выше, мы считаем, что центральный атом ${{\tilde {Y}}}$ имеет один неспаренный внешний электрон, который находится в d-состоянии и окружен шестью равными электростатическими зарядами в вершинах октаэдра. В этом случае пятикратно вырожденное d-состояние расщепляется на трехкратно вырожденное состояние T2g-симметрии –

(16)
$\left. {\begin{array}{*{20}{c}} {X = yz~D\left( r \right)} \\ {Y = xz~D\left( r \right)} \\ {Z = xy~D\left( r \right)} \end{array}} \right\}$
и на двукратно вырожденное состояние Eg-симметрии –

(17)
$\left. {\begin{array}{*{20}{l}} {U = \frac{1}{{\sqrt 6 }}\left( {2{{z}^{2}} - {{x}^{2}} - {{y}^{2}}} \right)D\left( r \right)} \\ {V = \frac{1}{{\sqrt 2 }}\left( {{{x}^{2}} - {{y}^{2}}} \right)D\left( r \right)} \end{array}} \right\}.$

В выражениях (16) и (17) множитель D(r) является изотропным. Все атомные орбитали (16), (17) подразумеваются нормированными. Поскольку мы исследуем здесь релятивистский эффект Яна–Теллера $~{{T}_{{2g}}} \times {{e}_{g}},$ нас будут интересовать только орбитальные состояния (16). Для матричного представления электронного гамильтониана мы вводим базис шести спин-орбиталей:

(18)
${{\tilde {\Omega }}} = \left\{ {X\alpha ,~Y\alpha ,~Z\alpha ,~Z\beta ,Y\beta ,~X\beta } \right\}.$

Принимая во внимание, что спиновые функции

(19)
$\alpha = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)\,\,{\text{и}}\,\,\beta = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)$
принадлежат двузначному неприводимому представлению Eg(1/2) [13], мы находим, что набор шести спин-орбиталей (18) образует двузначное приводимое представление группы $O_{h}^{'},$ которое может быть разложено в следующую сумму неприводимых представлений [13]:

(20)
${{T}_{{2g}}} \times {{E}_{g}}\left( {\frac{1}{2}} \right) = {{E}_{g}}\left( {\frac{5}{2}} \right) + {{G}_{g}}\left( {\frac{3}{2}} \right).$

Ниже мы используем базис (18) и разложение на фрагменты (3), (9)–15) для электростатической и спин-орбитальной частей электронного гамильтониана с целью расчета матричных элементов. Проводя эти вычисления, мы вначале осуществляем интегрирование по спиновым переменным. Те матричные элементы, которые при этом не обнуляются, анализируются далее на основе групповых правил отбора. Следует подчеркнуть, что орбитальные части базисных функций (18) преобразуются по однозначному неприводимому представлению T2g, а все коэффициенты рядов Тейлора (11)–15) преобразуются по различным, но тоже однозначным неприводимым представлениям группы $O_{h}^{'}.$ Наличие этой симметрии у множителей интеграндов (матричных элементов) существенно облегчает нахождение отличных от нуля матричных элементов и возможных связей между ними. Дополнительные ограничения на константы вибронного взаимодействия накладывает требование коммутации вибронной матрицы с оператором обращения времени (7), который в базисе (18) приобретает следующий вид:

(21)
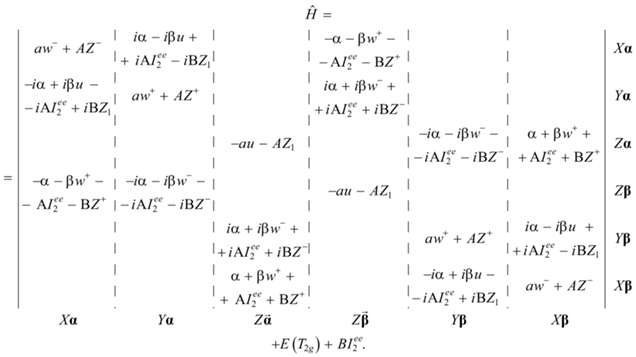
$\hat {T} = \left| {\begin{array}{*{20}{c}} {}&{}&{}&{}&{}&1 \\ {}&{}&{}&{}&1&{} \\ {}&{}&{}&1&{}&{} \\ {}&{}&{ - 1}&{}&{}&{} \\ {}&{ - 1}&{}&{}&{}&{} \\ { - 1}&{}&{}&{}&{}&{} \end{array}} \right|~\widehat {{\text{c}}{\text{.c}}{\text{.}}}$

Опуская детали вычислений, приводим ниже результирующее матричное представление электронного гамильтониана, т.е. вибронную матрицу 6 × 6, зависящую от двух вырожденных нормальных мод, u и v:

(22)

В вибронной матрице (22) латинскими буквами a, A, B, E обозначены электростатические параметры, греческими буквами α, β, A, B – параметры, имеющие спин-орбитальное происхождение.

Комбинации нормальных мод $\left( {{{w}^{ \pm }},~{{Z}_{1}},{{Z}^{ \pm }},~I_{2}^{{ee}}} \right)$ определены в табл. 1 (симметризованные комбинации).

ЗАКЛЮЧЕНИЕ

Расчет вибронной матрицы (22) является основным результатом данной работы. Шесть собственных векторов и собственных ее значений представляют собой три дублета Крамерса [11, 12]. В силу этого число различных собственных значений равно трем (каждое двукратно вырождено из-за нечетного числа электронов и симметрии вибронной матрицы по отношению к обращению времени).

Если мы перейдем от базиса (18) к новому электронному базису, две функции которого преобразуются по двузначному неприводимому представлению Eg(5/2) и четыре – по двузначному неприводимому представлению Gg(3/2), то в силу соотношения (20) для неприводимых представлений становится очевидно, что вибронная матрица (22) описывает релятивистский псевдо-эффект Яна–Теллера $\left[ {{{E}_{g}}\left( {5{\text{/}}2} \right) + {{G}_{g}}\left( {3{\text{/}}2} \right)} \right] \times {{e}_{g}}.$ Собственные значения вибронной матрицы (22) имеют чрезвычайно громоздкий вид и могут быть исследованы численно для конкретного набора параметров, рассчитанных для исследуемой молекулы.

ПРИЛОЖЕНИЕ

Операторы двойной группы молекулярнойметрии $O_{h}^{'}$

1. $\hat {E}$ – единичный оператор 25. $\hat {I}$ – инверсия
2. $\hat {Z}_{2}^{x} = i\hat {\mathbb{C}}_{2}^{x}\left( {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right)$ 26. $\hat {\mathbb{Z}}_{2}^{x} = \hat {I}\hat {Z}_{2}^{x}$
3. $\hat {Z}_{2}^{y} = i\hat {\mathbb{C}}_{2}^{y}\left( {\begin{array}{*{20}{c}} 0&{ - i} \\ i&0 \end{array}} \right)$ 27. $\hat {\mathbb{Z}}_{2}^{y} = \hat {I}\hat {Z}_{2}^{y}$
4. $\hat {Z}_{2}^{z} = i\hat {\mathbb{C}}_{2}^{z}\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{ - 1} \end{array}} \right)$ 28. $\hat {\mathbb{Z}}_{2}^{z} = \hat {I}\hat {Z}_{2}^{z}$
5. ${{\hat {Z}}_{{3ah}}} = {{e}^{ - }}{{\hat {C}}_{{3ah}}}\left( {\begin{array}{*{20}{c}} \nu &{ - i\nu } \\ \nu &{i\nu } \end{array}} \right)$ 29. ${{\hat {\mathbb{Z}}}_{{3ah}}} = \hat {I}{{\hat {Z}}_{{3ah}}}$
6. ${{\hat {Z}}_{{3bg}}} = {{e}^{ - }}{{\hat {C}}_{{3bg}}}\left( {\begin{array}{*{20}{c}} \nu &{ - \nu } \\ {i\nu }&{i\nu } \end{array}} \right)$ 30. ${{\hat {\mathbb{Z}}}_{{3bg}}} = \hat {I}{{\hat {Z}}_{{3bg}}}$
7. ${{\hat {Z}}_{{3cf}}} = {{e}^{ + }}{{\hat {C}}_{{3cf}}}\left( {\begin{array}{*{20}{c}} \nu &{i\nu } \\ \nu &{ - i\nu } \end{array}} \right)$ 31. ${{\hat {\mathbb{Z}}}_{{3cf}}} = \hat {I}{{\hat {Z}}_{{3cf}}}$
8. ${{\hat {Z}}_{{3de}}} = {{e}^{ + }}{{\hat {C}}_{{3de}}}\left( {\begin{array}{*{20}{c}} \nu &{ - \nu } \\ { - i\nu }&{ - i\nu } \end{array}} \right)$ 32. ${{\hat {\mathbb{Z}}}_{{3de}}} = \hat {I}{{\hat {Z}}_{{3de}}}$
9. $\hat {Z}_{{3ah}}^{2} = - {{e}^{ + }}\hat {C}_{{3ah}}^{2}\left( {\begin{array}{*{20}{c}} \nu &\nu \\ {i\nu }&{ - i\nu } \end{array}} \right)$ 33. $\hat {\mathbb{Z}}_{{3ah}}^{{\left( 2 \right)}} = \hat {I}\hat {Z}_{{3ah}}^{2}$
10. $\hat {Z}_{{3bg}}^{2} = - {{e}^{ + }}\hat {C}_{{3bg}}^{2}\left( {\begin{array}{*{20}{c}} \nu &{ - i\nu } \\ { - \nu }&{ - i\nu } \end{array}} \right)$ 34. $\hat {\mathbb{Z}}_{{3bg}}^{{\left( 2 \right)}} = \hat {I}\hat {Z}_{{3bg}}^{2}$
11. $\hat {Z}_{{3cf}}^{2} = - {{e}^{ - }}\hat {C}_{{3cf}}^{2}\left( {\begin{array}{*{20}{c}} \nu &\nu \\ { - i\nu }&{i\nu } \end{array}} \right)$ 35. $\hat {\mathbb{Z}}_{{3cf}}^{{\left( 2 \right)}} = \hat {I}\hat {Z}_{{3cf}}^{2}$
12. $\hat {Z}_{{3de}}^{2} = - {{e}^{ - }}\hat {C}_{{3de}}^{2}\left( {\begin{array}{*{20}{c}} \nu &{i\nu } \\ { - \nu }&{i\nu } \end{array}} \right)$ 36. $\hat {\mathbb{Z}}_{{3de}}^{{\left( 2 \right)}} = \hat {I}\hat {Z}_{{3de}}^{2}$
13. $\hat {Z}_{{2ab}}^{{gh}} = \hat {C}_{{2ab}}^{{gh}}\left( {\begin{array}{*{20}{c}} { - i\nu }&{ - \nu } \\ \nu &{i\nu } \end{array}} \right)$ 37. $\hat {\mathbb{Z}}_{{3ab}}^{{gh}} = \hat {I}\hat {Z}_{{3ab}}^{{gh}}$
14. $\hat {Z}_{{2dc}}^{{ef}} = \hat {C}_{{2dc}}^{{ef}}\left( {\begin{array}{*{20}{c}} { - i\nu }&\nu \\ { - \nu }&{i\nu } \end{array}} \right)$ 38. $\hat {\mathbb{Z}}_{{3dc}}^{{ef}} = \hat {I}\hat {Z}_{{3dc}}^{{ef}}$
15. $\hat {Z}_{{2bc}}^{{gf}} = \hat {C}_{{2bc}}^{{gf}}\left( {\begin{array}{*{20}{c}} 0&{ - {{e}^{ - }}} \\ {{{e}^{ + }}}&0 \end{array}} \right)$ 39. $\hat {\mathbb{Z}}_{{3bc}}^{{gf}} = \hat {I}\hat {Z}_{{3bc}}^{{gf}}$
16. $\hat {Z}_{{2ad}}^{{eh}} = \hat {C}_{{2ad}}^{{eh}}\left( {\begin{array}{*{20}{c}} 0&{{{e}^{ + }}} \\ { - {{e}^{ - }}}&0 \end{array}} \right)$ 40. $\hat {\mathbb{Z}}_{{3ad}}^{{eh}} = \hat {I}\hat {Z}_{{3ad}}^{{eh}}$
17. $\hat {Z}_{{2af}}^{{ch}} = \hat {C}_{{2af}}^{{ch}}\left( {\begin{array}{*{20}{c}} {i\nu }&{i\nu } \\ {i\nu }&{ - i\nu } \end{array}} \right)$ 41. $\hat {\mathbb{Z}}_{{3af}}^{{ch}} = \hat {I}\hat {Z}_{{3af}}^{{ch}}$
18. $\hat {Z}_{{2be}}^{{dg}} = \hat {C}_{{2be}}^{{dg}}\left( {\begin{array}{*{20}{c}} {i\nu }&{ - \nu } \\ { - i\nu }&{ - i\nu } \end{array}} \right)$ 42. $\hat {\mathbb{Z}}_{{3be}}^{{dg}} = \hat {I}\hat {Z}_{{3be}}^{{dg}}$
19. $\hat {Z}_{4}^{x} = \hat {C}_{4}^{x}\left( {\begin{array}{*{20}{c}} \nu &{ - i\nu } \\ { - i\nu }&\nu \end{array}} \right)$ 43. $\hat {\mathbb{Z}}_{4}^{x} = \hat {I}\hat {Z}_{4}^{x}$
20. $\hat {Z}_{4}^{y} = \hat {C}_{4}^{y}\left( {\begin{array}{*{20}{c}} \nu &{ - \nu } \\ \nu &\nu \end{array}} \right)$ 44. $\hat {\mathbb{Z}}_{4}^{y} = \hat {I}\hat {Z}_{4}^{y}$
21. $\hat {Z}_{4}^{z} = \hat {C}_{4}^{z}\left( {\begin{array}{*{20}{c}} {{{e}^{ - }}}&0 \\ 0&{{{e}^{ + }}} \end{array}} \right)$ 45. $\hat {\mathbb{Z}}_{4}^{z} = \hat {I}\hat {Z}_{4}^{z}$
22. $\hat {Z}_{4}^{{{{x}^{3}}}} = \hat {C}_{4}^{{{{x}^{3}}}}\left( {\begin{array}{*{20}{c}} \nu &{i\nu } \\ {i\nu }&\nu \end{array}} \right)$ 46. $\hat {\mathbb{Z}}_{4}^{{{{x}^{3}}}} = \hat {I}\hat {Z}_{4}^{{{{x}^{3}}}}$
23. $\hat {Z}_{4}^{{{{y}^{3}}}} = \hat {C}_{4}^{{{{y}^{3}}}}\left( {\begin{array}{*{20}{c}} \nu &\nu \\ { - \nu }&\nu \end{array}} \right)$ 47. $\hat {\mathbb{Z}}_{4}^{{{{y}^{3}}}} = \hat {I}\hat {Z}_{4}^{{{{y}^{3}}}}$
24. $\hat {Z}_{4}^{{{{z}^{3}}}} = \hat {C}_{4}^{{{{z}^{3}}}}\left( {\begin{array}{*{20}{c}} {{{e}^{ + }}}&0 \\ 0&{{{e}^{ - }}} \end{array}} \right)$ 48. $\hat {\mathbb{Z}}_{4}^{{{{z}^{3}}}} = \hat {I}\hat {Z}_{4}^{{{{z}^{3}}}}$
49.– 96. $\left( { - 1} \right) \times \left( {1. - 48.} \right): - E, - \hat {Z}_{2}^{x},~ \ldots , - \hat {\mathbb{Z}}_{4}^{{{{y}^{3}}}},\hat {\mathbb{Z}}_{4}^{{{{z}^{3}}}}$
Используемые обозначения: ${{e}^{ \pm }} = \exp \left( {{{ \pm i\pi } \mathord{\left/ {\vphantom {{ \pm i\pi } 4}} \right. \kern-0em} 4}} \right);$$\nu = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}.$ Обозначения пространственных операторов взяты из монографии [13].

Работа выполнена в соответствии с госзаданием (регистрационный номер АААА-А19-119071190017-7 (Л.В. Полуянов) и АААА-А19-119120690042-9 (В.М. Волохов)).

Список литературы

  1. Волохов В.М., Полуянов Л.В. // Хим. физика. 2020. Т. 39. № 3. С. 11.

  2. Волохов В.М., Полуянов Л.В. // Хим. физика. 2020. Т. 39. № 7. С. 21.

  3. Волохов В.М., Полуянов Л.В. // Хим. физика. 2021. Т. 40. № 3. С. 41.

  4. Полуянов Л.В., Ушаков В.Г. // Хим. физика. 2021. Т. 40. № 5. С. 3.

  5. Герцберг Г. Электронные спектры и строение многоатомных молекул. М.: Мир, 1969.

  6. Poluyanov L.V., Domcke W. // J. Chem. Phys. 2012. V. 137. P. 114101.

  7. Grinberg M., Mandelis A., Fjeldsted K. // Phys. Rev. B. 1993. V. 48. P. 5922.

  8. Банкер Ф. Симметрия молекул и молекулярная спектроскопия. М.: Мир, 1981.

  9. Poluyanov L.V., Domcke W. // Springer Ser. Chem. Phys. 2009. V. 97. P. 77.

  10. Poluyanov L.V., Domcke W. // Adv. Ser. Phys. Chem. 2011. V. 17. P. 117.

  11. Ландау Л.Д., Лифшиц Е.М. Квантовая механика. М.: Наука, 1974.

  12. Вигнер Е. Теория групп. М.: Изд-во иностр. лит., 1961.

  13. Balasubramanian K. Relativistic effects in chemistry. Part A: Theory and Techniques. N.Y. – Toronto: John Wiley and Sons, Inc., 1991.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Химическая физика

Архивы выпусков Информация о журнале Отправить рукопись в журнал