Химическая физика, 2022, T. 41, № 5, стр. 171-21
Флуктуационные особенности диффузного прохождения частицами узких каналов с препятствиями
А. Ф. Валов 1, *, В. А. Аветисов 1
1 Федеральный исследовательский центр химической физики им. Н.Н. Семёнова
Российской академии наук
Москва, Россия
* E-mail: af.valov@physics.msu.ru
Поступила в редакцию 08.10.2021
После доработки 15.10.2021
Принята к публикации 20.10.2021
- EDN: AKDZNI
- DOI: 10.31857/S0207401X22050107
Аннотация
Исследуется динамика пробных частиц, испытывающих смещенную диффузию под влиянием внешней постоянной силы, в каналах переменного сечения с непроницаемыми стенками. Показано, что в зависимости от отношения ширины канала в наиболее узкой его части к характерному размеру входной части канала и от места входа частицы в сужающийся канал возникают разные флуктуационные режимы прохождения частицей узкого канала переменного сечения, различающиеся скейлинговыми показателями флуктуаций.
ВВЕДЕНИЕ
Диффузия частиц в каналах переменного сечения представляет собой широкую область исследования, которая находит свои применения в различных областях знания – физике, химии, химической физике, молекулярной и клеточной биологии [1, 2], а также в искусственных микрожидкостных системах [3, 4], задачах диффузии броуновских моторов [5] и процессах, сопровождающих сорбцию частиц краун-эфирами и каликсаренами [6]. Обычно такие каналы можно рассматривать как последовательность широких камер, соединенных узкими изогнутыми воронками. Диффундирующие частицы, в свою очередь, могут быть полимерами [7–9] или молекулами [10–12], присутствовать в малых и больших концентрациях, образуя тем самым взвесь [13–17]. Частицы могут испытывать несмещенную диффузию или быть подвержены влиянию внешних электромагнитных сил, что является типичным для задач микрореалогии [10, 11, 14–18]. Среди широкого спектра биофизических приложений можно выделить задачи, связанные с прохождением узких каналов биополимерными молекулами, в частности перенос нейротрансмиттеров в синапсах [19], секвенирование ДНК в искусственных порах [20], а также процессы инъекции вирусной ДНК/РНК в клетки через узкую пору, соединяющую вирусный капсид с клеточной мембраной [21]. Множество других примеров, теоретических моделей, численных и экспериментальных данных представлены в обзорах [11, 12] и недавней работе [22].
С теоретической точки зрения задача о диффузии в каналах переменного сечения слишком сложна, чтобы ее можно было решить аналитически. Однако для некоторого класса задач применяется метод Фика–Якобса [23], который заключается в эффективном сведении исходной двумерной или трехмерной задачи к одномерному уравнению диффузии с некоторым потенциалом, имитирующим пространственное изменение сечения канала. Такая аппроксимация позволяет получить представление о важных физических величинах, по большей части связанных со временем прохождения сквозь канал [24–26], хотя и исключает из рассмотрения эффекты, связанные с диффузионным движением в направлении, перпендикулярном главной оси канала.
В данной работе изучается динамика частиц в двумерном канале с непроницаемой границей, а вопросы, которые мы поднимаем, находятся вне границ применимости аппроксимации Фика–Якобса. Мы рассматриваем типичную задачу активной микрореалогии с постоянной силой [27], в которой пробная частица испытывает действие постоянной силы, направленной вдоль канала. С использованием скейлинговых аргументов и численного моделирования анализируются статистические свойства траекторий частицы, диффундирующей вдоль канала. В частности, мы исследуем флуктуации частицы в самой узкой части канала в зависимости от его ширины и начального положения частицы.
МОДЕЛЬ
Рассмотрим смещенную диффузию пробной частицы вдоль канала, сформированного двумя непроницаемыми препятствиями в виде полукругов, как показано на рис. 1. Положим, что ось x совпадает с главной осью канала, в то время как ось y перпендикулярна ему.
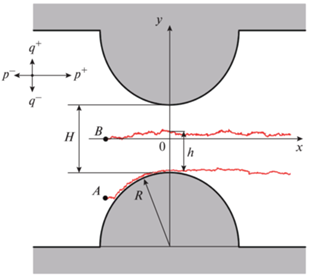
Рис. 1.
Схематическое изображение канала переменного сечения, образованного двумя симметричными полукругами радиуса R, вершины которых находятся друг от друга на расстоянии H. Пробная частица начинает свое движение либо из точки A, расположенной вблизи границы полукруга, либо из точки B, расположенной на главной оси канала. Частица движется диффузно под действием внешней силы, сонаправленной с осью x, и совершает несмещенную диффузию по оси y. Параметры p и q показывают амплитуды локальных вероятностей смещений частицы и остаются неизменными во время моделирования. Кривые, которые начинаются в точках A и B, отображают некоторые реализации траекторий пробной частицы.
Предполагается, что канал заполнен несжимаемым растворителем, который выступает в роли тепловой ванны и поддерживает постоянную температуру в системе. Пробная частица размещается на некотором расстоянии L от самой узкой части канала и начинает скачкообразное движение, которое определяется вероятностями смещения вдоль осей x и y. На каждом шаге моделирования генерируются амплитуды смещения вдоль соответствующих осей следующим образом:
(1)
$~{{P}_{x}}\left( {dx} \right)\sim \exp \left\{ {\frac{{{{{\left( {dx - \mu } \right)}}^{2}}}}{{2{{\sigma }^{2}}}}} \right\}~,\,\,\,\,{{P}_{y}}\left( {dy} \right)~\sim ~\exp \left( {\frac{{d{{y}^{2}}}}{{2{{\sigma }^{2}}}}} \right),$СКЕЙЛИНГОВЫЕ СООБРАЖЕНИЯ
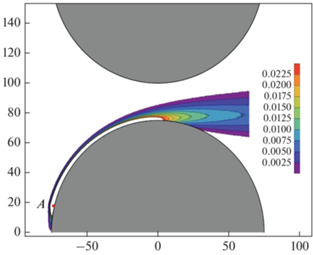
Внешняя сила, действующая на пробную частицу в продольном направлении, вынуждает последнюю следовать по прямой траектории насколько это возможно (траектория B на рис. 1), и изгибаться только в случае, если движение без изгиба невозможно (траектория A на рис. 1). Как следствие, частицы, начинающее свое движение в приграничной области, начинают “эффективно” взаимодействовать со стенкой, совершая свое движение в приграничном слое. В качестве иллюстрации на рис. 2 представлена двумерная плотность траекторий, которые стартуют в приграничной области полукруга (точка A) и проходят воронку, находясь преимущественно в некотором приграничном слое.
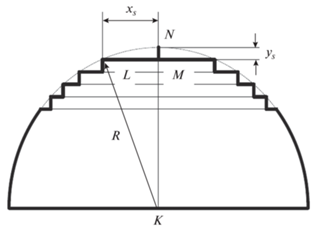
Эффективную толщину приграничного слоя можно оценить, следуя скейлинговым соображениям работ [28, 29]. В качестве вспомогательной геометрической конструкции рассмотрим аппроксимацию внешнего контура полукруга прямоугольными участками, показанную на рис. 3, и соотнесем типичные размеры приграничного слоя ${{x}_{s}}$ по оси x и ${{y}_{s}}$ по оси y, которые содержат большую часть траекторий. Исходя из геометрического соотношения
(2)
${{x}_{s}} = \left| {LM} \right| = {{\left( {{{R}^{2}} - {{{\left| {KM} \right|}}^{2}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$(3)
${{x}_{s}} = {{\left[ {{{R}^{2}} - {{{\left( {R - {{y}_{s}}} \right)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \approx {{\left( {2R{{y}_{s}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\,\,{\text{при}}\,\,{{y}_{s}} \ll R.$Рис. 2.
Контурный график массива из 400 000 траекторий, начинающихся в точке А. Цветовая схема соответствует доле траекторий, проходящих через заданную точку. Белая область внутри распределения соответствет наибольшей концентрации траекторий.
Таким образом, сопоставляя данные выражения, мы можем оценить типичные отклонения траектории от вершины полукруга, ${{y}_{s}},$ и корреляционную длину вдоль траектории, ${{x}_{s}},$ следующим образом:
ФЛУКТУАЦИОННЫЕ ХАРАКТЕРИСТИКИ ТРАЕКТОРИЙ
Статистические свойства траекторий зависят в общем случае от многих параметров: положения начальной точки, величины внешней силы, геометрии канала, температуры среды, расстояния между начальной точкой и вершиной полукруга. В данной работе нас интересует зависимость флуктуаций Var высоты h пересечения наиболее узкой части канала (см. рис. 1) от размера R препятствия:
Для изучения скейлинговых зависимостей флуктуаций пробной частицы, направленно диффундирующей в сужающемся канале с непроницаемыми стенками, мы будем измерять параметры системы в масштабах препятствий в канале. Также положим, что расстояние L между точкой старта и самым узким местом канала равно R, а ширина H самого узкого места зависит от размера полукруга следующим образом: $H = {{R}^{\alpha }}.$ При таком описании удобно ввести характерные размеры пучков траекторий, равные размерам флуктуаций в направлении, перпендикулярном каналу. Если начальная точка траектории находится вблизи полукруга, то характерный размер распределения траекторий по высоте над нижней границей воронки, согласно уравнению (4), есть $\delta \sim {{y}_{s}}\sim {{R}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$ Если же пробная частица стартует из середины канала, то характерный размер статистического ансамбля траекторий зависит от расстояния, которое проходит частица в горизонтальном направлении, т.е. $\delta \sim {{L}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{R}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$
На рис. 4 изображены зависимости показателей $\gamma $ флуктуаций высоты h пересечения траекториями наиболее узкой части канала от показателя $\alpha $ его ширины. На рис. 4а представлены данные для траекторий, которые находятся вблизи препятствия (см. рис. 1), а на рис. 4б – прямо на главной оси канала. Для наглядной демонстрации распределений и траекторий пробных частиц дополнительно приведен рис. 5.
Рис. 4.
Зависимость показателей $\gamma $ флуктуаций высоты h пересечения траекториями наиболее узкой части канала от показателя α его ширины.
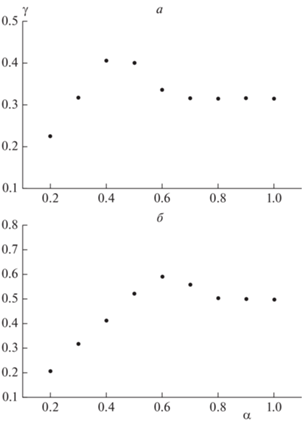
Рис. 5.
Типичные реализации траекторий частиц, движущихся вдоль канала: а, б, в – траектории, начинающиеся в точке A (см. рис. 1); г, д, е – траектории, начинающиеся на главной оси канала (точка B в рис. 1). Во всех случаях начальное расстояние L от начальной точки до центра узкого места фиксируется значением L = 500, радиус полукруга R = 500. На графиках, представленных рядом с каждой панелью, показано полученное из статистического ансамбля траекторий распределение P(h) высоты h над нижней границей воронки, в которой траектория проходит самое узкое место канала.
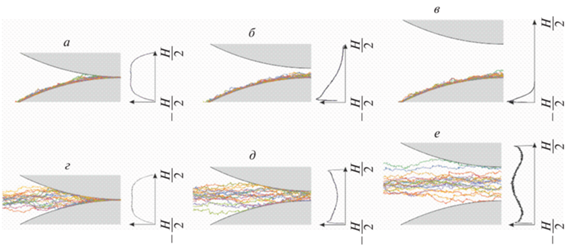
Условно поведение траекторий можно разделить на три класса, которые отличаются друг от друга относительной шириной канала, $H{\text{/}}\delta .$
1. Очень узкие каналы – $H{\text{/}}\delta \ll 1$ (области $\alpha \ll 0.3$ на рис. 4a и $\alpha \ll 0.5$ на рис. 4б). В этом случае канал является слишком узким, и траектории равномерно заполняют все свободное пространство между препятствиями (рис. 5a и б). В связи с этим показатель флуктуаций линейно растет с увеличением показателя ширины канала.
2. Каналы промежуточной толщины – $H{\text{/}}\delta \sim 1$ (области $0.3 < \alpha < 0.5$ на рис. 4a и $0.5 < \alpha < 0.7$ на рис. 4б). Роль начального положения оказывается существенной, а распределение имеет два пика, которые отвечают локализации траекторий на стенках канала. Если траектории начинаются вблизи стенки канала, то распределение P(h) сильнее локализовано на соответствующей стенке; при этом доля траекторий, которые проходят канал вблизи противоположной стенки, является существенной. Если же частица стартует с главной оси канала, то траектории достаточно быстро достигают границ канала и проходят его самое узкое место преимущественно по ним. Показатели флуктуаций в этой области выше, чем соответствующие показатели для широких каналов, из-за бимодальной формы распределений (рис. 5г и д).
3. Каналы большой толщины – $H{\text{/}}\delta \gg 1$ (области $0.5 < \alpha $ на рис. 4a и $0.7 < \alpha $ на рис. 4б). Роль начального положения является определяющей. Траектории, начинающиеся вблизи границы (точка А на рис. 1), проходят преимущественно вдоль границы (рис. 5в) и в силу продольного дрифта не доходят до противоположной границы, поэтому они имеют унимодальное распределение высот вблизи соответствующей границы. Напротив, траектории, которые начинаются на главной оси канала (рис. 5е) слишком коротки, чтобы полностью локализоваться на границах, поэтому их распределение по высоте имеет трехмодальную форму, которая с увеличением H приводится к распределению Гаусса с центром на главной оси канала.
ЗАКЛЮЧЕНИЕ
В данной работе мы изучали пространственные характеристики частицы, испытывающей смещенную диффузию в канале переменного сечения, ограниченного непроницаемыми стенками. Более конкретно, мы изучали, используя скейлинговые соображения и численное моделирование, флуктуационное поведение пробных частиц в каналах с полукруговыми препятствиями, ширина которого является степенной функцией размера препятствия ($H = {{R}^{\alpha }}$). В результате показано, что показатель флуктуаций сильно зависит от отношения ширины канала в наиболее узкой его части к характерному размеру входа в канал, а также от места входа частицы в сужающийся канал.
Авторы благодарны С. Нечаеву и Г. Ошанину за многочисленные обсуждения и ценные замечания.
Список литературы
Malgaretti P., Pagonabarraga I., Rubi J.M. // Front. Phys. 2013. V. 1. P. 21.
Kabachinski G., Schwartz T.U. // J. Cell Sci. 2015. V. 128. № 3. P. 4223.
Stone H., Stroock A., Ajdari A. // Ann. Rev. Fluid Mech. 2004. V. 36. № 1. P. 381.
Mukhopadhyay A., Granick S. // Curr. Opinion Coll. & Interface Sci. 2001. V. 6. № 5. P. 423.
Иким М.И., Дехтярь М.Л., Розенбаум В.М., Бугаев А.С., Трахтенберг Л.И. // Хим. физика. 2020. Т. 39. № 3. С. 80.
Громов В.Ф., Иким М.И., Герасимов Г.Н., Трахтенберг Л.И. // Хим. физика. 2021. Т. 40. № 1. С. 55.
Palyulin V.V., Ala-Nissila T., Metzler R. // Soft Matter. 2014. V. 10. P. 9016.
Sakaue T. // Polymers. 2016. V. 8. P. 424.
Bianco V., Malgaretti P. // J. Chem. Phys. 2016. V. 145. № 11.
Burada P.S., Schmid G., Reguera D., Rubí J.M., Hänggi P. // Phys. Rev. E. 2007. V. 75. P. 051111.
Burada P.S., Hänggi P., Marchesoni F., Schmid G., Talkner P. // Chem. Phys. Chem. 2009. V. 10. № 1. P. 45.
Rubi J.M. // Europhys. Lett. 2019. V. 127. № 1. P. 10001.
Zilman A. // Biophys. J. 2009. V. 96. № 4. P. 1235.
B’enichou O., Illien P., Oshanin G., Sarracino A., Voituriez R. // Phys. Rev. Lett. 2015. V. 115. P. 220601.
B’enichou O., Illien P., Oshanin G., Sarracino A., Voituriez R. // J. Phys.: Cond. Matt. 2018. V. 30. № 44. P. 443001.
Reichhardt C.J.O., Reichhardt C. // Ibid. P. 244005.
Puertas A.M., Malgaretti P. // J. Chem. Phys. 2018. V. 149. P. 174908.
Malgaretti P., Pagonabarraga I., Rubi J. // Ibid. 2016. V. 144. P. 034901.
Schuss Z., Singer A., Holcman D. // Proc. Nat. Ac. Sci. 2007. V. 104. P. 16098.
Chinappi M., Cecconi F. // J. Phys.: Cond. Matt. 2018. V. 30. P. 204002.
Marenduzzo D., Orlandini E., Stasiak A. et al. // Proc. Nat. Ac. Sci. 2009. V. 106. P. 22269.
Malgaretti P., Oshanin G., Talbot J. // J. Phys.: Cond. Matt. 2019. V. 31. P. 270201.
Zwanzig R. // J. Phys. Chem. 1992. V. 96. P. 3926.
Kalinay P., Percus J.K. // Phys. Rev. E. 2006. V. 74. P. 041203.
Mangeat M., Guerin T., Dean D. // J. Stat. Mech.: Theo. and Exp. 2017. P. 123205.
Malgaretti P., Oshanin G. // Polymers. 2019. V. 11. P. 251.
Wilson L.G., Poon W.C.K. // Phys. Chem. Chem. Phys. 2011. V. 13. P. 10617.
Nechaev S., Polovnikov K., Shlosman S., Valov A., Vladimirov A. // Phys. Rev. E. 2019. V. 99. P. 012110.
Valov A., Avetisov V., Nechaev S., Oshanin G. // Phys. Chem. Chem. Phys. 2020. V. 22. P. 18414.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика