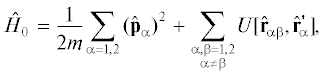Химия твердого топлива, 2020, № 3, стр. 68-72

ВВЕДЕНИЕ

Известно, что запасы традиционных источников энергии (уголь, газ, нефть и пр.) довольно ограничены. Помимо этих источников, которые являются невозобновляемыми, используются и возобновляемые источники (солнечные батареи, ветряные и гидроэлектростанции, органическое неископаемое топливо). Однако они не могут удовлетворить современные потребности, поэтому не вызывает сомнения актуальность и исключительная важность подходов к поиску нетрадиционных способов получения энергии. В настоящей работе представлены исследования по генерации энергии из атомов гелия, который является вторым по распространенности (после водорода) элементом, при этом постоянно образующимся из водорода в ядрах солнцеподобных звезд, поэтому есть вероятность того, что он станет в будущем самым распространенным элементом. Возможность такой генерации показана в расчетах на основе разработанного принципиально нового прямого вариационного метода квантовой химии, основанного на использовании априорного определения узлов волновой функции (узлы – точки конфигурационного пространства, в которых волновая функция обращается в нуль), позволяющего рассчитывать состояния атомов гелия в сильных и сверхсильных электрических и магнитных полях в отличие от традиционных методов решения уравнения Шредингера [1, 2]. Обычные расчетные методы квантовой химии не позволяют в принципе оценить возможности и условия получения энергии из атомов гелия, что связано не только с тем, что используемая в них теория возмущений не позволяет моделировать процессы с энергиями, бóльшими энергии основного (невозмущенного, т.е. в отсутствие поля) состояния атомов, но и с тем, что они не сопоставимы по точности расчетов с теорией, приведенной в работе [2].

Следует отметить, что упомянутые ограничения современных методов квантовой химии связаны с трудностями решения уравнения Шредингера для многоэлектронных систем, когда для его решения используется приближение Хартри–Фока.

В работах [2–6] это приближение не используется, в его основе лежит альтернативная методология, позволяющая осуществить математически строгое разделение переменных [7] при решении уравнения Шредингера. Это снимает ограничения существующих квантово-химических методов, повышает точность расчетов, что позволяет оценить условия получения энергии из атомов гелия, – решение этих круга проблем и явилось целью настоящего исследования.

ОСНОВНАЯ ЧАСТЬ

Как известно [8], принцип запрета Паули (ПЗП) сформулирован как запрет двум электронам в атоме иметь одновременно четыре совпадающих квантовых числа. Автор [9] трактовал ПЗП как требование антисимметричности волновых функций, и все известные методы квантовой химии используют в качестве обязательного условия решения уравнения Шредингера именно это требование. Фактически это ведет к тому, что, хотя гамильтониан и не зависит от спина, спиновые и координатные переменные не разделяются. Именно это положение и определяет одну из главных трудностей в нахождении волновых функций системы тождественных частиц, если не исходить заранее из одночастичного приближения [10].

В [11, 12] было показано, что антисимметрия для N-электронной системы математически эквивалентна существованию узловой поверхности размерности 3N–1 в 3N-мерном конфигурационном пространстве, в которой волновая функция системы обращается в нуль. Преимущество перед известными в квантовой химии расчетными методами в данном случае состоит в том, что требования антисимметрии (т.е. принцип Паули) заменяется системой узловых поверхностей, разделяющих N! областей конфигурационного пространства. При этом все эти области можно полагать эквивалентными в том смысле, что они дают одинаковые вклады в расчет наблюдаемых величин (например, в величину энергии), что обеспечивает возможность разделения спиновых и пространственных переменных, так как каждая из этих областей определяется распределением спинов. Для четных N число областей будет равным $\frac{{N!}}{{\left( {\frac{N}{2}} \right)!\left( {\frac{N}{2}} \right)!}}$, а для нечетных N – $\frac{{N!}}{{\left( {\frac{N}{2} + \frac{1}{2}} \right)!\left( {\frac{N}{2} - \frac{1}{2}} \right)!}}$, каждая из которых, в свою очередь, делится на ${{\left[ {\left( {\frac{N}{2}} \right)!} \right]}^{2}}$или $\left[ {\left( {\frac{N}{2} + \frac{1}{2}} \right)!\left( {\frac{N}{2} - \frac{1}{2}} \right)!} \right]$ подобластей, причем все они эквивалентны в вышеозначенном смысле.

Таким образом, в нашем подходе требование формальной антисимметричности (т.е. принцип Паули [8] в формулировке Гейзенберга [9]) заменяется системой узловых поверхностей, разделяющих N! областей конфигурационного пространства. Это означает, что базисные функции в прямых вариационных методах содержат необходимые граничные условия, а сами функции, определяемые для одной области, могут быть, как указывалось выше, произвольной симметрии или даже не обладать симметрией вовсе. Это существенно расширяет класс пробных функций в прямых вариационных расчетах. Новый подход позволяет в N! раз сократить расчетную процедуру и дает возможность повысить точность и эффективность расчетов.

Вначале эта методология была использована для расчетов энергетических состояний атомов гелия [1]. Проведенные расчеты 1s(¹S)- и 1s2s(³S)-состояний практически повторяют результаты работ [13, 14] для атома гелия (¹S). Однако различия в а.е. имеются в 7-м знаке после запятой (следует напомнить, что 1 а.е. = 627.5095 ккал/моль) и авторами достигнута бóльшая точность, что позволило получить лучшее из всех известных значений для энергии основного состояния He (–2.90372445 а.е.) при использовании всего 47 базисных функций, в то время как наиболее точное из представленных в литературе [15] значений (–2.90372438 а.е.) было получено при использовании 1078 функций.

Повышение эффективности квантово-химических расчетов и соответствующее повышение точности связано со следующим обстоятельством. Для расчетов основного состояния атома He обычно используется пробная волновая функция (ВФ) вида [4]

Разделение пространства на r₁ ≤ r₂ и r₁ ≥ r₂ дает возможность использовать в качестве пробной следующую волновую функцию:

т.е. освободиться от жесткого ограничения на коэффициенты при ВФ и, таким образом, значительно расширить класс пробных функций [2]. Очевидно, что класс симметричных многочленов – лишь малая часть всех многочленов и это расширение очень существенно.

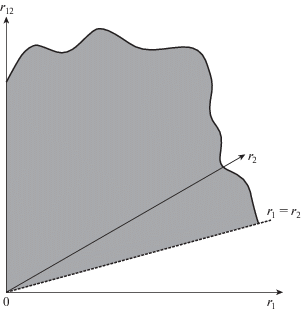
Следует также отметить, что расчеты триплетного атома He, приведенные в статье, принципиально отличаются от общепринятых. Поясним, с чем это связано. У волновой функции Ψ (r₁, r₂, r₁₂) двух электронов с координатами r₁ и r₂ и совпадающими спинами координатная часть функции должна быть антисимметричной по перестановке переменных r₁ и r₂. Это означает, что при r₁ = r₂ волновая функция обращается в нуль. На плоскости это равенство определяет прямую, которая разделяет плоскость на две области: Ω_I при r₁ ≥ r₂ и Ω_II при r₂ ≥ r₁ (рис. 1). Поэтому волновую функцию следует определять не для всей плоскости (r₁r₂), а лишь для одной из ее полуплоскостей (например, Ψ^I(r₁, r₂) для полуплоскости Ω_I) и далее отразить найденную функцию антисимметричным образом в другую полуплоскость:

Для того, чтобы при таком отражении полная волновая функция и плотность потока сохраняли непрерывность [16], достаточно задать граничные условия:

Этот же прием при расчетах для синглетного состояния не требует наложения соответствующих граничных условий, а пробные функции продолжаются симметричным отражением в смежную область. Следует отметить, что отражение функции Ψ^I или Ψ^II в другую область не является обязательным для нахождения наблюдаемых величин, если функцию в одной из этих областей нормировать на единицу.

При расчетах триплетного, т.е. ³S-состояния атома He использовались граничные условия (1), а не заранее антисимметризованная функция. Конфигурационное пространство в данном случае есть {r₁r₂r₁₂}, и в этом пространстве замена частиц означает замену r₁ и r₂, в то время как r₁₂ = r₂₁. Поэтому двумерная плоскость r₁ = r₂ разделяет пространство на две части и решение можно искать только для r₁ ≥ r₂ (или же для r₂ ≥ r₁), а для волновой функции использовать граничное условие (1). Основное практическое преимущество этого подхода состоит в том, что класс функций, которыми можно приближать истинное решение, существенно расширяется, так как множество симметричных полиномов {$\Psi _{n}^{s}$} является подмножеством произвольных полиномов {$\Psi _{n}^{p}$}, что естественно приводит к более быстрой сходимости и подтверждается проведенными расчетами. Расчеты энергии ³S-состояния атома He с 47 варьируемыми коэффициентами дали величину энергии –2.1752288 а.е., а при экспериментальном значении –2.175230 а.е. [15], что также превышает по точности вычислений и минимуму числа базисного набора функций все известные расчеты.

Кроме того, разработки [1], как указывалось выше, позволяют оценить условия и возможности получения принципиально нового способа получения энергии [2, 17], поскольку описывают состояния атомов в сильных и сверхсильных электрических и магнитных полях. Действительно, для промежуточных состояний напряженности поля, когда эти величины оказываются соизмеримы с внутриатомными полями, гипотетически возможны узловые поверхности, соответствующие уровням состояний выше основного, и тогда эти состояния метастабильны, или же эти состояния оказываются ниже основного и являются суперстабильными [2], т.е. переход, связанный с ними, происходит с выделением энергии. В первом случае атомы накапливают энергию соответствующего поля, которая затем может выделиться при его “выключении”, а во втором случае поле служит подобием катализатора процесса и атомы самопроизвольно не возвращаются в исходные состояния после выделения энергии. Именно переход в это состояние и можно рассматривать как принципиально новый источник энергии.

Гамильтониан атома гелия во внешнем магнитном поле можно записать в виде

а гамильтониан невозмущенного атома гелия: где ${\mathbf{\hat {L}}}$ – оператор орбитального момента, ${\mathbf{\hat {S}}}$ – оператор спина электрона, µ – гиромагнитное отношение, m и e – масса и заряд электрона, с – скорость света, H – напряженность внешнего магнитного поля, α – номер электрона (в атоме гелия их два), ${{{\mathbf{\hat {r}}}}_{\alpha }}$, ${{{\mathbf{\hat {p}}}}_{\alpha }}$ – операторы радиус-вектора и импульса электрона α, ${\mathbf{\hat {r}}}_{\alpha }^{{\text{'}}}$ – оператор расстояния между ядром и электроном α, ${{{\mathbf{\hat {r}}}}_{{\alpha \beta }}}$ – оператор расстояния между электронами, $U[{{{\mathbf{\hat {r}}}}_{{\alpha \beta }}},{\mathbf{\hat {r}}}_{\alpha }^{{\text{'}}}]$ – энергия взаимодействия электронов друг с другом и ядром.

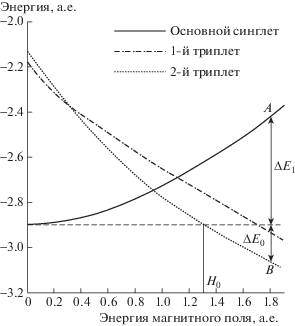
Как видно из рис. 2, в магнитном поле энергия основного синглетного уровня (Н₀ = –2.903 а.е.) повышается вместе с повышением энергии магнитного поля. Триплетные уровни при этом понижаются и при энергии ≈1.3 а.е. [2] уровни пересекаются. Если, например, при энергии поля, равной 1.8 а.е., вызвать переход из состояния A в состояние B, то выделится энергия, равная сумме ∆Е₁ (энергия поля) и ∆Е₀ (разность энергий основного и суперстабильного состояний). Собственно, ∆Е₀ и есть выигрыш в энергии по сравнению с затраченной работой магнитных сил A = ∆Е₁.

В принципе, переход “синглет–триплет” запрещен, однако для отдельного атома (в основном, синглетном состоянии) можно превысить напряженность магнитного поля 1.3 а.е. (при этом происходит инверсия уровней), а затем (для “выбранной” напряженности поля) подействовать на атом поляризованным по спину (с нужной ориентацией, зависящей от напряженности поля) пучком электронов и тем самым индуцировать переход “синглет–триплет” с заданной частотой, определяемой выбором величины магнитного поля. При этом получится выигрыш в энергии (по сравнению с энергией поля), а сам атом будет переведен в суперстабильное состояние [2]. Так, при 1.8 а.е. происходит выделение энергии, равное 102.4 ккал/г, из которой 27.6 ккал/г приходится, собственно, на “выигрыш”, т.е. на разность энергий основного и суперстабильного состояния атома гелия. При 2.0 а.е. уже получается, соответственно, 150 и 40 ккал/г, а при 3.0 а.е. – 400 и 100 ккал/г, а при напряженности магнитного поля в 2–3 а.е. выход энергии на 1 г вещества в тысячи раз выше, чем в самых мощных химических процессах (например, при горении металлов). Для таких процессов максимальная энергия (5.79 ккал/г) выделяется при горении бериллия в атмосфере фтора [18].

Следует отметить, что представленные выше теоретические разработки относятся к отдельным атомам Не. Очевидно, что осуществить этот процесс для вещества (т.е. для очень большого количества атомов He) возможно лишь для твердого состояния. В газообразном или даже в жидком состоянии электроны будут “обмениваться” спинами при “столкновениях” и ожидаемого эффекта не произойдет. Известно, что гелий – это единственное вещество, которое не переходит в обычных условиях в твердое состояние вплоть до абсолютного нуля, превращаясь в жидкость только при 4.2 K, поэтому обнаружить атомы гелия в суперстабильном состоянии в природе не представляется возможным. Однако твердый гелий получается при достаточно высоких давлениях [19].

ЗАКЛЮЧЕНИЕ

Таким образом, разработанный метод квантовой химии и выполненные на его основе расчеты позволяют заключить, что возможен принципиально новый способ получения энергии из атомов гелия, а также оценить условия генерации этой энергии. В настоящее время не представляется возможным ответить на вопрос о возможности существования суперстабильных состояний других атомов, поскольку для этого требуется проведение достаточно сложных вычислений, выполнение которых возможно лишь на основе представленного выше метода МВФ.

Конечно, получать энергию таким способом в настоящее время нерационально, но описанный процесс позволяет создать некий аналог лазера, т.е. источник когерентного излучения, мощность которого в тысячи (и даже в миллионы) раз превосходит все известные источники лазерного излучения, причем заранее выбранной экспериментатором частоты.