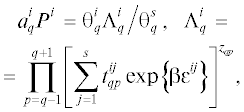Кинетика и катализ, 2019, T. 60, № 4, стр. 440-449

УСРЕДНЕНИЯ МОДЕЛИ ШЕРОХОВАТОЙ ПОВЕРХНОСТИ

Молекулярная модель адсорбции основана на модели решеточного газа [3, 15, 17]. Объем системы разбивается на отдельные элементарные ячейки со стороной размером с диаметр молекулы (λ) и объемом ячейки ${{\text{v}}_{0}}.$ Рассматривается плоская граница раздела жидкость–пар. На границе раздела ячейки объединяются в монослои (с номером q-прилегающего к границе монослоя жидкости), в которых они характеризуются числом связей с ближайшими соседями z_qp из монослоя p. Значение q = 1 отвечает плотной фазе, а q = κ – паровой фазе. Обозначим в переходной области между сосуществующими фазами локальные плотности частиц адсорбента A через $\theta _{q}^{{\text{A}}}$ и локальные плотности молекул адсорбата В (или В₂) через $\theta _{q}^{{\text{B}}}.$ Плотности для слоев q = 1 и q = κ считаются фиксированными (они находятся из условия расслаивания системы при исходной температуре T₁).

Рассматриваются межмолекулярные взаимодействия между ближайшими соседями (в пределах одной координационной сферы). Параметры энергетических взаимодействий компонентов системы обозначим через $\varepsilon _{{qp}}^{{ij}}$ = ε_ij.

На рис. 1 приведена схема распределения частиц адсорбента A (серые квадраты) и вакансий V (белые квадраты) в переходной области между фазами шириной (κ – 2) (где q = 1 – монослой конденсированной фазы, а q = 8 = κ – монослой пара). Эта схема отвечает исходной усредненной полислойной модели с разными типами центров адсорбции (характеризующиеся своими константами Генри), содержащей все доступные для адсорбции центры, и три типа ее усреднения [16].

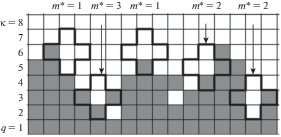
Адсорбция происходит на свободных узлах. На рис. 1 вокруг вакантных узлов выделены кластеры из их ближайшего окружения, тип которых определяется числом m* входящих в них частиц A. Значение m* определяет константу Генри центрального узла кластера. В первой модели вакантные узлы на рис. 1 распределяются по типам в зависимости от расстояния от плотной фазы, что задается номером монослоя q, и от состояния их окружения в кластере, что задается множеством чисел {m_qp} частиц А в монослое p рядом с центральным узлом из монослоя q. Заданное множество чисел {m_qp} отвечает номеру σ-конфигурации кластера с одним центральным узлом в монослое q.

Решение системы уравнений для первой модели требует решения системы уравнений большой размерности. Результаты анализа первой модели представлены в работе [16]. На практике стараются использовать различные усредненные модели с меньшей размерностью системы уравнений. Рассмотрим следующих три типа усреднений первой модели, подробно описанные в статье [16].

Модель 2, усредненная по монослоям с разделением типов по константе Генри. При данном усреднении различаются только узлы, имеющие разное значение константы Генри, т.е. характеризуются только собственным целочисленным значением m*. Всего в модели z типов узлов в переходной области.

Модель 3, усредненная по константе Генри внутри каждого монослоя. В данной модели шероховатой поверхности каждый тип узла, доступного для адсорбции, определяется только номером монослоя q, который однозначно задает усредненные нецелочисленные значения чисел А в окружении центрального узла по монослоям {${{\hat {m}}_{{qp}}}$}, усредненных по монослою q для каждого соседа p в отдельности. Всего в модели (κ – 2) типа узлов в переходной области.

Полностью усредненная модель 4. В данной модели шероховатой поверхности все узлы, доступные для адсорбции, принадлежат одному типу и описываются общим средним нецелочисленным значением $\hat {m}$ числа частиц А в окружении узла, усредненным по всему объему переходной области. Всего в модели 4 имеется единственный тип узлов, доступных для адсорбции.

На рис. 2 показано усреднение по трем моделям: а – модель 4, б – модель 3, в – модель 2. На рис. 2 (подобно рис. 1а) изображены схемы распределения частиц A (серые квадраты) с детальным разбиением вакантных ячеек на типы: белые ячейки – это вакантные места, полностью окруженные частицами А (т.е. изолированные), а заштрихованные ячейки – места, доступные для адсорбции. Доступным для адсорбции ячейкам одного типа (на схемах помечены другим типом штриховки) присвоены номера от 1 до 6. Так, в полностью усредненной модели 4 (рис. 2а) все ячейки, кроме занятых частицами А (серые) и изолированных (белые), помечены одинаковой штриховкой и обозначены номером 1.

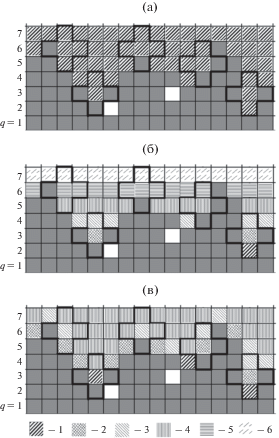
На рис. 2б на схеме переходной области модели 3 ячейки из одного монослоя q закрашены одним типом штриховки, которая в итоге меняется послойно от номера 1 до номера 6. А на рис. 2в штриховка ячейки зависит от общего числа m* частиц А в ближайшем ее окружении: например, штриховка номер 1 (если в ближайшем окружении ячейки имеется 3 частицы А), номер 2 (если 2 частицы А), номер 3 (если 1 частица А) и номер 4 (если нет ни одной частицы А). В итоге получаем, что в модели 2 номер 1 присвоен ячейкам, в которых наибольший потенциал поля адсорбента, и доля таких ячеек от всех заштрихованных минимальна. Чем больше номер штриховки ячеек, тем меньше в них потенциал поля адсорбента. В модели 4 потенциал поля для ячейки из монослоя q усреднен по всем ячейкам из данного монослоя, и, как следует из рис. 2б, потенциал поля адсорбента будет убывать с каждым последующим монослоем q (т.е. с ростом номера штриховки), а доля соответствующих ячеек от всех заштрихованных будет возрастать. Более подробно распределение узлов по энергетическим уровням описано в работе [22].

УРАВНЕНИЯ МОДЕЛИ ШЕРОХОВАТОЙ ПОВЕРХНОСТИ [22–24]

При равновесном состоянии поверхности адсорбента при температуре T₁ граница адсорбента имеет шероховатую структуру из-за температурного размывания области границы. Если затем температура резко понижается до некоторой температуры Т < T₁, при которой изучается адсорбция, то формируется профиль поверхности – закаленная равновесная поверхность. На этих двух типах поверхностей рассмотрим процесс адсорбции частиц В.

В равновесном состоянии шероховатой поверхности происходит перераспределение атомов А (идет перестройка границы раздела фаз) в ходе процесса адсорбции частиц В. Локальные плотности $\theta _{q}^{{\text{A}}}$ и $\theta _{q}^{{\text{B}}}$ получаются из решения следующей системы уравнений в КХП учета латерального взаимодействия между частицами при заданной температуре T:

где $a_{q}^{i}$ – локальная парциальная константа Генри для молекулы i на узле типа q, β = 1/(R_BT), R_B – газовая постоянная, Pⁱ – давление компонента i, $t_{{qp}}^{{ij}}$ – условная вероятность нахождения молекул компонентов i и j (1 ≤ i, j ≤ s, где s – вакансии) в слоях q и p, ε^ij – энергия взаимодействия частиц i и j, описываемая потенциальной функцией Леннард–Джонса. Функция неидельности $\Lambda _{q}^{i}$ учитывает весь спектр конфигураций соседних частиц.

Адсорбция на закаленной поверхности рассчитывается в два этапа.

Первый этап. Сначала рассчитывается $\theta _{q}^{{\text{A}}}$ – профиль А в отсутствие В по уравнениям (1). Затем по профилю плотностей $\theta _{q}^{{\text{A}}}$ и условным вероятностям $t_{{qp}}^{{{\text{AA}}}}$ = $\theta _{{qp}}^{{{\text{AA}}}}$/$\theta _{q}^{{\text{A}}}$ рассчитывается локальная структура переходной области адсорбента [22] с помощью функций вероятности кластеров: 1) с одним центральным узлом из монослоя q и числами частиц A m_qp в его окружении из монослоев p, $\Theta _{q}^{{{\text{V}}|\sigma }},$ где верхний индекс V|σ указывает, что в центральном узле располагается вакансия V, а состояние окружающих его узлов отвечает типу σ-конфигурации кластера с одним центральным узлом, и 2) c двумя центральными узлами из монослоев q и h и числами частиц A m_qp и m_hk в его окружении из монослоев p и k соответственно, $\Theta _{{qh}}^{{{\text{VV}}|\sigma \delta }},$ где верхний индекс VV|σδ указывает, что в центральных узлах располагаются вакансии VV, а состояние узлов, окружающих первый и второй центральные узлы, отвечает типам σ- и δ-конфигурации кластера с одним центральным узлом соответственно.

Второй этап. В переходной области “закаленного” твердого тела А рассчитывается профиль плотности адсорбата В, $\theta _{q}^{{{\text{B}}|\sigma }},$ по уравнению, в котором в знаменателе учитывается локальный потенциал поля $Q_{q}^{\sigma }$ адсорбента в константе Генри

где $Q_{q}^{{\sigma }} = {{{\varepsilon }}^{{{\text{BA}}}}}\sum\nolimits_{p = q - 1}^{q + 1} {{{m}_{{qp}}}} ,$ $S_{{qh}}^{{{\sigma \delta }}}$ = 1 + $t_{{gh}}^{{\sigma \delta }}$x^BB, x^BB = = exp{–βε^BB} – 1, $t_{{qh}}^{\sigma }$ – условная вероятность нахождения молекул B в ячейках заданного типа, $d_{{qh}}^{{\sigma \delta }}$ = $\Theta _{{qh}}^{{{\text{VV}}|\sigma \delta }}$/Σ_δ$\Theta _{{qh}}^{{{\text{VV}}|\sigma \delta }}.$

Уравнения на парные функции распределения в КХП записываются в виде

Нормировочные соотношения для парных функций компонентов ${\theta }_{{qp}}^{{ij}}$ имеют вид: $\sum\nolimits_{i = 1}^s {{\theta }_{{qp}}^{{ij}}} = {\theta }_{p}^{j}$ и $\sum\nolimits_{j = 1}^s {{\theta }_{{qp}}^{{ij}}} = {\theta }_{q}^{i},$ а для унарных функций они равны $\sum\nolimits_{i = 1}^s {{\theta }_{q}^{i}} = 1.$

УРАВНЕНИЯ СКОРОСТЕЙ АДСОРБЦИИ–ДЕСОРБЦИИ

Скорости адсорбции–десорбции молекул B выражаются через введенные одноузельные ${\theta }_{q}^{i}$- и двухузельные $t_{{qp}}^{{ij}}$-корреляторы. Уравнения скоростей адсорбции и десорбции одноузельной стадии (без диссоциации) приведены в статье [16]. Ниже приводятся выражения скоростей адсорбции и десорбции двухузельной стадии (с диссоциацией) для полностью распределенной модели 1.

Скорость адсорбции двухузельной стадии на равновесной поверхности описывается уравнением (3а):

где $\hat {K}_{{gh}}^{{{\text{VV}}}}$ – константа скорости, $\delta {{\varepsilon }^{{{\text{V}}j}}}$ = ${{\varepsilon }^{{{\text{V}}j*}}}$ – ε^Vj = = ε^Vj* = ε^Bjα_ε, α_ε – параметр активированного комплекса, 0 < α_ε < 1.5 (в работе принималось α_ε = 0.5), ${{\Delta }_{{hf}}}$ – символ Кронекера, $f \in z\left( q \right)$ – координационная сфера узла из монослоя q.

Скорость десорбции двухузельной стадии на равновесной поверхности описывается уравнением (3б):

где δε^Bj = ${{{\varepsilon }}^{{{\text{B}}j*}}}$ – ε^Bj = ε^Bj(α_ε – 1).

Скорость адсорбции двухузельной стадии на закаленной поверхности описывается уравнением (3в):

Скорость десорбции двухузельной стадии на закаленной поверхности описывается уравнением (3г):

Применение усреднения к модели изменяет вид функций неидеальности $S_{{qh}}^{{ii}}$ и $S_{{qh}}^{{ii|\sigma \delta }}.$ Ниже выписаны примеры функций неидеальности для трех усредненных моделей закаленной равновесной поверхности (для равновесия они имеют аналогичный вид с добавлением в сумму по компонентам j компонент А).

В модели 4 с единственным типом узлов получаем:

В модели 3, усредненной по константе Генри внутри каждого монослоя q и h, имеем:

В модели 2, усредненной по монослоям, с выделением типов ξ и ζ по константе Генри (в зависимости от числа контактов с адсорбентом m*), получаем:

ПАРАМЕТРЫ ЧИСЛЕННОГО АНАЛИЗА

Условие самосогласованности рассматривается на примере хемосорбции без диссоциации В и с диссоциацией В₂ на поверхности твердого тела А, моделируемого для простоты изотропной решеткой с малой шириной переходной области κ = 5 (что отвечает температуре вблизи плавления вещества А). (Для более реальной модели твердого тела нужен учет присутствия других граней твердого тела.)

Напомним [3, 14], что взаимное отталкивание хемосорбированных частиц описывается отрицательными параметрами латерального взаимодействия, а притяжение физически адсорбированных частиц – положительными. За основу энергетических соотношений выбрана величина ε_АА энергии взаимодействия компонентов адсорбента А, и ε_АB = 0.15ε_AA и ε_BB = –0.33ε_AB. Величина ε_АА условно выбрана за единицу, что относит рассчитанные результаты к системам разного типа и дает относительные корреляции между ними.

Адсорбция газа B рассматривается при сверхкритической температуре. В качестве условной меры для давления в данной работе введена величина $P_{n}^{{\text{B}}},$ при которой числовая плотность флюида в объеме равна 0.5. По отношению к ней рассматриваются различные значения давлений указанных систем.

Для хемосорбции область изменения заполнения переходной области ограничена монослоем. Так как взаимодействие между адсорбентом и адсорбатом сильное, то монослой заполняется при давлениях $P_{{\text{m}}}^{{\text{B}}}$ в несколько раз меньше, чем $P_{n}^{{\text{B}}},$ а именно: $P_{{\text{m}}}^{{\text{B}}}$/$P_{n}^{{\text{B}}}$ равно 0.12 для закаленной равновесной поверхности, 0.375 для равновесной поверхности в КХП и 0.25 для равновесной поверхности в ПСП для рассматриваемых параметров.

КОНЦЕНТРАЦИОННЫЕ ПРОФИЛИ А И В НА ГРАНИЦЕ РАЗДЕЛА ФАЗ

Для того чтобы исследовать строго равновесный концентрационный профиль адсорбента А при адсорбции газа В в его переходной области около температуры плавления вещества А, необходимо рассмотреть ситуацию, когда в систему с двухфазным состоянием вещества А добавляется газ В, который смешивается с паром А и заполняет его переходную область А (но не растворяется внутри конденсированной фазы А). Адсорбция В меняет концентрационный профиль адсорбента.

На рис. 3 представлены концентрационные профили твердого вещества А (кривые 1) и газа В (кривые 2) в переходной области (1 < q < κ) вблизи температуры плавления. Множество кривых под одной цифрой (1 или 2) относится к различным значениям давления В (P^B), которое варьируется от нуля до давления, при котором монослой на поверхности адсорбента заполняется до 50%. Стрелки рядом с цифрами 1 и 2 указывают, куда смещаются профили из соответствующего множества кривых с ростом давления P^B в газе.

Рис. 3 показывает, что, начиная с некоторого давления, присутствие компонента В в переходной области изменяет профиль плотности А. В ходе дальнейшего увеличения P^B плотность А в центральном монослое переходной области растет, приводя к уменьшению степени шероховатости поверхности твердого вещества А.

Кривые $\theta _{q}^{i}$ на рис. 3, представляющие собой доли от всего объема монослоя q, которые занимают частицы i, полностью согласуются с обычными представлениями о повышенной концентрации компонента В на поверхности адсорбента А. При расчете величины адсорбции требуется пересчитать плотность В в монослое q к доле объема монослоя q, свободного от частиц А, т.е. (1 – $\theta _{q}^{{\text{A}}}$). В результате получаем величину $\theta _{q}^{{\text{B}}}$/(1 – $\theta _{q}^{{\text{A}}}$), представляющую собой реальную плотность в данном монослое q, которая входит в полную изотерму адсорбции (рис. 4).

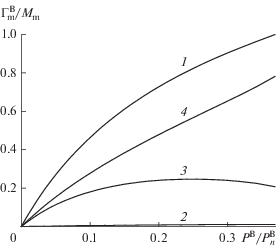
На рис. 4 представлены изотермы хемосорбции В на равновесной поверхности А при температуре вблизи плавления А для двух последних моделей: по модели 4 (полное усреднение) построена кривая 1 как общее количество адсорбата ${\text{Г }}_{{\text{m}}}^{{\text{B}}}$ на монослое поверхности адсорбента А, отнесенное к емкости монослоя M_m, и по модели 3 (различаются монослои) построены кривые 2, 3 и 4 как локальные величины (${\text{Г }}_{{\text{m}}}^{{\text{B}}}$)_q для монослоев q = 2, 3 и 4 соответственно, отнесенные к емкости монослоя M_m. По оси абсцисс отложено давление В в газе (P^B), нормированное на величину давления $P_{n}^{{\text{B}}}.$

Согласно рис. 4, величина адсорбции в монослое q = 2 (кривая 2) крайне мала. Это связано с малой долей адсорбционных мест, поскольку данный монослой практически полностью состоит из частиц А, плотность которых в нем близка к плотности твердой фазы А. В монослое q = 3 (кривая 3) величина адсорбции изменяется с появлением максимума на кривой. Снижение же величины адсорбции В в монослое q = 3 в области давлений 0.25 < P^B < $P_{n}^{{\text{B}}}$ объясняется тем, что с повышением давления P^B происходит перестройка поверхности адсорбента таким образом, что увеличивается концентрация его частиц в данном монослое q = 3 и, начиная с давления, когда адсорбат B заполняет все свободное пространство в монослое, дальнейшее увеличение концентрации А в монослое ведет к вытеснению частиц В (см. рис. 3). В монослое q = 4 (кривая 4) величина адсорбции увеличивается практически линейно с ростом P^B благодаря увеличению площади поверхности адсорбента А, частицы которого лежат в монослое q = 3. В итоге суммарная величина адсорбции ${\text{Г }}_{{\text{m}}}^{{\text{B}}},$ получаемая по полностью усредненной модели 4, монотонно увеличивается (кривая 1), пока не достигает значения емкости монослоя на поверхности адсорбента M_m.

АНАЛИЗ СКОРОСТЕЙ АДСОРБЦИИ–ДЕСОРБЦИИ

На рис. 5 показаны скорости адсорбции–десорбции на поверхности твердого вещества А газа В (U^V/U^B) без диссоциации (рис. 5а) и газа В₂ (U^VV/U^BB) с диссоциацией (рис. 5б). Все кривые адсорбции U^V и U^VV совпадают с соответствующими кривыми десорбции U^B и U^BB, поэтому на рис. 5 они помечены одним номером при температуре вблизи плавления А для двух последних моделей. По модели 4 построена кривая 1 как общая средняя скорость сорбции Uⁱ без диссоциации (рис. 5а) и Uⁱⁱ с диссоциацией (рис. 5б), а по модели 3 построены кривые 2, 3 и 4 как локальные скорости сорбции $U_{q}^{i}$ без диссоциации (рис. 5а) и $U_{{qq}}^{{ii}}$ с диссоциацией (рис. 5б) в монослоях q = 2, 3 и 4 соответственно. Скорости сорбции $U_{{qq}}^{{ii}}$ на рис. 5б показаны на примере диссоциации на однотипных узлах, т.е. в рамках модели 3 это означает, что диссоциация происходит на узлах из одного монослоя q (см. рис. 2б).

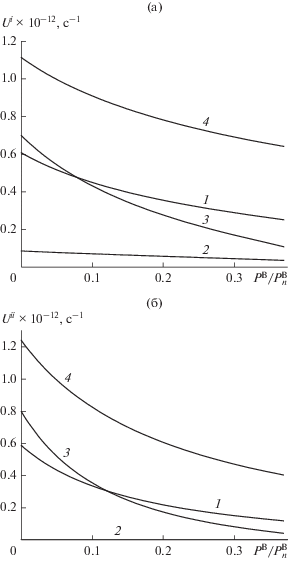
На рис. 5а и 5б видно, что все скорости адсорбции убывают с ростом P^B. Для скоростей адсорбции без диссоциации (рис. 5а) получено, что все локальные значения адсорбции $U_{q}^{{\text{V}}}$ и общее среднее значение U^V совпадают с соответствующими значениями $U_{q}^{{\text{B}}}$ и U^B процесса десорбции и образуют с ними общую кривую. Аналогично для скоростей адсорбции с диссоциацией (рис. 5б) получено, что все локальные значения адсорбции $U_{{qq}}^{{{\text{VV}}}}$ и общее среднее значение U^VV совпадают с соответствующими значениями $U_{{qq}}^{{{\text{BB}}}}$ и U^BB процесса десорбции и образуют с ними общую кривую. Таким образом, для моделей 3 и 4 мы всегда получаем строгое выполнение самосогласования уравнения изотермы адсорбции с уравнениями скоростей адсорбции как без диссоциации В, так и с диссоциацией В₂.

На рис. 6а представлены скорости адсорбции–десорбции газа В₂, U^VV/U^BB (все кривые адсорбции U^VV совпадают с соответствующими кривыми десорбции U^BB, поэтому на рис. 6а они помечены одним номером) на закаленной равновесной поверхности твердого вещества А с диссоциацией при температуре вблизи плавления А для двух последних моделей: по модели 4 построена кривая 1 как общая средняя скорость сорбции Uⁱⁱ, и по модели 3 построены кривые 2, 3 и 4 как локальные скорости сорбции $U_{{qq}}^{{ii}}$ в монослоях q = 2, 3 и 4 соответственно. На рис. 6а, как и на рис. 5б, скорости адсорбции $U_{{qq}}^{{ii}}$ показаны на примере диссоциации на однотипных узлах.

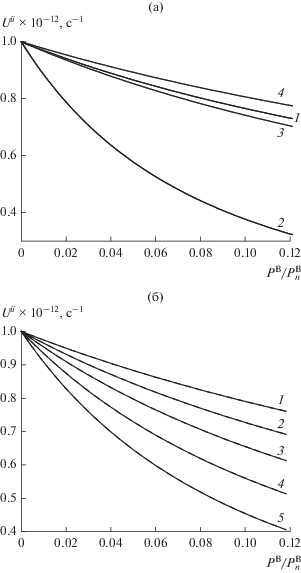
На рис. 6б представлены скорости адсорбции–десорбции газа В₂, U^VV/U^BB (все кривые адсорбции U^VV совпадают с соответствующими кривыми десорбции U^BB, поэтому на рис. 6б они помечены одним номером) на закаленной равновесной поверхности твердого вещества А с диссоциацией при температуре вблизи плавления А для модели 2 (узлы различаются по величине константы Генри): построены кривые 1–5 как локальные скорости адсорбции $U_{{m*m*}}^{{ii}}$ с числом частиц адсорбента в ближайшем окружении m* от 1 до 5 соответственно. Скорости адсорбции $U_{{m*m*}}^{{ii}}$ на рис. 6б показаны на примере диссоциации на однотипных узлах, т.е. в рамках модели 2 это означает, что диссоциация происходит на узлах с одним значением числа частиц А в ближайшем окружении m* (см. рис. 2в).

На рис. 6 видно, что все скорости адсорбции убывают с ростом давления P^B. Также получено, что все локальные значения адсорбции $U_{{m*m*}}^{{{\text{VV}}}}$ (рис. 6а) и $U_{{qq}}^{{ii}}$ и общее среднее значение U^VV (рис. 6а) численно совпадают с соответствующими значениями $U_{{m*m*}}^{{{\text{BB}}}},$ $U_{{qq}}^{{ii}}$ и U^BB процесса десорбции и образуют с ними общую кривую. Таким образом, для моделей 3 и 4 самосогласование уравнения изотермы адсорбции с уравнениями скоростей адсорбции с диссоциацией В₂ выполняется строго при любых температурах и давлениях вне зависимости от природы адсорбата и адсорбента как на равновесной, так и на закаленной равновесной поверхности.

Модель 2 не обеспечивает строгого выполнения самосогласования и может только приблизить значения скоростей адсорбции и десорбции с конечной точностью в зависимости от внешних параметров и природы компонентов в системе. Например, в данной работе, где адсорбция рассчитывалась при высоких температурах (выше критической температуры компонента В), получено совпадение скоростей $U_{{m*m*}}^{{{\text{VV}}}}$ и $U_{{m*m*}}^{{{\text{BB}}}}$ с точностью 99.98%. В работе [16], где адсорбцию считали при низких температурах (вблизи тройной точки В), скорости адсорбции и десорбции без диссоциации вследствие нарушения самосогласования расходились примерно в 2 раза! Причина рассогласования связана с видом функции неидеальности (формула (4в)), в которой появляется сумма по состоянию соседних узлов: для данного усреднения задается не весь кластер центрального узла одновременно, а по отдельности рассматриваются его пары с соседним узлом (что является грубым описанием). В результате получается сумма вкладов в функции неидеальности, что приводит к нарушению самосогласования.

ЭФФЕКТЫ КОРРЕЛЯЦИИ

Выше было отмечено, что пренебрежение эффектами корреляции взаимодействующих частиц приводит к нарушению условия самосогласования. В данной работе было проверено влияние учета эффектов корреляции взаимодействия частиц на условие самосогласованности в рассматриваемой задаче о хемосорбции компонента В₂ на равновесной шероховатой поверхности адсорбента. Для всех моделей пренебрежение эффектами корреляции взаимодействующих частиц приводит к нарушению условия самосогласования. Чтобы численно продемонстрировать эффект корреляции взаимодействия частиц, приведем данные расчета в ПСП (при тех же условиях в КХП самосогласование выполняется).

На рис. 7 представлены рассчитанные в приближении среднего поля скорости десорбции U^BB (1) и адсорбции U^VV (2) газа В₂ (здесь кривые адсорбции U^VV и десорбции U^BB расходятся, поэтому на рис. 7 им присвоены разные номера) на равновесной поверхности твердого вещества А с диссоциацией при температуре вблизи плавления вещества А для модели 4 с полным усреднением.

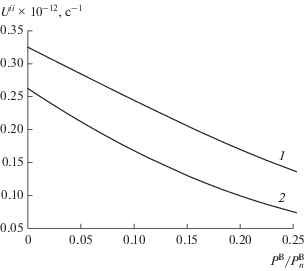
По сравнению с кривой 1 на рис. 5б, построенной в КХП, аналогичная кривая в ПСП лежит почти в 2 раза ниже, т.е. данная кривая в ПСП дает меньшие скорости сорбции. Также, согласно рис. 7, в приближении среднего поля условие самосогласованности выражений изотермы адсорбции и скоростей сорбции нарушается, так как наблюдаются расхождения до 45% (максимальные различия при ${{P_{{}}^{{\text{B}}}} \mathord{\left/ {\vphantom {{P_{{}}^{{\text{B}}}} {P_{n}^{{\text{B}}}}}} \right. \kern-0em} {P_{n}^{{\text{B}}}}}$ = 0.25) между скоростями адсорбции и десорбции.

ЗАКЛЮЧЕНИЕ

Анализ разных способов усреднений неоднородной поверхности показал, что нарушение условия самосогласования могут происходить в следующих случаях.

1. При использовании недостаточно точного усредненного описания адсорбционных центров кластера вокруг центрального узла на неоднородной поверхности (как в модели 2). В данной работе, где адсорбцию считали при высоких температурах, получено совпадение скоростей прямой и обратной реакции с точностью 99.98%, тогда как при низких температурах скорости мономолекулярной адсорбции и десорбции различались практически в 2 раза вследствие нарушения условия самосогласования [16].

2. При игнорировании эффектов корреляции. В случае неучета эффектов корреляции взаимодействия частиц при использовании приближения среднего поля нарушение самосогласования может приводить к различию в скоростях прямого и обратного направления реакции до 45%.

Установлено, что состояние неоднородной поверхности (равновесное или закаленное равновесное) не влияет на самосогласованность описания скоростей адсорбции и десорбции: модели 3 и 4 в рамках КХП всегда будут обеспечивать самосогласованность расчетов, тогда как модель 2 или использование ПСП приводят к нарушению самосогласованности.

Впервые проведенные исследования в данной работе и работе [16] показывают, что модели совместного учета неидеальности и неоднородности адсорбционной системы требуют контроля при их применении. Концепция самосогласования является принципиальной при выборе модели для описания экспериментальных данных. Например, для моделей 3 и 4 в КХП мы получаем строгое выполнение самосогласования уравнения изотермы адсорбции с уравнениями скоростей адсорбции при любых параметрах как без диссоциации В, так и с диссоциацией В₂, что указывает на универсальность построенных моделей. Применимость модели 2 имеет ограничения по температурному диапазону, и, используя ее, нужно учитывать степень рассогласования, к которой она приводит. Если точность используемых уравнений недостаточна по уровню описания самосогласования или по точности учета физико-химических факторов, то следует перейти на более детальные модели [3, 15].

Проведенный анализ имеет практическое значение, так как выбор модели для описания экспериментальных данных должен обеспечивать точное отражение физических факторов реакционной системы, а именно: неоднородность поверхности и взаимное влияние адсорбированных частиц друг на друга за счет латеральных взаимодействий. На практике обычно ищут компромисс между простой математической моделью для описания ее свойств и необходимыми требованиями при ее использовании (самосогласованность и точность учета физических факторов.)

ФИНАНСИРОВАНИЕ РАБОТЫ

Работа выполнена при поддержке РФФИ (код проекта № 18-03-00030а).