Кинетика и катализ, 2020, T. 61, № 1, стр. 144-148

Математическое моделирование влияния стефановского потока на процесс в зерне катализатора с использованием Mathcad

С. Г. Заварухин^a, b, *

^a ФГБУН Институт катализа им. Г.К. Борескова СО РАН
630090 Новосибирск, просп. Акад. Лаврентьева, 5, Россия

^b ФГБОУ ВО Новосибирский государственный технический университет
630073 Новосибирск, просп. К. Маркса, 20, Россия

^* E-mail: zsg@catalysis.ru

Поступила в редакцию 17.06.2019
После доработки 30.07.2019
Принята к публикации 11.09.2019

DOI: 10.31857/S0453881120010141

Полный текст (PDF)

Аннотация

Задача о влиянии стефановского потока в зерне катализатора для газофазной химической реакции m-го порядка A → nB была рассмотрена в [2]. Для решения применяли специальные численные методы. В настоящей работе предложен простой метод решения задачи о газофазной химической реакции первого порядка A → 2B с использованием программы Mathcad. В качестве иллюстрации метода рассчитаны профили безразмерных концентрации реагента и скорости газа стефановского потока при параметре Тиле ψ = 1 и мольной доле реагента А снаружи зерна θ = 1, зависимости степени использования катализатора от параметров ψ и θ в диапазоне ψ = 0.1–10 и θ = 0.1–1, а также зависимость отношения степени использования катализатора при θ = 1 к аналогичному параметру в отсутствие стефановского потока от параметра Тиле.

Ключевые слова: зерно катализатора, стефановский поток, реакция первого порядка, степень использования катализатора, Mathcad

ВВЕДЕНИЕ

Если в химическом процессе, протекающем в зерне катализатора, количество образующихся газов не совпадает с количеством газов, вступивших в реакцию, то в зерне возникает конвективный поток газа, называемый стефановским. При направлении потока от центра на периферию (реакция с увеличением объема газа) движение газа препятствует проникновению реагентов внутрь зерна и тем самым уменьшает степень использования катализатора. Для реакционных смесей с числом компонентов больше двух моделирование процесса осложняется зависимостью эффективных коэффициентов диффузии компонент от состава смеси [1]. Для бинарной смеси количество коэффициентов диффузии уменьшается до одного, причем коэффициент диффузии можно считать константой. Для реакции m-го порядка A → nB задача о влиянии стефановского потока на процесс была рассмотрена в [2] с использованием специальных численных методов. Для реакции первого порядка задача упрощается, но и в этом случае с математической точки зрения она является краевой задачей для нелинейной системы дифференциальных уравнений с особенностью в центре зерна. Решение такой задачи требует квалификации прикладного математика и навыков программирования. С появлением прикладных математических программ, в частности, программы Mathcad, которую изучают в вузах на младших курсах, многие достаточно сложные задачи стали доступны для решения студентам. Например, в [3] было предложено простое решение задачи о дезактивации катализатора внутри зерна с так называемым параллельным механизмом дезактивации. В настоящей работе с использованием Mathcad моделируется влияние стефановского потока на газофазный процесс, протекающий в зерне катализатора для реакции первого порядка A → 2B.

Примером реакции первого порядка A → 2B может служить реакция разложения метана на углерод и водород, на которой основан процесс получения нановолокон углерода из метана или метано-водородной смеси [4]. Если концентрация водорода в смеси невелика, то выражение для скорости реакции, например при использовании высокопроцентного никельсодержащего катализатора [5], принимает вид $w = k{{Р}_{{{\text{CH}}4}}}$, где k – константа скорости реакции, Р_CH4 – парциальное давление метана, и реакция может рассматриваться как необратимая реакция первого порядка.

ВЫВОД УРАВНЕНИЙ

Рассмотрим реакцию первого порядка A → 2B, протекающую в сферическом зерне катализатора. Скорость реакции w (моль м^–3 с^–1) имеет вид $w = kC,$ где k – константа скорости реакции (с^–1), C – концентрация реагента А (моль/м³). Радиус зерна равен b (м). Снаружи зерна поддерживается постоянная концентрация реагента C₀. Поступление реагента внутрь зерна обеспечивается за счет диффузии с эффективным коэффициентом диффузии D (м²/с).

Удельный поток реагента в зерне состоит из конвективной и диффузионной составляющих. В векторной форме выражение для удельного потока $\vec {j}$ (моль м^–2 с^–1) записывается в виде:

(1)

$\vec {j} = \vec {v}C - D\nabla C,$

где $\vec {v}$ – скорость газа (м/с), $\nabla $ – градиент.

В стационарном случае уравнения баланса по количеству реагента и объему газа имеют вид:

(2)

${\text{div}}\vec {j} = - w,$

(3)

${\text{div}}\vec {v} = w{{V}_{0}},$

где div – дивергенция, V₀ – объем одного моля идеального газа при температуре и давлении процесса (м³/моль).

Учитывая сферическую симметрию задачи, векторы $\vec {j}$ и $\vec {v}$ в сферической системе координат имеют ненулевые только радиальные компоненты, которые обозначим j и v соответственно. Выражение для j согласно (1) имеет вид:

(4)

$j = vC - D\frac{{dC}}{{dR}},$

где R – расстояние от центра зерна до выделенной точки (м).

Уравнение (2) в сферической системе координат имеет вид:

(5)

$\frac{1}{{{{R}^{2}}}}\frac{{\text{d}}}{{{\text{d}}R}}\left( {{{R}^{2}}j} \right) = - w,$

(6)

$ - \frac{{{\text{d}}j}}{{{\text{d}}R}} - \frac{{2j}}{R} = w.$

Преобразуя (6) с использованием (4), получим:

(7)

$D\left( {\frac{{{{{\text{d}}}^{2}}C}}{{{\text{d}}{{R}^{2}}}} + \frac{2}{R}\frac{{{\text{d}}C}}{{{\text{d}}R}}} \right) - v\frac{{{\text{d}}c}}{{{\text{d}}R}} - C\left( {\frac{{{\text{d}}v}}{{{\text{d}}R}} + \frac{{2v}}{R}} \right) = w.$

Уравнение (3) в сферической системе координат запишется в виде:

(8)

$\frac{1}{{{{R}^{2}}}}\frac{{\text{d}}}{{{\text{d}}R}}\left( {{{R}^{2}}v} \right) = w{{V}_{0}}.$

(9)

$\frac{{{\text{d}}v}}{{{\text{d}}R}} + \frac{{2v}}{R} = w{{V}_{0}}.$

C учетом (9) уравнение (7) преобразуется к виду:

(10)

$D\left( {\frac{{{{{\text{d}}}^{2}}C}}{{{\text{d}}{{R}^{2}}}} + \frac{2}{R}\frac{{{\text{d}}C}}{{{\text{d}}R}}} \right) - v\frac{{{\text{d}}C}}{{{\text{d}}R}} = w\left( {1 + {{V}_{0}}C} \right).$

Для реакции первого порядка система уравнений для C и v будет иметь вид:

(11)

$D\left( {\frac{{{{{\text{d}}}^{2}}C}}{{{\text{d}}{{R}^{2}}}} + \frac{2}{R}\frac{{{\text{d}}C}}{{{\text{d}}R}}} \right) - v\frac{{{\text{d}}C}}{{{\text{d}}R}} = kC\left( {1 + {{V}_{0}}C} \right),$

(12)

$\frac{{{\text{d}}v}}{{{\text{d}}R}} + \frac{{2v}}{R} = kC{{V}_{0}}.$

Граничные условия ставятся в центре и на границе зерна:

(13)

$\frac{{{\text{d}}C}}{{{\text{d}}R}}\left( 0 \right) = 0,\,\,\,\,v\left( 0 \right) = 0,\,\,\,\,C\left( b \right) = {{C}_{0}}.$

Запишем уравнения и граничные условия в безразмерном виде. Для этого введем безразмерные переменные:

(14)

$\xi = \frac{R}{b},\,\,\,\,y = \frac{C}{{{{C}_{0}}}},~\,\,\,\,u = \frac{v}{{kb{{V}_{0}}{{C}_{0}}}}.$

В безразмерном виде уравнения и граничные условия примут вид

(15)

$\frac{{{{{\text{d}}}^{2}}y}}{{{\text{d}}{{\xi }^{2}}}} + \frac{2}{\xi }\frac{{{\text{d}}y}}{{{\text{d}}\xi }} - {\theta }{{\psi }^{2}}u\frac{{{\text{d}}y}}{{{\text{d}}\xi }} = {{\psi }^{2}}y\left( {1 + {\theta }y} \right),$

(16)

$\frac{{{\text{d}}u}}{{{\text{d}}\xi }} + \frac{{2u}}{\xi } = y,$

(17)

$\frac{{{\text{d}}y}}{{{\text{d}}\xi }}\left( 0 \right) = 0,\,\,\,\,u\left( 0 \right) = 0,\,\,\,\,y\left( 1 \right) = 1,$

где ψ – параметр Тиле, $\psi = b\sqrt {\frac{k}{D}} ;$ θ – безразмерный параметр, $\theta = {{C}_{0}}{{V}_{0}},$ равный мольной доле реагента А на внешней границе зерна.

Степень использования катализатора η после решения системы уравнений рассчитывается по формуле

(18)

${\eta } = 3\int\limits_0^1 y \left( \xi \right){{\xi }^{2}}{\text{d}}\xi .$

МЕТОД РЕШЕНИЯ

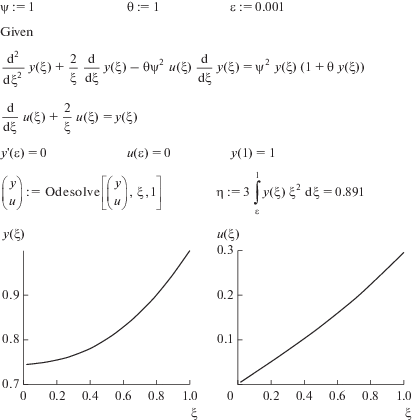
Систему уравнений (15), (16) с граничными условиями (17) решали с помощью функции Given-Odesolve программы Mathcad. Особенность при ξ = 0 обходили путем сноса граничного условия при ξ = 0 в точку ξ = ε, где ε – малая величина, принятая равной 0.001.

Программа в Mathcad, позволяющая рассчитывать профили y(ξ) и u(ξ) и степень использования катализатора по заданным параметрам ψ и θ, приведена на рис. 1. Можно заметить, что программа вместе с графиками по объему занимает не более половины страницы.

Рис. 1.

Программа Mathcad для расчета профилей безразмерных концентрации реагента и скорости газа стефановского потока и степени использования катализатора в зависимости от параметров ψ и θ.

РЕЗУЛЬТАТЫ РАСЧЕТА

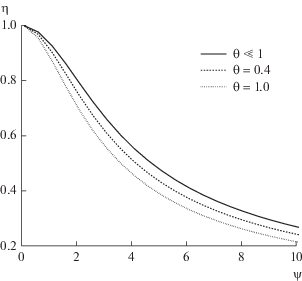
На рис. 2 показана зависимость степени использования катализатора от параметра Тиле при различных значениях параметра θ.

Рис. 2.

Зависимость степени использования катализатора от параметра Тиле при различных значениях параметра θ.

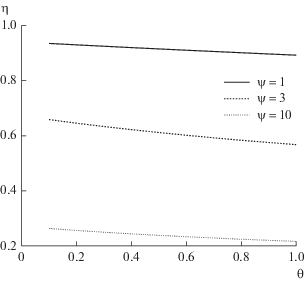
На рис. 3 представлена зависимость степени использования катализатора от параметра θ при различных параметрах Тиле.

Рис. 3.

Зависимость степени использования катализатора от параметра θ при различных значениях параметра Тиле.

На рис. 4 приведено отношение степени использования катализатора при θ = 1 к степени использования катализатора без стефановского потока (θ $ \ll $ 1) от параметра Тиле. Под условием θ $ \ll $ 1 подразумевается предельный случай θ → 0, для которого уравнение (15) принимает вид:

(19)

$\frac{{{{{\text{d}}}^{2}}y}}{{{\text{d}}{{\xi }^{2}}}} + \frac{2}{\xi }\frac{{{\text{d}}y}}{{{\text{d}}\xi }} = {{\psi }^{2}}y,$

и степень использования катализатора без стефановского потока η0 рассчитывается по известной формуле [6]

(20)

$\eta 0 = \frac{3}{\psi }\left( {\frac{1}{{th\psi }} - \frac{1}{\psi }} \right).$

Рис. 4.

Зависимость отношения степени использования катализатора при θ = 1 к степени использования катализатора без стефановского потока от параметра Тиле.

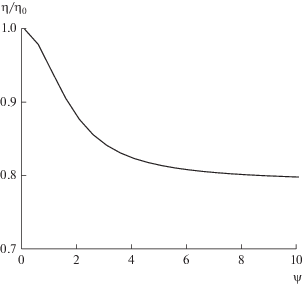
Расчеты показывают, что при ψ < 10 степень использования зерна уменьшается не более чем на 20%.

ЗАКЛЮЧЕНИЕ

В настоящей работе предложен простой метод решения задачи о газофазной химической реакции первого порядка A → 2B, протекающей в зерне катализатора, для которой характерно наличие стефановского потока. По сравнению с работой [2], в которой применяли специальные численные методы, предлагаемый метод основан на использовании функций прикладной математической программы Mathcad. В качестве иллюстрации метода рассчитаны профили безразмерных концентрации реагента и скорости газа стефановского потока при параметре Тиле ψ = 1 и мольной доле реагента А снаружи зерна θ = 1, зависимости степени использования катализатора от параметров ψ и θ в диапазоне ψ = 0.1–10 и θ = 0.1–1, а также отношения степени использования катализатора при θ = 1 к аналогичному параметру без стефановского потока.

Список литературы

Малиновская О.А., Бесков И.С., Слинько М.Г. Моделирование каталитических процессов на пористых зернах. Новосибирск: Наука, 1975. С. 266.
Weekman V.W., Gorring R.L. // J. Catal. 1965. V. 4. P. 260.
Заварухин С.Г. // Кинетика и катализ. 2017. Т. 58. № 6. С. 804.
Baker R.T.K., Harris P.S. // Chem. Phys. Carbon. 1978. V. 14. P. 83.
Zavarukhin S.G., Kuvshinov G.G. // Appl. Catal. A: General. 2004. V. 272. № 1–2. P. 219.
Боресков Г.К. Гетерогенный катализ. Москва: Наука, 1988. С. 304.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Кинетика и катализ

Архивы выпусков Информация о журнале Отправить рукопись в журнал